Диффузия

Диффузия (от dis — раз, fundere — лить, diffundere — разливать). Диффузией называется процесс смешения двух или нескольких соприкасающихся друг с другом газов или жидкостей, причем в жидкостях диффузия может происходить только тогда, когда данные жидкости вообще могут смешиваться друг с другом. Примером не смешивающихся жидкостей может служить ртуть и вода; наоборот, водный раствор какой-нибудь соли может смешиваться с растворителем (водой) в любой пропорции. В промежутке между этими группами жидкостей стоят такие, которые хотя и могут смешиваться, но только до известного предела; так, например, вода может смешиваться с хлороформом, но только до тех пор, пока количество воды, смешавшейся с хлороформом, не достигнет некоторой, вполне определенной величины; если две такие жидкости соприкасаются, то процесс смешения—диффузии происходит сам собой, но только до указанного предела. Если две жидкости смешиваются в любых пропорциях, то процесс диффузии продолжается до тех пор, пока не получится повсюду однородная смесь; в газах диффузия происходит всегда по этому типу. Диффузия  происходит и в твердых телах, хотя и чрезвычайно медленно; так, если покрыть толстую свинцовую пластинку слоем золота, то через некоторое время золото проникает в самую толщу свинца. Явление диффузии жидкостей особенно наглядно, если одна из жидкостей окрашена, например, раствор медного купороса в воде и вода. Для изучения самого процесса диффузии существует несколько методов.

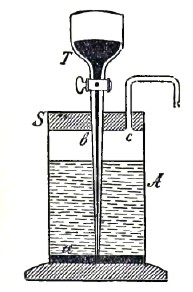
Рис.1

а) На дно стакана А (рис. 1) наливают небольшое количество ртути для того, чтобы получить гладкую поверхность; поверх ртути наливается чистый растворитель (в большинстве случаев вода); при помощи воронки Т осторожно приливают раствор какой-нибудь соли, диффузию которой желают изучить: более тяжелый раствор располагается ровным слоем между ртутью и водой. В таком виде прибор оставляют стоять в течение известного промежутка времени, предохраняя его от сотрясений, после чего, осторожно приливая ртуть на дно сосуда через воронку Т, вытесняют через трубку с верхний слой жидкости и определяют в ней количество соли. Таким путем можно найти, какое количество соли проходит через слой растворителя за известный промежуток времени. Точное исследование явления требует высшего математического анализа; в основе этого математического анализа явления диффузии лежит следующий, установленный опытом факт. Количество перенесенного в единицу времени вещества Q пропорционально площади сечения сосуда q, обратно пропорционально длине l и прямо пропорционально убыли концентрации с₂—с₁ растворенного вещества в начале и конце столба жидкости l. Следовательно, Q = k [(с2-с1)/l]q; здесь k коэффициент диффузии. Он имеет следующий смысл: положив с2—с1 = l, q=1 и l=1, мы получаем Q=k, следовательно, коэффициент диффузии показывает, какое количество вещества переносится в единицу времени через единицу площади между двумя слоями, отстоящими друг от друга на расстоянии 1 cm, при разности концентрации = 1.

b) Для изучения распределения концентраций лордом Кельвином был предложен метод поплавков; стеклянные шарики наполняются водой или раствором, причем в них оставляют большее или меньшее количество воздуха и запаивают. Таким образом, получаются поплавки различного веса; поплавки остаются в том слое, где вес вытесненного раствора равен весу поплавка; определив предварительно концентрацию, соответствующую каждому из поплавков, мы можем, отметив их и пустив в диффундирующую смесь, найти распределение концентрации.

с) Так как растворы имеют показатель преломления (см. свет), зависящий от концентрации, то воспроизводя явление диффузии в призматическом сосуде, можно определять изменение концентрации по величине отклонения пучка света, прошедшего через призму на различных уровнях.

d) Диффузия веществ, вращающих плоскость поляризации (см. поляризация света, сахариметрия), можно также изучать оптически. Диффузия  может происходить через пористые перегородки, причем некоторые из них, т. н. полупроницаемые, пропускают растворитель и не пропускают растворенного тела. Об этих явлениях см. осмос. Указанная в а) математическая теория, представляющая обобщение опыта, интересна тем, что она приводит к уравнениям, формально тождественным с уравнениями распространения тепла и электричества, но самого механизма явления диффузии она не касается. Дальнейший шаг в этом направлении сделала молекулярно-кинетическая теория; эта теория детально разработана только для газообразного состояния материи, хотя в последнее время сделаны крупные шаги и в кинетической теории жидкостей. Самое представление о механизме диффузии с молекулярно-кинетической точки зрения можно наглядно иллюстрировать следующей картиной: представим себе половину биллиардного стола занятой белыми шарами, другую — черными и предположим, что все шары двигаются в хаотическом беспорядке, — рано или поздно шары перемешаются; взаимные столкновения замедляют этот процесс диффузии, — обстоятельство, на которое обратил внимание Клаузиус в ответ на возражения против кинетической теории, в которой указывалось, что медленность процесса диффузии противоречит тем большим скоростям поступательного движения, какие мы должны приписать молекулам согласно кинетической теории. Построенная на этих основах математическая теория устанавливает связь между диффузией и целым рядом других явлений, как, например, передача количества движения (явления трения) и передача тепла (явления теплопроводности), и эта связь многократно была проверена на опыте. Очень легко наблюдать явление диффузии газов через пористые перегородки; этот случай легко объясняется кинетической теорией, в особенности в том случае, когда поры настолько малы, что при прохождении газа через отверстия мы можем отвлечься от взаимных столкновений молекул; тогда скорость диффузии будет пропорциональна скорости движения молекул. При одинаковой температуре средняя кинетическая энергия молекул любого газа одна и та же: m₁u₁²/2 = m₂u₂²/2, откуда скорости двух газов будут находиться в обратном отношении квадратных корней из молекулярных весов: u₁/u₂ = √m₂/m₁

Этот закон был найден из опыта Грэамом. В настоящее время кинетическая теория, благодаря целому ряду теоретических исследований, распространена и на растворы, как молекулярные (растворы в собственном смысле этого слова), так и на коллоидные, а также и на эмульсии. Предпринятые на основании этих исследований экспериментальные работы привели к согласным с теорией результатам и позволили, на основании измерения коэффициента диффузии, определить совершенно новым и независимым от прежних методов путем основную в молекулярной теории величину: число молекул в грамм-молекуле какого угодно вещества.

Литература: О. Хвольсон, «Курс физики»; О. Е. Meyer, «Die kinetische Theorie der Gase» (1899); Byk, «Einführung in die kinetische Theorie der Gase» (1910); Перрен, «Броуновское движение и молекулы». Новые идеи в физике. Сборник № 1, 911. Th. Svedberg, «Die Existenz der Molekülle» (1912).

А. Тимирязев.