Электричество. Глава I. Электростатика

Электричество. Глава I. Электростатика. § 1. Основные факты и понятия (электрический заряд, напряженность поля, потенциал). Понятие «электричество» связано с представлением об особого рода силах, которые появляются между двумя телами, если привести их путем надлежащего воздействия, например, путем трения друг о друга, в некоторое отличное от обычного «наэлектризованное» состояние. При этом под электричеством понимается то свойство обоих тел, от которого зависят эти силы.

Классические исследования Кулона (конец XVIII века) показали, что это свойство, называемое обычно электрическим зарядом, аналогично массе тел, то есть тому свойству, от которого зависит их взаимное притяжение по закону Ньютона (см. тяготение). Сходство между зарядом и массой заключается в том, что соответствующие силы — электрические и гравитационные — одинаковым образом зависят от положения взаимодействующих тел; если размеры последних малы в сравнении с расстоянием между ними, то есть если их можно трактовать как «материальные точки» или как «точечные заряды», то в обоих случаях сила взаимодействия с увеличением расстояния убывает обратно пропорционально его квадрату, причем направлена она вдоль прямой, соединяющей соответствующие частицы. Что касается различий между зарядом и массой, то в основе своей они сводятся к существованию двух родов электрических зарядов с противоположными свойствами, причем заряды разного рода взаимно притягиваются, а заряды одного и того же рода взаимно отталкиваются. Таким образом, ньютоновское притяжение вполне аналогично лишь взаимодействию разнородных электрических зарядов. Заметим, что электрические силы могут достигать (и обычно достигают) несравненно большей величины, чем гравитационные силы, и потому гораздо отчетливее обнаруживаются и легче измеряются, нежели последние.

Подобно тому, как масса (см.) тела может быть определена по величине силы притяжения, которую оно оказывает на какое-нибудь другое тело (или испытывает со стороны последнего), — электрический заряд тела может быть определен по силе притяжения или отталкивания, производимого им на электрический заряд другого тела. Считая заряд пропорциональным оказываемой или испытываемой им электрической силе, можно выразить закон Кулона, характеризующий силу взаимодействия f_AB между двумя наэлектризованными телами А и В, в форме, совершенно аналогичной обычной формулировке закона Ньютона:

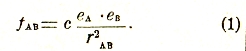
Здесь е_А и е_В обозначают заряды обоих тел, r_AB — расстояние между ними (которое предполагается весьма большим в сравнении с их линейными размерами), а с — коэффициент пропорциональности, зависящий от выбора единиц. Обычно полагают с = 1. При этом единица электрического заряда определяется как такой заряд, который на равный ему заряд, находящийся на единице расстояния, действует с единицей силы. Далее, зарядам противоположного рода приписываются противоположные знаки (+, -); при этом условии для силы отталкивания между двумя однородными («одноименными») зарядами по формуле (1) получается положительный знак, а для силы притяжения между разнородными (разноименными) зарядами — отрицательный знак.

Величина

  

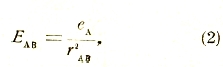
равная силе, производимой зарядом тела А на единицу положительного заряда, помещенную в точке В, называется электрической напряженностью¹) в точке В. Сила f_AB, действующая на тело В, получается при этом умножением напряженности Е_AB на заряд е_B. Это соотношение между силой и напряженностью сохраняется для любого электрического поля, то есть пространства, в котором действуют электрические силы, зависящие от любого распределения электрических зарядов.

¹) Или напряженностью электрического поля.

Рассматривая силу, действующую в точке Р на заряд е, как направленную величину, то есть как вектор , мы получаем для напряженности электрического поля в этой точке также векториальную величину , связанную с силой соотношением

В случае положительного заряда (е > 0) сила имеет направление, совпадающее с напряженностью, а в случае отрицательного заряда (е < 0) — ему противоположное. Это значит, что в одном и том же месте заряды разного рода (противоположного знака) испытывают противоположно направленные силы.

Рассматриваемые нами электрические силы называются электростатическими, так как они зависят — помимо величины соответствующих зарядов — исключительно от их (относительного) положения. Закон Кулона относится лишь к тому случаю, когда эти положения остаются неизменными или меняются очень медленно. Мы увидим ниже, что в случае движущихся зарядов к кулоновым электростатическим силам присоединяются силы электрокинетические, зависящие не только от положения зарядов, но также от их скорости и ускорения. Далее мы увидим, что все эти силы передаются от одной частицы к другой не мгновенно, а с конечной скоростью, равной скорости света. Последнее обстоятельство не играет роли в том случае, если рассматриваемые частицы неподвижны или движутся достаточно медленно.

В пределах применимости закона Кулона электрические силы, подобно силам тяготения, обладают консервативным характером. Последний выражается в существовании потенциальной энергии, то есть определенной функции относительных положений (расстояний) всех рассматриваемых частиц, уменьшением которой определяется работа, совершаемая силами взаимодействия при переходе от одного расположения к другому (см. XXXIV, 358/59). Существование подобной функции означает независимость этой работы от промежуточных расположений или, как говорится, от пути перехода.

В простейшем случае двух частиц с зарядами е_А и е_В потенциальная энергия выражается формулой

при условии, чтобы она обращалась в нуль, когда частицы находятся на бесконечно большом расстоянии друг от друга. В общем случае любого числа наэлектризованных частиц потенциальная энергия образуемой ими системы сводится к сумме выражений (4) для каждой пары частиц, взятой в отдельности. Потенциальная энергия одной частицы по отношению к остальным может быть определена как сумма выражений (4) для всех комбинаций данной частицы с остальными. Отсюда следует, что потенциальная энергия системы нескольких частиц равна половине суммы потенциальных энергий каждой из них по отношению к остальным (ср., например, случай двух частиц).

Потенциальная энергия U наэлектризованной частицы в данном электрическом поле может быть представлена, подобно действующей на нее силе , в виде произведения ее заряда е на некоторый множитель V по формуле

Этот множитель (соответствующий напряженности поля ) представляет собой потенциальную энергию единицы положительного заряда, помещенной в рассматриваемой точке, и называется электрическим потенциалом. В случае электрического поля, создаваемого точечным зарядом e_А, потенциал в точке В определяется формулой

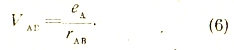
Работа, совершаемая силой , действующей на заряд е при перемещении его на бесконечно малый отрезок Δs, равна произведению fs · Δs, где f_S обозначает проекцию вектора на направление Δs. Приравнивая эту работу уменьшению потенциальной энергии U, получаем

где U₁ и U₂ - значения U в начале и в конце отрезка Δs. Это равенство по разделении на е превращается в соотношение между электрической напряженностью и потенциалом:

Оно выражает то обстоятельство, что слагающая электрической напряженности в каком-либо направлении равна быстроте падения потенциала в этом направлении. Направление вектора

8 совпадает, таким образом, с направлением наиболее быстрого падения V, причем величина Е равна быстроте этого падения (определяемого как отношение разности потенциалов на концах соответствующего отрезка к длине последнего). Вектор называется при этом градиентом потенциала V.

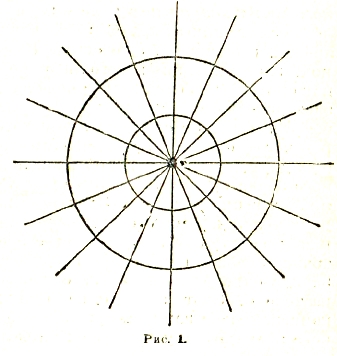
Для наглядного изображения электрического поля служат так называемые силовые линии и эквипотенциальные поверхности. Первые проводятся таким образом, чтобы направление их в каждой точке совпадало с направлением в этой точке и чтобы, далее, густота их вблизи нее была пропорциональна величине Е. При этом «густота» определяется числом линий, пересекающих единицу перпендикулярной к ним поверхности. Подобные поверхности, перпендикулярные к силовым линиям, характеризуются определенными постоянными значениями потенциала и потому называются эквипотенциальными. В случае точечного заряда, силовые линии образуют равномерно расходящийся во все стороны пучок лучей (густота которого обратно пропорциональна квадрату расстояния), а эквипотенциальными поверхностями являются сферы с общим центром в этом заряде.

§ 2. Действие наэлектризованных тел па нейтральные; электростатическая индукция и электрическая поляризация; проводники и диэлектрики. В предыдущем параграфе мы изложили формальные основы учения об электростатических явлениях, введя в качестве основного понятия понятие об электрическом заряде. Переходя к рассмотрению конкретного физического содержания этих явлений, мы должны, прежде всего, ответить на следующий вопрос: почему электрический заряд обыкновенных тел, в противоположность их массе, представляет собой свойство непостоянное, в обычных условиях совершенно исчезающее и появляющееся лишь при определенных воздействиях на эти тела (например, при трении друг о друга)?

Ответ на этот вопрос непосредственно связан с двойственной природой электричества, с существованием электрических зарядов двух противоположных родов, или «знаков». Мы можем себе представить, что электрические заряды каждого рода подчиняются тому же «закону сохранения», как и масса, и что, далее, алгебраическая сумма положительных и отрицательных зарядов в каждом теле при обычных условиях равна нулю, то есть, другими словами, что положительные и отрицательные заряды присутствуют в каждом не наэлектризованном, или нейтральном теле в эквивалентных количествах. С этой точки зрения, выдвинутой еще самим Кулоном, электризация какого-либо тела или системы тел означает не появление электрического заряда, которого раньше вовсе не было, но обнаружение некоторой части одного из двух маскировавших друг друга зарядов противоположного знака путем частичного разделения их в пространстве. Электризация двух тел А и В при соприкосновении или трении обусловливается с этой точки зрения переходом некоторого заряда определенного знака с тела А на тело В. Этот заряд е, не будучи компенсирован зарядом противоположного знака, обнаруживается на теле В в виде заряда е_В = е, а на теле А в виде оставшегося некомпенсированным заряда противоположного знака е_А = -е. Практически существенный вопрос о том, какой из двух противоположных зарядов считать положительным и какой отрицательным, не имеет принципиального значения. По первоначальному определению принято считать отрицательным тот заряд, который появляется на стекле при трении его об амальгамированную кожу. Наоборот, вопрос о том, как велики электрические резервы, скрывающиеся в каждом теле, то есть как велики запасы положительного и отрицательного электричества, которые в нем компенсируются, имеет чрезвычайно большое принципиальное значение, но не играет никакой практической роли. Практически эти запасы можно считать неисчерпаемыми, то есть бесконечными.

Наличие противоположных электрических зарядов в любом нейтральном теле легко обнаруживается благодаря воздействию, которое оно испытывает со стороны какого-нибудь наэлектризованного тела. Это воздействие заключается во взаимном притяжении (например, притяжении бузиновых шариков наэлектризованной стеклянной палочкой), быстро ослабевающем с увеличением расстояния — значительно быстрее, нежели притяжение между двумя противоположно наэлектризованными телами. Причина рассматриваемого притяжения заключается в следующем. Под влиянием заряженного тела А заряды противоположного знака, скрывающиеся в нейтральном теле В, испытывают притяжение, а заряды того же знака — отталкивание. Результатом этих сил является некоторое приближение первых к телу А и некоторое удаление вторых, чем в свою очередь обусловливается некоторое увеличение сил притяжения и некоторое ослабление сил отталкивания. А так как при первоначальном равномерном распределении зарядов обоих знаков по всему объему тела В эти силы взаимно уравновешивались, то теперь при видоизмененном распределении, вызванном или, как говорится, «индуцированном» зарядом А, силы притяжения получают некоторый перевес над силами отталкивания. Этот перевес и обнаруживается нами как сила притяжения между наэлектризованным телом А и нейтральным телом В.

Указанное явление носит название электростатической индукции, или «электризации через влияние». Однако, это обозначение имеет смысл лишь в том случае, когда, отделив друг от друга две половины тела В — ближайшую к А (В₁) и более отдаленную (В₂) — мы обнаруживаем на каждой из них электрические заряды. Само собой разумеется, что эти заряды равны друг другу по величине и противоположны по знаку, причем заряд ближайшей к А половины В противоположен по знаку заряду А, а заряд другой половины совпадает по знаку с А (рис. 2).

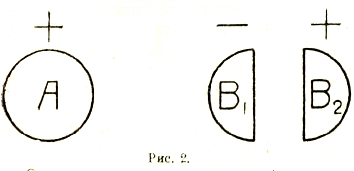
Однако, во многих случаях обе половины тела В, по отделении их друг от друга, остаются нейтральными, испытывая каждая в отдельности со стороны А притяжение того же рода (хотя и меньшей силы), как и все тело В. В подобных случаях состояние, в которое приводится тело В электрическим полем, исходящим от А, называется электрической поляризацией. Такую же «поляризацию» (вместо электризации) мы находим и в каждой из половинок тела В по отделении их друг от друга. В случае поляризации, так же как и в случае электризации через влияние, мы имеем дело со сдвигом противоположных зарядов в противоположные стороны. Разница между ними заключается, очевидно, в том, что во втором случае в теле имеются заряды, могущие свободно перемещаться по всему его объему, тогда как в первом случае заряды противоположного знака остаются прочно связанными друг с другом внутри очень маленьких элементов объема тела. Тела, содержащие свободно перемещающиеся или просто «свободные» заряды, называются проводниками; сюда относятся, прежде всего, металлы, а также электролиты (водные растворы солей, кислот и щелочей). Остальные тела, содержащие одни только связанные заряды, называются изоляторами, или диэлектриками. Само собой разумеется, что наличие в теле свободных зарядов отнюдь не исключает наличия в нем связанных¹).

§ 3. Электрическая природа сил молекулярного сцепления и химического сродства: ионы и атомы электричества. Мельчайшими частицами материальных тел обычно считаются молекулы и атомы. Описанные выше электрические свойства материальных тел естественно наводят на мысль о том, что эти частицы, и в частности атомы, состоят из еще более мелких частиц, обладающих электрическими зарядами противоположного знака, которые являются столь же неизменным и неотъемлемым их свойством, как и масса. Это представление о существовании субатомных наэлектризованных частиц, из которых слагаются обыкновенные нейтральные атомы, образует сущность современной электрической теории материи (см. материя и электронная теория). Оно дает возможность свести междуатомные и междумолекулярные силы, то есть в сущности все силы природы, кроме сил ньютоновского тяготения, — к электрическим силам, с которыми действуют друг на друга по закону Кулона заряженные элементарные частицы, из которых состоят атомы. Так, например, силы молекулярного сцепления (см. XLI, ч. 5, 607/09), то есть силы взаимного притяжения, которые оказывают друг на друга нейтральные атомы и молекулы при очень малом расстоянии между ними и которыми обусловливается существование твердых и жидких тел, могут быть в принципе объяснены по такой же схеме, которая была применена выше к объяснению притяжения между наэлектризованным и нейтральным телом.

Предположим, например, что рассмотренное выше тело А представляет собой нейтральную молекулу — так же, как и тело В.

¹) К таким телам принадлежат проводники и так называемые полупроводники.

Поскольку частица А состоит из нескольких наэлектризованных частиц, вокруг нее должно иметься электрическое поле, практически исчезающее на таких расстояниях, которые велики по сравнению с размерами А, то есть с расстояниями между образующими ее заряженными частицами¹), но более или менее значительное — сравнимое с полем каждого из этих зарядов в отдельности — на расстояниях того же порядка величины, то есть близких к молекулярным размерам. Находясь в этом поле, молекула В может поляризоваться совершенно таким же образом, как и в поле заряженного тела. Мы предполагаем при этом, что заряженные частицы, из которых слагается В, не могут оторваться друг от друга, но перемещаются таким образом, чтобы притягиваемые частицы приблизились к А, а отталкиваемые, наоборот, удалились.

Наряду, однако, с подобной поляризацией, при которой молекула В ведет себя как маленькое диэлектрическое тело, приближение притягиваемых и удаление отталкиваемых частиц может осуществляться также, вообще говоря, путем надлежащей ориентации молекулы В по отношению к А (подобно тому, как это происходит в случае двух магнитов, см. магнетизм). Само собой разумеется, что аналогичные изменения в строении и ориентации молекулы А вызываются электрическим полем молекулы В. В результате подобной взаимной поляризации и взаимной ориентации, между обеими молекулами появляется сила притяжения, чрезвычайно быстро убывающая с увеличением расстояния (примерно, обратно пропорционально седьмой степени расстояния), но при малых расстояниях могущая достигать очень большой величины²).

Аналогичными соображениями объясняется в принципе происхождение сил химического сродства между атомами (см. XLV, ч. 2, 346/47; ср. элементы). В некоторых случаях, однако, электрическая природа этих сил является непосредственно очевидной.

¹) При этом все частицы действуют приблизительно так, как если бы они были сконцентрированы в одной точке с полным зарядом = 0.

²) Эти представления о природе сил сцепления были впервые развиты Кезомом (1913) и Дебаем (1920), а в последнее время, на основе квантовой механики, Лондоном (1931).

Это относится к веществам, образующим при растворении в воде так называемые электролиты. В то время, как в безводном состоянии эти вещества (соли, кислоты, щелочи) являются изоляторами, водные растворы их являются проводниками, то есть содержат электрические заряды, могущие свободно перемещаться по всему объему раствора. Ближайшее исследование показывает, что эти заряды связаны с отдельными атомами или группами атомов, из которых состоят рассматриваемые молекулы и на которые они могут распадаться при химических процессах. Подобные заряженные атомы или группы атомов называются ионами (см. XXII, 659 сл.), а самый процесс распада нейтральных молекул на (противоположно заряженные) ионы называется ионизацией, или электролитической диссоциацией (см. электрохимия).

То обстоятельство, что в водном растворе молекула распадается на ионы, свидетельствует о том, что и в нераспавшемся состоянии она образована соединением противоположных ионов, а не нейтральных атомов. Отсюда ясно, что в данном случае химические силы, по крайней мере, отчасти, сводятся к электрическому притяжению между противоположными ионами.

Вещества, молекулы которых образованы не нейтральными атомами, но ионами, называются ионными, или гетерполярными. Одним из простейших их представителей является поваренная соль, молекула которой состоит из положительного иона натрия (Na⁺) и отрицательного иона хлора (Сl^-), или соляная кислота Н⁺Сl^-, где Н⁺ обозначает положительный ион водорода. В сухом состоянии эти вещества не проявляют своих специфических свойств, приобретая их лишь в водном растворе. Роль воды заключается при этом в ослаблении связи между противоположными ионами (благодаря их притяжению к молекулам воды). В результате химическое разложение, которое при отсутствии воды требовало бы очень высокой температуры, осуществляется и при обычных температурах.

Представление об ионной структуре молекул весьма широкого класса веществ и о чисто электрической природе сил химического сродства между образующими их ионами в связи с учением о химической валентности приводит неизбежным образом к представлению об атомизме электрического заряда. Валентность каждого атома (или группы атомов) определяется в химии как число атомов водорода, которые он (или она) может замещать или удерживать в химическом соединении (см. элементы). При этом имеются в виду не нейтральные атомы, но ионы, и в частности ионы водорода. Считая, что последние имеют всегда один и тот же положительный заряд (+ε), мы оказываемся вынужденными приписать всем другим ионам заряды равные или кратные этому элементарному заряду со знаком + для положительных ионов (замещающих водород) и знаком - для ионов отрицательных (удерживающих водород). В самом деле, если, например, в молекуле серной кислоты Н₂SО₄ ион Н имеет тот же заряд, что и в молекуле соляной кислоты НСl, то это значит — в виду нейтральности обеих молекул, — что ион Сl имеет отрицательный заряд той же величины (-ε), а ион SO₄ отрицательный заряд вдвое большей величины. Вообще поскольку валентность различных атомов (или атомных групп) по отношению к водороду выражается небольшими целыми числами (k), электрический заряд этих атомов (или групп) должен составить небольшое целое кратное этого или противоположного заряда, то есть должен равняться ±kε (k = 1; 2...).

Другими словами — электрический заряд любой материальной частицы может составлять лишь целое число элементарных электрических зарядов, или «атомов электричества» ±ε. Подобные «атомы электричества» следует при этом представлять себе не как нечто отдельное от материи, а как минимальные электрические заряды простейших субатомных ее частиц.

Вопрос только в том, что именно представляют собой эти частицы?

§ 4. Протоны и электроны. Ответ, к которому пришла современная физика, в высшей степени прост и сводится к следующему. Простейшими положительными (то есть положительно заряженными) частицами материи являются положительные ионы самого легкого химического элемента — водорода, так называемые протоны. Что касается простейших отрицательных (то есть отрицательно заряженных) частиц материи, то таковыми мы можем считать их партнеров, образующих в соединении с ними нейтральные водородные атомы. Эти отрицательные частицы, называются электронами. Всякий более сложный атом представляет собой систему, образованную соединением нескольких протонов и такого же числа электронов. То обстоятельство, что электроны не обнаруживаются в виде отрицательных ионов водорода, объясняется чрезвычайной малостью их массы по сравнению с массой протонов в связи со способностью их связываться с другими более тяжелыми частицами, как нейтральными (атомы, молекулы), так и положительно заряженными. При этом положительные ионы образуются из нейтральных атомов путем отделения одного или нескольких электронов, а отрицательные — путем присоединения одного или нескольких электронов. Число потерянных или захваченных электронов и определяет валентность иона. Протоны, никогда не переходят от одного атома, к другому. В каждом атоме они образуют вместе с частью электронов центральный сгусток — так называемое положительное ядро, являющееся средоточением практически всей массы атома. Остальные электроны образуют «оболочку» атома, вращаясь вокруг ядра подобно тому, как планеты вращаются вокруг солнца (см. электронная теория).

Не останавливаясь на дальнейшем обосновании или развитии этой «ядерной» теории строения атомов (предложенной в 1911 году Рэзерфордом), мы приведем лишь данные относительно заряда протонов и электронов¹). Заряд, этот ±ε равен 4,77·10^-10 абсолютных электростатических единиц. Чтобы составить себе представление об этой цифре, заметим, что в одном грамме водорода содержатся 6,06·10²³ атомов, то есть, следовательно, 6,06·10²³ протонов и столько же электронов.

¹) Эти данные могут быть получены путем изменения количества электричества, переносимого в электролитах при прохождении электрического тока определенным весовым количеством материи.

Таким образом, запас положительного и отрицательного электричества в одном грамме водорода, а, следовательно, и всякого другого вещества (поскольку все атомы состоят из протонов и электронов) выражается приблизительно в тех же единицах числом

Это значит, что если бы мы могли сконцентрировать в одной точке (А) весь положительный, а в другой (В) весь отрицательный заряд, таящийся в 1 грамме материи, то на расстоянии r сантиметров эти заряды притягивали бы друг друга с силой

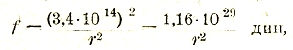
или, так как 1 000 дин составляет примерно вес одного грамма,

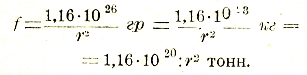
Полагая здесь r = 12 000 км, что составляет приблизительно диаметр земного шара, или r = 1,2·10⁷ см, получаем

Таким образом, если бы нам удалось отделить друг от друга противоположные заряды, содержащиеся в 1 грамме материи, и поместить их на противоположных полюсах земного шара, то на этом колоссальном расстоянии они притягивали бы друг друга с силой около 1 миллиона тонн. Этот результат дает нам некоторое представление о необычайной величине скрытых в материи электрических резервов, а также об отношении между электрическими силами и силами гравитационными. Последние, как мы видим, совершенно исчезают по сравнению с первыми. Однако, именно благодаря своей необычайной величине электрические силы непосредственно не обнаруживаются: они прочно удерживают протоны и электроны в отдельных атомах и молекулах, образуя таким образом нейтральные частицы, которые действуют друг на друга лишь на чрезвычайно маленьких расстояниях.

Те электрические заряды, которые мы сообщаем разным телам путем трения друг о друга или какими-нибудь другими способами и которые порождают непосредственно наблюдаемые электрические силы, ничтожно малы по сравнению с зарядами, которые остаются скомпенсированными в этих телах. Что касается процесса электризации, то так же, как и в случае электризации отдельных атомов и молекул, он сводится обычно к переходу некоторого числа электронов от одного тела к другому. В виду малости массы электронов (а также малости их веса по сравнению с испытываемыми ими электрическими силами) изменение массы тел, связанное с потерей или приобретением ими даже очень большого числа электронов, остается практически совершенно незаметным.

§ 5. Свободные электроны в металлах. В случае изоляторов и электролитов электроны остаются прочно связанными с отдельными атомами или ионами, и потому присутствие их обнаруживается лишь косвенным образом. Иначе обстоит дело в случае металлов, отличительные свойства которых обусловливаются именно наличием электронов, способных перемещаться по всему объему тела. Подобные электроны называются свободными  том смысле, что они не связаны с определенными индивидуальными атомами, но могут переходить от одних атомов к другим. Эта относительная «свобода» не мешает им, однако, быть прочно связанными со всем коллективом атомов в его целом. Таким образом, с электрической точки зрения металлическое тело можно рассматривать как совокупность положительных ионов, спаянных друг с другом совокупностью «обобществленных» электронов.

Эта своеобразная особенность металлов находит себе выражение в том обстоятельстве, что ионы их, встречаемые в электролитах (а именно в растворах солей и щелочей), так же как ионы, водорода, всегда имеют положительный заряд. Это означает, что металлические атомы сравнительно легко отдают один или несколько электронов (в зависимости от своей валентности), но не обладают способностью удерживать посторонние электроны. При сближении металлических атомов друг с другом на достаточно малые расстояния слабо связанные электроны утрачивают связь с определенными атомами и начинают гулять от одного атома к другому, то есть становятся «свободными» в указанном выше смысле. По всей вероятности, такое же «освобождение» электронов, обусловливающее появление у соответствующего тела способности проводить электричество (и электризоваться через влияние), должно было бы наблюдаться также и у диэлектриков, подвергнутых достаточно большому всестороннему давлению. Покамест, однако, необходимых для этого давлений достигнуть не удалось. Обратно, при достаточном удалении металлических атомов друг от друга, например, при переходе металла в газообразное состояние, электроны должны связываться с отдельными атомами, также как и в случае диэлектриков. И действительно, опыт показывает, что все вещества в газообразном состоянии, в том числе и металлические пары, являются при обычных условиях изоляторами. Присутствие в металлах «свободных» электронов обнаруживается особенно отчетливо при высоких температурах (порядка тысячи или нескольких тысяч градусов). Будучи слабее связаны с металлом, как целым, нежели положительные ионы, электроны первые начинают испаряться, совершенно подобно тому, как при нагревании смеси двух жидкостей разной летучести, например, воды и спирта, вначале испаряется преимущественно более летучая жидкость. Испаряющиеся электроны образуют вокруг раскаленного металла нечто вроде атмосферы, которая удерживается притяжением остающегося на металле положительного заряда (подобно тому как атмосферный воздух удерживается притяжением земли), но может быть легко оторвана от него путем компенсации этого заряда зарядом противоположного знака¹).

¹) Испускание электронов раскаленными металлами и углем было впервые открыто Эдисоном и подробно изучено Ричардсоном; оно поэтому часто обозначается как «эффект Ричардсона».

Другим средством извлечения «свободных» электронов из металлов является освещение их ультрафиолетовыми (а в некоторых случаях и видимыми) лучами. Это явление, то есть вырывание электронов под действием света, носит название фотоэлектрического эффекта¹). Наблюдение фотоэлектрического эффекта (см. энергия) у очень маленьких (микроскопических) металлических пылинок показывает, что заряд их меняется не непрерывным образом, но скачкообразно, соответственно вылетанию одного за другим отдельных электронов. Таким путем Милликену удалось измерить чрезвычайно точно заряд электрона (см. материя, ХХVIIІ, 332/33); при этом получилась та же цифра, которая была получена ранее на основании данных электролиза для заряда водородных и других одновалентных ионов. Извлекши электрон из металла нагреванием или светом и исследуя движение его в пустоте под действием электрических и магнитных сил, можно определить отношение заряда электрона к его массе и таким образом, зная первый, вычислить последнюю. Для массы электрона в граммах получается число 9·10^-28 примерно в 2 000 раз меньшее, чем для массы водородного атома, то есть протона. Тот же результат можно получить, как показал Толмэн, и не вырывая электронов из металла, но исследуя электрический эффект, сопровождающий резкую остановку быстро движущегося металлического тела (например, быстро вращающегося диска). При этом электроны ведут себя совершенно так же, как пассажиры, находящиеся в вагоне трамвая при резкой остановке: они устремляются вперед по инерции. Это движение электронов по инерции чрезвычайно быстро, впрочем, прекращающееся, может быть легко обнаружено (в виде электрического тока), причем получаемый эффект оказывается пропорциональным отношению заряда электрона к его массе (ε/m). Таким образом, зная первый, оказывается возможным вычислить вторую.

¹) Последний был открыт в 80-х годах XIX века Столетовым и Гальваксом.

§ 6. Электризация проводников; распределение заряда и потенциала; емкость; конденсаторы; энергия и квазиупругие напряжения поля. Мы не будем углубляться в дальнейшее развитие электронной теории, так как изложенных результатов совершенно достаточно для понимания механизма различных электростатических явлений, и перейдем теперь к более подробному количественному рассмотрению наиболее важных из них. Явления эти разделяются на две категории, соответственно разделению тел с электростатической точки зрения на проводники и изоляторы. При этом в качестве проводников можно ограничиться практически одними лишь металлами. Основным вопросом электростатики проводников (металлов) является вопрос о пространственном распределении заряда, сообщаемого изолированному проводнику.

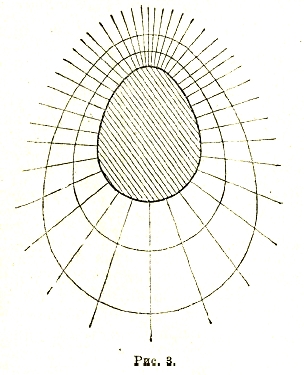
В виду подвижности электрических зарядов (электронов), в нем находящихся, избыточный (некомпенсированный) заряд должен распределиться таким образом, чтобы внутри проводника электрическое поле исчезло, то есть, чтобы весь проводник имел один и тот же потенциал V. Это условие, при котором поверхность проводника является одной из ряда эквипотенциальных поверхностей, характеризующей создаваемое им электрическое поле, оказывается выполненным при определенном распределении заряда проводника на его поверхности. Электрические силовые линии оказываются при этом направленными перпендикулярно к последней (рис. 3) и наибольшей густоты достигают в тех точках, где она имеет наибольшую кривизну. Этому сгущению их соответствует сближение эквипотенциальных поверхностей, расстояние между которыми согласно формуле (7) должно быть тем меньше, чем больше электрическая напряженность Е.

Потенциал наэлектризованного проводника V пропорционален его заряду е. Отношение

называется емкостью, или электроемкостью проводника. Емкость имеет размерность длины и в случае шаровидного проводника равна его радиусу. Работа, которую нужно затратить для того, чтобы увеличить заряд е на бесконечно малую величину de при данном потенциале V, равна, по определению потенциала, произведению Vde. Отсюда для полной (электростатической) энергии наэлектризованного проводника получается выражение

Это выражение непосредственно следует также из сделанного в § 1 замечания о том, что потенциальная энергия любой системы точечных зарядов равна половине суммы энергий каждого из них по отношению к остальным.

Для измерения потенциала проводника (а, следовательно, и его заряда), служат приборы, называемые электроскопами, или электрометрами. Они представляют собой проводники с подвижными частями (например, листочки электроскопа), которые при наличии одноименной электризации взаимно отталкиваются с силой, пропорциональной квадрату заряда. Обладая очень малой емкостью, эти приборы, будучи присоединены (металлической проволокой) к рассматриваемому проводнику, отнимают, у него очень малую долю его заряда, причем вся система принимает потенциал, практически не отличающийся от первоначального потенциала изолированного проводника (совершенно подобно тому, как это происходит при измерении температуры большого тела маленьким термометром).

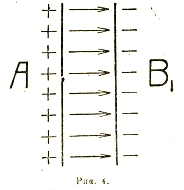
Если вблизи наэлектризованного проводника А поместить другой нейтральный В, то на ближайшей стороне последнего появляется заряд противоположного, а на отдаленной — того же знака (электростатическая индукция, см. рис. 2). При этом потенциал А (численно) уменьшается, благодаря действию зарядов, индуктированных им на В, а заряд А распределяется по его поверхности несколько иначе, чем при отсутствии В. Уменьшение потенциала А под влиянием В при неизменности заряда е_А можно рассматривать как результат увеличения емкости. Это увеличение емкости тем больше, чем больше проводник В и чем меньше его расстояние от А. Для максимального увеличения емкости А проводник В составляется из двух частей: небольшой части В₁, близкой по размерам и форме к А и помещаемой на очень маленьком от него расстоянии, и очень большой части В₂, соединенной с В₁ проволокой (рис. 4). Частью В₂ обычно служит земля, то есть земной шар. При таких условиях на В₁ индуктируется заряд приблизительно равный и противоположный А₁. Если заряд А отрицателен, то мы имеем дело с фактическим уходом в землю части электронов с В₁; в противном случае уход положительного заряда с В₁ в землю означает на самом деле приток электронов (в эквивалентном количестве) из земли к В₁. В результате получается прибор, называемый электрическим конденсатором в виду того, что он позволяет накоплять большие заряды при сравнительно малых потенциалах (см. конденсатор). Заметим, что потенциал системы В₁ В₂, то есть потенциал земли, обычно принимается за нуль, так как для определения напряженности поля существенны лишь разности потенциалов, а не их абсолютные знаки.

Рассмотрим для примера, а также для элементарного вывода некоторых важных общих соотношений случай шарового и плоского конденсатора. Первый образован двумя концентрическими шарами — внутренним (А) и внешним (В₁), который сцепляется с землей. Заряд, распределенный равномерно на поверхности шара, внутри его не создает никакого поля, а наружу действует таким же образом, как точечный заряд той же величины, сосредоточенный в центре шара. Отсюда следует, что потенциал на поверхности и внутри шара радиуса а с зарядом е равен е/а (что соответствует приведенному выше определению емкости шара). При этом считается, что потенциал обращается в нуль на бесконечном расстоянии. Если первый шар окружен вторым с радиусом b > а и с зарядом -е, то потенциал внутри первого шара оказывается равным е/а – е/b, а снаружи второго — нулю. Ничто не изменится поэтому, если мы второй шар соединим с землей. Электрическое поле между обоими шарами совпадает с полем внутреннего шара, то есть равно Е = е/r³, где r — расстояние от их общего центра (4).

Емкость внутреннего шара с = e/V_A определяется при том формулой V_A = e (1/a – 1/b), то есть равна с = аb/b – a, или приблизительно, если разность b — а = d мала в сравнении с а,

где S = 4πа² обозначает поверхность шара. Заметим, что напряженность поля на поверхности первого шара (с наружной стороны) связана с зарядом η = е/S, приходящимся на единицу его поверхности, соотношением

Такое же соотношение (с противоположным знаком) мы получаем для поверхности второго шара (с внутренней стороны). Вырезав из нашего шарового конденсатора маленький кусок, образованный двумя почти плоскими поверхностями, линейные размеры которых велики в сравнении с их расстоянием d, мы получим плоский конденсатор (рис. 4).

Емкость его по-прежнему будет определяться формулой (10), если подразумевать в ней под S площадь каждой из пластин (А или В₁). Остается также в силе и соотношение (11) для поля внутри него. Поле это (в противоположность случаю шарового конденсатора) слагается из двух равных частей, зависящих соответственно от обеих пластин. Таким образом, поле каждой пластинки можно считать однородным, то есть независящим от расстояния (поскольку последнее мало в сравнении с поперечными ее размерами), и равным 2πη. Отсюда следует, что сила притяжения между обеими пластинками не зависит от их расстояния и равна 2πηе = 2πη²S. Работа, которую нужно затратить для того, чтобы раздвинуть обе пластинки на расстояние d, равна, следовательно,

где V = Sd объем пространства, заключенного между пластинками конденсатора, где действует поле с напряженностью Е = 4πη (вне этого объема поле практически отсутствует).

Итак, мы видим, что для создания однородного поля Е в объеме V необходимо затратить энергию Е²/8π V, пропорциональную объему поля и квадрату его напряженности. Этот результат показывает, что электрическую энергию можно рассматривать как величину, локализуемую в пространстве, непосредственно связанную с электрическим полем и распределенную в нем с объемной плотностью

Это определение энергии совпадает с тем, которое получается из формулы (9), если подставить в нее выражения (11) для с и (10) для Е. В самом деле, полагая

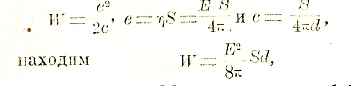
где множитель Sd представляет собой объем электрического поля. Заметим, что плотность энергии

 

численно совпадает с силой притяжения, действующей на единицу площади одной из пластинок конденсатора со стороны другой. Этот результат также легко обобщается на случай произвольной системы заряженных проводников. Его можно представить себе наглядным образом, рассматривая электрические силовые линии как растянутые упругие нити, а силу

как упругое напряжение вдоль этих нитей, отнесенное к единице площади перпендикулярной к ним поверхности. Это представление было введено Максуэлом, который дополнил его представлением о поперечном давлении (или «распоре») электрических силовых линий той же самой величины, как и продольное натяжение.

Таким образом, электростатические явления могут быть описаны двумя различными способами. Во-первых, как то или иное распределение на проводниках (или внутри них) подвижных электрических зарядов, действующих друг на друга через отделяющее их пустое пространство по закону Кулона. И, во-вторых, как то или иное распределение в этом пространстве электрического поля, связанного с определенной энергией, а также определенными квазиупругими напряжениями, которые, «зацепляясь» за поверхность проводников, вызывают наблюдаемые, взаимодействия между ними. В первой картине основной, первичной реальностью являются электрические заряды (вернее заряженные материальные частицы), тогда как электрическое поле играет вспомогательную роль своего рода посредника между ними. А именно, вместо того, чтобы рассматривать действие заряда е_А на заряд е_В как нечто непосредственно данное (законом Кулона), мы можем рассматривать его, как результат действия на заряд В (или А) электрического поля, создаваемого зарядом А (или В). Без всякого ущерба для результатов можно было бы при этом понятие поля совершенно исключить из рассмотрения. Наоборот, во второй картине основной первичной реальностью является именно электрическое поле; электрические заряды рассматриваются здесь просто как начальные или конечные точки силовых линий (то есть как те точки, где эти линии зацепляются за материальные тела) и не играют никакой самостоятельной роли. Поскольку при этом с силовыми линиями как таковыми не связываются никакие материальные представления, обе картины являются формально эквивалентными.

Однако, фактически вторая картина, «картина поля», развилась (в XIX веке) в связи с представлением о том, что электрические силы обусловлены упругими напряжениями в некоторой материальной среде – эфире — наполняющей пространство, которое нам кажется совершенно пустым. Энергия поля и максуэловские напряжения рассматривались при этом как упругая энергия и упругие напряжения, обусловленные деформацией эфира. Отвергая эфир как совершенно ненужную фикцию и рассматривая электрические заряды как неотъемлемое свойство элементарных частиц материи (электронов и протонов), мы, естественно, несмотря на формальную эквивалентность первой и второй картины, должны отдавать принципиальное предпочтение первой, как выражающей реальные соотношения наиболее непосредственным образом (подробнее см. физика, особенно XLIII, 325 сл.).

§ 7. Поляризация диэлектриков. Вопрос о равновесном распределении электрического заряда на поверхности (или внутри) изолирующего (диэлектрического) тела не имеет смысла, так как, в виду отсутствия свободных электронов в подобном теле, сообщенный ему (путем прибавления или отнятия некоторого количества связанных электронов) заряд может оставаться неопределенно долгое время на одном и том же месте. Поэтому электростатика диэлектриков заключается в изучении той поляризации, которую они испытывают в электрическом поле, исходящем от заряженных проводников. Как уже указывалось в § 2, поляризация эта сводится, вообще говоря, к смещению зарядов противоположного знака внутри отдельных молекул в противоположные стороны, положительных — в направлении поля (то есть вектора, напряженности ), а отрицательных — в противоположном направлении. В тех случаях, когда молекулы тела построены из противоположно заряженных ионов и могут более или менее свободно вращаться, поляризация тела вызывается не только поляризацией молекул, но и их ориентацией. Последняя происходит путем поворота электрических осей молекул, то есть прямых, проведенных от их отрицательных концов к положительным, в направлении электрического поля. Нейтральная частица, образованная совокупностью двух равных и противоположных электрических зарядов (±е), смещенных по отношению друг к другу на некоторое очень маленькое расстояние d, называется электрическим диполем; свойства подобного диполя характеризуются вектором, равным произведению ed и направленным от отрицательного заряда к положительному. Этот вектор называется моментом диполя, или электрическим моментом.

Молекулы поляризованного тела, независимо от происхождения этой поляризации (путем деформации или ориентации), можно представить себе схематически в виде подобных диполей, с электрическими моментами, параллельными электрическому полю в соответствующей точке и в первом приближении пропорциональными его напряженности Е. При этом следует учитывать не только внешнее поле, в которое вводится диэлектрик, но также и то поле, которое им самим создается вследствие его поляризации. Внутри поляризованного диэлектрика электрические заряды составляющих его диполей обычно взаимно компенсируются. Некомпенсированными, таким образом, остаются лишь крайние заряды, то есть обнаженные (наружные) концы диполей, образующих его поверхность (точнее поверхностный слой), поскольку оси не параллельны поверхности. В результате, поляризованный диэлектрик в отношении испытываемых и производимых им действий оказывается эквивалентным проводнику с надлежащим образом распределенным поверхностным зарядом. Общая величина этого заряда должна, конечно, равняться нулю (в виду нейтрального диэлектрика); соответственно этому на различных (обычно противоположных) участках поверхности он принимает разные знаки.

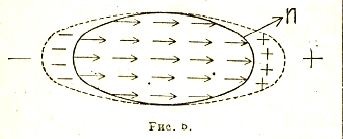
На рис. 5 представлен равномерно поляризованный диэлектрик. Стрелки обозначают образующие его диполи, а толщина ограниченного пунктиром слоя характеризует поверхностную плотность эквивалентного заряда, то есть «связанный» заряд, приходящийся на единицу поверхности. Легко показать, что эта плотность η равна проекции на внешнюю нормаль   к поверхности в соответствующей точке так называемого вектора поляризации  , равного (геометрической) сумме моментов диполей, содержащихся в единице объема тела, или, короче, электрическому моменту единицы объема. Мы имеем, следовательно, соотношение

Следует заметить, что взаимная компенсация зарядов диполей внутри поляризованного диэлектрика не всегда бывает полной. Поэтому в общем случае поляризация оказывается эквивалентной определенной электризации тела не только по поверхности, но и по объему. Если к наэлектризованному проводнику А поднести диэлектрик В, то на поверхности последнего появляется, благодаря поляризации, связанный заряд, сходный по своему распределению со свободным зарядом, который был бы индуктирован проводником А на теле В, если бы оно являлось также проводником. Естественно, однако, ожидать, что связанные поверхностные заряды, обусловленные смещением электронов в отдельных молекулах, должны быть меньше поверхностных зарядов, образованных перемещением электронов в проводнике тех же размеров и формы. Соответственно этому взаимное притяжение А и В, а также понижение потенциала А, вызываемое В, должно быть меньше в случае диэлектрика, чем в случае проводника. Отношение этих эффектов друг к другу может служить приблизительной мерой степени связанности электронов в рассматриваемом диэлектрике. В случае абсолютно связанных электронов диэлектрик В не испытывал бы со стороны А и не оказывал бы на него никакого действия. Необходимо, впрочем, заметить, что рассматриваемое отношение зависит не только от внутренних свойств тела В, но также от его геометрических свойств и положения по отношению к А. Чтобы отвлечься от этих несущественных обстоятельств, представим себе, что тело В окружает А со всех сторон, заполняя все пространство от поверхности А и до бесконечности. Этот случай мы имеем, когда проводник А находится в однородной диэлектрической среде В (например, воздухе, масле и т. д.) достаточно больших, то есть практически неограниченных размеров. При этом на поверхности В, прилежащей к А, появляется связанные заряд -е', частично нейтрализующий свободный заряд +е, покрывающий поверхность А. Таким образом, на пограничной поверхности (АВ) остается фактически лишь некомпенсированный заряд е'' = е — е', которым и определяется результирующее электрическое поле Е, создаваемое проводником в окружающем диэлектрике.

Обычно — в огромном большинстве встречающихся на практике случаев — заряд е', а следовательно и е'' прямо пропорционален заряду е, причем эта пропорциональность относится не только к полным зарядам, но и к зарядам, приходящимся на любой участок поверхности, то есть к поверхностным плотностям η, η', η''. При таких условиях электрическое поле, создаваемое проводником А в пустом пространстве при погружении его в диэлектрическую среду, сохраняет ту же самую структуру, но лишь ослабляется в отношении е : е''. Коэффициент

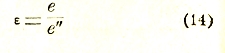
характеризует внутренние электрические свойства диэлектрической среды и называется диэлектрической постоянной ее ¹).

В случае проводящей среды мы имели бы, очевидно, е' = -е и е'' = 0, то есть ε = ∞. Таким образом, с электростатической точки зрения проводник можно рассматривать как изолятор с диэлектрической постоянной, равной бесконечности, а пустоту — как изолятор с диэлектрической постоянной ε = 1. Диэлектрическая постоянная может служить мерой степени «свободы» или «смещаемости» электронов в молекулах диэлектрика, а обратная ей величина — мерой степени их связанности. Впрочем, последнюю представляется более естественным характеризовать величиной отношения е'/е, равного 1 — 1/ε.

Если в однородную диэлектрическую среду с постоянной ε погружено несколько проводников с зарядами е_А, е_В и т. д., то так же, как и в случае одного проводника, создаваемое ими электрическое поле не изменяет своей структуры и лишь ослабляется в ε раз (по сравнению с пустотой); действие среды сводится, следовательно, к замене свободных зарядов е_А, е_В.... «эффективными»

Вместе с напряженностью поля изменяется, и притом в том же самом отношении, и потенциал или разность потенциалов между любыми двумя точками. Применяя этот результат к электрическому конденсатору, мы видим, что емкость его с при погружении в диэлектрическую среду с постоянной ε должна увеличиваться в ε раз (при этом емкость определяется по-прежнему, как отношение свободного заряда А к его потенциалу или, вернее, к разности потенциалов между А и В). Следует заметить, что в случае конденсатора погружение в безграничную диэлектрическую среду можно заменить введением этой среды в тот небольшой объем, в котором сосредоточено его электрическое поле.

¹) Или диэлектрическим коэффициентом.

Присутствие этой среды в остальном пространстве, где поле равно нулю, очевидно, не имеет никакого значения. Таким образом, вводя между пластинками, или, как их называют, «обкладками», плоского конденсатора слой диэлектрика (жидкого или твердого), который заполняет все пространство между ними, мы повышаем электроемкость конденсатора в ε раз, где ε — диэлектрическая постоянная изоляционной прокладки.

Переходя от напряженности поля к электрической силе, с которой действуют друг на друга проводники, погруженные в диэлектрическую среду, мы получаем разные результаты в зависимости от того, в какой мере мы при этом отделяем проводники от среды. Обычно последняя учитывается лишь при определении эффективного поля, создаваемого одним из проводников (А). Сила, испытываемая с его стороны каким-нибудь другим проводником В, определяется при этом независимо от наличия диэлектрика, то есть исходя из свободного, а не эффективного заряда В. При таком условии сила, а следовательно и энергия, оказывается уменьшенной в ε (а не в ε²) раз, то есть в том же отношении, как и напряженность поля. Силу, с которой проводник А с его эффективным зарядом е_А/ε действует на связанный заряд

, прилегающий к В,  представляется естественным отнести не к проводнику В, но к окружающему его диэлектрику. Эти соображения применимы, разумеется, и к взаимодействию тех элементов, из которых слагается заряд каждого проводника, взятый в отдельности. Таким образом, например, энергия проводника с зарядом е, емкость которого в пустоте равна с, при погружении в диэлектрическую среду с постоянной ε, оказывается равной не

, что соответствует замене емкости с на εc. То же самое относится и к конденсаторам. Заметим, что уменьшение энергии, то есть разность

можно при этом рассматривать как энергию, связанную с поляризацией самой среды зарядом А. Отрицательный знак этой энергии становится вполне естественным, если мы примем во внимание, что связанные электроны в молекулах перемещаются при поляризации диэлектрика в направлении девствующих на них сил; таким образом, последние совершают положительную работу за счет электрической энергии всей системы.

Произведение диэлектрической постоянной на напряженность поля, то есть вектор

называется электрической индукцией (или «электрическим смещением»). В случае однородной среды этот вектор равен напряженности того поля, которое получилось бы при ее устранении, то есть которое зависит от свободных зарядов проводников. У самой поверхности одного из проводников мы имеем соотношения

, где η, η' и η'' представляют собой поверхностные плотности соответственно свободного, связанного и эффективного заряда. Принимая во внимание, что плотность η' равна согласно (13) поляризации  диэлектрика у поверхности проводника, мы получаем соотношение

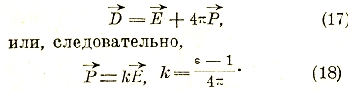
Коэффициент k называется электрической восприимчивостью среды; диэлектрическая постоянная выражается через него формулой

Нетрудно показать, что предыдущие соотношения остаются справедливыми не только вблизи поверхности проводников, но и для любой точки поляризованного диэлектрика.

Имея ввиду взаимодействие проводников через диэлектрик, последнему приписывают энергию, распределенную в нем с объемной плотностью

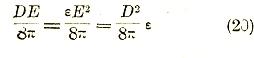
и численно равные последней квазиупругие напряжения (продольное натяжение и поперечный распор). При этом, однако, исключается из рассмотрения энергия, связанная с поляризацией самого диэлектрика. Эта энергия получается из предыдущей путем вычитания из нее энергии, соответствующей отсутствию диэлектрика. Считая последнюю распределенной с объемной плотностью D²/8π, мы получаем для первой объемную плотность

Она соответствует энергии -1/2Ер каждого элементарного диполя, из которых слагается поляризованный диэлектрик во внешнем поле Е.

Теория поляризации диэлектриков ограниченных размеров и их воздействия на поляризующие проводники представляет собой большие трудности. Она основывается на том обстоятельстве, что при переходе из пустоты в диэлектрик или через границу двух разных диэлектриков нормальная (перпендикулярная к пограничной поверхности) проекция «индукции»  и тангенциальная (касательная) проекция напряженности  остаются непрерывными. Эти «пограничные условия» легко выводятся из рассмотрения связанного заряда, находящегося на пограничной поверхности. Плотность последнего η связана с разностью нормальных слагающих напряженности  с обеих сторон поверхности формулой

, а с разностью нормальных слагающих поляризации  формулой

.

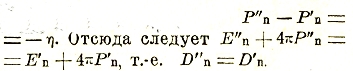Непрерывность касательной проекции  явствует непосредственно из того обстоятельства, что поверхностный заряд не создает тангенциального поля. В заключение отметим основные результаты, относящиеся к величине диэлектрической постоянной у разных диэлектриков. В случае газов она весьма близка к 1, причем разность ε — 1, т есть, следовательно, восприимчивость, прямо пропорциональна плотности, как и следует ожидать, если вспомнить, что восприимчивость определяет электрический момент приобретаемой в данном поле  единицей объема среды. Поскольку в газе молекулы практически не действуют друг на друга, этот момент должен быть пропорционален числу их в единице объема, то есть плотности. В случае жидкостей и твердых тел плотности пропорциональна величина

которая при близости ε к 1 обращается в восприимчивость k. У «гомополярных» веществ, молекулы которых не обладают постоянным электрическим моментом, диэлектрическая постоянная не зависит от температуры, что весьма естественно, если принять во внимание, что она обусловливается смещением электронов в отдельных атомах. У гетерополярных веществ с дипольными молекулами в газообразном состоянии восприимчивость выражается суммой

где k₀ и с обозначают постоянные, а Т — абсолютную температуру. Первый член характеризует ту часть восприимчивости (то есть поляризации газа), которая обусловливается смещением электронов внутри атомов или ионов, а второй, обратно пропорциональный температуре, — часть, обусловленную ориентацией молекул.

Тепловое движение стремится нарушить правильную ориентацию, вызываемую электрическим полем, чем и объясняется зависимость средней их ориентации от температуры. Формула (23) применима лишь при не очень низких температурах, причем постоянная с выражается через момент р отдельных молекул и число их N в единице объема формулой

где k — так называемая идеальных газов (3/2kТ – средняя кинетическая энергия теплового движения одной молекулы газа). При очень низких температурах все молекулы, поскольку они сохранили бы при этом свободу вращения, были бы полностью ориентированы даже сравнительно слабым полем. В той мере, в которой поляризация тела зависит от ориентации молекул, она достигла бы максимальной величины или, как говорится, «насыщения». Само собой разумеется, что в области близкой к насыщению о пропорциональности между поляризацией и напряженностью поля не может быть и речи. Впрочем, на опыте эта пропорциональность соблюдается весьма хорошо. Это объясняется, с одной стороны, невозможностью исследовать область низких температур при сохранении свободы вращения молекул (так как при низких температурах происходит затвердение вещества, а в твердом теле молекулы, как правило, утрачивают способность вращаться), а с другой стороны, практической невозможностью достигнуть полей, необходимых для «насыщения» поляризации при обычных температурах.

Диэлектрическая постоянная твердых и жидких веществ, молекулы которых не являются постоянными диполями, представляет собой величину, не зависящую от температуры и обычно колеблющуюся в пределах нескольких единиц (например, стекло, фарфор 6-7, эбонит 2,5). В случае дипольных жидкостей она может достигать при обычной температуре нескольких десятков (например, 30-40 у спиртов, 80 у воды, 95 у синильной кислоты) и даже сотен¹). Недавно обнаружилось, что у некоторых твердых тел со сложными дипольными молекулами диэлектрическая постоянная может достигать в узком температурном интервале колоссальных значений (до 25 000 у сегнетовой соли, согласно опытам Курчатова и Кобеко в Физико-техническом институте А. Ф. Иоффе).

¹) Для электрического момента одной молекулы получаются при этом значения порядка 10^-18.

§ 8. Математическая теория электростатических явлений. а. Теорема Гаусса. Как уже указывалось в § 1, электрическое поле изображается наглядным образом при помощи силовых линий, совпадающих по направлению с направлением электрической напряженности и пропорциональных последней по своей густоте вблизи соответствующей точки. Количество силовых линий, пересекающих данную поверхность S, представляет собой меру так называемого электрического потока через эту поверхность. При определении величины потока, линии, идущие в одну сторону, соответствующую направлению нормали к поверхности, считаются со знаком +, а линии, идущие в противоположную сторону, со знаком -. Другими словами, электрический поток Ф через поверхность S определяется как разность между числом силовых линий, идущих через нее в положительном и отрицательном направлении. Густота линий определяется при этом таким образом, чтобы число линий, пересекающих перпендикулярную к ним единичную площадку, совпадало с численным значением электрической напряженности Е.

При этом условии электрический поток dФ через бесконечно малую площадку dS, нормаль к которой образует угол α с направлением силовых линий (то есть направлением ),

определяется формулой

где Е_n обозначает слагающую (проекцию) в направлении нормали

Рассматривая электрический поток через замкнутую поверхность S, обусловленный точечным зарядом е, нетрудно показать на основании закона Кулона, что этот поток равен нулю, если заряд находится вне поверхности, и 4πе, если он находится внутри нее (положительным направлением считается при этом направление внешней нормали к поверхности S). В самом деле, полагая в (24)

 и замечая, что 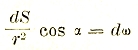 представляет собой телесный угол, под которым виден элемент поверхности dS из соответствующей точки со знаком +, если последняя находится внутри S, и знаком - в противоположном случае, получаем

Этот результат легко обобщается на случай любой системы зарядов е_А, е_В и т. д., как внутренних, так и внешних (ибо из формулы Е_n = Е_An + Е_Bn +... следует, что общий электрический поток от всех этих зарядов равен алгебраической сумме потоков от каждого из них в отдельности). Таким образом, обозначая через е результирующий электрический заряд, находящийся внутри S, мы получаем следующую общую формулу:

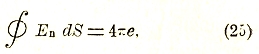
где кружок на знаке интеграла указывает на замкнутость поверхности S.

Из этой формулы, данной впервые Гауссом, между прочим, следует, что электрические силовые линии не могут начинаться или обрываться в пустом пространстве, но что они начинаются на положительных зарядах и кончаются на отрицательных.

b. Уравнения Пуассона и Лапласа. Если представить себе, что заряд е не сконцентрирован в отдельных точках, но распределен непрерывным образом с объемной плотностью ρ, то можно положить в (25)

где dv представляет собой элемент объема, заключенного внутри S, а интегрирование распространяется на весь этот объем.

С другой стороны, поверхностный интеграл, стоящий в левой части (25), может быть преобразован в объемный по следующей (данной Гауссом) формуле:

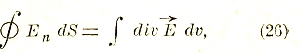
где символ div, называемый «расхождением» вектора  в прямоугольной системе координат x, у, z выражается формулой

Из равенства

 в связи с произвольностью поверхности S, вытекает дифференциальное уравнение

называемое уравнением Пуассона. Это уравнение само по себе еще не эквивалентно закону Кулона. Оно становится эквивалентным последнему в связи с равенством

где V обозначает электрический потенциал, а grad V — градиент (см. тензориальное исчисление, XLI, ч. 7, 311), вектор с прямоугольными слагающими

Напомним, что равенство (29) выражает консервативный характер электростатических сил (§ 1). Легко показать, что оно эквивалентно тождественному (то есть выполняющемуся для всего пространства) уравнению

где символ rot (или curl), называемый вихрем, или ротором, представляет собой вектор, слагающие которого по осям х, у, z равны соответственно

Подставляя (29) в (28), мы получаем дифференциальное уравнение второго порядка (Лапласа) для электрического потенциала

В частном случае пустоты (ρ = 0) оно обращается в обычное уравнение Лапласа

с. Энергия и напряжение. В случае электрического заряда, распределенного в пространстве непрерывным образом, электростатическая энергия W определяется как полусумма энергий каждого из его бесконечно малых элементов по отношению ко всем остальным, то есть как интеграл

¹) Дифференциальный оператор (набла, оператор Гамильтона)  выражает в символическом виде пространственное дифференцирование так, как, например,d/dx обозначает символически частное дифференцирование по x.

Этот интеграл с помощью уравнения (33) и соотношения (29) может быть преобразован в интеграл

взятый по всему электрическому полю, создаваемому рассматриваемым зарядом (а не только по объему последнего). Соответственно этому, электрическую энергию можно представлять себе не как выражение взаимодействия между разными зарядами или элементами одного и того же заряда, но как величину, непосредственно связанную с электрическим полем. Необходимо, однако, иметь в виду, что подобное представление имеет смысл только в том случае, если мы имеем дело с зарядом, распределенным с конечной объемной или также поверхностной плотностью, и учитываем взаимодействие между всеми бесконечно малыми его элементами. Таким образом, например, энергия системы, образованной некоторой совокупностью электронов и протонов, может быть представлена в форме (36) только при том условии, если мы будем рассматривать эти частицы не как точечные заряды, а как некоторые протяженные образования (например, шарики) с объемным или поверхностным зарядом и будем учитывать не только взаимодействие между разными частицами, но также и взаимодействие между элементами одной и той же частицы. Существенно положительный знак энергии (36) объясняется тем обстоятельством, что энергия внутричастичных сил, являющихся силами отталкивания, всегда больше энергии междучастичных сил (поскольку расстояния между разными частицами больше их собственных размеров).

Сила, действующая на некоторый заряд, заключенный в объеме v, непосредственно выражается интегралом

Здесь под подразумевается напряженность электрического поля, обусловленного не только зарядами, находящимися вне объема v, но и элементами самого заряда е. Так как, однако, силы взаимодействия между ними попарно равны и противоположны, то интеграл (37) определяет фактически лишь внешнюю силу, которую заряд е испытывает со стороны зарядов, находящихся вне объема v.

Пользуясь уравнением Пуассона (28), можно преобразовать объемный интеграл (37) к интегралу

Распространенному по поверхности S, его ограничивающей, где есть вектор со слагающими

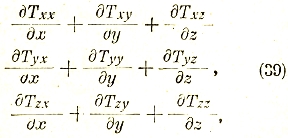
а величины Т_хх, Т_уу, T_zz, Т_ху = Т_ух, T_yz = T_zy, T_zx = T_xz представляют собой слагающие максуэловского тензора напряжений  (значок ² характеризует ранг этого тензора). Эти слагающие выражаются через слагающие электрической напряженности по формулам

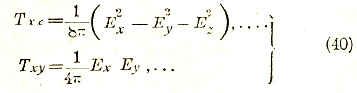
и сводятся к уже упомянутым нами выше напряжению вдоль и давлению поперек силовых линий. Таким образом, сила, испытываемая зарядом, находящимся внутри объема v со стороны зарядов, находящихся вне этого объема, может быть представлена как результат «квазиупругих» напряжений, распределенных на пограничной поверхности.

d. Электризация проводников и поляризация диэлектриков. Вопрос о распределении электрического заряда на поверхности проводника или системы проводников решается обычно путем интегрирования уравнения Лапласа для потенциала того поля, которое ими создается в окружающем пространстве, в связи с условиями V = const для поверхности каждого проводника; поверхностная плотность электрического заряда, его покрывающего, определяется при этом соотношением

где dV/dn обозначает производную потенциала по внешней нормали. Если общий заряд проводника задан, то величина его служит для фиксирования величины потенциала. Наоборот, задание величины потенциала (например, в случае заземленного проводника) служит для определения величины заряда.

Уравнение Лапласа справедливо и в том случае, когда проводники погружены в однородную диэлектрическую среду. При этом, однако, в соотношениях (41) напряженность поля следует заменить электрической индукцией. Легко далее, показать, что в общем случае, при наличии в неоднородном диэлектрике свободных зарядов, объемная плотность последних связана с таким же образом, как в случае пустоты с, то есть уравнением

Это уравнение, превращающееся в при ρ = 0, в случае резкого перехода от одного диэлектрика к другому превращается в пограничное условие, формулированное в конце предыдущего § (непрерывность нормальной слагающей).

Вместе с уравнением (29) или (31) оно дает возможность определить однозначным образом распределение поля в пространстве, содержащем наряду с проводниками любые диэлектрики.