Электричество. Глава II. Электрический ток

Глава II. Электрический ток. § 1. Основные понятия и величины; законы Ома и Джоуля. Электрический ток обычно определяется как «движение электричества». Необходимо, однако, иметь в виду, что движение нейтральной материи, поскольку последняя состоит из наэлектризованных частиц, должно было бы с точки зрения этого определения также представлять собой электрический ток. Таким образом, под электрическим током мы можем понимать лишь такое движение электричества, в котором противоположные заряды принимают неодинаковое участие либо в смысле своего количества, либо скорости или же того и другого. Электрический ток должен, следовательно, сопровождаться переносом электрического заряда от одного места к другому. Подобного рода перенос мы имеем, например, при электризации какого-либо проводника путем электростатической индукции, а также при поляризации диэлектрика; само собой разумеется, что по достижении равновесия ток в обоих случаях прекращается.

Наряду, однако, с подобными кратковременными токами, мы имеем в природе и, в особенности, в технике длительные токи, могущие продолжаться без всякого изменения неограниченно долгое время. Такого рода постоянные, или «стационарные» токи текут по замкнутым линиям, причем перенос электричества в этом случае не сопровождается каким-либо изменением в его распределении: на смену уходящим зарядам к каждому элементу объема притекают такие же самые заряды и в том же самом количестве с другой стороны. В простейшей своей форме стационарные электрические токи осуществляются в металлических проволоках, образующих замкнутые контуры. В этом случае ток состоит в движении одних лишь электронов, тогда как металлические ионы остаются неподвижными. В случае неметаллических тел (например, электролитов) перенос электричества осуществляется как положительными, так и отрицательными ионами (в частности электронами), причем противоположно заряженные частицы, поскольку движение их обусловливается тем или иным электрическим полем, движутся в противоположные стороны в соответствии с противоположными направлениями действующих на них электрических сил.

В отношении переноса электричества движение зарядов какого-либо знака в одну сторону совершенно эквивалентно движению зарядов противоположного знака в противоположную сторону. Количество электричества, переносимое в единицу времени через какую-либо (незамкнутую) поверхность S представляет собой меру силы электрического тока, протекающего через эту поверхность. Легко показать, что сила тока, протекающего через единичную площадку в направлении нормали ее,равна сумме произведений Nev_n для всех частиц, участвующих в движении, где N представляет собой число частиц каждого рода в единице объема, е — их заряд, а v_n — слагающая их скорости в направлении.

Вектор

называется плотностью тока. Он численно равен силе тока через единичную площадку, ориентированную наиболее выгодным образом. Заметим, что произведение заряда частицы е на ее скорость представляет собой аналог механического «количества движения», то есть произведения массы частиц на ее скорость. На этом основании вектор можно было бы назвать электрическим количеством движения рассматриваемой частицы, а вектор плотности тока определить независимо от выбора той или иной поверхности как электрическое количество движения в единице объема проводника, или, другими словами, как объемную плотность электрического количества движения.

В случае металлов электрический ток, как уже упоминалось выше, обусловливается движением одних лишь электронов. А так как последние имеют отрицательный заряд, то согласно определению вектора движение их происходит в направлении, противоположном направлению тока (то есть направлению переноса положительного электричества). В электролитах ток обусловливается движением + и - ионов в противоположные стороны.

Что касается диэлектриков, то в них стационарный ток является невозможным. Однако, и в этом случае всякое смещение связанных электронов внутри молекул или изменение ориентации последних составляет электрический ток, плотность которого пропорциональна скорости изменения поляризации. В самом деле, рассматривая молекулы как диполи с переменными электрическими моментами, нетрудно показать, что электрическое количество  движения отдельной молекулы равно скорости возрастания ее момента, то есть производной последнего по времени

Отсюда для объемной плотности тока в диэлектрике получаем

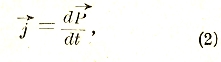
где — поляризация диэлектрика, то есть момент единицы объема.

В случае диэлектриков постоянное электрическое поле вызывает, как мы видели в предыдущей главе [ср.(18)], пропорциональную ему постоянную поляризацию

величина которой определяется условием равновесия между «внешними» электрическими силами, стремящимися раздвинуть противоположные заряды в противоположные стороны, и силами притяжения между этими зарядами (или между ориентирующими силами и дезориентирующим влиянием теплового движения). В случае проводников, поскольку дело касается «свободных» зарядов, подобные внутренние удерживающие силы отсутствуют. Если, бы эти заряды были абсолютно свободны, то есть не испытывали никаких иных сил, кроме внешней силы е, то под влиянием ее они стали бы двигаться равномерно ускоренно с ускорением, равным отношению этой силы к их массе. Подобные условия осуществляются, однако (и то не всегда), лишь в очень разреженных газах. В металлах и других проводниках «свободные», то есть подвижные, электроны и ионы оказываются вынужденными пробираться между связанными частицами — заряженными или нейтральными, взаимодействие с которыми вызывает их быстрое торможение. Это торможение можно рассматривать как силу трения, которая при малых скоростях должна быть прямо пропорциональна скорости и противоположна ей по направлению. Уравнение движения «свободных» частиц под совместным действием этой силы трения и внешней силы имеет вид

где f — коэффициент пропорциональности, равный отношению силы трения и скорости. В случае постоянного (то есть не зависящего от времени) поля скорость частиц, достигнув предельной величины

при которой внешняя сила уравновешивает силу трения, остается затем постоянной.

Таким образом, в противоположность совершенно связанным электронам, которые под влиянием постоянной внешней силы получают пропорциональное ей смещение, и совершенно свободным, которые приобретают пропорциональное ей ускорение, «полусвободные» электроны и ионы в проводящих телах получают при этом пропорциональную внешнему полю скорость. Умножая последнюю на заряд частицы, а также на число подобных частиц в единице объема, и оставляя сумму этих выражений для «полусвободных» частиц разных сортов, если таковые имеются, мы получаем по определению плотность тока. Таким образом, последняя оказывается связанной с напряженностью поля соотношением

где коэффициент пропорциональности σ, называемый удельной электропроводностью¹) данного проводника, выражается формулой

Заметим, что величина ρ = 1/σ — обратная σ, называется удельным сопротивлением. Пропорциональность между плотностью тока и напряженностью вызывающего его поля представляет собой основной закон в учении об электрическом токе, называемый законом Ома (см. XXX, 589).

¹) Или удельной электрической проводимостью.

Справедливость его показывает, что движение «полусвободных» зарядов в проводниках совершается на самом деле достаточно медленно для того, чтобы сила трения оставалась пропорциональной скорости.

Всякое движение с трением сопровождается нагреванием. В случае движения «полусвободных» зарядов в проводнике механизм этого нагревания заключается в передаче ими той кинетической энергии, которую им сообщает внешняя сила, связанным частицам, обусловливающим их торможение. Увеличение энергии колебаний этих связанных частиц (например, ионов металла) означает не что иное, как нагревание образуемого ими тела. Количество тепла Q, выделяющегося в единице объема проводника за единицу времени, должно равняться работе, произведенной за то же время внешними силами. В случае одной частицы эта работа равна произведению силы еЕ на скорость v. Мы получаем таким образом

или, следовательно, согласно (1)

Эта формула выражает так называемый закон Джоуля. Здесь теплота Q выражена в механических единицах (эргах). Для того, чтобы выразить ее в (малых) калориях, необходимо разделить Q на 4,2·10⁷ (= число эргов в одной калории).

§ 2. Прохождение электрического тока через разные тела (электропроводность). Удельная проводимость различных веществ колеблется в очень широких пределах. Наибольшей величины она достигает у металлов. В принятых нами (электростатических) единицах она выражается в этом случае цифрами порядка 10¹⁵-10¹⁷. Это значит, что под действием электрического поля с напряженностью равной 1 (то есть такой напряженностью, которая могла бы быть обусловлена единицей заряда на единице расстояния) в металле через поперечное сечение в 1 кв. см переносится в 1 секунду примерно 10¹⁶ единиц электричества, или, следовательно, приблизительно

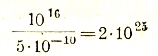
электронов. Принимая во внимание, что в единице объема металла содержится примерно столько же свободных электронов, сколько и атомов, то есть около 10²³, мы видим, что при указанных, условиях электроны должны двигаться со скоростью порядка 100 см в секунду.

При этом электропроводность металлов с понижением температуры увеличивается приблизительно обратно пропорционально абсолютной температуре и еще быстрее в области низких температур. У некоторых металлов (например, ртуть, олово) вблизи абсолютного нуля температуры электропроводность становится внезапно (при понижении температуры на одну сотую или даже тысячную градуса) бесконечно большой. Подобное состояние называется «сверхпроводимостью», а металлы, в нем находящиеся, называются «сверхпроводниками». В сверхпроводниках закон Ома не имеет места. Под влиянием внешних электрических сил электроны в них движутся так, как они двигались бы в пустом пространстве, то есть с ускорением, пропорциональным силе. Соответственно этому прохождение тока в сверхпроводнике не сопровождается выделением тепла и не прекращается по устранении вызвавших его сил, продолжаясь без заметного ослабления в течение нескольких суток. При обычных условиях ток в металле практически мгновенно следует за изменением внешней электрической силы, тотчас же исчезая по ее устранении.

Электролиты, то есть водные растворы солей, кислот и щелочей, обладают гораздо меньшей проводимостью, нежели металлы, как вследствие меньшего числа подвижных зарядов (ионов) в единице объема N, так и вследствие меньшей их подвижности, то есть большего коэффициента трения f (ср. формулу 5). При этом с повышением температуры электропроводность их не уменьшается, как у металлов, но, наоборот, увеличивается, что объясняется уменьшением коэффициента трения f вследствие уменьшения вязкости той жидкой среды — воды, в которой происходит движение ионов, а также увеличением степени диссоциации, то есть числа подвижных ионов N при том же числе растворенных молекул N₀. Напомним, что эта диссоциация не вызывается, но лишь облегчается действием воды; причиной ее, так же как и всякого другого химического разложения, является тепловое движение. При постоянной температуре степень диссоциации зависит, вообще говоря, от концентрации раствора, увеличиваясь с его разбавлением, то есть с увеличением N_o (закон Оствальда). Эта зависимость объясняется общими условиями химического равновесия (ср. XLV, ч. 2, 332 сл.). Последнее характеризуется равенством числа распадающихся молекул и числа воссоединяющихся за то же время противоположных ионов. Но для подобного воссоединения необходима встреча («столкновение») двух ионов, а эти столкновения при данном числе их происходят тем реже, чем меньше концентрация ионов при данном общем числе, тогда как скорость диссоциации зависит только от концентрации молекул. Таким образом, при разбавлении раствора скорость диссоциации не меняется, тогда как скорость воссоединения (или «рекомбинации») уменьшается, в результате чего равновесие смещается в сторону увеличения степени диссоциации. Впрочем, новейшие исследования (Дебая и др.) показали, что концентрация раствора влияет не только на степень диссоциации, но и на подвижность «свободных» ионов. Не будучи связаны друг с другом попарно (как в недиссоциированных молекулах), последние оказываются все же частично связанными силами своего электростатического взаимодействия в единый коллектив. Благодаря этим силам, положительные ионы оказываются окруженными преимущественно отрицательными, а отрицательные — преимущественно положительными. Двигаясь в противоположные стороны под действием внешнего электрического поля, они, таким образом, до некоторой степени удерживают друг друга. При уменьшении концентрации раствора это взаимное торможение ионов противоположного знака должно ослабляться, а это ослабление должно влиять на проводимость таким же образом, как и увеличение диссоциации. При малых концентрациях первое обстоятельство является во многих случаях более существенным, нежели второе, в особенности в случае так называемых «сильных» электролитов, то есть растворов с легко диссоциирующими молекулами, которые при больших разбавлениях можно считать нацело диссоциированными.

Прохождение электрического тока через электролит, осуществляясь в виде движения противоположно заряженных частей молекул растворенного вещества в противоположные стороны, должно сопровождаться химическим разложением этого вещества, или, вернее, поскольку диссоциация уже представляет собой разложение — выделением его продуктов на границах электролита. Подобными границами служат погруженные в него металлические пластинки (или проволоки), называемые электродами (рис. 6). Заметим, что положительная пластинка, к которой движутся положительные ионы, называется анодом, а отрицательная — катодом. Доходя до электродов, соответствующие ионы нейтрализуются (путем отдачи электронов в случае отрицательных ионов или захвата их в случае положительных). При этом они либо осаждаются на электродах в виде твердого налета образуемого ими вещества (например, ионы металлов), либо же выделяются около них в виде пузырьков газа, либо же вступают в химическую реакцию с водой, вызывая разложение последней на водород и кислород.

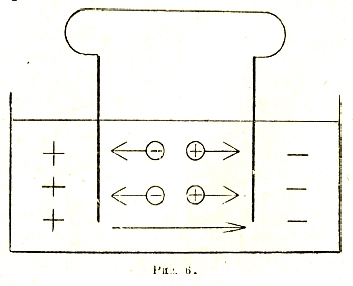
Рис. 6.

Из вышеизложенного ясно, что обычное представление о том, что химическое разложение в электролите «вызывается электрическим током», вдвойне неверно. Во-первых, потому, что оно имеется в скрытой форме (диссоциация) и при отсутствии тока; и во-вторых, потому, что выделение продуктов разложения (ионов) вызывается той же причиной, что и ток, то есть исходящим от электродов электрическим полем, заставляющим двигаться противоположные ионы в противоположные стороны.

В твердом состоянии гетерополярные вещества, образующие при растворении в воде электролиты, обычно рассматриваются как изоляторы. В действительности, однако, они также обладают некоторой, хотя при обычных условиях и весьма слабой, проводимостью, очень быстро, впрочем, возрастающей с повышением температуры. Это обстоятельство объясняется тем, что диссоциация гетерополярных частиц на ионы, поскольку она вызывается тепловым движением, должна иметь место и в твердых телах, образованных этими частицами. Необходимо, впрочем, иметь в виду, что во многих случаях сочленение гетерополярных молекул в кристаллическое тело сопровождается полной «коллективизацией» всех ионов. Так, например, в кристалле каменной соли положительные ионы натрия и отрицательные ионы хлора располагаются в шахматном порядке, так что каждый из них оказывается непосредственно связанным с шестью окружающими его ионами противоположного знака. В подобных случаях, поскольку понятие парной молекулы утрачивает всякий смысл, «диссоциация» ионов сводится к отрыву их от своего нормального положения и переходу к «бродячему образу жизни» между закрепленными (до поры до времени) ионами. Это бродяжничание диссоциированных ионов происходит очень медленно и притом одинаково по всем направлениям при отсутствии внешних сил или же преимущественно в направлении их, если они имеются налицо. Таким образом, помещая между двумя металлическими электродами пластинку «изолирующего» вещества, мы все же получаем слабый ток, обусловленный движением диссоциированных ионов к электродам. Этот ток, так же как и ток в водном растворе рассматриваемого вещества, сопровождается «электролизом», то есть выделением одного из продуктов разложения на соответствующем электроде. Законы этого электролиза в обоих случаях совершенно одинаковы: количество разложившегося вещества оказывается пропорциональным количеству прошедшего электричества, а одному и тому же количеству электричества соответствуют химически эквивалентные количества разных ионов (законы Фарадея).

Необходимо, впрочем, заметить, что в случае большинства кристаллов (так же как и у металлов) перенос электричества осуществляется лишь частицами одного только сорта, обычно положительными ионами (то есть как раз теми частицами, которые в случае металлов остаются неподвижными). Впрочем, при достаточно высоких температурах в проведении тока начинают принимать участие ионы обоих знаков. В некоторых кристаллах, обладающих так называемой «смешанной» проводимостью, в ней участвуют также и «свободные» электроны; в этом случае наряду с обычной диссоциацией имеет место ионизация атомов путем отделения от них электронов, переходящих к бродячему образу жизни. В отличие от металлов, где все атомы являются ионизированными, здесь мы имеем дело с частичной ионизацией, степень которой, так же как и в случае обычной диссоциации, очень сильно зависит от температуры. Зависимость эта выражается формулой вида

где А и В постоянные, а σ — электропроводность (которая, впрочем, является мерой не только числа, но и подвижности соответствующих частиц).

Электропроводность не является исключительным свойством перечисленных выше веществ. В большей или меньшей мере ею обладают все «изоляторы». Во многих случаях она обусловливается, главным образом, содержащимися в них ионными примесями. Однако, и абсолютно чистые диэлектрики обладают некоторой хотя и весьма слабой, проводимостью, причем зависимость ее от температуры выражается той же формулой (6). В тех случаях, когда эта проводимость имеет чисто электронный характер¹) и достигает значительной величины уже при обычных температурах, как, например, в случае угля, селена и других веществ, тело называется не диэлектриком, а полупроводником. Как видно отсюда, различие между диэлектриками и полупроводниками имеет весьма относительный характер, завися всецело от выбора «нормальной» температуры: при достаточно высокой температуре большинство диэлектриков становится полупроводниками, и, наоборот, при достаточно низкой температуре всякий полупроводник становится изолятором. Таким образом, в этом отношении мы имеем существенную разницу не между полупроводниками и диэлектриками, а между полупроводниками и металлами, проводимость которых с понижением температуры не понижается, но, наоборот, увеличивается. Это различие объясняется тем, что в случае металлов число бродячих электронов, будучи равно (приблизительно) числу атомов, не зависит от температуры, которая влияет лишь на их подвижность, между тем, как в случае полупроводников температурой определяется самое число этих электронов. Любопытно также отметить то обстоятельство, что в то время как подвижность ионов (обусловливающих перенос электричества в жидких и твердых электролитах) с понижением температуры уменьшается (благодаря увеличению вязкости), подвижность бродячих электронов в металлах, а равным образом, по-видимому, и в полупроводниках, при этом увеличивается. Эта особенность «свободных» электронов объясняется тем, что в своих странствованиях они не задерживаются у отдельных атомов, но непрерывно переходят от одного атома к соседнему. Неправильности в расположении атомов, вызываемые их тепловым движением, лишь затрудняют этот переход.

¹) То есть обусловливается исключительно оторвавшимися от отдельных атомов электронами.

Различие между металлическими проводниками и диэлектриками имеет, впрочем, с принципиальной точки зрения также относительный характер, не по отношению к температуре, но по отношению к давлению. Как уже было отмечено выше, при достаточной близости между атомами любого вещества, электроны, образующие их наружную оболочку, утратили бы постоянную связь с определенными атомами и превратились бы в «бродяг». Необходимые для такого сближения давления в случае неметаллических веществ столь велики, что они реализуются, по всей вероятности, только в недрах небесных тел под влиянием сил тяготения. Идя в противоположном направлении — увеличения расстояния между атомами и молекулами — мы приходим к газам, являющимся изоляторами как в случае неметаллических, так и в случае металлических веществ.

При отсутствии полной ионизации, обусловленной сцеплением соседних атомов, то есть давлением (внешним или «внутренним»), мы имеем, однако, в металлических парах и других газах чрезвычайно слабую ионизацию, обусловленную тепловым движением. В этом случае оторвавшиеся от атомов электроны являются свободными в полном смысле слова, но зато количество их при обычных температурах столь ничтожно (1 на 10²³ и даже более атомов), что зависящую от них проводимость можно практически не принимать в расчет. Иные условия имеют место, конечно, в газовой атмосфере Солнца и других звезд с их чрезвычайно высокой температурой, а тем более в недрах этих тел, где к температуре, как фактору ионизации, присоединяется высокое давление.

§ 3. Электрический разряд (пробой). При не очень сильных электрических полях диэлектрики, так же как и металлы, подчиняются закону Ома, то есть, другими словами, сохраняют постоянную электропроводность. Однако, при усилении поля за известные пределы последняя начинает чрезвычайно быстро возрастать, так что диэлектрики фактически превращаются в проводники. Обычно это превращение наступает более или менее внезапно и сопровождается ярким свечением (электрическая искра); в твердых и жидких диэлектриках оно связано с сильным нагреванием, вызывающим проплавление и механическое разрушение первых и вскипание вторых. Совокупность этих явлений называется электрическим разрядом, или пробоем. Электрический пробой изоляторов весьма аналогичен механическому разрыву твердых тел под влиянием достаточно большого растягивающего усилия; при этом механическому «пределу прочности» соответствует «пробивное напряжение» Е₀, достижение или превышение которого вызывает пробой диэлектрика. В технике высоких напряжений, связанной с применением изолирующих материалов, эта величина играет такую же роль, как предел прочности в строительной технике. Заметим, что в случае обычно применяемых твердых и жидких изоляторов (стекло, фарфор, масло) пробивное напряжение составляет несколько тысяч абсолютных электростатических единиц на см. В случае газов оно бывает значительно меньше; так, например, для воздуха при нормальном давлении оно равно примерно 100 (то есть 30 000 вольт на см). Сущность пробоя, как уже было отмечено в начале этого параграфа, заключается в резком повышении электропроводности при приближении электрического поля к некоторой критической величине Е₀. Это увеличение электропроводности должно, таким образом, обусловливаться непосредственно или косвенно самим полем. Поскольку электропроводность диэлектрика определяется степенью его ионизации и подвижностью ионов (или электронов), действие поля должно заключаться в увеличении этих факторов или, по крайней мере, одного из них. Напомним для сравнения, что в области справедливости закона Ома они оказываются совершенно независимыми от присутствия поля: последнее не вызывает ионизации, но лишь подхватывает уже «готовые» подвижные заряды, сообщая им скорость, пропорциональную своей напряженности; напомним также, что эта пропорциональность означает пропорциональность между скоростью движения и силой трения (торможения), — пропорциональность, которая должна иметь место лишь при достаточно малых скоростях.

Наиболее изучено явление пробоя в случае газов, где оно обычно известно под именем электрического разряда (см. разряд электричества в газах). Как показал Таунсенд, действие поля сводится в этом случае главным образом к увеличению степени ионизации путем столкновения гонимых полем электронов и ионов с нейтральными частицами (атомами или молекулами). Для того, чтобы подобные столкновения могли привести к ионизации, необходимо, чтобы ударяющая частица имела достаточно большую кинетическую энергию, равную или большую так называемой ионизационной, энергии W₀, то есть той энергии, которую нужно затратить для ионизации нейтральной частицы (путем расщепления ее на положительный ион и электрон или на два противоположных иона). В случае слабых электрических полей кинетическая энергия W, накопляемая электронами или ионами от одного столкновения до следующего, оказывается недостаточной для ионизации ударяемых частиц; она передается им в том же самом виде, то есть в виде кинетической энергии поступательного движения, проявляясь в нагревании газа (Джаулево тепло). Если же электрическая сила, действующая на электрон или ион, столь велика, что за время «свободного пробега», то есть от одного столкновения до следующего, он приобретает кинетическую энергию, большую или равную ионизационной энергии, то столкновение его с нейтральной частицей может сопровождаться в определенном проценте случаев ионизацией последней. Продукты этой ионизации тотчас же подхватываются электрическим полем и в свою очередь ионизуют при столкновениях новые частицы. Таким образом, число ионов и электронов непрерывно, лавинообразно возрастает по мере их движения, а вместе с ним возрастает и сила тока, создаваемого данным электрическим полем.

Впрочем, в ограниченном объеме газа это возрастание силы тока может происходить лишь до тех пор, пока «ионная лавина» не докатилась до электродов, то есть в течение очень короткого времени после включения электрического поля. Затем весьма быстро устанавливается «стационарный режим», при котором число новообразуемых при столкновениях электронов и ионов равно числу электронов и ионов, доходящих за то же самое время до электродов, где они так или иначе «выходят в тираж»; кроме того, необходимо принять в расчет электроны и ионы, взаимно нейтрализующиеся путем воссоединения (рекомбинации) в объеме газа. Таким образом, каждой величине электрического поля Е соответствует определенное стационарное значение силы или плотности тока j (Е). То значение Е, при котором эта зависимость начинает сказываться очень резко (в смысле возрастания), и представляет собой величину пробивного напряжения (или напряженности). Это значение, по существу своему не поддающееся точному определению, лежит обычно очень близко к тому начальному значению Е₀, при котором начинается ионизация столкновениями и которое может быть легко определено из условия, необходимого для этой ионизации, то есть из равенства W = W₀, где W₀ — ионизационная энергия, а W — кинетическая энергия, приобретаемая электроном или ионом между двумя столкновениями.

Эта энергия должна, очевидно, равняться работе электрической силы еЕ, действующей на рассматриваемую частицу, на длине l ее свободного пробега. Мы получаем, таким образом, условие

которое может служить для определения пробивного напряжения в газе.

Так как длина свободного пробега частиц газа обратно пропорциональна его плотности¹), то отсюда следует, что пробивное напряжение должно быть прямо пропорционально плотности или, что то же самое (при данной температуре), — давлению газа.

¹) Следует, впрочем, отметить, что соотношение справедливо лишь при не слишком больших скоростях.

Это соотношение между пробивным напряжением и давлением в точности подтверждается на опыте. В частности, в сильно разреженных разах «электрический пробой» начинается при сравнительно очень слабых полях; в этом случае вместо пробоя говорят обычно об электрическом разряде — «тихом» или «тлеющем» (в виду сопровождающего его свечения).

В предыдущем мы совершенно не касались вопроса о происхождении и количестве тех электронов или ионов, которые являются зачинщиками процесса ударной ионизации. Вопрос этот не имеет существенного значения, подобно тому, как не имеет существенного значения при исследовании процесса взрыва порохового склада вопрос о происхождении искры, его вызвавшей. Заметим лишь, что «первичная» ионизация газа при обычных температурах обусловливается, главным образом, не тепловым движением, а действием особых ионизирующих лучей, отчасти испускаемых радиоактивными веществами, находящимися в почве и в воздухе, отчасти же приходящих из окружающего земной шар пространства (космические лучи). Если эту начальную ионизацию искусственно увеличить, например, действием лучей радия на находящийся в разрядной трубке газ, то наблюдается зависимость силы тока от напряженности поля, изображенная на рис. 7. Здесь область ОА соответствует применимости закона Ома; далее, между А и В ток достигает так называемого «насыщения», то есть максимальной величины, совместимой с данными условиями; он характеризуется тем, что все ионы, непрерывно образующиеся в газе благодаря действию лучей, не успев соединиться друг с другом, относятся полем к электродам. В точке В, где кривая круто заворачивает вверх, начинается ударная ионизация, то есть пробой или разряд.

Необходимо отметить, что зачинщиками его являются именно электроны, а не ионы. Это обстоятельство объясняется обычно (Таунсенд) тем, что электроны, благодаря малости их геометрических размеров (по сравнению с ионами их можно трактовать как точки), обладают значительно большим свободным пробегом, а по тому, согласно формуле (7), могут вызывать ионизацию столкновениями при значительно более слабом поле, нежели ионы. Еще, однако, большее значение, чем размеры, имеет относительная легкость электронов, то есть малость их массы по сравнению с массой ионов, — в особенности в тех случаях, когда электрический разряд вызывается очень сильными полями. А именно, в то время, как массивные ионы лишь начинают разгоняться электрическим полем, легкие электроны успевают не только разогнаться, но и проионизовать большое число атомов, многократно увеличив, таким образом, свою численность. Итак, в начальной фазе всякого электрического разряда в газообразных телах участвуют практически одни только электроны.

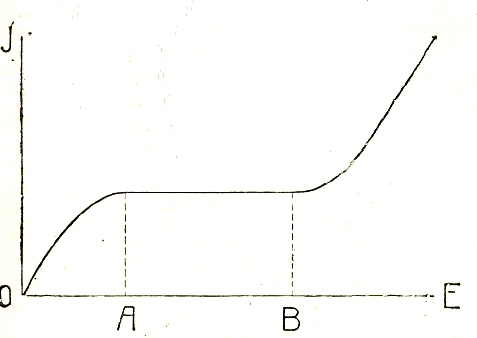
Рис. 7.

Это обстоятельство дает, между прочим, ключ к уяснению формы грозовых разрядов, то есть молнии (Симпсон). Молния (см. XXIX, 221/22) не вспыхивает сразу (как это нам кажется), но представляет собой электрический разряд, который, возникнув в некоторой маленькой области, где электрическое поле достигло пробивного напряжения, быстро растет в сторону, противоположную направлению движения электронов. Это объясняется тем, что последние при своем движении обнажают положительные ионы, от которых они оторвались, и нейтрализуют положительные ионы, находящиеся перед ними: в результате — максимум электрического напряжения, а вместе с ним и область разряда перемещается в тыльную сторону.

Это перемещение сопровождается обычно разветвлением, столь характерным для формы молний. Различные соображения, а также лабораторные опыты показывают, что подобное разветвление пути электрического разряда происходит всегда в сторону от положительного полюса к отрицательному, то есть в сторону, обратную движению электронов.

В сильно разреженных газах оказывается возможным исследовать разряд при напряжениях, значительно превышающих пробивное. Наиболее существенной чертой подобного разряда является образование около катода K «темного пространства» KВ, за которым следует примыкающее к аноду А «положительное свечение» обычного для разряда в данном газе типа. При напряжениях, близких к пробивному, это свечение заполняет все пространство между электродами. По мере увеличения напряжения оно все более и более отодвигается от катода до тех пор, пока, наконец, катодное «темное пространство» не заполнит всей трубки (ср. разряд электричества в газах, XXXV, 514/16). При этом стенки последней начинают светиться зеленоватым светом; эти явления были исследованы еще Круксом, который показал, что свечение стекла вызывается «катодными лучами», то есть потоком электронов, испускаемых катодом. «Темное пространство» представляет собой область, где они движутся более или менее свободно, не испытывая практически никаких столкновений. Мы не имеем возможности останавливаться на более подробном рассмотрении этих явлений. Заметим лишь, что электроны вылетают не из газа, окружающего катод, но из самого катода, откуда они, по-видимому, непосредственно высасываются чрезвычайно сильным полем, которое создается у его поверхности благодаря скоплению около нее положительных ионов.

В случае твердых и жидких тел наблюдение электрического разряда за пределами пробивного напряжения является практически невозможным или крайне затруднительным. Что касается величины пробивного напряжения, то оно (в противоположность случаю газов) зависит от начальной температуры тела. Необходимо иметь в виду, что прохождение электрического тока сопровождается нагреванием, которое в свою очередь вызывает увеличение электропроводности и, следовательно, силы тока (при данном внешнем поле). Это «саморазогревание» тела при прохождении электрического тока может весьма быстро привести к пробою. Механизм подобного пробоя, называемого «тепловым», сводится к местному проплавлению твердого тела, то есть образованию жидкого хорошо проводящего канала или же к местному испарению жидкости, то есть образованию в ней ряда пузырьков пара в направлении от одного электрода к другому. Соответственно этому, пробивное напряжение жидких изоляторов при приближении их (начальной) температуры к температуре кипения стремится к нулю. В случае твердых изоляторов пробивное напряжение с повышением начальной температуры (до нескольких сот градусов Цельсия) также довольно быстро падает, достигая величины совершенно ничтожной по сравнению с нормальной.

Необходимо отметить, что одним из факторов теплового пробоя, наряду с начальной температурой, является теплоотдача тела, то есть отдача выделяющейся внутри него теплоты в наружное пространство и в особенности к электродам. Чем больше теплоотдача, тем выше должна быть начальная температура, при которой данное электрическое поле может вызвать тепловой пробой.

При средних и низких температурах пробой твердых диэлектриков имеет совершенно иной характер или, вернее, подготовляется совершенно другим механизмом.

А именно, как показали новейшие исследования, дело при этом начинается так же, как и в случае газов, с вырывания электронов либо из металлического электрода в диэлектрике, либо из молекул (или атомов) самого диэлектрика. Заметим, что электронный пробой первого типа может иметь место и в пустоте. При наличии электрического поля достаточной интенсивности (порядка 100 тысяч вольт на см), стремящегося вырвать электроны из металла в вакуум, эти электроны, обычно прочно связанные с металлом, начинают на самом деле вырываться наружу и притом в количестве, чрезвычайно быстро возрастающем с увеличением напряженности поля Е (а именно, пропорционально выражению

,

где Е₀ — некоторое характерное для металла поле порядка миллиона вольт на см). Это явление, называемое обычно «холодной электронной эмиссией» (в отличие от термоэлектронной эмиссии, вызываемой высокой температурой), представляет собой по существу не что иное, как «пробой вакуума». Последний представляет собой наилучший изолятор лишь в том смысле, что электроны не могут вырываться из него самого. Если вакуум заменить диэлектриком, то, наряду с совершенно аналогичным процессом срыва электронов из металлического электрода (служащего катодом) в диэлектрик, может иметь место — вероятно при еще больших интенсивностях электрического поля — вырывание электронов из частиц диэлектрика. Эти «первичные» электроны, разгоняясь под действием электрического поля, могут в дальнейшем вырывать из атомов новые электроны (путем соударения, то есть так же, как это имеет место в газах). Впрочем, независимость напряженности поля, способного пробить диэлектрик, от толщины последнего, свидетельствует о том, что эта «ударная» ионизация если и существует, то, во всяком случае, не играет существенной роли. Срыв электронов полем является, вероятно, лишь начальной стадией пробоя; вслед за электронами поле приводит в движение и ионы, причем дальнейшее усиление тока, вероятно, осуществляется путем саморазогревания.

При пробое жидких диэлектриков существенную роль играет, по-видимому, образование или выделение пузырьков воздуха или какого-нибудь другого газа, поглощенного в жидкости. Эти пузырьки, вытягиваясь в направлении поля и сливаясь друг с другом, образуют сплошной газовый путь, который пробивается легче, чем окружающая жидкость. Следует, впрочем, заметить, что вопрос о механизме пробоя жидкостей и твердых тел в настоящее время далеко еще не вполне выяснен.

§ 4. Контактные электродвижущие силы; индукционные электростатические машины; гальванические токи; аккумуляторы. В предыдущем мы оставляли в стороне вопрос о происхождении тех электрических или, как их обычно называют, «электродвижущих» сил, которыми вызываются электрические токи. Основным источником этих сил является (помимо электромагнитной индукции, которая будет рассмотрена в следующей главе) противоположная электризация разнородных тел при соприкосновении их друг с другом. При этом в случае проводников как «первого класса», то есть металлов, так и «второго класса», то есть электролитов, для электризации оказывается достаточным простое соприкосновение без трения, которое обычно является необходимым в случае диэлектриков. Заметим, что, исходя из некоторой хотя бы даже чрезвычайно слабой электризации, получаемой путем соприкосновения («контакта»), можно далее, пользуясь принципом электростатической индукции (гл. I, § 2), получить сколь угодно большое количество противоположных электричеств. На этом принципе в комбинации с так называемым принципом самовозбуждения (который применяется и в связи с электромагнитной индукцией) основаны различные электростатические машины.

Не останавливаясь на описании их устройства, заметим лишь, что действие их заключается в непрерывном отделении друг от друга противоположных зарядов ± е’, полученных путем индукции с помощью ранее имевшихся зарядов ± е, и непрерывном прибавлении первых к последним (положительного к положительному, отрицательного к отрицательному). При разделении разноименных зарядов (в первом акте), так же как и при соединении одноименных (во втором), приходится преодолевать электрические силы (притяжения или отталкивания), то есть, следовательно, совершать работу за счет энергии некоторого механического источника, переводя эту механическую энергию в электрическую энергию, накопляемую машиной. Это накопление происходит до тех пор, пока электрическое поле между ее «полюсами», то есть теми местами, где скопляются противоположные заряды, не оказывается достаточным для пробоя окружающего диэлектрика (воздуха), причем электрическая энергия превращается в тепловую. Если соединить полюса машины проводником, то в последнем получается непрерывный электрический ток, обычно чрезвычайно малой силы, в виду незначительности тех количеств электричества, которые могут быть получены (разделены) электростатическим путем. При этом, конечно, остается весьма малой и разность потенциалов между полюсами машины, определяющая электрическое поле в соединяющем их проводнике, — тем меньшей, чем больше электропроводность последнего.

Несравненно более сильные токи могут быть получены без применения механической работы за счет химической энергии путем соединения нескольких разнородных проводников (среди которых при этом непременно должны присутствовать электролиты, см. ниже) в замкнутую цепь. Происхождение подобных токов, называемых гальваническими (см. гальванизм), станет нам понятным, если мы рассмотрим внимательно явления, происходящие при контакте двух разнородных проводников. Явления эти сводятся с внешней стороны к противоположной их электризации, то есть к переходу некоторого электрического заряда определенного знака с одного проводника на другой. Заряд этот переходит, конечно, не сам по себе, но переносится материальными частицами — электронами или ионами, — которые устремляются от одного проводника к другому вследствие каких-то сил, действующих на них в пограничном слое. Каковы бы ни были эти силы, они, однако, скоро уравновешиваются электрическими силами, появляющимися в этом слое, вследствие противоположной электризации соприкасающихся в нем проводников. Форма и размеры последних при этом, очевидно, не имеют значения. Мы можем, поэтому, сосредоточить своё внимание на пограничном слое. Здесь мы имеем некоторое электрическое поле Е, действующее на протяжении весьма малого расстояния d. Точное знание того, каким образом это поле распределено в толще слоя, то есть на отрезке d, не имеет существенного значения. Практически существенной величиной является лишь соответствующая ему разность потенциалов, называемая контактной разностью потенциалов, или контактным «скачком» потенциала. Этот скачок потенциала ΔV = V₁ – V₂, равный произведению среднего значения Е на d, представляет собой меру той контактной «электродвижущей силы», которая гонит заряды из одного проводника в другой. Обозначая ее через ϕ₁, ₂ мы можем, следовательно, положить

ϕ₁, ₂ = V₁ – V₂,

причем ϕ₂, ₁ = V₂ – V₁ = - ϕ₁, ₂. Если рассматриваемые проводники не соединены ни с какими другими проводниками, то в состоянии равновесия электрическое поле внутри каждого из них, помимо их контактного слоя, исчезает. Это значит, что потенциал каждого из них принимает постоянную величину, отличную от потенциала соседа. Эти потенциалы мы можем подразумевать под величинами V₁ и V₂ в предыдущей формуле.

То же самое получается и в более сложном случае незамкнутой цепи, составленной из нескольких проводников. Считая потенциал первого звена V₁ заданным (он может быть выбран произвольно), мы получаем для всех последующих звеньев вполне определенные потенциалы, связанные друг с другом соотношениями V₂ – V₁ = ϕ₂, ₁, V₃ – V₂ = ϕ₃, ₂ и т. д. Разность потенциалов между крайними звеньями ϕ, равная алгебраической сумме контактных электродвижущих сил ϕ₂, ₁ + ϕ₃, ₂ +..., зависит, при этом, вообще говоря, от промежуточных звеньев. Это обстоятельство остается справедливым и в частном случае цепи, конечные звенья которой одинаковы. Смыкая их друг с другом, мы не должны иметь скачка потенциала между ними. А между тем, при том распределении потенциала, которое соответствовало разомкнутому состоянию цепи, подобный скачок потенциала должен был бы иметь место. Отсюда следует, что в рассматриваемой нами замкнутой цепи, для которой сумма контактных электродвижущих сил (определяемых как скачки потенциала при обходе цепи в определенном направлении) отлична от нуля, равновесное распределение электрического заряда невозможно. Поскольку замкнутость цепи не может влиять на скачки потенциала между соседними ее звеньями, потенциал внутри каждого из них должен изменяться таким образом, чтобы, обойдя цепь в надлежащем направлении, мы получили ту же самую сумму скачков или, как говорят, ту же самую результирующую электродвижущую силу ϕ, как и в том случае, если эта цепь была разомкнута. Таким образом, в звеньях замкнутой цепи, помимо «поверхностного» электрического поля в контактном слое между соседними звеньями, должно иметься обыкновенное «объемное» электрическое поле, а следовательно и неизменный спутник его — электрический ток.

При невозможности равновесного состояния в замкнутой цепи устанавливается в этом случае стационарное состояние, характеризуемое неизменным (во времени) распределением потенциала, а, следовательно, и тока. Это стационарное распределение, характеризуемое постоянством тока во времени, требует также неизменности силы тока в пространстве, точнее —  одинаковости тока для любого поперечного сечения цепи. При несоблюдении последнего условия в отрезке цепи, ограниченном двумя произвольно взятыми поперечными сечениями, происходило бы непрерывное накопление электричества того или иного знака, что несовместимо с постоянством электрического потенциала во времени.

Таким образом, в случае замкнутой цепи с отличной от нуля результирующей электродвижущей силой ϕ мы получаем постоянный электрический ток, вполне определенной, то есть независящей от выбора поперечного сечения, силы і. Легко видеть, что последняя должна быть прямо пропорциональна первой. Этот результат, обычно известный под именем закона Ома, непосредственно следует из той элементарной формы закона Ома, которая была приведена в § 1 (уравнение 4). Его обычно пишут в виде

где R обозначает коэффициент пропорциональности, называемый сопротивлением, или «омическим сопротивлением» цепи, а V' — V'' означает ту разность потенциалов, которая получилась бы на концах рассматриваемой цепи, если бы ее разомкнули, разорвав одно из звеньев.

Сопротивление R зависит от удельного сопротивления каждого из звеньев цепи ρ = 1/σ также, а также, конечно, от его размеров и формы. Контактные слои не играют при этом никакой роли, обусловливая лишь те слагаемые, из которых составляется электродвижущая сила. Считая, что в каждом из этих слоев ток имеет направление, перпендикулярное к ограничивающим его параллельным поверхностям, мы можем трактовать эти поверхности как эквипотенциальные и говорить об определенной разности потенциалов на «концах» каждого звена цепи. Обозначая эту разность потенциалов для n-го звена через V_n’ – V_n’’ (где V_n’ представляет собой потенциал на одном конце, а V_n’’ на другом), мы можем положить

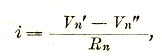
подразумевая под коэффициентом R_n сопротивление проводника, образующего рассматриваемое звено¹).

Отсюда следует

,

или, так как сумма V₁’ – V₁’’ + V₂’ – V₂’’ +... совпадает с суммой скачков потенциала

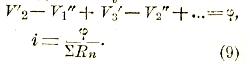
Сравнивая эту формулу с (8), мы видим, что общее сопротивление цепи равно сумме сопротивлений отдельных звеньев

Далее легко показать, что количество тепла Q_n, выделяющегося в n-ом звене за единицу времени, выражается формулой

которую можно также переписать в виде

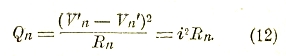
Для этого рассмотрим слой проводника, ограниченный двумя весьма близкими эквипотенциальными поверхностями, и разобьем его на призматические элементы, ограниченные двумя противолежащими участками этих поверхностей. Обозначая площадь одного из этих участков через dS, а расстояние между ними через dl, мы получаем для объема соответствующего элемента выражение dS · dl, а для количества тепла dQ, выделяющегося в нем за единицу времени, согласно формуле (6) § 1,

Принимая во внимание, что произведение Edl = dV представляет собой разность потенциалов на краях слоя, а произведение jdS = di — силу тока, проходящего через рассматриваемый участок его поверхности, мы получаем для теплоты, выделяющейся во всем слое, выражение idV, а следовательно, для всех слоев в n-ом проводнике

¹) R_n зависит только от свойств n-го проводника и остается неизменным при включении его в другую цепь.

Сумма теплоты Qn для всех звеньев цепи представляет собой общее количество теплоты Q, в ней выделяющейся, если пренебречь незначительными тепловыми эффектами, могущими иметь место в контактных слоях (см. следующий параграф). Мы имеем, следовательно, в виду

Эта формула представляет собой обычное выражение закона Джауля.

Заметим, что цепь проводников, способная при замыкании давать электрический ток, то есть обладающая неисчезающей электродвижущей силой, называется, вообще говоря, гальваническим элементом (см. XII, 419 сл.). Как будет показано ниже, подобная цепь не может быть составлена из одних лишь металлических проводников (если только температура их одинакова, см. след. §), но должна содержать хотя бы одно электролитическое звено. Прохождение электрического тока через это звено сопровождается не только выделением тепла, но и выделением продуктов электролиза на его краях (электродах). В результате происходит постепенное изменение контактного скачка потенциала на этих краях и притом в сторону, соответствующую уменьшению электродвижущей силы (э.д.с.), а, следовательно, и силы тока. Это явление называется электролитической поляризацией. Оно представляет собой непосредственное следствие того общего принципа, согласно которому всякая система, будучи предоставлена самой себе, постепенно приходит к состоянию равновесия, если последнее первоначально отсутствовало, как это имеет место в случае замкнутой системы проводов с неисчезающей электродвижущей силой. Таким образом, электрический ток, протекающий в подобной системе, не является вполне стационарным, как это предполагалась выше. В действительности, следуя за изменением электродвижущей силы, он постепенно ослабевает. Заметим, что уменьшение электродвижущей силы гальванического элемента обычно интерпретируется как результат возникновения, вследствие прохождения тока, электродвижущей силы противоположного направления, так называемой поляризационной электродвижущей силы. Последняя появляется при прохождении тока через всякий электролит и может в свою очередь служить источником электрического тока, если электролит выделить из цепи и соединить электроды металлическим проводом. На этом принципе основаны приборы, называемые электрическими аккумуляторами (см. I, 585 сл.). Аккумулятор представляет собой, в сущности, не что иное как гальванический элемент, электродвижущая сила которого создается путем предварительного пропускания электрического тока, питаемого каким-нибудь внешним источником («зарядка»). От хорошего аккумулятора требуется, чтобы при «разрядке» электродвижущая сила оставалась практически постоянной в течение возможно более длительного времени по отношению к общей длительности его действия.

§ 5. Контактные разности потенциалов между металлами; термоэлектрические шоки. Механизм контактной электризации металла и электролита сводится, с одной стороны, к переходу некоторого числа положительных ионов металла в раствор, а с другой — к переходу некоторого числа ионов растворенного вещества на металл. Таким образом, контактный скачок потенциала между металлом и электролитом зависит существенным образом от взаимоотношения между ними.

Проще обстоит дело в случае соприкосновения двух различных металлов друг с другом. В этом случае электризация обусловливается переходом небольшого числа «бродячих» электронов от одного металла к другому, причем контактная разность потенциалов может быть определена непосредственно из условия равенства потенциальной энергии электронов в обоих металлах, после установления равновесия.

Обозначим работу, которую нужно затратить для того, чтобы вырвать один из бродячих электронов из данного металла наружу, через U. Считая эти электроны совершенно свободными до тех пор, пока они находятся внутри металла, мы можем отнести работу U за счет сил, действующих на них в поверхностном слое последнего. Величину — U мы можем при этом трактовать как эффективную потенциальную энергию электрона в металле по отношению к пустоте¹), а величину -U/-е = ϕ (> 0), где -е заряд электрона, как эффективный внутренний потенциал металла при наружном потенциале = 0, или как контактный скачок потенциала при переходе из пустоты в данный металл.

При соприкосновении двух разных металлов электроны будут переходить от того из них, где их потенциальная энергия меньше, то есть где потенциал ϕ больше, к другому, где он меньше, до тех пор пока внутри обоих металлов не установится один и тот же потенциал. Обозначая скачки потенциала у первого и у второго металла соответственно через ϕ₁ и ϕ₂, а дополнительные потенциалы, приобретаемые ими при соприкосновении друг с другом (и обнаруживающиеся не только внутри них, но и во внешнем пространстве), через V₁ и V₂, мы можем записать условие равновесия электронов в виде ϕ₁ + V₁ = ϕ₂ + V₂ или

Таким образом, контактная разность потенциалов между двумя металлами V₁ — V₂, или — что то же самое — электродвижущая сила ϕ₁, ₂, измеряемая этой разностью потенциалов, представляется в виде разности значений двух величин ϕ₁ и ϕ₂, характерных для каждого из металлов в отдельности. Следует подчеркнуть, что это соотношение является отличительным признаком металлических проводников и что оно не имеет места для контактных электродвижущих сил между металлами и электролитами.

Из предыдущего соотношения следует, что в цепи, составленной из нескольких металлов, разность потенциалов между крайними звеньями не зависит от числа и природы промежуточных (закон Вольты).

¹) Слово «эффективный» указывает на то обстоятельство, что энергию U можно было бы считать потенциальной лишь при одинаковости кинетической энергии электронов внутри и вне металла. В действительности последнее условие не соблюдается, ибо внутри металла «свободные» электроны находятся в очень быстром движении, которое не учитывается при обычном определении работы вырывания U.

В самом деле, например, в случае трех металлов мы имеем в качестве условий равновесия цепь равенств V₁ + ϕ₁ = V₂ + ϕ₂ = V₃ + ϕ₃, из которой следует, что V₃ – V₁ = ϕ₁ – ϕ₃ совершенно независимо от ϕ₂.

В частности, при одинаковости конечных звеньев разность потенциалов между ними равна нулю. Соединяя эти звенья друг с другом, мы получим замкнутую цепь с исчезающей электродвижущей силой. Таким образом, в замкнутой цепи, составленной исключительно из металлических проводников, стационарный электрический ток не может иметь места (см., впрочем, ниже).

Мы уже указывали в первой главе (§ 3), что раскаленные металлы испускают электроны. Это испускание представляет собой не что иное, как испарение. Скорость всякого процесса испарения, то есть число n частиц, испаряющихся в единицу времени, зависит от абсолютной температуры испаряющегося тела по формуле

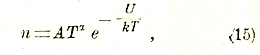
где А, α и U — постоянные. При этом последняя (U) представляет собой «скрытую теплоту испарения», отнесенную к одной частице, то есть, другими словами, работу, которую нужно затратить для отрывания одной частицы от рассматриваемого тела. Показатель α зависит от рода тела, точнее — от теплоемкости его, и близок по порядку величины к 1.

Предыдущая формула, как показал Ричардсон, применима и к электронному испарению, скорость которого может быть легко измерена по силе і соответствующего «термоионного» или, лучше, «термоэлектронного» тока. Заметим, что для предупреждения обратного процесса конденсации электронов, то есть возвращения их в исследуемый металл, их необходимо «отсасывать» внешним электрическим полем. Для этого раскаленный металл присоединяется к отрицательному полюсу гальванического элемента и помещается в непосредственной близости к холодному металлическому электроду, соединенному с положительным полюсом. Воздух из сосуда, содержащего оба электрода, удаляется. Мы получаем, таким образом, простейшую катодную лампу (см. электронная лампа) или электронную трубку с накаливаемым катодом (рис. 9).

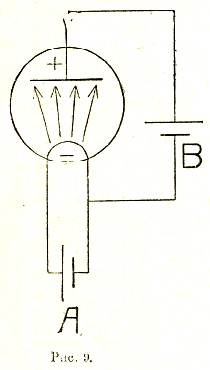
Рис. 9.

Нагревание последнего производится обычно путем пропускания специального тока от вспомогательного элемента (или батареи) А. Таким образом, катод оказывается одновременно включенным в две цепи — «цепь анода», питаемую элементом или батареей  В, и цепь накала. При достаточно большой электродвижущей силе в цепи анода, сила тока в этой цепи достигает предельной величины, при которой всякий испаряющийся из катода электрон попадает на анод. Эта предельная сила тока, зависящая только от температуры катода, равна произведению заряда электрона на число электронов, испаряющихся в единицу времени. Зависимость ее от температуры в точности выражается формулой (15) при α = 2 (что, как показывает термодинамический вывод, соответствует исчезающе малой теплоемкости электронов внутри металла).

Согласно вышеизложенному, энергия испарения электрона U, деленная на его заряд, должна равняться эффективному потенциалу металла ϕ. Опыт показывает, что разность вычисленных таким образом эффективных потенциалов для различных металлов совпадает с непосредственно измеренной контактной разностью потенциалов между ними, в согласии с формулой (14). Следует, впрочем, заметить, что эта формула может считаться вполне точной лишь при абсолютном нуле температуры, ибо только в этом случае равновесие свободных электронов определяется равенством потенциальной энергии их в обоих металлах, то есть равенством нулю электрической силы в переходном слое. При всякой иной температуре оказывается необходимым учитывать давление, производимое электронами. Рассматривая совокупность последних как идеальный газ, подчиняющийся классической статистике Максуэла-Больцмана, мы можем определить величину этого давления известной формулой кинетической теории:

где n обозначает концентрацию, то есть число электронов в единице объема. Если эта концентрация изменяется в направлении от одного металла к другому, то на бесконечно малом отрезке мы получаем разность давлений

В состоянии равновесия эта разность давлений должна уравновешиваться электрической силой, отнесенной к единице объема, которую можно представить в виде произведения -n dW/dx, где W потенциальная энергия одного электрона. Мы имеем, таким образом, уравнение

(ln n обозначает натуральный логарифм n) или, переходя от бесконечно малых изменений W и n на бесконечно малом отрезке dx к конечным изменениям этих величин при переходе от одного металла к другому,

где n₁ и n₂ обозначают концентрации электронов в обоих металлах. Эти концентрации можно рассматривать как характерные для соответствующих металлов постоянные, так как они изменяются совершенно неощутимым образом при переходе небольшого числа электронов от одного металла к другому. Заметим, что формула может быть переписана в виде равенства

определяющего равновесное распределение свободно движущихся частиц в любом внешнем поле, где они имеют потенциальную энергию W.

В рассматриваемом случае мы имеем

Таким образом, мы получаем следующее выражение для контактной разности потенциалов двух разных металлов:

(причем заряд электрона обозначен через -е).

Второй, зависящий от температуры, член в этой формуле чрезвычайно мал по сравнению с первым, так что практически при измерении контактной разности потенциалов он не играет роли.

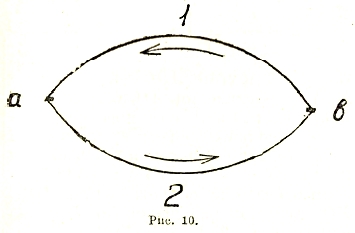
Рис. 10.

Положение, однако, меняется, когда мы имеем дело с замкнутой цепью нескольких металлов, различные сочленения или «спаи» которой имеют разную температуру. В этом случае сумма скачков потенциала при обходе всей цепи в одном определенном направлении, вообще говоря, не исчезает; согласно формуле (16) она должна сводиться к сумме малых «температурных» членов kT/e ln n2/n1

Так, например, в простейшем случае двух металлических проводов 1 и 2, спаи которых а и b (рис. 10) имеют разную температуру Т_а и Т_b, алгебраическая сумма скачков потенциала при обходе цепи в направлении, указанном стрелкой, то есть разность

оказывается равной

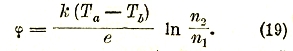
В результате, в подобной замкнутой цепи, при неодинаковости температуры обоих спаев (Т_а и Т_b), получается электрический ток, сила которого пропорциональна результирующему скачку потенциала ϕ. Этот ток называется термоэлектрическим¹), а величина ϕ называется термоэлектродвижущей силой (см. термоэлектричество).

Наличие термоэлектрического тока означает, что «свободные» электроны не могут распределиться равновесным образом при неодинаковости температуры своих спаев. Так как, однако, всякая система, будучи предоставлена самой себе, постепенно переходит в состояние теплового равновесия, то мы должны ожидать, что прохождение термоэлектрического тока должно сопровождаться уменьшением той разности температуры, которой он вызывается, то есть, другими словами, охлаждением более горячего и нагреванием более холодного спая. Поддерживая температуры Т_а и Т_b постоянными, мы должны, следовательно, наблюдать в горячем спае поглощение и в холодном — выделение тепла. Этот эффект был обнаружен на опыте Пельтье и известен под его именем. Его легко вывести непосредственно, рассматривая условия прохождения «свободного» электрона через спай двух металлов. В самом деле, энергия электрона изменяется при этом на величину

Равную согласно формуле (16),

где знак + или – зависит от того или иного направления перехода. Это изменение энергии и обнаруживается в виде выделения тепла — в случае ее уменьшения, или поглощения его — в случае ее увеличения (теплота Пельтье). Следует заметить, что в однородном проводнике, разные части которого имеют разные температуры, также возникают разности электрических потенциалов; однако, они не влияют на результирующую силу тока, вызывая лишь добавочные тепловые эффекты вдоль проводника (эффект Томсона).

Рассмотренный нами случай замкнутой цепи из двух металлических проводов представляет собой простейший пример получения постоянного тока с помощью электродвижущей силы в замкнутом контуре (цепи).

¹) Его не следует смешивать с термоэлектронным током, получающимся при испарении электронов в пустоту.

Следует заметить, что величина и температурная зависимость термоэлектродвижущей силы ϕ оказывается на опыте отличной от теоретической (19). Различие это обусловливается тем, что свободные электроны в металле нельзя трактовать как классический идеальный газ. Более строгая теория, развитая недавно Зоммерфельдом на основе новой статистики Паули-Ферми, приводит к формуле для ϕ, находящейся в полном согласии с опытом.

§ 6. Измерительные приборы и единицы измерения. До сих пор мы совершенно не касались вопроса о методах измерения тех величин, которые встречаются в учении об электрическом токе: силы тока, электродвижущей силы и сопротивления.

Один из простейших методов измерения силы тока основывается на законе Фарадея о пропорциональности этой силы весовому количеству вещества, выделяющегося на электродах в единицу времени при пропускании тока через какой-нибудь электролит. Основанные на этом принципе приборы называются вольтметрами¹).

Для измерения электродвижущих сил служат приборы, называемые электрометрами или вольтметрами. Они основываются либо на измерении электрических сил между двумя проводниками, соединенными с противоположными полюсами разомкнутой цепи, служащей источником электродвижущей силы, либо на измерении силы тока, создаваемой рассматриваемой электродвижущей силой в проводнике с данным предварительно измеренным сопротивлением, либо, наконец, на измерении теплового эффекта в подобном проводнике.

Что касается, наконец, сопротивления, то оно обычно измеряется путем сравнения с каким-нибудь «эталоном», то есть заранее измеренным сопротивлением. Абсолютное определение последнего сводится, в конце концов, к самостоятельному измерению электродвижущей силы и силы тока и вычислению отношения между ними. Наиболее употребительным прибором для относительного измерения сопротивлений служит так называемый мостик Уитстона.

¹) Более распространенными измерителями силы тока являются так называемые гальванометры и амперметры, основанные на магнитных действиях тока (см. XII, 451/64, и электротехника).

Он представляет (рис. 11) собой провод MN, разветвляющийся в точках А и С. Одна ветвь АВС состоит из однородного провода со скользящим контактом В; другая ADC — из измеряемого сопротивления AD и эталонного DC.

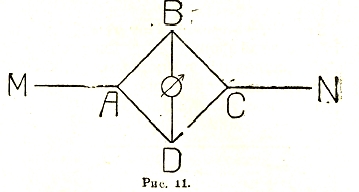
Рис. 11.

Точки В и С соединяются перемычкой, содержащей измеритель силы, тока. Контакт В передвигают до тех пор, пока ток в BD не исчезает. При этом отношение сопротивлений AD и DC должно равняться отношению сопротивлений АВ и ВС, которое непосредственно равно отношению длины АВ к длине ВС.

Предыдущий результат непосредственно вытекает из простых соотношений (так называемых законов Кирхгофа), характеризующих распределение тока, и потенциала в разветвленной сети линейных проводов. Это соотношение сводится к тому, что сумма токов, притекающих по разным проводам к точке, где они встречаются, равна нулю и что разность потенциалов при обходе вдоль замкнутого контура, не содержащего электродвижущих сил, равна нулю.

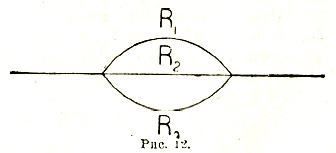
Рис. 12.

С помощью приведенных соотношений нетрудно далее показать, что сопротивление R нескольких последовательно включенных проводов равно сумме их сопротивлений: R₁ + R₂ + … тогда как при «параллельном» их включении путем разветвления (рис. 12) складываются не их сопротивления, а обратные величины, то есть проводимости:

Путем последовательного или параллельного соединения нескольких разомкнутых гальванических цепей получаются гальванические (или аккумуляторные) батареи (см. XII, 439/41). Не останавливаясь подробнее на этих не имеющих принципиального значения вопросах, мы рассмотрим в заключение вопрос о тех единицах, которыми пользуются на практике для измерения электродвижущих сил токов и сопротивлений (см. XII, прил. единицы измерений, 6/8). Практической единицей электродвижущей силы, или разности потенциалов, служит вольт, равный 1/300 электростатической единицы разности потенциалов. Соответственным образом уменьшается и единица напряженности электрического поля, определяемая как градиент потенциала в 1 вольт на см. Практической единицей электрического заряда и силы тока служат соответственно кулон и ампер, равные 3.10⁹ электростатических единиц заряда и силы тока. Практическая единица сопротивления определяется как такое сопротивление, при котором электродвижущая сила в 1 вольт дает ток в 1 ампер. Эта единица сопротивления называется омом. Заметим, что контактные электродвижущие силы имеют обычно порядок 1 вольта.

Удельное сопротивление ρ разных металлов (равное обратной величине их электропроводности σ) колеблется обычно при нормальных температурах в пределах от одной стотысячной до одной миллионной ома. Сопротивление R металлического стержня с длиной l и сечением S может быть вычислено из удельного сопротивления ρ по формуле

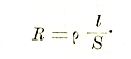
Таким образом, в случае провода с сечением в 1 кв. мм = 10^-2 кв. см мы получим сопротивление в 1 ом при длине порядка 10-100 метров. В случае ртути, имеющей исключительно большое сопротивление, эта длина близка к 1 метру. Громадность тех количеств электричества, которые перемещаются в металлах при прохождении электрических токов под влиянием весьма незначительных электрических сил, объясняется тем, что при этом используются все скрытые в проводах резервы подвижных электрических зарядов, между тем как в электростатических явлениях обнаруживаются лишь ничтожные части этих резервов.

В непосредственной связи с практическими единицами заряда, тока и потенциала находятся практические единицы работы и мощности. Практическая единица работы называется джоулем; ее можно определить, как работу, совершаемую при прохождении зарядом в 1 кулон падения потенциала в 1 вольт. Другими словами, это есть работа, совершаемая в 1 секунду электродвижущей силой в 1 вольт в цепи, по которой течет ток в 1 ампер. Эта работа эквивалентна, количеству теплоты, равному 0,24 малых калорий. Мощность, при которой в 1 секунду совершается работа в 1 джоуль, называется ваттом. На практике обычно пользуются в 1000 раз большей единицей, называемой киловаттом и близкой к механической единице мощности — лошадиной силе. Впрочем, следует заметить, что приставки кило-, милли- и т. д. применяются не только к ватту, но равным образом и к другим электрическим единицам для обозначения в 1000 раз больших или в 1000 раз меньших единиц (например, 1 киловольт обозначает 1000 вольт, один миллиампер — 0,001 ампера). На практике в качестве единицы энергии часто потребляется так называемый «ватт-час», то есть энергия, выделяющаяся в течение часа при мощности в 1 ватт. Эта энергия равна 3 600 джоулей.

Наконец, следует упомянуть, что практической единицей емкости служит емкость проводника, который при заряде в 1 кулон получает потенциал в 1 вольт. Эта единица, равная 9.10¹¹ см, называется фарадой. Обычно емкость измеряется в микрофарадах (= 9.10⁵ см).