Электричество. Глава III. Электромагнитные явления и магнетизм

Электричество. Глава III. Электромагнитные явления и магнетизм. § 1. Взаимодействие движущихся электрических зарядов (электрокинетические действия). Взаимодействие заряженных частиц не ограничивается кулоновскими силами притяжения и отталкивания. В том случае, когда эти частицы движутся, к электрическим силам, зависящим только от их положения, присоединяются так называемые электрокинетические силы, пропорциональные электрическим количествам движения, то есть произведению заряда каждой частицы на ее скорость. От положения частиц электрокинетические силы зависят совершенно так же, как и электростатические, то есть они убывают с расстоянием обратно пропорционально его квадрату. Кроме того, однако, они зависят определенным образом от направления движения (скорости) каждой из двух взаимодействующих частиц, то есть от углов, образуемых их скоростями (электрическими количествами движения) друг с другом и с соединяющей их прямой.

Таким образом, электрокинетическая сила f₁₂, действующая со стороны одной частицы (1) на другую (2), может быть выражена формулой

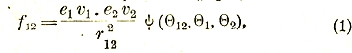
где e₁ и v₁ — заряд и скорость движения первой частицы, е₂ и v₂ — те же величины для второй, r₁₂ — их взаимное расстояние¹), а ϕ — некоторая функция от угла ϴ₁₂ между векторами  и  ,угла ϴ₁ между

 и ϴ₂ между.

Формула (1) характеризует — и то весьма неполным образом (поскольку функция ϕ остается неопределенной) — лишь величину силы. Что касается ее направления, то оно определяется довольно сложным образом через направления векторов. А именно, сила оказывается перпендикулярной к вектору то есть к направлению движения той частицы, на которую она действует, и лежит в плоскости, содержащей векторы

 и то есть скорость частицы, от которой она исходит, и расстояние между обеими частицами.

¹) Которое мы будем представлять себе в виде вектора, проведенного от 1-ой частицы ко второй.

В простейшем случае, когда последние движутся совместно, то есть с одинаковой по величине и направлению скоростью, и притом таким образом, что соединяющая их прямая перпендикулярна к направлению их движения (рис. 13), электрокинетические силы с которыми они действуют друг на друга, приобретают характер обычного кулоновского притяжения или отталкивания,

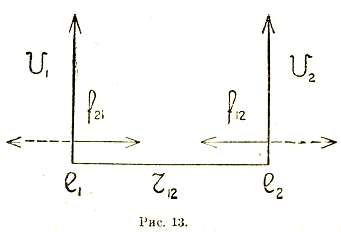
Рис. 13.

направленного вдоль прямой r₁₂ и равного

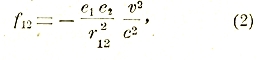
где 1/с² — коэффициент пропорциональности, равный численному значению углового множителя ϕ в (1) при ϴ₁₂ = 0 и ϴ₁ = ϴ₂ = 90°.

В случае одноименных зарядов сила (2) имеет характер взаимного притяжения, а в случае разноименных — характер взаимного отталкивания. Таким образом, в обоих случаях электрокинетическое взаимодействие имеет направление прямо противоположное электростатическому — это обстоятельство выражается отрицательным знаком в формуле (2). Коэффициент с обладает размерностью скорости и может быть определен как такая скорость движения обоих зарядов v = с, при которой электрокинетическое взаимодействие их в точности уравновешивает электростатическое. Опыт показывает, что коэффициент с равен 3 · 10¹⁰ (см/сек.), то есть совпадает со скоростью распространения света в пустоте. Значение этого совпадения станет нам яснее в дальнейшем. Здесь мы отметим лишь то обстоятельство, что на опыте скорость движения материальных частиц никогда не достигает «критической» скорости с. Поэтому, фактически, электрокинетическая сила (2) может лишь ослаблять электростатическую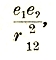 но не уравновешивать, а тем более перевешивать ее.

Далее, необходимо подчеркнуть, что как в формуле (2), так и в более общей формуле (1), под скоростями подразумеваются скорости обеих частиц по отношению к наблюдателю, то есть по отношению к некоторой системе координат, принимаемой за неподвижную. Выбор этой системы координат остается в значительной мере произвольным, что связано с относительным характером движения и, в частности, скорости прямолинейного и равномерного движения (см. ниже гл. IV).

Наконец, нужно отметить тот факт, что электрокинетические силы, в противоположность электростатическим, не удовлетворяют принципу равенства и противоположности действия и противодействия. Это видно уже из того обстоятельства, что скорости двух действующих друг на друга частиц входят в выражение электрокинетической силы, испытываемой каждой из них, несимметрическим образом. Если, однако, мы возьмем слагающие обеих сил

 параллельные прямой, то они оказываются равными и противоположными друг другу и могут быть выражены простой формулой

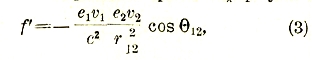
которая обращается в (2) при v₁ = v₂ и ϴ₁₂ = 0.

Эта формула характеризует главную часть электрокинетического взаимодействия, то есть часть, сводящуюся к взаимному притяжению или отталкиванию. Заметим, что эта часть равна электростатическому взаимодействию, умноженному на –v₁v₂/c² cosϴ₁₂. В случае, если скорости v₁ и v₂ образуют между собою острый угол, этот множитель отрицателен (силы того и другого рода имеют противоположное направление); при тупом угле ϴ₁₂ оба взаимодействия направлены одинаковым образом. В обоих случаях электрокинетическое притяжение или отталкивание остается меньше электростатического.

Подобно тому, как электростатическому взаимодействию двух заряженных частиц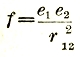 соответствует потенциальная энергия точно так же продольной (параллельной r) части электрокинетического взаимодействия соответствует потенциальная энергия

Что касается поперечной части, то есть тех слагающих сил которые перпендикулярны к расстоянию то, не будучи равными и противоположными, они не могут быть выведены из какой-либо потенциальной функции.

Для более полной и точной характеристики электрокинетических сил вводят вспомогательное понятие магнитного поля или магнитной напряженности¹), аналогичной электрической напряженности которая служит для описания электростатических взаимодействий. При этом сила действующая на заряд 2 со стороны заряда 1, определяется следующим образом.

а) Двигаясь со скоростью в магнитном поле создаваемом зарядом е₁, заряд е₂ испытывает силу, перпендикулярную к векторам и равную

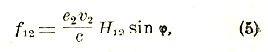
где ϕ — угол между

.

¹) Или напряженности магнитного поля.

По численному своему значению эта сила равна площади параллелограмма, построенного на векторах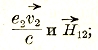 по своему направлению она совпадает с тем из двух направлений, перпендикулярных к плоскости этого параллелограмма, в котором надо смотреть для того, чтобы поворот от вектора к вектору на угол ϕ меньший 180° совпадал бы с направлением вращения стрелок часов; другими словами, сила  направлена в сторону поступательного движения обыкновенного («правого») винта, вращаемого от вектора к вектору .

Так, например, если первый из них направлен вверх, а второй — направо, то сила должна быть направлена вперед.

b) Магнитное поле создаваемое зарядом е₁, движущимся со скоростью на расстоянии  перпендикулярно к векторам и равно

где ϴ — угол между Таким образом, магнитное поле обратно пропорционально квадрату расстояния. Что же касается его направления, то оно совпадает с направлением движения (правого) винта, вращаемого (на угол ϴ < 180°) от вектора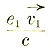 к вектору

Так, например, если первый из них направлен вперед, а второй — направо, то поле должно быть направлено вниз.

Для наглядного изображения магнитного поля пользуются так называемыми магнитными силовыми линиями, которые проводятся согласно тем же принципам, как и в случае поля электрического, то есть так, чтобы направление линии в каждой точке совпадало с направлением поля в этой точке, а густота линий была пропорциональна напряженности поля (см. XXVII, 582'/84'). При этих условиях магнитное поле движущегося точечного заряда может быть представлено в виде системы коаксиальных кругов, то есть кругов с общей осью; последняя проходит через заряд в направлении вектора е и содержит центры кругов, образуемых магнитными силовыми линиями. Направление последних связано с направлением оси по правилу винта: если, следовательно, смотреть на силовые линии в направлении оси, то направление обхода вдоль любой из них совпадает с направлением движения стрелки часов. Так, например, в случае положительного заряда, движущегося вертикально вниз, магнитные силовые линии образуют горизонтальные круги, направление которых для наблюдателя, смотрящего на них сверху, совпадает с направлением движения часовой стрелки. Что касается густоты, силовых линий, то, согласно предыдущему, она должна быть обратно пропорциональна квадрату расстояния от заряда, а при данном расстоянии уменьшаться по мере приближения к направлению оси, обращаясь в нуль вблизи последней.

Закон (5), определяющий действие магнитного поля на движущийся заряд, называется законом Ампера, а закон (6), определяющий магнитное поле, создаваемое движущимся зарядом, называется законом Био-Савара, по имени установивших эти законы французских ученых.

Как видно из предыдущего, понятие магнитного поля, не будучи существенно необходимым для описания электрокинетического взаимодействия, оказывается все же весьма удобным в смысле более простого и точного описания этого взаимодействия. Единица напряженности магнитного поля носит название «гаусса» (в честь немецкого математика Гаусса, впервые разработавшего теорию земного магнетизма, см. ниже). Заметим далее, что при изучении электрокинетического взаимодействия наэлектризованных частиц вместо обычной электростатической единицы электрического заряда вводится в с = 3 · 10¹⁰ раза большая единица, называемая электромагнитной. При этом условии выражение  играющее в случае с электрокинетического взаимодействия роль, аналогичную той, которую заряд е играет в случае взаимодействия электростатического, может быть определено как электрическое количество движения, выраженное в электромагнитных единицах (ибо отношение е/с представляет собой в электромагнитных единицах заряд, равный е электростатических единиц).

§ 2. Взаимодействие электрических токов. Электрокинетическое взаимодействие заряженных частиц обнаруживается на опыте простейшим и наиболее непосредственным образом в виде так называемых «пондермоторных» сил, действующих между замкнутыми металлическими проводниками, по которым текут постоянные электрические токи. В этом случае, поскольку различные элементы рассматриваемых проводников нейтральны, электростатическое взаимодействие между ними исчезает. Что же касается электрокинетического взаимодействия, то в этом отношении элемент объема какого-либо проводника dV, при наличии в нем электрического тока с плотностью ведет себя как заряд с электрическим количеством движения

В случае тонкого «линейного» проводника под dV обычно подразумевается элемент объема, соответствующий весьма малому элементу длины ds. Обозначая поперечное сечение подобного проводника через q, мы имеем dV = qds и, следовательно, jdV = jqds = ids, где i представляет собой силу тока в обычном определении, то есть количество электричества, проходящего в единицу времени через данное или — в виду стационарности тока — через любое сечение рассматриваемого проводника. Таким образом, отрезок ds линейного проводника (проволоки), в котором течет ток силы і, в смысле производимых и испытываемых им электрокинетических действий эквивалентен точечному заряду с электрическим количеством движения ids. Это выражение называется обычно элементом тока. Если, следовательно, измерять силу тока не в электростатических единицах, как это делалось во II главе, а в электромагнитных единицах, то в применении к элементу тока законы Ампера и Био-Савара могут быть выражены формулами

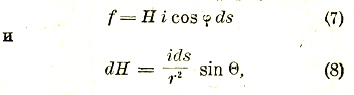
причем направление электрического количества движения определяется в обоих случаях тем направлением отрезка ds, в котором происходит перенос положительного электричества. Поскольку в металлических проводах перенос электричества осуществляется отрицательными электронами, это направление фактически противоположно направлению движения последних.

Из формулы (8) следует, что в центре кругового тока, то есть тока, текущего по окружности радиуса r, магнитная напряженность равна (в виду s = 2πr и ϴ = 90°):

причем вектор направлен в сторону движения (правого) винта, вращаемого в направлении тока.

Несколько более сложное вычисление показывает, что в случае прямолинейного провода очень большой (практически бесконечной) длины, магнитная напряженность обратно пропорциональна расстоянию от провода R и равна

При этом магнитные силовые линии образуют круги, охватывающие провод, который служит их общей осью. В непосредственной близости к линейному проводнику любой формы магнитное поле имеет то же самое строение, как и в случае бесконечного прямолинейного проводника. Вообще же говоря, магнитные силовые линии имеют при этом форму замкнутых колец, охватывающих контур тока (проводник), как показано на рис. 14.

На очень больших расстояниях от (замкнутого) проводника с током, то есть таких расстояниях r, которые очень велики в сравнении с линейными размерами проводника, магнитное поле имеет строение, тождественное со строением электрического поля, создаваемого двумя зарядами равной величины и противоположного знака, расположенными надлежащим образом в той же области, где находится проводник. Совокупность двух подобных зарядов называется электрическим диполем.

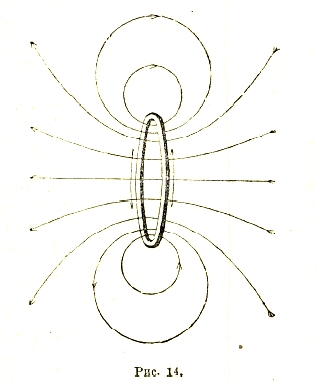
Рис. 14.

Выше (гл. I) мы уже определили момент диполя как вектор, равный произведению отрезка, проведенного от отрицательного заряда к положительному (d), на их численное значение (е). На больших расстояниях от электрического диполя поле его всецело определяется вектором момента

Соответственно этому для характеристики магнитного поля на большом расстоянии от замкнутого тока часто пользуются представлением о магнитном диполе, образованном двумя «магнитными зарядами» или «полюсами» противоположного знака и создающими в отдельности магнитное поле, тождественное с электрическим полем точечного электрического заряда. В действительности подобных полюсов не существует, так что они должны рассматриваться лишь как удобные фикции. Обозначая численное значение полюсов магнитного диполя через т, а вектор, проведенный от отрицательного полюса к положительному, через  мы можем определить произведение  как момент магнитного диполя. Несмотря на фиктивность обоих его сомножителей, этот вектор имеет вполне реальное значение, так как он определяет магнитное поле замкнутого тока (на больших расстояниях) совершенно таким же образом, каким вектор электрического момента определяет поле электрического диполя (также, конечно, лишь на больших расстояниях).

Магнитный момент замкнутого электрического тока может быть представлен в виде произведения двух множителей, имеющих вполне реальное значение. Одним из этих множителей является сила тока i, а другим — некоторый вектор, зависящий от формы и размеров контура (проводника), а также от направления, в котором он обтекается током. В простейшем случае плоского контура этот вектор численно равен его площади S, причем направление его связано с направлением тока по правилу (правого) винта. Таким образом, численное значение магнитного момента электрического тока выражается в этом случае формулой

В случае электрического диполя вектор момента определяет не только производимое им действие (т. е. поле), но и действие, испытываемое им в данном внешнем поле. Действие это сводится, во-первых, к вращательному усилию, стремящемуся ориентировать момент диполя в направлении силовых линий, и, во-вторых, к некоторой силе, стремящейся двигать его в сторону увеличения или уменьшения густоты силовых линий, то есть напряженности поля,— в зависимости от того, образует ли направление последнего острый или тупой угол с направлением момента. При перпендикулярности последнего к полю, движущая сила обращается в нуль, тогда как вращательное усилие достигает максимума, а при параллельности, наоборот, исчезает вращательное усилие, и достигает максимального значения движущая сила. Эти результаты могут быть легко выведены из рассмотрения потенциальной энергии диполя. Обозначая потенциал внешнего электрического поля на отрицательном и на положительном конце диполя соответственно через ϕ₁ и ϕ₂, мы можем представить эту потенциальную энергию в виде

где р = еd — момент диполя, а — проекция электрической напряженности в направлении его оси. Мы получаем, таким образом, U = -pE cosα. В случае магнитного диполя потенциальная энергия выражается аналогичной формулой

где α обозначает угол между векторами

Это выражение можно вывести непосредственно, исходя из формулы (7), определяющей силу, испытываемую элементами тока в данном внешнем магнитном поле, в предположении, что в области, занимаемой контуром тока, это поле остается (приблизительно) однородным, то есть неизменным по величине и направлению; другими словами, предполагается, что линейные размеры тока малы в сравнении с теми расстояниями, на которых происходит изменение поля

Таким образом, эквивалентность подобного «элементарного линейного тока» магнитному диполю имеет место не только по отношению к действию, производимому им, но и к действию, им испытываемому.

Само собой разумеется, что эта эквивалентность имеет место лишь при условии «элементарности» тока, то есть при малости его геометрических размеров в сравнении с расстояниями, для которых определяется создаваемое им поле или на которых заметно изменяется поле, на него действующее. В непосредственной близости к замкнутому току и эквивалентному ему диполю, поля, создаваемые ими, имеют совершенно различное строение. Для того, чтобы обеспечить эквивалентность их в наиболее полной степени, вместо диполя, образованного двумя точечными магнитными полюсами, вводят так называемый двойной магнитный слой или листок. Подобный слой представляет собой бесконечно тонкую лепешку, ограниченную контуром тока, но помимо этого обстоятельства могущую иметь произвольную форму. Одна сторона этой лепешки покрыта отрицательным, а другая положительным магнетизмом таким образом, чтобы произведение поверхностной плотности «магнитного заряда» на толщину слоя равнялось силе тока (что соответствует совпадению магнитного момента слоя и тока). При таких условиях магнитное поле вне слоя в точности совпадает с магнитным полем окаймляющего его тока — вплоть до сколь угодно малых расстояний от отрицательной или положительной поверхности слоя. Магнитные силовые линии, начинаясь на положительной стороне, охватывают контур тока и заканчиваются на отрицательной стороне. Считая их бесконечно близкими и сцепляя оба конца каждой из силовых линий, мы получим в точности картину поля, создаваемого током. Внутри же слоя, то есть в бесконечно тонком промежутке между его поверхностями, магнитное поле меняет свое направление на противоположное и приобретает бесконечно большую напряженность — что, конечно, никакого отношения к действительности не имеет. Исключая, однако, эту область, мы можем считать данный ток совершенно эквивалентным соответствующему двойному магнитному слою как в смысле действий, им производимых, так и в смысле действий, им испытываемых.

Вопрос о взаимодействии двух замкнутых линейных токов может быть решен непосредственно, то есть без введения понятия магнитного поля, при помощи выражения (4) для взаимной потенциальной энергии, соответствующей продольной части электрокинетического взаимодействия (т. е. взаимному притяжению или отталкиванию) двух движущихся зарядов. Заменяя соответствующие последним электрические количества движения элементами токов i₁ds₁ и i₂ds₂, мы получаем

Легко показать, что сумма этих выражений для различных элементов обоих токов представляет собой взаимную потенциальную энергию последних, совпадая с взаимной потенциальной энергией эквивалентных им магнитных листков. Таким образом, поперечные слагающие электрокинетического взаимодействия, не учитываемые выражением (11), выпадают из рассмотрения при суммировании этих взаимодействий для всех элементов замкнутого тока.

Взаимная потенциальная энергия двух замкнутых токов может быть представлена согласно формуле (11) в виде

где L₁₂ — некоторый коэффициент, имеющий размерность длины и зависящий от формы и расположения соответствующих проводников. Этот коэффициент называется коэффициентом взаимной индукции¹) обоих токов (см. ниже). Аналогичным образом, исходя из той же формулы (4), можно определить потенциальную энергию какого-либо замкнутого тока на самого себя. Эта собственная потенциальная энергия тока выражается формулой

где L называется коэффициентом самоиндукции²) данного тока или, вернее, проводника. Эта формула может быть получена из предыдущей, если представить себе рассматриваемый ток расщепленным на множество параллельных бесконечно тонких токовых нитей и если энергию его определить как взаимную потенциальную энергию всех этих нитей друг на друга. Собственная потенциальная энергия тока может, разумеется, проявиться только в том случае, если контур его не твердый (как это предполагалось до сих пор), но способен деформироваться.

¹) Или взаимной индуктивностью.

²) Или собственной индуктивностью.

§ 3. Электромагнитная индукция. В случае неподвижных проводников электрокинетическое взаимодействие проявляется в виде пондермоторных сил, то есть сил, действующих на каждый элемент проводника в поперечном (перпендикулярном к нему) направлении. В том случае, когда рассматриваемый проводник перемещается в данном магнитном поле, создаваемом какими-нибудь другими неподвижными проводниками с постоянными токами, к этим поперечным пондермоторным силам присоединяются продольные электромоторные силы, то есть электрические силы, действующие в продольном направлении и притом в противоположных направлениях на противоположные заряды, содержащиеся в каждом элементе проводника. Происхождение этих продольных сил то же самое, что и поперечных сил: первые определяются поперечной слагающей скорости зарядов, движущихся вместе с проводником, совершенно таким же образом, как вторые обусловливаются продольной слагающей скорости этих зарядов по отношению к проводнику. Однако, внешний эффект тех и других совершенно различен: действуя в поперечном направлении, «пондермоторные» силы стремятся вызвать перемещение проводника как целого, в то время как продольные силы, не действуя на проводник как целое, стремятся вызвать перемещение противоположных зарядов в противоположные стороны, то есть изменить силу тока, образуемого продольным движением этих зарядов.

Представим себе, например, вертикальный проводник длины l, движущийся слева направо со скоростью v в однородном магнитном поле Н, направленном к наблюдателю. При отсутствии в проводнике электрического тока мы можем считать, что каждый из находящихся в нем зарядов е движется направо с той же скоростью v и испытывает силу, перпендикулярную к направлению движения и поля, то есть параллельную длине проводника, и равную согласно формуле (5) ev/с H. В случае е > 0 эта сила должна быть направлена вверх, а в случае е < 0 вниз.

Таким образом, действие магнитного поля на движущийся в нем проводник оказывается в рассматриваемом случае эквивалентным действию продольного (вертикального) электрического поля с напряженностью

Если скорость v образует с полем Н угол ϕ (оставаясь в горизонтальной плоскости), то эквивалентное электрическое поле оказывается равным

Представим себе прямоугольную рамку с двумя вертикальными сторонами с высотой l и двумя горизонтальными с длиной 2а. Если вращать подобную рамку вокруг вертикальной оси, проходящей через середины горизонтальных сторон, то в каждый момент времени противоположные вертикальные стороны будут иметь противоположно направленные скорости, чему соответствует противоположное направление эквивалентных электрических полей (рис. 15).

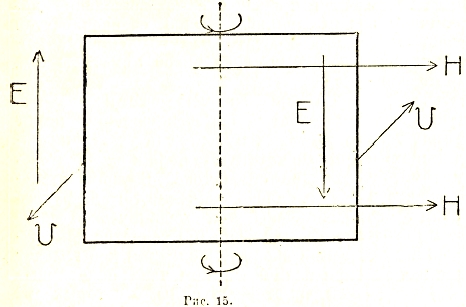
Рис. 15.

В виду замкнутости контура, образуемого рамкой, действие этих полей будет складываться, вызывая электрический ток определенного направления, зависящего от угла, образуемого нормально к рамке, с направлением магнитного поля и от направления вращения.

Описанное нами явление возникновения электродвижущей силы в замкнутом проводнике при движении его в магнитном поле называется электромагнитной индукцией (точнее — оно представляет собой частный случай электромагнитной индукции, см. ниже). Что касается величины индукционной электродвижущей силы, то она может быть определена на основании того же принципа, который служит для определения электродвижущих сил гальванического происхождения, а именно — величиной той разности потенциалов (или суммы подобных разностей), которая необходима для ее компенсации. Если в контуре с длиной l действует электродвижущая сила, эквивалентная электрическому полю Е, то величина этой электродвижущей силы равна Еl. В только что рассмотренном случае вращающейся рамки мы получаем, таким образом, электродвижущую силу V = 2 Еl. Сила вызываемого ею тока может быть определена по формуле і = V/R, где R — общее сопротивление проводника, образующего рамку (с поправкой на самоиндукцию; см. ниже).

Обозначая угловую скорость вращения рамки через ω, мы имеем v = ωа и, следовательно,

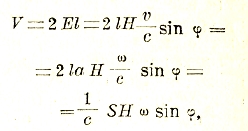
где S = 2 аl — площадь рамки. Так как скорость ω равна быстроте изменения угла ϕ, то есть производной его по времени dϕ/dt, то, принимая во внимание, что sin ϕ dϕ/dt = -d/dt (cos ϕ), мы получаем следующее равенство:

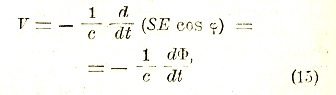
где величина Ф = SН cos ϕ представляет собой так называемый магнитный поток через контур рамки. Изображая магнитное поле при помощи силовых линий, проводимых с таким расчетом, чтобы число их на единицу площади численно равнялось напряженности поля Н, мы можем определить магнитный поток как число магнитных силовых линий, пронизывающих рассматриваемый контур в данном направлении (изменению последнего на противоположное соответствует изменение знака магнитного потока).

Формула (15) может быть установлена в общем случае произвольного движения какого-либо линейного проводника в постоянном магнитном поле более простым, хотя и несколько косвенным образом, основывающимся на том обстоятельстве, что электрокинетическая сила, действующая на движущийся заряд, вследствие своей перпендикулярности к направлению движения не может производить работы. Отсюда следует, что работа электромоторных сил, появляющихся в движущемся проводнике с некоторым током і, должна быть равна по величине и противоположна по знаку работе пондермоторных сил, действующих на него за то же самое время. Но работа электромоторных сил может быть выражена произведением индукционной электродвижущей силы V на силу тока іс (в электростатических единицах) и на время dt. Работа же пондермоторных сил может быть представлена убылью потенциальной энергии этого проводника U' по отношению к источнику магнитного поля (который мы можем представлять себе в виде какого-либо другого неподвижного проводника) за то же время, при неизменной силе тока i. Мы получаем, таким образом, равенство

или

С другой стороны, как мы видели выше, потенциальная энергия U' в случае элементарного тока (то есть проводника малых размеров) выражается формулой (10). Подставляя в нее значение магнитного момента тока μ = iS, мы получаем U' = -iSH cos ϕ, или

Эта формула может быть легко обобщена на случай линейного замкнутого тока произвольных размеров и формы. Считая силу тока постоянной, мы получаем, следовательно,

В рассмотренной нами форме явление электромагнитной индукции представляет собой основной источник электрического тока в технике. Машины, служащие для его получения этим путем, называются динамо-машинами. Обычно динамо-машины (подобно электростатическим машинам) основываются на комбинации принципа электромоторной индукции с принципом самовозбуждения. Последний заключается в том, что ток, индуктированный во вращающемся проводнике (якоре), пропускается (последовательно или параллельно) через неподвижный проводник (обмотку возбуждения), создавая или усиливая, таким образом, индуктирующее магнитное поле. То первичное магнитное поле, которое необходимо в самом начале процесса самовозбуждения динамо-машины, обычно обеспечивается слабым остаточным намагничиванием железных сердечников арматуры (см. ниже).

На первый взгляд может показаться, что путем самовозбуждения могут быть достигнуты сколь угодно интенсивные магнитные поля и сколь угодно большие силы тока. В действительности, однако, значения того и другого ограничены той механической мощностью, которая применяется для вращения якоря. Последний испытывает при наличии в нем тока поперечные пондермоторные силы, о которых мы говорили выше и которые противодействуют вращательному движению, вызывающему индукционный ток.

Пропуская через динамо-машину электрический ток, создаваемый каким-нибудь посторонним источником, можно привести во вращение ее якорь, то есть заставить ее действовать как электромотор. При этом «обращенном» действии динамо-машины в ней индуктируется, однако, обратная электродвижущая сила, то есть электродвижущая сила, противоположная той, которой вызывается ток, чем ограничивается скорость вращения якоря (см. электротехника — электрические машины).

Таким образом, в обоих случаях взаимодействующие факторы находятся в антагонистическом отношении друг к другу, то есть, если фактор А (например, вращение якоря) вызывает В (ток), то фактор В стремится уменьшить А. Этот принцип — применимый, впрочем, не только к электромагнитным явлениям, но и к множеству других явлений физики — называется обычно законом Ленца.

Чрезвычайно общая форма, в которой выражается закон электромагнитной индукции, делает весьма естественным обобщение его на тот случай, когда изменение магнитного потока Ф, определяющее согласно формуле (17) индукционную электродвижущую силу, вызывается не движением данного проводника, а изменением магнитного поля, в котором находится неподвижный проводник, или же комбинацией того и другого фактора. Представим себе, например, два замкнутых линейных проводника с токами А₁ и А₂. Опыт показывает, что, если они движутся совместно, то есть таким образом, что их относительное положение остается неизменным, то ни в том, ни в другом проводнике никаких индукционных явлений не наблюдается. Отсюда следует, что изменение магнитного потока Ф₁₂, исходящего от А₁ и проходящего через А₂ вызывает в А₂ один и тот же индукционный эффект независимо от того, обусловливается ли это изменение движением А₂ или движением А₁. Далее, однако, представляется естественным предположить, что индукционный эффект в неподвижном проводнике А₂, вызываемый изменением магнитного потока Ф₁₂, не зависит от специальных условий, которыми определяется это изменение, — например, от движения ли проводника А₁, или от изменения силы тока в нем. Мы приходим, таким образом, к явлению индукции совершенно иного типа, нежели то, из которого мы исходили, а именно — к возбуждению электродвижущей силы в неподвижном проводнике вследствие изменения силы тока в другом также неподвижном проводнике. Механизм электромоторной индукции этого типа совершенно иной, нежели у индукции первого типа, обусловленной движением рассматриваемого проводника в постоянном магнитном поле. Там дело сводилось к обычному электрокинетическому взаимодействию, то есть к созданию одним движущимся зарядом магнитного поля, действующего на другой так же движущийся заряд. Здесь, то есть в случае индукции нового типа, мы имеем дело с силой, действующей на неподвижные заряды, то есть с силой, обусловленной присутствием не магнитного, а электрического поля, создаваемого зарядами, образующими переменный электрический ток. Так как сила тока пропорциональна скорости зарядов, то быстрота изменения силы тока di/dt, которой определяется рассматриваемый эффект, должна быть прямо пропорциональна ускорению этих зарядов. Таким образом, оказывается, что ускоренное движение электрических зарядов возбуждает электрическое поле, пропорциональное ускорению. Этим не кулоновым, а так сказать «фарадеевым» электрическим полем (явления индукции были впервые открыты и изучены Фарадеем) и обусловливается рассматриваемый индукционный эффект. Можно показать, что к тому же самому механизму, то есть фарадееву электрическому полю, сводится индукционный эффект, обусловленный движением индуктирующего проводника при неизменности силы тока.

Строение фарадеевского поля будет подробно изучено нами в следующей главе. Здесь же мы ограничимся несколькими соображениями, вытекающими из предыдущего и относящимися к вопросу об энергии электрических токов.

Мы видели выше, что работа поперечных пондермоторных сил, действующих между двумя проводниками А₁ и А₂, может быть выведена из некоторой потенциальной энергии их: U₁₂ = -L₁₂i₁i₂. Так как сумма этой работы и работы продольных электромоторных сил, индуктируемых в каждом из проводников благодаря его движению в поле другого, равна нулю, то отсюда следует, что последняя работа может быть определена как уменьшение некоторой энергии Т₁₂ = -U₁₂ = L₁₂i₁i₂. Но движение каждого проводника, наряду с индукционной электродвижущей силой магнитного происхождения в нем самом, вызывает индукционную электродвижущую силу той же самой величины, но уже не магнитного (электрокинетического), а электрического (фарадического) происхождения в другом проводнике. Таким образом, полная энергия обоих проводников, то есть та величина, уменьшением которой определяется работа всех сил, действующих на находящиеся в них заряды, равна сумме 2Т₁₂ + U₁₂ = Т₁₂. В виду компенсации работы поперечных и продольных сил магнитного происхождения, можно считать, что энергия

целиком определяет работу одних лишь фарадических сил, то есть индукционных электродвижущих сил электрического происхождения. Ее можно определить как работу, которую нужно затратить против этих сил, чтобы при данном положении обоих проводников, определяемом коэффициентом взаимной индукции L₁₂, создать в них токи i₁ и і₂. Аналогичным образом в случае отдельного проводника энергия

представляет собой меру работы, которую нужно затратить для создания в нем тока i₁, или, вернее, для преодоления той электродвижущей силы самоиндукции, которая вызывается в нем изменением силы тока от нуля до данного значения. Эту электродвижущую силу самоиндукции можно рассматривать как результирующую электродвижущих сил взаимной индукции между бесконечно тонкими струями, на которые можно (мысленно) расчленить ток в данном проводнике. Обозначая ее через V₁₁ и замечая, что работа ее за единицу времени равна V₁₁ i₁с, имеем

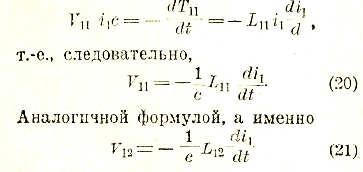
определяется электродвижущая сила, индуктируемая в проводнике А₂ вследствие изменения силы тока в (неподвижном) проводнике A₁. Здесь L₁₂i₁ представляет собой не что иное, как магнитный поток Ф₁₂. По аналогии величину L₁₁і₁ = Ф₁₁ можно определить как магнитный поток, исходящий от данного тока и проходящий через его собственный контур. Это определение лишено, однако, ясного физического смысла, поскольку при рассмотрении собственной энергии тока проводник, по которому он течет, нельзя рассматривать как бесконечно тонкую линию.

Энергия Т₁₁ = Т может быть выражена как сумма бесконечно малых элементов вида

составленных для всех зарядов, образующих данный ток [см. формулу(4)]¹). Разделяя проводники на бесконечно малые элементы объема dV и замечая, что электрическое количество движения, связанное с каждым из этих элементов, равно произведению его на плотность тока, мы получаем для энергии Т сумму выражений вида

для всевозможных элементов объема, взятых попарно (ϴ представляет собой угол между направлениями векторов, плотности тока в элементах dV' и dV'').

Подобно тому, как и соответствующее выражение для электростатической энергии некоторого объемного распределения электрических зарядов, предыдущее выражение может быть преобразовано в сумму выражений вида

взятых для всего пространства, где магнитное поле отлично от нуля. Таким образом энергию Т, которая, как мы видели выше, измеряет работу индукционных электрических сил, возбуждаемых изменением магнитного поля, можно трактовать как энергию, связанную с этим полем и распределенную в пустом пространстве с объемной плотностью Н²/8π.

¹) При этом каждая пара зарядов должна входить в сумму всего лишь один раз.

Это определение магнитной энергии вполне соответствует определению электрической энергии, как величины, связанной с электрическим полем и распределенной в пространстве с объемной плотностью Е²/8π. Далее, легко показать, что пондермоторные силы, действующие между проводниками с током, могут быть сведены, подобно электростатическим силам между наэлектризованными телами, к натяжению Н²/8π вдоль магнитных силовых линий и давлению Н²/8π в поперечном направлении.

Предыдущие результаты легко обобщаются на случай любой системы токов, причем под Т в этом случае следует понимать полную величину их магнитной энергии, то есть, например, в случае двух токов величину

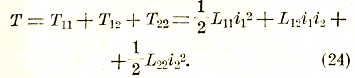
Заметим, что магнитная энергия, так, как мы ее определили в этом параграфе, представляет собой большое сходство с кинетической энергией системы материальных частиц. Это сходство выступает особенно отчетливо в случае отдельного проводника (соответствующем случаю отдельной частицы). Здесь сила тока играет роль скорости v, а коэффициент самоиндукции — роль массы m в обычном выражении для кинетической энергии 1/2 mv². То, что сходство это имеет не поверхностный характер, а лежит в существе дела, вытекает из того обстоятельства, что сила тока на самом деле пропорциональна скорости движения зарядов в проводнике. Далее, электродвижущая сила самоиндукции -Ldi/dt представляет собой полный аналог силы инерции -m dv/dt; ее можно трактовать как силу инерции электрического тока.

Аналогия между магнитной и кинетической энергией не выдерживается полностью в случае системы токов или системы частиц. Здесь наряду с суммой членов, соответствующих отдельным токам (или частицам), мы имеем члены, характеризующие взаимодействие разных токов. Им должны были бы соответствовать члены, пропорциональные произведению скоростей различных частиц, то есть члены вида m₁₂v₁v₂, которые можно было бы определить как взаимную кинетическую энергию этих частиц, причем коэффициенты m₁₂, аналогичные коэффициентам взаимной индукции, можно было бы трактовать как «взаимную массу». Точно так же сила инерции, испытываемая какой-нибудь частицей, должна была бы слагаться из обычной силы инерции или «самоинерции» и сил взаимной инерции и т. д., определяемых ускорениями остальных частиц.

Развитие электрической теории материи привело к преобразованию старых представлений о кинетической энергии и инерции в духе только что изложенных представлений. А именно, поскольку элементарные частицы материи обладают электрическими зарядами, движение их должно сопровождаться такими же электромагнитными эффектами, как и движение зарядов в проводниках. В частности, например, при ускоренном движении электрона (или протона) элементы его заряда должны оказывать друг на друга индукционное действие, обусловленное их фарадеевским полем и сводящееся к силе, пропорциональной ускорению и обратной ему по направлению. Эта сила самоиндукции электрона ничем, следовательно, не отличима от обыкновенной силы инерции. Представляется, поэтому, вполне естественным отождествить последнюю с первой, то есть, другими словами, рассматривать силу инерции электрона (или протона) как электродвижущую силу самоиндукции связанного с ним заряда. С этой точки зрения масса электрона оказывается электромагнитной величиной, обусловленной его зарядом, или, вернее, фарадеевским взаимодействием элементов этого заряда, причем сам электрон (или протон) оказывается не чем иным, как электрическим зарядом, сосредоточенным в некотором элементе объема. Последний должен иметь конечную величину, так как в противном случае масса электрона оказалась бы бесконечной. Обычно электроны и протоны представляются в виде шариков, заряд которых равномерно распределен по их объему или поверхности. Радиус этих шариков должен быть тем меньше, чем больше их масса. Вычисление последней проще всего можно произвести, исходя не из силы инерции (самоиндукции), которая появляется при ускоренном движении, а из кинетической, то есть магнитной энергии, которая определяется скоростью. Пользуясь формулой (6), нетрудно показать, что заряд е, распределенный внутри или на поверхности шара, создает вне шара такое же магнитное поле, как если бы он был сосредоточен в центре, то есть поле

где Е — кулоновское электрическое поле, создаваемое им в той же самой точке. Это соотношение между электрическим и магнитным полем равномерно движущегося заряда остается в силе и для внутренних точек. Отсюда следует, что магнитная энергия, то есть интеграл ∫ Н²/8π dv, взятый по всему пространству, равен электрической энергии кулонова поля ʃ Е⁸/8π dv, умноженной на среднее значение множителя v²/c² sin ϴ для различных значений угла ϴ между вектором скорости и радиус-вектором соответствующей точки пространства относительно центра заряда. В случае шаровой симметрии среднее значение sin² ϴ сводится к 2/3, и мы получаем таким образом следующее соотношение между магнитной энергией Т и электрической U:

В случае шарика радиуса а с поверхностным зарядом е, энергия U равна е/2а. Таким образом, предыдущее выражение для магнитной энергии может быть переписано в виде причем масса m оказывается равной

Подставляя сюда значения е = ± 4,77 · 10^-10 и с = 3 · 10¹⁰, мы получаем в случае электрона (m = 9 · 10^-28) а = 2 · 10^-13 см, а в случае протона, имеющего примерно в 2 000 раз большую массу, соответственно, то есть в 2 000 раз, меньший радиус.

Согласно обычным представлениям о массе, последняя является свойством аддитивным, то есть масса системы, образованной несколькими частицами, равняется сумме масс этих частиц, взятых в отдельности. С точки зрения вышеизложенной электромагнитной теории массы, подобная аддитивность не имеет места. В случае системы, образованной совокупностью нескольких электронов или протонов, например, атома или атомного ядра у сложных атомов, к сумме масс отдельных частиц необходимо прибавить их взаимные массы, характеризующие силы взаимной индукции, которые они оказывают друг на друга при ускоренном движении. Эти взаимные массы тем больше, чем ближе разные частицы друг к другу. При этом в случае одноименных частиц они имеют положительные, а в случае разноименных частиц — отрицательные значения. Если в рассматриваемой системе разноименные частицы ближе друг к другу, чем одноименные (так что притяжение преобладает над отталкиванием и система для своего расчленения требует некоторой энергии), то сумма всех взаимных масс оказывается отрицательной. Мы получаем в этом случае дефект массы. Подобный дефект массы имеется у всех материальных тел; однако, заметной величины он достигает лишь у ядер сложных атомов, в виду их чрезвычайно малых размеров, то есть чрезвычайно тесной упаковки электронов и протонов, их образующих. Дефект этот составляет около 0,8% массы каждого протона, то есть он в 16 раз больше массы электрона (по отношению к массе всех электронов, имеющихся в ядре, он еще больше, так как число этих электронов меньше числа протонов).

Этим объясняется то обстоятельство, что, принимая атомный вес кислорода за 16, или гелия за 4, для водорода получают атомный вес 1,008, между тем как атом кислорода состоит ровно из 16, а атом гелия из 4 атомов водорода.

§ 4. Магнетизм (ср. XXVII, 579' след.). Электрокинетические взаимодействия и связанные с ними индукционные явления были впервые обнаружены в замаскированной форме, а именно в форме сил взаимодействия между особыми телами, называемыми магнитами. Силы взаимодействия между постоянными магнитами были количественно изучены Кулоном, почти одновременно с силами взаимодействия между наэлектризованными телами. При этом Кулон пришел к выводу, что магнитные силы, подобно электрическим, обусловливаются наличием «магнитных полюсов», совершенно аналогичных по своим действиям друг на друга электрическим зарядам. В каждом магните, или теле, способном намагничиваться, магнитные полюса противоположного знака находятся в эквивалентных количествах, подобно электрическим зарядам противоположного знака в нейтральном теле. Однако, в отличие от электрических зарядов отделение магнитных полюсов противоположного знака друг от друга оказывается абсолютно невозможным. Таким образом, явления магнетизации, аналогичного электризации в обычном смысле слова, никогда не наблюдается. Магнит, или способное намагничиваться тело, ведет себя совершенно таким же образом, как поляризованный или могущий поляризоваться диэлектрик, причем явление намагничения оказывается аналогичным не электризации, а поляризации диэлектрика.

В начале XIX века Вебер ввел представление о том, что магнетизм является молекулярным свойством, то есть что молекулы магнита представляют собой маленькие магнитики, ориентированные одинаковым образом. В теле, способном намагничиваться, они при обычных условиях ориентированы беспорядочно, но под влиянием внешнего магнитного поля приобретают одинаковую ориентировку, которая и проявляется в намагничении. Связь магнитных явлений с электрическими была впервые установлена Эрстедтом, показавшим, что электрический ток оказывает ориентирующее действие на магнитную стрелку, то есть создает магнитное поле, по существу тождественное с полем обыкновенного магнита. Далее выяснилось, что и обратно магнит оказывает действие на проводник с электрическим током. Вслед за взаимодействием между электрическими токами и магнитами обнаружилось, что и электрические токи сами по себе оказывают друг на друга такое же действие, как и магниты. Основные законы взаимодействия электрических токов, которые были рассмотрены нами выше, были установлены французскими физиками Био, Саваром и в особенности Ампером. Именно последний показал, что замкнутый электрический ток по действиям, производимым им на другие токи (или магниты) или испытываемым со стороны последних, эквивалентен магниту. Эквивалентность магнитов и токов привела Ампера к мысли о полном упразднении магнетизма как самостоятельного явления, то есть о сведении его к взаимодействию электрических токов, циркулирующих в намагниченном веществе. Исходя из гипотезы Вебера о молекулярных магнитиках, Ампер предложил трактовать их как элементарные молекулярные токи, то есть токи, циркулирующие внутри молекул и отличающиеся от обычных токов только отсутствием сопротивления, то есть, следовательно, способностью оставаться неизменными неограниченно долгое время.

Наконец, в начале XX века, в связи с развитием электронной теории, выяснилось, что молекулярные токи Ампера образуются вращательным движением отдельных электронов в атомах. При этом вначале имелось в виду лишь обращение электронов вокруг центрального тела атома — положительного ядра. В последнее же время выяснилось, что, помимо этого обращения, электроны обладают вращением около собственной оси, также сообщающим им свойства магнитиков, и что именно от этого осевого, а не орбитного вращения электронов зависят свойства сильномагнитных веществ, каковыми являются железо и другие «ферромагнитные» тела, как, например, кобальт, никель и т. д.

Связь магнитных свойств с вращательным движением электронов была особенно отчетливым образом установлена опытом Эйнштейна и де Гааса, показавшим, что перемагничение железного стержня вызывает его вращение в ту или другую сторону, а также опытом Барнета, установившим, что вращение тела вокруг оси оказывает на него такое же намагничивающее влияние, как и внешнее магнитное поле, параллельное этой оси. Возможно, что в этом явлении кроется причина земного магнетизма, а также намагничения Солнца и, по-видимому, всех других небесных тел, обладающих осевым вращением. Таким образом, отдельные атомы с быстро обращающимися в них электронами или даже отдельные электроны, вращающиеся вокруг собственной оси, ведут себя в этом случае совершенно так же, как маленькие волчки или жироскопические компасы (при медленном вращении вокруг некоторой оси подобного волчка, быстро вращающегося вокруг собственной оси, последняя стремится повернуться в направлении первой оси). Следует, впрочем, заметить, что магнитное поле земного шара во много миллиардов раз сильнее того магнитного поля, которое по своему ориентирующему действию было бы эквивалентно вращению земли вокруг оси.

Как впервые показали опыты Вейсса, магнитный момент отдельных атомов, ионов или электронов, подобно электрическому заряду ионов, может принимать лишь значения, равные или кратные некоторой минимальной величине, представляющей собой как бы атом магнитного момента и называемой магнетоном. Это обстоятельство указывает на то, что размеры и наклонность орбит, описываемых электронами в атомах, не могут изменяться непрерывным образом, но образуют некоторую дискретную совокупность различных возможностей.

Не углубляясь в рассмотрение причин этой дискретности (относящихся к квантовой теории строения атомов, подробнее см. энергия), мы перейдем теперь к обзору важнейших магнитных свойств материальных тел. Последние с точки зрения этих свойств обычно делятся на 3 класса, а именно: на сильномагнитные, или ферромагнитные, на парамагнитные и диамагнитные. Первые могут сохранять магнитный момент и в отсутствии внешнего поля (остаточное намагничение), тогда как вторые и третьи могут намагничиваться лишь в присутствии внешнего магнитного поля (источником которого служит обычно электрический ток). При этом парамагнитные тела намагничиваются в направлении магнитного поля, тогда как диамагнитные — в диаметрально противоположном направлении. Это различие проявляется внешне в том, что парамагнитные тела втягиваются магнитным полем (то есть притягиваются к его источникам), тогда как диамагнитные — выталкиваются им.

Сущность различия между пара- и диамагнитными телами лежит, как показал Ланжевен, в совершенно различном механизме намагничения в обоих случаях. В случае парамагнитных веществ механизм этот сводится к ориентировке частиц, обладающих постоянным отличным от нуля магнитным моментом и способных вращаться независимо друг от друга (ими могут быть молекулы, атомы или отдельные электроны). Ориентирующему влиянию внешнего магнитного поля противодействует влияние теплового движения, стремящегося разбросать магнитные оси этих частиц совершенно беспорядочным образом. Результирующая степень ориентации, определяемая величиной намагничения, то есть магнитным моментом единицы объема, зависит в этом случае от отношения напряженности магнитного поля Н к абсолютной температуре Т и при не слишком больших значениях отношения Н/Т оказывается прямо пропорциональной ему (закон Кюри-Ланжевена).

В случае диамагнитных тел, как показал тот же Ланжевен, мы имеем дело не с ориентацией готовых магнитиков, а с явлением электромагнитной индукции, в отдельных атомах или молекулах. Представим себе последние, следуя Амперу, в виде очень маленьких идеальных проводников (то есть проводников, не обладающих вовсе сопротивлением) и предположим, что при нормальных условиях никакого тока в них нет. При внесении подобных частиц в магнитное поле или при создании последнего, появляются рассмотренные нами выше индукционные электродвижущие силы, которыми создаются молекулярные токи, сообщающие частицам свойства магнитиков. При этом оси последних оказываются направленными в сторону противоположную той, в которую поле стремилось бы их ориентировать (принцип Ленца). Заменяя представление об идеальном молекулярном проводнике представлением об атоме, образованном вращением электронов вокруг положительного ядра, мы получаем вместо индукционных амперовых токов некоторое изменение в скорости обращения электронов по их орбитам, вызывающее такой же добавочный магнитный момент, как и эти токи. Если при нормальных условиях результирующий магнитный момент атома равняется нулю (благодаря компенсации магнитного действия разных электронов) или если эти моменты, несмотря на присутствие поля, остаются беспорядочно ориентированными (что, например, может иметь место при высокой температуре), то в результате действия магнитного поля тело, образованное рассматриваемыми атомами, намагничивается в направлении, противоположном полю. В общем случае наличия начального момента у атомов и ориентации их полем, диамагнитный эффект налагается на парамагнитный, обычно ослабляя, а иногда и совершенно маскируя его.

Парамагнитный эффект представляет собой полный аналог ориентационной поляризации диэлектриков, а диамагнитный аналогичен деформационной поляризации последних (ср. гл. I, § 7). При этом статической деформации, выражающейся в смещении электронных орбит под действием электрических сил, соответствует в магнитном случае так называемое прецессионное вращение этих орбит вокруг магнитного поля, то есть медленное вращение неискаженных орбит вокруг прямой, проходящей через центр атома в направлении поля. Следует заметить, что действие магнитного поля, после установления его, сводится лишь к поддержанию этой («ларморовской») прецессии, тогда как создается она теми электрическими силами, которыми сопровождается создание магнитного поля или введение тела в него.

В случае ферромагнитных тел, так же как и в случае парамагнитных, намагничение сводится к чисто ориентационному эффекту. Различие между ними сводится к тому, что в первом случае основным фактором, обусловливающим эту ориентацию, является не внешнее магнитное поле, как во втором, но особого рода внутреннее или молекулярное поле (по терминологии Вейсса). Последнее имеет чисто электрическое происхождение и лишь проявляется в стремлении одинаково сориентировать соседние элементарные магнитики, которыми, как показали новейшие исследования, являются в случае ферромагнитных металлов отдельные свободные электроны.

У кристаллов кубической системы, к которым принадлежат ферромагнитные металлы, это направление остается совершенно неопределенным. При наличии же незначительных местных искажений кристаллической решетки оно определяется в каждом месте характером этой деформации или соответствующими внутренними упругими напряжениями. Поскольку последние распределены в теле неправильным образом, результирующее намагничение в среднем для каждого небольшого объема тела исчезает. Таким образом, тело в целом, несмотря, на наличие в нем «спонтанного» намагничения, представляется не намагниченным (Вейсс).

При отсутствии этих внутренних напряжений сколь угодно слабое внешнее поле сразу же повернуло бы все магнитики в своем собственном направлении, так как будучи уже ориентированы по отношению друг к другу они без всякого сопротивления, повернулись бы в указанном им направлении, — подобно тому, как взвод солдат поворачивается по приказанию командира.

При наличии же внутренних напряжений, поворот магнитиков в отдельных однородных областях может осуществляться лишь постепенно, путем борьбы внешнего магнитного поля с ориентирующим влиянием местного искажения решетки (например, растяжения или сжатия ее в том или ином направлении). Исследование этого вопроса (Беккер) показывает, что зависимость результирующего намагничения от внешнего поля не является однозначной функцией последнего, но оказывается различной при возрастании и при последующем убывании поля (с переменой направления его на противоположное).

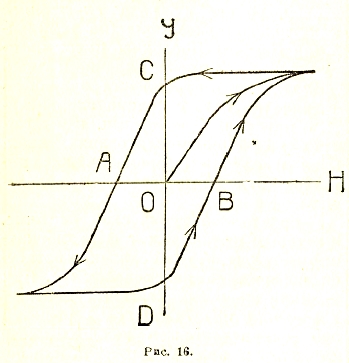
Рис. 16.

Это явление, представляющее собой одну из характерных особенностей ферромагнитных тел, называется гистерезисом. Кривая гистерезиса изображена на рис. 16. На горизонтальной оси отложены значения поля (магнитной напряженности), а на вертикальной — намагничения (магнитного момента единицы объема). Отрезок ОС представляет собой величину остаточного намагничения при постепенном убывании поля до нуля в одном направлении (влево), а отрезок OD — то же самое для другого направления. Отрезки ОА и ОВ определяют так называемую «коэрцитивную силу», то есть то внешнее магнитное поле, которое необходимо для ликвидации остаточного намагничения. Опыт показывает, в согласии с набросанной выше теорией, что ширина гистерезисной петли тем больше, чем больше внутренние напряжения в соответствующем теле.

При более тщательном исследовании оказывается, что с изменением поля Н намагничение изменяется не плавным образом, как это изображено на кривой, но скачкообразно, причем величина скачков (соответствующих мгновенному перемагничению маленького объема тела) особенно велика на крутых участках гистерезисной петли. Это явление носит название эффекта Баркгаузена.

Ферромагнитные тела имеют большое значение в электротехнике по той причине, что они позволяют в чрезвычайно высокой степени усиливать магнитные поля, создаваемые слабыми или не очень сильными электрическими токами, а вместе с тем и различные пондермоторные и индукционные эффекты, связанные с этими полями. Это усиление сводится к тому, что к внешнему полю, ориентирующему элементарные магнитики, присоединяется то магнитное поле, которое ими самими создается и которое может превышать первое во много тысяч раз. В случае пара- и диамагнитных тел вторичное поле составляет обычно лишь ничтожную долю (порядка одной стотысячной) первичного. Следует заметить, что ферромагнитные свойства сохраняются у железа и других металлов этого типа лишь в твердом состоянии и то лишь до определенной «критической» температуры — так называемой температуры Кюри, — выше которой они ведут себя как обыкновенные парамагнитные тела. Роль температуры или, вернее, теплового движения сводится в этом случае к противодействию ориентирующему влиянию внутреннего или молекулярного поля. При температуре Кюри это ориентирующее влияние исчезает, и тело из ферромагнитного состояния переходит в парамагнитное.

Мы уже указывали выше на аналогию намагничения с поляризацией диэлектриков. Вектору поляризации (то есть электрическому моменту единицы объема) во втором случае соответствует вектор намагничения в первом. При этом поверхностной плотности связанного электрического заряда, определяемой нормальной проекцией вектора, соответствует поверхностная плотность связанного электрического тока, определяемая тангенциальной (то есть параллельной поверхности) проекцией вектора.

Заменяя амперовы молекулярные токи молекулярными магнитиками и поверхностную плотность тока поверхностной магнитной плотностью, можно построить математическую теорию намагничения по тому же шаблону, который уже был установлен нами в случае электрической поляризации. Таким образом, вводится понятие о (средней) магнитной напряженности внутри намагниченного тела и магнитной индукции, далее — о магнитной восприимчивости тела χ = I/H и магнитной проницаемости μ = B/H, играющей роль диэлектрической постоянной. При этом для векторов  и  устанавливаются те же самые граничные условия, то есть непрерывность тангенциальной проекции первого и нормальной проекции второго, как и для векторов в случае поляризации диэлектриков.

Однако, если с точки зрения фиктивных молекулярных магнитиков перейти на точку зрения реальных молекулярных токов, то оказывается, что вектор, называемый магнитной индукцией, на самом деле представляет собой среднее магнитное поле в теле, соответствуя в этом смысле не вектору, но вектору в случае диэлектриков; вектор же представляет собой вспомогательную величину, соответствующую вектору электрической индукции но с обратным знаком при векторе поляризации.

Кусок железа или какого-либо другого ферромагнитного вещества, намагничивающийся под влиянием электрического тока, называется электромагнитом. Для намагничения железного стержня его обычно вводят внутрь катушки, на которую намотана в определенном направлении изолированная проволока, и пропускают через последнюю электрический ток. Подобная катушка называется соленоидом. Если длина ее велика в сравнении с толщиной, то внутри нее получается практически однородное магнитное поле с напряженностью

где i — сила тока, а w — число витков проволоки, приходящихся на единицу длины катушки. При наличии в катушке сердечника с магнитной проницаемостью μ поле внутри катушки увеличивается в μ раз. При этом, однако, говорят, что изменилось не поле, а вектор индукции, при отсутствии сердечника равнявшийся, а при наличии его принимающий значение

Коэффициент самоиндукции подобной катушки может быть вычислен приближенно на основании следующих соображений. Каждый виток катушки пронизывается магнитным потоком μНS, исходящим преимущественно от других витков, где S площадь поперечного сечения катушки. Обозначая длину ее через l, мы видим, что через все витки проходит магнитный поток

Ф = μHS lw = 4πμ w² Sli.

Отсюда следует, что коэффициент самоиндукции рассматриваемой катушки равен

L = 4πμw²V, (28)

где V = Sl объем ее, или, вернее — внутреннего пространства, где сосредоточено поле Н. Заметим, что вне катушки последнее практически исчезает.

Подставляя это выражение в формулу Т = 1/2Li² для магнитной энергии тока и заменяя в ней wi через H/2π согласно (27), получаем

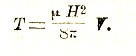
Таким образом, мы можем себе представить, что энергия тока сосредоточена в сердечнике катушки и распределена в ней с объемной плотностью

Это выражение совершенно аналогично с уже известным нам выражением εЕ²/8π для объемной плотности электрической энергии в диэлектрике с диэлектрической постоянной ε. Если на рассмотренную выше катушку намотать проволоку, изолированную от первой, то мы получим прибор, который в зависимости от характера тока, пропускаемого через первичную обмотку, является индукционной катушкой (Рюмкорфа) или электрическим трансформатором (см. спираль Рюмкорфа). В первом случае через первичную обмотку пропускается ток постоянного направления, прерываемый через определенные промежутки времени (путем разрыва цепи, по которой он течет). При включении этого тока во вторичной обмотке индуктируется ток обратного направления; наоборот, при выключении его — ток того же самого направления. Эти индукционные токи тем сильнее — но вместе с тем и кратковременнее, — чем быстрее происходит изменение первичного тока. Обычно спадание его при выключении происходит гораздо быстрее, нежели нарастание при включении. Поэтому во вторичной обмотке индуктируется гораздо более сильный ток при выключении первичного тока, нежели при его включении. Индукционная электродвижущая сила тем больше, чем больше число витков во вторичной обмотке. Обычно последнее берется чрезвычайно большим, — так, чтобы разность потенциалов, появляющаяся на концах вторичной цепи (в разомкнутом состоянии) при размыкании первичного тока была бы достаточна для проскакивания искры желаемой длины (см. рис. 17). Заметим, что при размыкании первичного тока между концами его цепи также проскакивает искра, вызываемая электродвижущей силой самоиндукции, которая возбуждается в нем вследствие быстрого убывания силы тока. При замыкании тока, искры, разумеется, не происходит. В этом случае, при наличии постоянной первичной электродвижущей силы V, сила тока возрастает сравнительно медленно, постепенно приближаясь к предельной величине і = V/R соответствующей данному сопротивлению цепи R. Скорость этого возрастания определяется отношением сопротивления к коэффициенту самоиндукции цепи L. В случае обычных цепей она настолько мала, что нормальный ток і устанавливается в незначительную долю секунды.

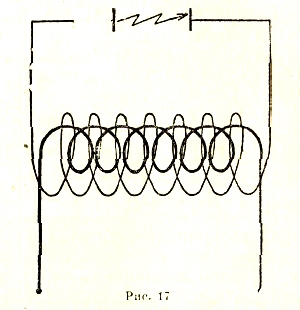
Рис. 17.

Заметим, что разность между этим током и тем током і (t), который фактически течет в цепи при замыкании ее, называется экстратоком замыкания. Аналогичным образом ток, текущий в цепи после ее размыкания (и прорывающийся через воздух в виде искры), называется экстратоком размыкания. Само собой разумеется, что подобные экстратоки наблюдаются не только в цепи катушки, но и во всякой другой цепи.

Наряду с постоянными токами в электротехнике имеют чрезвычайно широкое применение так называемые переменные токи. Под этим названием подразумевается обычно не всякий ток переменной силы или направления, но ток, сила и направление которого колеблется маятникообразно или гармонически по формуле

где i₀ представляет собой амплитуду тока, Т — период колебаний, а α — так называемую начальную фазу. Заметим, что величина обратная периоду f  = 1/Т, то есть равная числу колебаний, или «циклов» в единицу времени, называется частотой, а пропорциональная ей величина ω = 2πf — угловой частотой. Таким образом «переменный ток» представляет собой по существу электрические колебания синусоидального характера, или, точнее, гармоническое колебательное движение электрических зарядов в проводнике.

Источником переменного тока служит обычно динамо-машина, схема которой была уже рассмотрена нами в § 3. Мы видели, что при вращении рамки (якоря) в однородном магнитном поле, в нем индуктируется электродвижущая сила, равная V = 1/c SHωsinϕ, или, если  положить здесь

Таким образом, эта электродвижущая сила в смысле своей зависимости от времени имеет такой же колебательный характер, как и переменный электрический ток, определяемый формулой (30). Естественно, что именно такой ток ею и вызывается. Если бы проводник, в котором возбуждается электродвижущая сила (31), не имел бы вовсе омического сопротивления, то сила вызываемого ею тока должна была бы определяться из условия равенства и противоположности силы электродвижущей самоиндукции, связанной с этим током и равной -1/сLdi/dt. Равенство 1/сLdi/dt = V на самом деле выполняется, если положить в формуле (30) α = π/2, то есть i = i₀ cos ωt и

Таким образом, в рассматриваемом идеальном случае (проводника без сопротивления) мы получаем переменный электрический ток, сдвинутый по фазе относительно электродвижущей силы на четверть периода, причем роль омического сопротивления, определяемого отношением электродвижущей силы к силе тока, играет величина ω/сL, называемая индуктивным сопротивлением.

В общем случае при наличии у проводника омического сопротивления R оно складывается с индуктивным сопротивлением, но не арифметически, а «геометрически», то есть так, как складываются друг с другом два катета прямоугольного треугольника в его гипотенузу. Таким образом, полное¹) сопротивление R', определяемое как отношение амплитуды электродвижущей силы V₀ к амплитуде вызываемого ей тока i₀, выражается в этом случае формулой

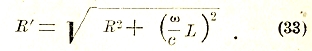
При этом угол сдвига фазы тока по отношению к электродвижущей силе, то есть величина α в формуле (30), оказывается меньшей π/2. Можно показать, что он равен одному из двух острых углов в прямоугольном треугольнике с катетами R  и ω/сL, а именно тому из этих углов, который обращается в нуль при L = 0 и, следовательно, в прямой угол при R = 0.

Предыдущие соотношения значительно усложняются, когда рассматриваемый проводник, в котором действует электродвижущая сила V, находится в индуктивной связи с каким-нибудь другим замкнутым проводником. «Индуктивная связь» двух проводников или контуров означает наличие взаимной индукции между ними и измеряется отношением коэффициента взаимной индукции их L₁₂ к среднему геометрическому из коэффициентов самоиндукции (величина

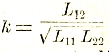
называется коэффициентом связи). Максимальная связь (с коэффициентом близким к 1) осуществляется в рассмотренной выше схеме катушки с двумя обмотками, намотанными одна на другую.

¹) В технике, обычно, омическое, индуктивное и полное сопротивления соответственно называются: активным, реактивным и кажущимся.

Впрочем, при наличии замкнутого (кольцеобразного) железного сердечника, магнитные силовые линии проходят практически полностью внутри последнего, так что в этом случае индуктивная связь между обеими обмотками не уменьшается, если они наматываются вокруг различных участков сердечника (рис. 18). При таких условиях результирующие электродвижущие силы V₁ и V₂, индуктированные в обеих обмотках и складывающиеся из силы самоиндукции и взаимной индукции (V₁ = V₁₁ + V₁₂, V₂ = V₂₂ + V₂₁), могут быть непосредственно вычислены, исходя из величины Ф полного магнитного потока, проходящего через любое поперечное сечение сердечника по формулам

где w₁ и w₂ обозначают числа витков в соответствующих обмотках. Отсюда следует, что эти индукционные электродвижущие силы относятся друг к другу, как числа витков w₁ и w₂.

Если в одной из обмоток — «первичной» — действует синусоидальная электродвижущая сила V типа (31), исходящая из какого-либо внешнего источника (например, динамо-машины), то электродвижущая сила того же типа — но с другой амплитудой — индуктируется во вторичной обмотке. Эта электродвижущая сила V₂ называется преобразованной, или «трансформированной» по отношению к исходной V, а самый прибор (схематически изображенный на рис. 18) называется электрическим трансформатором. Если первичная обмотка состоит из небольшого числа оборотов толстой проволоки с маленьким сопротивлением, то внешняя электродвижущая сила V, действующая в ней, практически уравновешивается той, которая в ней индуктируется V₁. Таким образом, отношение V₂/V₁, характеризующее трансформатор, практически совпадает с отношением V₂/V₁ = w₂/w_1. Если, следовательно, w₂ очень велико в сравнении с w₁, то преобразованная электродвижущая сила V₂ во вторичной обмотке оказывается очень большой по сравнению с первичной. В этом случае трансформатор может преобразовывать низкое напряжение V в высокое V₂. При обратном соотношении числа витков мы получаем обратное соотношение: трансформатор не повышает, а, наоборот, понижает напряжение, приложенное к первичной обмотке.

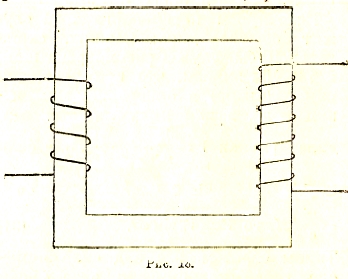
Рис. 18.

Мы не можем останавливаться здесь на вопросе о различных технических применениях переменных электрических токов. Одним из наиболее широко известных, но отнюдь не специфическим, является применение их к электрическому освещению (городские электрические станции дают обычно переменный ток с частотой 50). В связи с этим необходимо отметить, что тепловой эффект переменного тока, то есть, другими словами, количество тепла, выделяющегося при его прохождении за единицу времени, выражается не произведением силы тока і на электродвижущую силу V, как в случае постоянного тока, а формулой

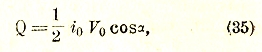
то есть половиной произведения амплитуд тока и электродвижущей силы на косинус угла, характеризующего сдвиг фазы между ними. В технике переменных токов величины

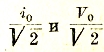
называются «эффективными» значениями силы тока и электродвижущей силы, причем произведение

характеризующее ту часть тока, с которой связан тепловой эффект, называется активной, а произведение

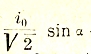
— реактивной слагающей тока. Эти обозначения соответствуют представлению обеих слагающих тока, как катетов прямоугольного треугольника, соответственно параллельного (то есть совпадающего по фазе) и перпендикулярного (то есть сдвинутого по фазе на 90°) к внешней электродвижущей силе. Переменные токи применяются, наряду с постоянными, для превращения электрической энергии не только в тепловую, но и в механическую, то есть в различного рода электродвигателях (моторах), в рассмотрение которых мы не можем здесь вдаваться (подробнее см. электротехника).

Заметим, что переменные токи могут быть легко преобразованы в постоянные или, вернее, в токи постоянного направления (но колеблющейся величины) при помощи приборов, называемых умформерами, или преобразователями. Заметим также, что динамо-машины переменного тока называются часто альтернаторами.

В заключение мы перечислим вкратце различные измерительные приборы, применяемые в электромагнетизме. Важнейшими из них являются приборы, служащие для измерения силы тока по производимому им магнитному (электрокинетическому) действию. В случае слабых токов эти приборы называются гальванометрами, а в случае сильных — амперметрами. Сила тока определяется в них по механическому действию, производимому одной частью цепи (неподвижной) на другую (подвижную) или же на постоянный магнит. Гальванометры и амперметры могут быть легко приспособлены к измерению разностей потенциала (электродвижущих сил), причем в этом случае они называются вольтметрами. В технике переменных токов широкое применение имеют приборы, служащие для измерения мощности (обычно — по тепловому эффекту) — так называемые ваттметры, а также электрической энергии, потребляемой за данное время (электрические счетчики).

Заметим, наконец, что в учении об электромагнитных явлениях часто пользуются особой, так называемой электромагнитной системой единиц, основывающейся на электромагнитной единице электрического тока или заряда, которая была введена нами в начале этой главы и которая в с = 3 · 10¹⁰ раз больше соответствующей электростатической единицы. Таким образом, электродвижущая единица заряда равна 10 кулонам, а электромагнитной силы тока — 10 амперам. Сохраняя в качестве единицы работы (энергии) 1 эрг, мы для электромагнитной единицы потенциала получаем величину в 3 · 10¹⁰ раз меньшую электростатической, то есть равную одной стомиллионной вольта. Практической единицей напряженности магнитного поля служит 1 гаусс, равный одной десятой соответствующей электромагнитной единицы. Наконец, практической единицей самоиндукции и взаимной индукции является так называемый генри = 10⁹ см. Напомним, что в электромагнитной системе единиц коэффициент самоиндукции (или взаимной индукции) измеряется в сантиметрах, так же как емкость — в электростатической системе единиц (см. электротехника — электрические измерительные приборы).