Электричество. Глава IV. Электромагнитные волны и электромагнитная теория света

Электричество. Глава IV. Электромагнитные волны и электромагнитная теория света. § 1. Ток смещения и распространение электромагнитных действий со скоростью света. Явление электромагнитной индукции в неподвижном проводнике связано с наличием этого проводника лишь в смысле своего обнаружения, а не происхождения. Мы можем и должны себе представить, что то электрическое поле, которое проявляется в виде индукционной электродвижущей силы в проводнике, сохраняется и при отсутствии его, являясь непосредственным следствием тех процессов, которыми обусловливается электромагнитная индукция в рассматриваемом случае. Процессы эти, как мы видели выше, сводятся, в конечном счете, к ускоренному движению электрических зарядов; индукционное электрическое поле — или, как мы его назвали, фарадеевское поле — обусловливается ускорением этого движения в таком же самом смысле, в каком магнитное поле обусловливается его скоростью. Поскольку, однако, в общую формулировку закона индукции, то есть в уравнение

в качестве фактора, определяющего фарадеевское поле, входит не движение электрических зарядов, а лишь, обусловливаемое ими магнитное поле, мы можем совершенно отвлечься от этого движения, представляющего собой основную причину явления, и рассматривать фарадеевское электрическое поле как непосредственное следствие изменения магнитного поля во времени, согласно уравнению (1). Но если переменное магнитное поле может в этом смысле являться непосредственным источником электрического, то, естественно, возникает вопрос — не может ли переменное электрическое поле являться непосредственным источником магнитного поля, аналогичного фарадеевскому? Этот вопрос был поставлен Максуэлом в 70-ых годах прошлого века и решен им в утвердительном смысле на основании следующих соображений.

Представим себе плоский конденсатор А, пластинки которого, после предварительного заряжения его, соединяются друг с другом с наружной стороны металлической проволокой В (рис. 19).

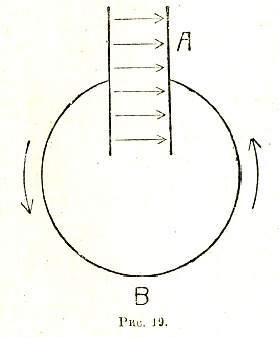
Рис. 19.

При этом конденсатор должен разрядиться; другими словами, по проволоке потечет электрический ток в направлении от положительной пластинки к отрицательной, что сопровождается уменьшением заряда его обкладок, а, следовательно, в электрического поля, действующего между последними. Это изменение электрического поля внутри конденсатора как бы заменяет собой или, вернее, дополняет электрический ток, текущий в проводнике, превращая его из незамкнутого «как бы» в замкнутый. Исходя из представления (по существу неправильного) о том, что всякий ток должен быть непременно замкнутым, Максуэл предложил трактовать переменное электрическое поле как особого рода ток, который он в отличие от обыкновенного «тока проводимости» (кондукционного) назвал током смещения. При этом физический смысл идеи Максуэла заключался в тождественности магнитных действий тока того и другого рода, то есть, иными словами, в предположении, что переменное электрическое поле создает магнитное поле того же типа, как и обыкновенный электрический ток.

Эти представления могут быть легко уточнены. Обозначая заряд положительной пластинки конденсатора через е, а площадь ее (равную, конечно, площади отрицательной) через S, мы имеем для напряженности электрического поля внутри конденсатора уже известную нам формулу

Таким образом,

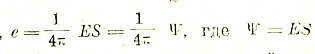
представляет собой электрический поток, проходящий через какое-либо сечение конденсатора. Принимая во внимание, что сила тока в электромагнитных единицах равна мы получаем соотношение

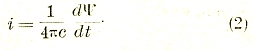
Эта формула показывает, что роль силы тока играет быстрота изменения электрического потока между обоими концами разомкнутого проводника, деленная на 4πс. Аналогичным образом плотности тока, то есть силе тока, отнесенной к единице поперечного сечения, соответствует величина

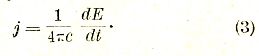
Обыкновенный замкнутый электрический ток окружен, как мы знаем, магнитным полем, силовые линии которого представляют собой замкнутые кольца, охватывающие контур тока. Если вычислить это поле согласно закону Био-Савара и составить для какого-нибудь контура, охватывающего контур тока, величину, соответствующую электродвижущей силе V в случае фарадеевского электрического поля, то оказывается, что эта величина V', называемая по аналогии «магнитодвижущей силой», связана с силой тока чрезвычайно простым соотношением

Заметим, что «магнитодвижущая сила» V' для какого-нибудь контура может быть определена как сумма произведений элементов этого контура dS на параллельную им слагающую магнитной напряженности (при определенном направлении обхода контура). В случае незамкнутого контура ее можно было бы определить как разность магнитных потенциалов на его концах. Формулу (4) нетрудно проверить на частном примере, а именно, если рассматриваемый контур совместить с одной из магнитных силовых линий в непосредственной близости к проводнику с током. Эти линии, как мы знаем, имеют форму кругов, причем на расстоянии r от оси проводника, то есть для круга радиуса r, магнитная напряженность Н равна 2i/r. Мы получаем, таким образом, в согласии с формулой (4).

Заменяя в этой формуле силу тока i ее выражением (2), мы приходим к формуле

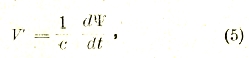
совершенно аналогичной формуле (1), выражающей  закон электромагнитной индукции. Нетрудно проверить, что они на самом деле отличаются только знаком. Это различие, как мы увидим дальше, имеет весьма существенное значение. Итак, мы видим, что убывающее электрическое поле создает вокруг себя магнитное поле, по своей структуре тождественное с электрическим полем, создаваемым возрастающим магнитным полем (и наоборот).

Закон, выражаемый формулой (5), можно было бы назвать законом «магнито-электрической индукции»¹), считая магнитодвижущую силу V' «индуцированной» изменением электрического потока через соответствующий контур.

Следует заметить, что формулы (4) и (5) представляют собой два предельных частных случая, первый из которых соответствует присутствию одного лишь тока проводимости (т. е. потока электрических зарядов), а второй — одного лишь тока смещения (т. е. переменного электрического потока). В общем случае наличия того и другого формула заменяется следующей:

Следует заметить так же, что здесь i и Ψ представляют собой потоки через тот контур, для которого определяется магнитодвижущая сила V'. Таким образом, если последний не охватывает контура тока i, а также в общем случае при отсутствии движущихся зарядов в рассматриваемой области пространства, формула (6) сводится к (5).

Ограничиваясь этим случаем, мы получаем следующую картину своеобразного сцепления между электрическим и магнитным полем. Изменение во времени одного из них вызывает появление другого. При этом магнитные силовые линии, образующиеся вокруг возрастающего электрического поля, охватывают его в виде колец в том же направлении, как и в случае обыкновенного тока (рис. 20а), а электрические силовые линии, образующиеся вокруг возрастающего магнитного поля, охватывают его также кольцеобразно, но в противоположном направлении. Исчезновение электрического поля сопровождается появлением магнитного, исчезновение магнитного — появлением электрического. Результатом этого взаимного порождения обоих полей является — как показал Максуэл (см. ниже) — перемещение их в пространстве со скоростью с.

¹) В настоящее время и советской литературе этот закон, в большинстве случаев, называется законом полного тока.

Это перемещение, или «распространение» электромагнитного поля из некоторой области, где оно было сосредоточено в начальный момент времени, происходит по тому же самому закону, которым определяется распространение какой-либо деформации (сжатия, растяжения и т. д.) в упругой однородной среде, например, в воздухе. Как известно, в последнем случае всякое нарушение равновесия распространяется обычно в виде звуковых колебаний, или волн. Аналогичные колебания и волны — но не механического, а электромагнитного характера — могут распространяться в пустом пространстве из какого-либо очага, где имеются источники переменного (во времени) электрического и магнитного поля, то есть колеблющиеся электрические заряды. Скорость с = 3 · 10¹⁰ см/сек., с которой распространяются в окружающем пространстве электрические и магнитные силы (или, вернее, напряженности) и которая может быть определена из опыта как отношение электромагнитной единицы электрического заряда к электростатической, в точности совпадает с непосредственно измеренной скоростью распространения света в пустоте. Смысл этого совпадения, которое уже было отмечено нами выше, заключается, очевидно, в том, что свет представляет собой электромагнитное явление, то есть, другими словами, что световые колебания и волны представляют собой не что иное, как волнообразно распространяющиеся колебания электрических и магнитных полей, и что источниками света, вызывающими эти «силовые» колебания, являются колеблющиеся электрические заряды (ср. свет, XXXVІІ, 563).

Мысль об электромагнитной природе света была высказана Фарадеем, который пришел к ней весьма простым, но по существу совершенно неправильным путем. А именно, в своих исследованиях об электрических и магнитных явлениях Фарадей руководствовался представлением о том, что электрические и магнитные силы передаются от одного тела к другому не непосредственно через разделяющую их пустоту (подобное «действие на расстоянии» казалось ему немыслимым), но через некоторую промежуточную материальную среду, заполняющую пространство, которое нам кажется совершенно пустым (ср. I главу, конец § 6).

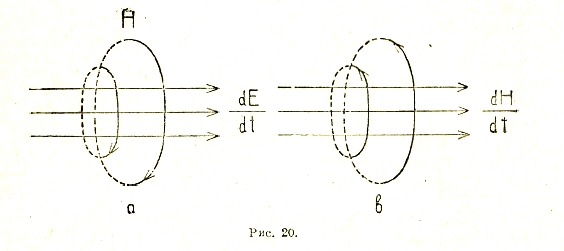
Рис. 20.

Подобная среда была введена еще за полтора века до Фарадея Гёйгенсом в качестве передатчика световых действий и утвердилась в физике под названием светового (или мирового) эфира (ср. физика, XLIII, 312 сл.). Представлялось естественным не создавать новой специальной среды для передачи электромагнитных действий и возложить соответствующие обязанности на тот же самый эфир. Таким образом, гипотеза эфира послужила соединительным звеном между областями физических явлений, дотоле казавшихся совершенно различными — электромагнетизмом и оптикой. Из представления о том, что электромагнитные и световые действия передаются через один и тот же эфир, непосредственно вытекало, во-первых, что электромагнитные действия должны распространяться со скоростью света и, во-вторых, что световые колебания можно рассматривать как колебания электрических и магнитных сил. При дальнейшем углублении и математическом развитии идей Фарадея Максуэл руководствовался той же самой гипотезой эфира как средоточия электромагнитных явлений, рассматривая электрические заряды и токи лишь как источники или очаги упругих напряжений и движений этой среды. Однако, логика вещей и опытные факты привели его к системе уравнений [по существу тождественных с приведенными выше уравнениями (1) и (6)], которые не могли быть согласованы ни с какими конкретными представлениями о механических свойствах эфира.

Некоторое время казалось, что сведение электромагнитных явлений к явлениям механическим, то есть к движению и взаимодействию материальных частиц, принципиально невозможно и что теория Максуэла приводит к необходимости замены старого механического мировоззрения новым электромагнитным, в котором основной реальностью является электромагнитное поле, существующее в пустом пространстве. Вскоре, однако, в связи с развитием электронной теории, выяснилось, что это поле существует не само по себе, но обусловливается элементарными заряженными частицами материи - электронами (и протонами), и что, следовательно, его можно рассматривать как простого посредника в действиях, оказываемых различными частицами друг на друга.

Таким образом, отвергнув гипотезу эфира, приведшую к представлению о конечной скорости распространения электромагнитных сил в пустом пространстве, и низведя электромагнитное поле на роль посредника между заряженными материальными частицами, физика восстановила поколебавшееся было механическое мировоззрение, но не в прежней форме, где действие между частицами на расстоянии считалось мгновенным, а в новой форме, где это действие, поскольку, по крайней мере, оно определяется электрическим зарядом частиц, является запаздывающим.

Сведение всех физических действий к электрическим (электромагнитным) и установление того принципа, что они передаются через пустоту не мгновенно, а с конечной скоростью, и составляет основное отличие нового механического мировоззрения от старого¹).

¹) Окончательное упразднение теории эфира связано с развитием теории относительности (см.), углубившей вместе с тем принципы новой «электромеханики».

§ 2. Основы теории электромагнитного излучения. Весьма распространенное представление об электромагнитных волнах, как о чем-то, существующем самостоятельно, совершенно не связанном с электрическими зарядами, в корне неправильно. Электромагнитные волны, как и всякое электромагнитное поле, обусловливаются электрическими зарядами. Покоящиеся заряды создают одно лишь кулоновское поле. Заряды, движущиеся прямолинейно и равномерно, создают, кроме того, магнитное поле Био-Савара. Наконец, заряды, движущиеся с некоторым ускорением, создают пропорциональное последнему электрическое поле, которое мы назвали «фарадеевским», и непосредственно с ним связанное, также пропорциональное ускорению, магнитное поле, которое мы назовем максуэловским. Конечная скорость распространения электромагнитных действий выражается при этом в том обстоятельстве, что электрическая и магнитная напряженность в каждой точке пространства определяется положением, скоростью и ускорением данного заряда не в тот момент времени t, для которого эти напряженности определяются, а в некоторый предшествующий момент времени t’, когда расстояние заряда от рассматриваемой точки R (t’) равнялось с (t—t’).

Это обстоятельство, которое обозначается как «запаздывание» электромагнитных действий, проявляется, конечно, лишь в том случае, когда заряд движется. В частности, при периодическом колебательном движении заряда, создаваемое им поле колеблется в каждой точке пространства с тем же самым периодом, но вообще говоря, не синхронно, а с некоторой разностью фаз, тем большей, чем больше расстояние этой точки от заряда или, вернее, среднего его положения. Таким образом, рассматривая электромагнитное поле в ряде точек, расположенных на различных расстояниях от последнего, мы получим для одного и того же момента времени периодичность того же типа, как и в том случае, когда мы рассматриваем электромагнитное поле в данной точке для ряда последовательных моментов времени. Впрочем, пространственная периодичность, в отличие от временной, искажается постепенным убыванием поля — или, точнее, амплитуды его колебаний — с увеличением расстояния.

Эти соотношения в простейшем случае гармонического колебательного движения данного заряда могут быть выражены формулой вида

где F обозначает электрическую или магнитную напряженность в момент t на расстоянии R от заряда, ω = 2πf = 2π/Т — «угловую частоту» его колебаний, а f(R) — функцию, характеризующую зависимость амплитуды колебаний поля от расстояния. Разность t - R/c представляет собой эффективное время t', о котором мы говорили выше и к которому относится положение заряда, действие которого определяется в момент t.

Полагая

сТ= λ,

мы можем переписать выражение

ω (t – R/c) в виде 2π (t/T – R/λ). Отсюда видно, что величина λ играет по отношению к расстоянию R такую же роль, какую период колебаний Т играет по отношению к времени t. Таким образом, для каждого момента времени формула (7) дает некоторое колебание поля в пространстве того же самого типа как и колебание во времени — если отвлечься от искажения, характеризуемого множителем f(R) — с периодом λ. Такого рода пространственные колебания называются, вообще говоря, волнами, а период их λ называется длиной волны. Картина, определяемая «фазовым множителем» sin ω ( t - R/c), представляет собой ряд концентрических сфер, характеризуемых определенными значениями «фазы»

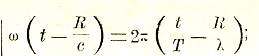
с течением времени каждая из подобных сфер непрерывно расширяется во все стороны путем увеличения ее радиуса со скоростью с. Мы получаем, таким образом, шаровые волны, распространяющиеся со скоростью с.

Эти соображения применимы в принципе к любому их тех четырех типов электромагнитных полей, которые были указаны нами выше — то есть кулоновому, био-саваровскому, фарадеевскому и максуэловскому полю. Однако, в электромагнитной теории понятие волн применяется исключительно к полям фарадей-максуэловского типа. Это объясняется тем обстоятельством, что последние убывают с расстоянием гораздо медленнее, нежели кулоновское и био-саваровское поле, а именно обратно пропорционально первой степени расстояния, а не второй степени, как последние. Таким образом, на больших расстояниях, то есть там, где волнообразный характер распространения электромагнитных колебаний становится отчетливо выраженным [благодаря сравнительно медленному убыванию амплитудного множителя f(R)], кулоновское и био-саваровское поля, преобладающие на малых расстояниях, совершенно стушевываются перед фарадей-максуэловским. При этом, под «малым» или «большим» расстоянием следует понимать расстояние R, малое или большое по сравнению с длиной волны λ = сТ. Заметим, что гармонически колеблющийся электрический заряд называется обычно электрическим вибратором, а зона, простирающаяся на расстояния R > λ — волновой зоной.

Существенное различие между полями, убывающими обратно пропорционально квадрату расстояния и первой его степени, с точки зрения представления о волнах станет нам более ясным, если мы рассмотрим вопрос о количестве энергии, связанной с полем и распространяющейся наружу или, как говорят, излучающейся вместе с ним. С этой целью рассмотрим количество энергии, заключенной между двумя соседними волновыми поверхностями одинаковой фазы, то есть двумя сферами с радиусами R и R + λ, где R = ct. Если R велико в сравнении с λ, то объем рассматриваемого слоя может быть представлен в виде 4πR²λ. Количество содержащейся в нем энергии равно произведению его на ее объемную плотность. Последняя, как мы знаем, пропорциональна квадрату напряженности поля. Таким образом, в случае кулоновского и био-саваровского поля плотность энергии обратно пропорциональна четвертой степени расстояния, так что энергия, содержащаяся в волновом слое данной толщины λ по мере его расширения (то есть распространения волн), убывает обратно пропорционально квадрату расстояния.

Мы видим, следовательно, что в этом случае говорить о переносе волнами определенной энергии невозможно. А потому, оказывается нецелесообразным вообще говорить о каких бы то ни было волнах.

Иначе обстоит дело в случае фарадей-максуэловского поля. Здесь плотность энергии оказывается обратно пропорциональной квадрату расстояния, а, следовательно, величина энергии, уносимой раздувающимся волновым слоем, — независимой от его радиуса, то есть постоянной. В этом случае представление о волнах, как о носителях электромагнитной энергии, имеет, поэтому, непосредственный физический смысл. Заметим, что аналогичным образом обстоит дело в случае звуковых волн, где амплитуда колебаний также оказывается обратно пропорциональной первой степени расстояния, а средняя плотность энергии, измеряемая силой или интенсивностью звука, обратно пропорциональной квадрату расстояния. В случае световых волн, то есть электромагнитных волн определенной длины, силе звука соответствует сила или интенсивность света, измеряемая объемной плотностью энергии электромагнитного поля. На малых (по сравнению с длиной волны) расстояниях, от закона обратной пропорциональности интенсивности квадрату расстояния должны наблюдаться отступления; однако, практически, поскольку принимаются во внимание лишь небольшие расстояния, эти отступления не играют роли.

Энергия, уносимая электромагнитными волнами, берется, очевидно, за счет их источника, то есть за счет механической энергии колеблющегося электрического заряда. Но эту механическую энергию, как мы знаем, можно рассматривать как энергию электромагнитного поля, создаваемого им и его партнером (то есть неподвижным зарядом противоположного знака, притяжением к которому обусловливается колебательное движение первого заряда). С этой точки зрения потенциальная энергия образуемой ими системы (включая собственную энергию каждого из зарядов в отдельности) измеряется электрической энергией кулоновского поля, а кинетическая энергия — магнитной энергией био-саваровского поля. Таким образом, механическую энергию можно рассматривать как электромагнитную энергию, сосредоточенную в непосредственной близости к данному заряду (и его партнеру), то есть на расстоянии меньшем, нежели длина волны. Что касается всей остальной электромагнитной энергии, находящейся в волновой зоне и непрерывно уносимой волнами во все стороны, то для нее в механике нет аналога. Она пропорциональна квадрату ускорения движущегося заряда, а также толщине волновой зоны, то есть времени, протекшему с начала рассматриваемого движения. Эту энергию называют обычно лучистой энергией, а процесс превращения механической энергии (то есть энергии кулоновского и био-саваровского поля) в лучистую (то есть в энергию фарадей-максуэловского поля) называют электромагнитным излучением. Следует подчеркнуть, что приведенное деление электромагнитной энергии на механическую и лучистую не может быть проведено точным образом и поэтому имеет весьма условный смысл, хотя и оказывается весьма удобным на практике. Исторически оно возникло и развилось на почве представления об эфире как о передатчике «лучистых явлений» (то есть видимого и невидимого света), причем в этой теории лучистая энергия приписывалась эфиру, а механическая — обыкновенной материи.

До сих пор мы ограничивались весьма суммарным описанием фарадей-максуэловского поля, или поля электромагнитных волн, отметив лишь тот факт, что напряженность этого поля прямо пропорциональна ускорению создающего его заряда и обратно пропорциональна первой степени расстояния. В дополнение к этому мы должны теперь указать следующие его особенности.

1) Поперечный характер, выражающийся в перпендикулярности электрической напряженности и магнитной к направлению «луча», то есть прямой, проведенной от очага поля к данной точке и определяющей направление распространения волн в этой точке. К этому следует прибавить, что зависят не от всего вектора ускорения, но лишь от поперечной проекции его на плоскость, перпендикулярную к лучу, причем вектор направлен в сторону противоположную ускорению.

2) Напряженности численно равны друг другу и взаимно перпендикулярны. При этом они направлены таким образом, что  при вращении от (на 90°) правый винт передвигается в направлении луча.

Если изобразить рассматриваемое поле на некотором расстоянии R от заряда при помощи силовых линий, то получается следующая картина. Силовые линии образуют сетку, лежащую на поверхности шара с радиусом R. Если уподобить этот шар земному шару и под осью его подразумевать прямую, проведенную в направлении ускорения (в эффективный момент t’ = t - R /с), то электрические силовые линии образуют меридианы шара, расходящиеся от положительного (северного) полюса и сходящиеся к отрицательному (южному), а магнитные силовые линии — параллельные круги, проведенные с запада на восток, то есть так, чтобы при вращении в этом направлении правый винт перемещался в направлении оси. Наконец, густота силовых линий — как электрических, так и магнитных — достигает максимума у экватора и обращается в нуль у полюсов.

Заметим, что магнитное поле, о котором идет речь и которое мы называли выше «максуэловским», имеет структуру, совершенно аналогичную био-саваровскому полю — как в смысле формы силовых линий (коаксиальные круги), так и в смысле их густоты на данном расстоянии. При этом роль скорости играет ускорение, а густота убывает с расстоянием обратно пропорционально первой, а не второй степени.

Что касается фарадеевского электрического поля, то оно имеет характер совершенно отличный от кулоновского. Оно действует в сторону, противоположную ускорению создающего его заряда на все одноименные заряды, окружающие последний. В случае ускоренно-движущегося электрона, фарадеевское взаимодействие (взаимная индукция) его элементов создает силу торможения, которую мы интерпретируем как силу инерции. Учитывая запаздывание элементарных сил, исходящих от отдельных элементов заряда электрона, нетрудно показать, во-первых, что масса его должна возрастать с увеличением скорости, обращаясь в бесконечность при приближении последней к скорости света (причем это увеличение массы оказывается пропорциональным кинетической энергии электрона). Далее, это запаздывание приводит к тому, что к силе инерции присоединяется добавочная сила, имеющая характер трения (сила лучистого торможения); действием этой силы и обусловливается то уменьшение механической энергии электрона, которым сопровождается его электромагнитное излучение.

Мы видим, таким образом, что электрические силы, которыми обусловливается инерция материи, по существу тождественны с силами, образующими световые волны.

§ 3. Электромагнитные волны и их источники. Колебательный или волновой характер световых явлений был установлен задолго до появления электромагнитной теории света в связи с явлениями интерференции (и дифракции), которые вместе с тем дали возможность измерить длину световых волн. Последняя, как известно, заключается в пределах примерно от 8 стотысячных долей сантиметра для красного света и до 4 стотысячных — для фиолетового, чему соответствует громадная частота колебаний — порядка нескольких сот биллионов в секунду.

Теория Максуэла поставила на очередь создание и обнаружение искусственных электромагнитных колебаний гораздо меньшей частоты и соответственно этому гораздо большей длины волны. Эта задача была блестяще решена Герцем в начале 1880-ых годов, а двадцатью годами позже открытые Герцем электромагнитные волны были технически использованы Маркони (а отчасти в России Поповым) для телеграфирования без проводов (см. радиотехника, XXXV, 362 сл.).

Длина электромагнитных волн, применяемых в радиотелеграфии, до последнего времени измерялась сотнями метров или даже километрами. Таким образом, между волнами видимого света и радиоволнами лежала целая пропасть. В настоящее время, однако, эта пропасть почти уничтожена. С одной стороны, длину искусственно создаваемых электромагнитных волн удалось путем уменьшения соответствующих приборов-вибраторов уменьшить с сотен метров до нескольких сантиметров и даже до десятых долей миллиметра. С другой стороны, чисто оптические исследования были продолжены за пределы красного конца спектра в область инфракрасных лучей (раньше называвшихся тепловыми), причем удалось практически осуществить «смычку» этих лучей с электромагнитными. Заметим, что одновременно с необычайным расширением представления о световых волнах в сторону длинных волн было достигнуто не меньшее расширение его в противоположную сторону необычайно коротких волн, путем открытия рентгеновых лучей. (см.). Последние образуют непрерывную гамму, заканчивающуюся длиной волны примерно около одной миллиардной сантиметра. Волновая природа рентгеновых лучей, их принципиальная тождественность с видимыми лучами, а, следовательно, и с электромагнитными волнами Герца, была установлена не сразу, а лишь примерно лет через 20 после их открытия, когда Лауе (в 1913 г.) впервые удалось обнаружить явления интерференции рентгеновых лучей при прохождении их через кристаллы или отражении от последних. Явление интерференции света заключается в периодическом усилении и ослаблении волн одинаковой длины при наложении их друг на друга. Подобные ряды волн образуются при отражении рентгеновых лучей от равноотстоящих плоскостей, образуемых атомами кристалла, причем усиление их происходит лишь при определенных углах падения (и отражения), при которых волны, отраженные от соседних плоскостей, отличаются друг от друга по фазе на одну или несколько длин волн. Особая пригодность именно кристаллов для наблюдения интерференции рентгеновых лучей обусловливается тем обстоятельством, что расстояние между соседними плоскостями (или атомами) у большинства кристаллов совпадает по порядку величины с длиной волны рентгеновых лучей.

Явление интерференции рентгеновых лучей оказалось мощным орудием экспериментального исследования строения материальных тел — в особенности твердых, и в последнее время получило ряд важнейших применений в технологии и испытании материалов.

Спектр «световых» колебаний (в расширенном смысле слова) простирается в сторону коротких волн еще довольно далеко за пределы рентгеновых лучей. Соответствующие ультра-рентгеновые лучи, испускаемые некоторыми радиоактивными веществами, называются гамма-лучами; лучи еще более короткой волны, в тысячу раз меньшей, чем у крайних рентгеновых лучей, пронизывают все мировое пространство и воспринимаются на земле как «космическое излучение». Космические лучи вызывают ионизацию верхних слоев атмосферы, то есть вырывание электронов из атомов или молекул воздуха, благодаря чему последний приобретает способность проводить электричество. В этом отношении, то есть в повышении ионизации, а следовательно и электропроводности воздуха, космическим лучам помогают ультрафиолетовые лучи Солнца, действие которых ограничивается, конечно, только обращенной к Солнцу половиной земного шара.

Электропроводность верхних слоев атмосферы имеет чрезвычайно существенное значение для распространения электромагнитных волн, применяемых в радиотехнике, на большие расстояния вдоль земной поверхности. Проводящие слои воздуха отражают эти волны примерно так же, как и земная поверхность; и вместо того, чтобы уноситься в мировое пространство, радиоволны, запертые между поверхностью земного шара и его воздушным чехлом, огибают землю без заметного ослабления. Таким образом, между самыми короткими и самыми длинными электромагнитными волнами существует весьма своеобразная связь; а именно: первые (ультрафиолетовые и космические лучи) способствуют распространению вторых (радиоволны) вдоль земной поверхности. Необходимо отметить, что в положении «наибольшего благоприятствования» находятся так называемые «короткие» радиоволны от 40 и примерно до 8 метров. Более длинные волны проходят через ионизованные слои атмосферы беспрепятственно; более короткие, наоборот, поглощаются в них; и лишь волны, длина которых лежит в указанном интервале, возвращаются обратно к земной поверхности.

Источником электромагнитных волн служит колебательное движение электрических зарядов. В случае радиоволн это колебательное движение осуществляется в форме переменных электрических токов высокой частоты примерно от 1 и до 100 миллионов колебаний в секунду. Возможность подобных колебаний, еще до открытия сопровождающего их «электромагнитного излучения», была установлена теоретически В. Томсоном (лорд Кельвин). Томсон исходил при этом из схемы, изображенной на рис. 19, то есть конденсатора, обкладки которого соединены друг с другом с наружной стороны проволокой. Последняя для увеличения самоиндукции обычно закручивается в спираль (соленоид), так что предыдущая схема принимает вид, изображенный на рис. 21.

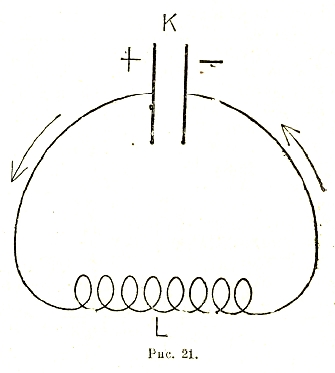
Рис. 21.

Разрядка конденсатора осуществляется, как мы уже видели, в форме электрического тока, который, однако, не прекращается в тот момент, когда конденсатор совершенно разрядился, но продолжает течь по инерции (т. е. благодаря самоиндукции), перезаряжая конденсатор и в результате постепенно ослабевая до тех пор, пока конденсатор не зарядится до (приблизительно) первоначальной разности потенциалов, но в противоположном смысле. Затем ток начинает течь в обратную сторону до тех пор, пока конденсатор вновь не перезарядится и таким образом вернется в исходное состояние. При этом сила тока достигает максимума в тот момент, когда заряд обкладок конденсатора обращается в нуль.

Происходящие таким образом электрические колебания совершенно аналогичны колебательному движению груза, подвешенного на пружине, если вывести его из равновесия (путем толчка или изменения длины пружины). Заряжению или перезаряжению конденсатора соответствует сжатие или растяжение пружины, а силе тока — скорость движения груза. Колебания груза можно рассматривать как непрерывное превращение его потенциальной энергии в кинетическую и обратно. Точно так же электрические колебания рассматриваемого нами типа можно трактовать как непрерывный переход электрической энергии конденсатора в магнитную энергию тока и обратно. Электрическая энергия (играющая в этом случае роль потенциальной) может быть выражена через заряд одной из обкладок е и емкость С формулой а магнитная — через силу тока і и коэффициент самоиндукции L формулой 1/2 Li². Приравнивая друг к другу максимальные значения этих энергий е₀²/2С и 1/2 L i₀² и принимая во внимание, что в силу соотношения

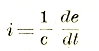
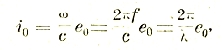
где f — частота колебаний, а λ = с/f — длина соответствующих электромагнитных волн (см. ниже), мы получаем следующую формулу (впервые выведенную Томсоном):

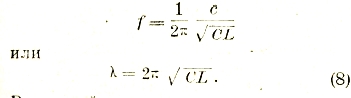
В этих формулах емкость и самоиндукция выражены соответственно в электрических и электромагнитных единицах, то есть в сантиметрах, так что длина волны λ также получается в сантиметрах. Обычно C и L имеют тот же порядок величины, как и линейные размеры проводника (поскольку форма последнего не выбрана нарочито таким образом, чтобы по возможности увеличить значения C и L). При таких условиях длина электромагнитных волн, излучаемых полупроводником при наличии электрических колебаний, должна быть также близка к его линейным размерам.

Колебание груза, подвешенного на пружине, является прототипом колебательного движения, которое способны совершать все решительно упругие тела — струны, стержни, пластинки и т. д., вообще тела любой формы и размеров. В этом случае роли пружины и груза оказываются совмещенными в одном и том же теле (им может быть, в частности, пружина, лишенная дополнительного груза, помимо своей собственной массы).

Аналогичным образом электрические колебания описанного выше типа могут происходить в любом металлическом теле, без дополнительной самоиндукции в виде соленоида и дополнительной емкости в виде конденсатора, каковы бы ни были его размеры и форма. При этом, так же как и в случае упругих колебаний, частота их оказывается тем больше, чем меньше линейные размеры тела. Необходимо отметить, что в обоих случаях могут иметь место колебания различных частот. В простейшем случае струны или длинного провода эти частоты находятся друг к другу в отношении ряда целых чисел 1:2:3 и т. д., образуя основной тон, или основное колебание (самое медленное), и верхние дополнительные колебания (или обертоны).

Таким образом, всякое металлическое тело способно совершать, наряду с упругими колебаниями, воспринимаемыми в форме звука, электрические колебания, не воспринимаемые непосредственно, но являющиеся по существу не чем иным, как невидимым светом чрезвычайно большой длины волны. Длина электромагнитных волн, испускаемых подобным «святящимся», то есть электрически вибрирующим телом, приблизительно совпадает с длиной звуковых волн, соответствующих упругим колебаниям этого тела, и в случае основного колебания сравнима с его линейными размерами. Так, например, основному колебанию металлического провода, как упругому (звуковому), так и электрическому (световому), соответствует длина волны (звуковой или электромагнитной), ровно вдвое большая его собственной длины. Это соотношение объясняется тем, что в обоих случаях концы провода являются «узловыми» точками (в которых амплитуда колебаний равна нулю) и что расстояние между двумя соседними узлами равняется половине длины волны.

При данной длине волны λ частота колебаний, то есть число колебаний в секунду f, тем больше, чем больше скорость их распространения; последняя может быть определена как произведение f на λ. Принимая во внимание, что скорость звука (то есть скорость распространения упругих колебаний) измеряется несколькими сотнями метров или максимум несколькими километрами в секунду, тогда как скорость света (электромагнитных волн) равна 300 000 км в секунду, мы приходим к заключению, что у одного и того же (металлического) тела частота электрических (световых) колебаний должна быть примерно в 100 тысяч раз больше, чем частота колебаний звуковых. Так, например, в случае проволоки в 1 метр длиной мы должны получить, при длине волны в 2 метра, звуковые колебания с частотой порядка 1 000 и «световые» колебания с частотой порядка 100 миллионов в секунду.

«Звучание» упругого тела может быть вызвано простым толчком или ударом. При этом колебательное движение тела быстро замирает или, как говорится, «затухает», отчасти вследствие «излучения» его энергии в виде звуковых волн, распространяющихся в окружающем воздухе, отчасти же вследствие превращения этой энергии в теплоту (нагревание). Аналогичным образом невидимое «свечение» металлического тела может быть вызвано особым «электрическим толчком», причем колебательное движение, образующее сущность этого свечения, чрезвычайно быстро затухает, частью благодаря излучению энергии в окружающее пространство («эфир») в виде электромагнитных волн, частью же вследствие превращения ее в тепловую энергию (тепловое действие тока, джоулево тепло).

Электрический толчок, о котором идет речь, может быть вызван множеством различных способов, например, введением рассматриваемого тела в разрядную цепь индукционной катушки. Именно таким способом пользовался Герц; аналогичным образом действовал и Маркони. Впоследствии, однако, в радиотехнике от затухающих электрических колебаний перешли к колебаниям незатухающим, которые возбуждаются не отдельными толчками, а непрерывным воздействием, аналогичным действию смычка на струну. В качестве подобного возбудителя или генератора незатухающих электрических колебаний вначале служила электрическая дуга; в последнее время выработалась новая универсальная форма «электрического смычка» в виде так называемого триода, или катодной лампы с тремя электродами (см. электронная лампа). Пользуясь подобным электрическим смычком, можно «играть» на любом металлическом теле неслышимые и невидимые световые симфонии.

В радиотехнике источниками «света», то есть невидимых электромагнитных волн, служат передатчики или передаточные антенны, достигающие иногда (в случае очень длинных волн) гигантских размеров. Источниками видимого света (а также примыкающих к нему инфракрасных и ультрафиолетовых лучей), то есть электромагнитных волн с длиной порядка нескольких стотысячных долей сантиметра, служат отдельные атомы и молекулы материальных тел. Эти миниатюрные радиоантенны имеют чрезвычайно маленькие размеры — примерно в 10 тысяч раз меньшие, чем длина испускаемых ими волн. При этом под размерами их понимаются размеры тех орбит, по которым движутся находящиеся в них электроны. Эти размеры могут быть приблизительно определены из расстояний между соседними атомами в твердых телах; в случае наружных электронов они близки к 10^-8, то есть одной стомиллионной сантиметра.

Заметим, что наличие в мельчайших частицах нейтральной материи – атомах — еще более мелких наэлектризованных частиц непосредственно явствует из самого факта видимости материальных тел, ибо эта видимость обозначает не что иное, как испускание электромагнитных волн, источником которых могут быть лишь колеблющиеся наэлектризованные частицы. Природа этих частиц может быть установлена более точным образом путем изучения того изменения в характере испускаемого света, которое вызывается действием внешнего магнитного поля. Это изменение, которое искал еще Фарадей, было обнаружено в 1900 году Земаном. В простейших случаях оно заключается в расщеплении каждой спектральной линии на три компоненты, из коих центральная совпадает с исходной линией, а боковые смещены в противоположные стороны на расстояния, пропорциональные напряженности поля (см. земаново явление и энергия). Теория этого «явления Земана» была дана Лоренцом. По существу она совпадает с изложенной в предыдущей главе ланжевеновской теорией диамагнетизма. Действие магнитного поля на колеблющийся или обращающийся вокруг центра атома электрон сводится, как мы видели, к прецессии его орбиты, то есть к сравнительно медленному вращению ее вокруг направления магнитного поля. При этом гармоническое колебательное движение, параллельное полю, не испытывает изменения, то есть сохраняет свою нормальную частоту f, тогда как прямолинейное гармоническое колебание в направлении, перпендикулярном к полю благодаря прецессии, перестает быть гармоническим и может быть представлено в виде геометрической суммы двух вращений одинаковой амплитуды и противоположного направления е частотами f + f₁ и f - f₁, где f — частота невозмущенного колебания, а f₁ – частота прецессии, пропорциональная интенсивности магнитного поля. Это изменение в характере колебательного движения отражается на характере испускаемого света в виде расщепления исходной неполяризованной спектральной линии на три поляризованные компоненты — одну прямолинейно поляризованную с неизменной частотой и две поляризованные по кругу в противоположные стороны с частотами f + f₁ и f - f₁ (см. поляризация света и энергия). По направлению поляризации смещенных компонент, а также по величине их смещения f₁ можно определить, во-первых, знак электрического заряда колеблющейся частицы и, во-вторых, отношение этого заряда к массе. Таким путем оказалась возможность отождествить внутриатомные частицы, колебаниями которых обусловлен испускаемый атомами свет, с электронами, наблюдавшимися ранее в свободном состоянии в виде катодных лучей.

При падении на атомы какого-либо тела свободные электроны, образующие катодные лучи, вызывают колебательное движение связанных внутриатомных электронов, вызывая, таким образом, свечение атомов. Сравнительно медленные катодные лучи, с энергией, соответствующей ускоряющей разности потенциала в несколько вольт, приводят при этом в колебание наименее прочно связанные внешние электроны, от которых зависит видимый, а также отчасти инфракрасный и ультрафиолетовый свет. Более быстрые катодные лучи с энергией порядка нескольких тысяч или десятков тысяч вольт приводят в колебание более прочно связанные внутренние электроны, которыми обусловливается испускание рентгеновых лучей.

Необходимо отметить, что и при отсутствии внешнего воздействия находящиеся в атоме электроны не покоятся, но быстро обращаются вокруг положительных ядер. Однако, это нормальное движение, вопреки развитым выше представлениям, столь хорошо применимым к электрическим колебаниям в обыкновенных проводниках, не сопровождается излучением. Связанные с этим затруднения привели к созданию теории квантов (см. энергия).

§ 4. Вынужденные электрические колебания и вторичные электромагнитные полны; распространение световых волн в материальных телах. В предыдущем параграфе мы рассматривали электромагнитные волны как следствие электрических колебаний, то есть колебательного движения электронов. Последние могут быть, однако, не только причиной, но и следствием первых. Если какое-нибудь тело находится в поле электромагнитных волн, исходящих от внешнего источника, то образующие эти волны колеблющиеся электрические (и магнитные) силы вызывают вынужденные колебания электронов в этом теле. Эти вынужденные электрические колебания происходят синхронно с вызывающими их силовыми колебаниями, то есть имеют одинаковую с ними частоту. Будучи следствием «первичных» силовых (электромагнитных) колебаний, они являются в свою очередь причиной или источником «вторичных» силовых колебаний, то есть вторичных электромагнитных волн той же самой длины.

Рассеянный и отраженный свет, благодаря которому мы видим окружающие нас несамосветящиеся тела, является примером вторичных электромагнитных волн, испускаемых по вышеописанному механизму. При падении на тело монохроматического света, то есть света, образованного синусоидальными волнами, тело представляется окрашенным в тот же самый цвет, как и источник света, что соответствует совпадению длины первичных и вторичных волн. Таким образом, в этом случае различные тела отличаются друг от друга лишь яркостью своего вторичного свечения, то есть интенсивностью рассеянного или отраженного света по отношению к падающему. Эта относительная интенсивность тем больше, чем больше амплитуда электронных колебаний, вызываемых первичными силовыми колебаниями данной амплитуды. В том случае, когда электроны способны совершать свободные колебания определенной частоты f₀, амплитуда их вынужденных колебаний оказывается тем большей, чем ближе частота f вынуждающих колебаний к f₀. Если пренебречь силами трения, то амплитуда вынужденных колебаний изменяется обратно пропорционально разности f² - f₀²,обращаясь в бесконечность при f = f₀. На самом деле благодаря силам трения она при этом остается конечной, достигая более или менее резко выраженного максимума.

Это явление, хорошо известное в акустике, называется резонансом. Разнообразная окраска, которую принимают разные тела при освещении одним и тем же белым светом, объясняется неодинаковой интенсивностью отражения различных монохроматических составляющих этого света.

В особенно отчетливой форме явление оптического резонанса наблюдается в случае газов: при пропускании через какой-нибудь холодный (т. е. не самосветящийся) газ смешанного (белого) света поглощаются лишь те лучи, которые могут испускаться этим газом в раскаленном состоянии или под влиянием электрического разряда (т. е. электронных ударов). Другими словами, «спектр поглощения» газа совпадает с его спектром испускания.

В области длинных электромагнитных волн, применяемых в радиотехнике, мы имеем дело с явлением вторичных или вынужденных электрических колебаний при приеме радиоволн. Для улучшения приема, то есть максимального увеличения интенсивности вынужденных колебаний, применяется принцип резонанса. Последний достигается путем настройки приемной системы, то есть приближения частоты f₀ ее свободных колебаний к частоте f первичных силовых колебаний, которые в этом случае воспринимаются в виде некоторой внешней электродвижущей силы.

Эффективное сопротивление колебательного контура, то есть отношение амплитуды тока i₀ к амплитуде электродвижущей силы f₀ выражается при наличии самоиндукции L и емкости С формулой

которая при С = 0 переходит в формулу (33) предыдущей главы. Эта формула показывает, что электродвижущая сила самоиндукции и разность потенциалов на обкладках конденсатора действуют в противоположных направлениях, ослабляя друг друга. При условии

они взаимно компенсируются, что соответствует минимальному значению эффективного сопротивления R‘ = R, то есть максимальной силе тока. Это условие, как показывает формула (7), в связи с ω = 2πf представляет собой условие резонанса.

При рассеянии монохроматического света обычно наблюдается частичное изменение частоты колебаний. Другими словами, в спектре рассеянного света, наряду с «линией», характеризующей первичные лучи, наблюдаются сравнительно очень слабые линии, которым соответствует несколько отличная частота колебаний.

Это явление, предвиденное еще Рэлеем в начале нашего века, было впервые экспериментально открыто в 1928 году почти одновременно Раманом в Калькутте и у нас в СССР Л. И. Мандельштамом и Г. С. Ландсбергом (см. раманово явление и энергия). В радиотехнике ему соответствует широко известное явление модуляции (незатухающих) электрических колебаний, то есть периодическое изменение их интенсивности. Представим себе, например, что на передаточной станции создаются колебания с частотой f = 1 миллион, амплитуда которых периодически усиливается и ослабляется, f₁ = 1000 раз в секунду, под действием, например, телефонной мембраны, колеблемой соответствующим звуком. Это колебание переменной амплитуды можно рассматривать как сумму двух колебаний с постоянными амплитудами, но с различными частотами, равными f + f₁ и f – f₁¹). Соответственно этому испускаемые станцией электромагнитные волны можно рассматривать как результат наложения двух систем волн, с частотами f + f₁ и f – f₁. Если приемную станцию настроить на одну из них, то при наличии очень острого резонанса другая система не будет вовсе восприниматься.

В случае электромагнитных волн, рассеиваемых двухатомными или более сложными молекулами (а также кристаллами), которые мы будем при этом рассматривать не как радиоприемники, но как радиопередатчики (радиоприемником служит при этом спектральный аппарат), происходит совершенно аналогичное явление модуляции, обусловленное вращательным и колебательным движением молекул (так как амплитуда электронных колебаний зависит от расстояния между атомами и вообще от их относительного положения).

 

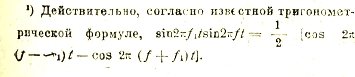
Таким образом, в спектре рассеянного света наряду с неизмененными лучами должны наблюдаться лучи, частота которых отличается от частоты первичных лучей на частоту свободного колебательного движения атомов в молекуле или на число ее оборотов (в секунду) вокруг собственной оси. Эти результаты, а равно и все вытекающие из них следствия относительно интенсивности рассеянных лучей находятся в полном согласии с опытом.

Возвращаясь к радиоволнам, мы должны отметить, что при приеме их непосредственно наблюдается не основная передающая частота f, но только лишь частота модуляции f₁, которая обычно лежит в акустической области и может быть слышима в телефон. Это устранение передающей частоты осуществляется путем так называемого выпрямления электрических колебаний в приемном аппарате. Выпрямление осуществляется тем, что через цепь приемника электрический ток может проходить в одну лишь сторону, тогда как при противоположном направлении электродвижущей силы тока не получается. Таким образом, выпрямитель представляет собой своего рода электрический клапан, или «вентиль», напоминающий по своему действию клапан обыкновенного воздушного или водяного насоса; при одном направлении струи воздуха (или воды) этот клапан остается открытым, а при противоположном — он захлопывается. Простейшими выпрямителями в радиотехнике являются кристаллические детекторы хорошо известные каждому радиолюбителю. Более совершенными и тонкими выпрямителями являются те же катодные лампы (триоды), которыми пользуются и для генерации электрических колебаний.

Если в телефоне радиоприемника одновременно возбуждаются два электрических колебания с весьма высокими, но сравнительно близкими частотами f₁ и f₂, то, складываясь друг с другом, или, как говорится, интерферируя, они попеременно то усиливают, то ослабляют друг друга. Число подобных усилений или ослаблений — или так называемых биений — равно разности обеих частот f₁ – f₂. Если эта разность лежит в акустической области, то есть составляет несколько сотен или тысяч в секунду, то биения непосредственно воспринимаются слухом, как «разностный» тон соответствующей высоты, между тем как оба интерферирующих колебания, образующих этот тон, остаются совершенно незаметными. Само собой разумеется, что для обнаружения их биений они должны быть выпрямлены.

На этом принципе (впервые использованном английским физиком Виддингтоном для измерения очень маленьких изменений емкости) основан построенный Л. С. Терменом «радиофон» («терменовокс») — музыкальный прибор, на котором можно «играть» путем простого движения руки, без непосредственного соприкосновения с ним. Прибор состоит из двух колебательных контуров, причем частота колебаний одного из них (f₁) остается постоянной, а другого (f₂) меняется при приближении или удалении руки от стержня, связанного с его емкостью (конденсатором). Таким образом, движением руки мы меняем, и притом чрезвычайно быстро, частоту разностного тона f₁ - f₂, издаваемого мембраной телефона, на который действуют оба колебания (см. электрические музыкальные инструменты, LII, 8 и рис. 1).

Описанный выше эффект Рамана можно, если угодно, рассматривать как аналог подобного рода биений в оптической области, то есть в области видимого света. Здесь основными колебаниями являются быстрые первичные колебания (f) и медленные колебания, образующие модуляцию (f₁). При этом, однако, наряду с разностным «тоном» f – f₁, наблюдается и суммовый с частотой f + f₁.

Мы должны теперь вкратце рассмотреть вопрос о распространении электромагнитных и в частности световых волн в материальных телах. Это распространение представляет собой сложный процесс, заключающийся в непрерывном возбуждении первичными электромагнитными колебаниями вторичных и слиянии последних с первыми при дальнейшем совместном их распространении в теле. Если бы содержащиеся в теле электроны были связаны абсолютно прочно, то есть не могли приводиться в колебание первичными волнами, то последние распространялись бы совершенно таким же образом, как если бы тела вовсе не было, то есть как в пустоте. Изменение характера их распространения в материальной среде по сравнению с пустотой обусловливается именно тем обстоятельством, что раскачивая электроны, содержащиеся в теле, электромагнитные волны, вызывающие эти колебания, непрерывно видоизменяются путем слияния с волнами, вызываемыми последними.

В том случае, когда колебательное движение электронов происходит гармонически (синусоидально) и притом без трения, результатом всего процесса является кажущееся изменение — обычно уменьшение — длины волны, тем большее, чем больше подвижность электронов, то есть чем больше диэлектрическая постоянная среды εf для колебаний данной частоты f. Отношение истинной длины волны λ₀ = с/f («в пустоте») к кажущейся λ равно, как показал впервые Максуэл, квадратному корню из этой диэлектрической постоянной. Если, как это делается обычно, определить произведение λf = v как скорость распространения волн в данной среде, то соотношение между длинами волн можно заменить соотношением между скоростями в пустоте и в среде и положить

С другой стороны, как известно из элементарной теории преломления волн на поверхности двух различных сред, отношение с/v должно равняться отношению синуса угла падения к синусу угла преломления, то есть показателю преломления данной, среды по отношению к пустоте. Таким образом, согласно электромагнитной теории Максуэла, показатель преломления какого-либо тела оказывается равным квадратному корню из его диэлектрической постоянной для колебаний рассматриваемой частоты. Последняя оговорка при первоначальных проверках теории Максуэла не принималась во внимание, так что показатель преломления для света с данной частотой колебаний сравнивался с диэлектрической постоянной тела в постоянном электрическом поле. Этим обстоятельством объясняются те кажущиеся отступления от соотношения Максуэла, которые были найдены первыми исследователями. При учете зависимости диэлектрической постоянной от частоты колебаний f (так называемой «дисперсии») соотношение Максуэла выполняется совершенно точно.

Необходимо подчеркнуть, что обычное представление о скорости v = λf, как об истинной скорости электромагнитных волн в данной среде, в корне неправильно. Истинная скорость электромагнитных волн в любой материальной среде та же самая, что и в пустоте; величина же v представляет собой кажущуюся скорость, и, строго говоря, имеет смысл только для гармонических колебаний.

Наличие сил трения, тормозящих колебательное движение электронов, проявляется в том, что результирующие волны, получающиеся от слияния волн, вызывающих это движение и им вызываемых, испытывают при распространении в теле постепенное уменьшение интенсивности или, как говорится, поглощение (помимо этого, силы сказываются также на величине кажущейся длины волны, а, следовательно, и кажущейся скорости распространения).

Аналогичным образом объясняются разные другие эффекты, наблюдающиеся при распространении электромагнитных волн в материальной среде, как, например, открытое еще Фарадеем явление вращения плоскости поляризации световых лучей, то есть направления колебаний при распространении их в продольном магнитном поле. Обусловливаемая последним прецессия сказывается в том, что под влиянием электрических сил, колеблющихся в одной плоскости, электроны совершают вынужденные колебания в несколько отличной плоскости, в результате чего плоскость колебаний постепенно поворачивается вокруг магнитных силовых линий.

§ 5. Математическая формулировка электромагнитной теории Максуэла-Лоренца. Результаты, изложенные в последних двух главах, могут быть сформулированы в виде системы дифференциальных уравнений электромагнитного поля, представляющих собой обобщение и дальнейшее развитие уравнений электрического поля, рассмотренных в конце I главы.

При выводе этих уравнений, впервые установленных Максуэлом и приведенных к окончательному виду Лоренцом, мы будем исходить из уравнений § 1 настоящей главы, определяющих «магнитодвижущую силу» V’ электрического тока проводимости и смещения:

и электродвижущую силу индукции

Заметим, прежде всего, что величины i, Ψ и Ф в правых частях этих уравнений представляют собой потоки (электрического заряда, электрического поля и магнитного поля), проходящие через какую-либо поверхность S, ограниченную тем замкнутым контуром σ, для которого вычисляется магнито- или электродвижущая сила. Потоки, не охватываемые этим контуром, не влияют на величину V или V' и могут, поэтому, не приниматься во внимание.

Обозначая вектор нормали к поверхности S (форма которой остается произвольной) через, мы можем представить потоки i, Ψ, Ф в виде

где j_n, Е_n, H_n — проекции плотности электрического тока, электрической напряженности и магнитной напряженности на нормаль. Величины V и V’ могут быть представлены аналогичным образом в виде интегралов

взятых вдоль замкнутого контура σ; здесь представляет собой вектор, направленный по касательной к σ в ту сторону, куда нужно вращать правый винт для того, чтобы он перемещался в направлении нормали.

Согласно теореме Стокса, предыдущие интегралы могут быть преобразованы в поверхностные интегралы вида

то есть в потоки через поверхность S векторов

Напомним, что вектор

определяется через свои прямоугольные слагающие формулами [гл. 1, ф. (32)]:

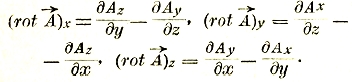
При этом в качестве поверхности S можно выбрать ту же самую поверхность, как и при определении потоков i, Ψ, Ф.

Таким образом, равенства I и II могут быть переписаны в следующем виде:

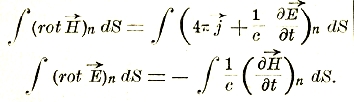
В виду произвольности поверхности S из этих равенств вытекают дифференциальные уравнения:

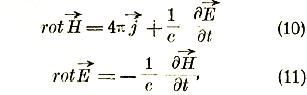
которые в проекциях на координатные оси принимают вид:

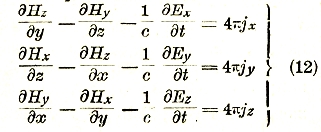
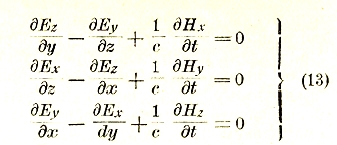
Заметим, что эти уравнения могут быть получены непосредственно из равенств I и II путем надлежащего выбора контура σ и поверхности S. А именно, в качестве σ нужно было бы выбрать бесконечно малый прямоугольный контур со сторонами, параллельными двум из координатных осей и, следовательно, с площадью S, перпендикулярной к третьей оси.

Заметим, что уравнение (11) представляет собой обобщение уравнения электростатики rot

в которое оно превращается в случае поля, не зависящего от времени.

Другое уравнение электростатики

(ср. I главу, § 8), не содержащее времени, остается в силе и в общем случае. К этому уравнению мы можем присоединить аналогичное уравнение для магнитного поля

Замена плотности ρ нулем соответствует отсутствию магнитных полюсов, которые являлись бы началом или концом магнитных силовых линий.

В проекциях на координатные оси предыдущие уравнения имеют вид:

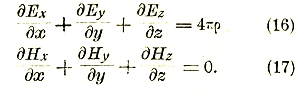
Эти уравнения совместно с (12) и (13) составляют полную систему уравнений Максуэла-Лоренца.

Заметим, что из (12) и (16) вытекает следующее соотношение между плотностью заряда и тока:

выражающее принцип сохранения электрического заряда. В самом деле, умножая это уравнение на dv и интегрируя по какому-либо объему v, мы получаем с помощью формулы Гаусса

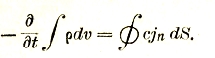
Здесь левая часть представляет собой уменьшение электрического заряда, содержащегося внутри поверхности S за единицу времени, а правая — поток электрического заряда, вытекающий за то же время через S.

Помимо соотношения (18), величины ρ и остаются совершенно произвольными и служат исходными данными при определении поля путем интегрирования уравнений Максуэла-Лоренца.

Это интегрирование облегчается введением так называемых «потенциалов» — скалярного V и векторного по формулам

Подставляя эти выражения в уравнения (11) и (15), нетрудно проверить, что они удовлетворяются тождественно (чем и оправдывается введение потенциалов), между тем, как уравнения (10) и (14) обращаются в дифференциальные уравнения второго порядка для потенциалов V и:

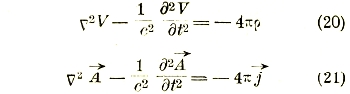
При дополнительном условии

которое выполняется в связи с соотношением (18).

Уравнение (20) представляет собой обобщение уравнения Пуассона (33) гл. I и называется уравнением Даламбера.

При ρ = 0 оно принимает вид обыкновенного волнового уравнения, то есть уравнения распространения колебаний в упругой однородной среде, причем коэффициент с обозначает скорость этого распространения.

Общие решения уравнений (20) и (21) выражаются следующими формулами:

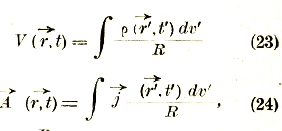
где t' = t - R/c, а R — расстояние между точкой (с радиусом-вектором), для которой определяется потенциал, и элементом объема dv (с радиусом-вектором), к которому относится плотность заряда или тока ρ,.

Таким образом, плотности эти берутся не для того момента, для которого определяется потенциал, а для предшествующего момента в соответствии с конечной скоростью распространения электромагнитных действий.

Формулы (23) и (24) можно рассматривать как общее математическое выражение этого запаздывания. Заметим, что определяемые им потенциалы также называются «запаздывающими», или «отстающими».

В применении к случаю электрического заряда е весьма малых размеров (в пределе точечного), движущегося со скоростью (которая может произвольным образом изменяться с временем) формулы (23) и (24) дают

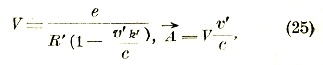
где штрихи означают, что соответствующие величины — расстояние R, скорость и проекция ее на — берутся не для момента t, для которого определяются потенциалы, но для предшествующего момента t’ = t – R’/c. Заметим, что формулы (25) были впервые даны Льенаром и Вихертом.

Из этих формул с помощью (19) можно вывести выражения для напряженностей.

Они оказываются довольно сложными и сводятся к уже рассмотренным нами выше кулоновскому-фарадеевскому полю в случае и био-саваровскому-максуэловскому в случае

Связь между слагающими электромагнитного ноля и величинами (которые характеризуют расположение и движение зарядов, т. е. материю), устанавливаемая уравнениями Максуэла-Лоренца, может быть интерпретирована двояким образом.

В первой интерпретации материя рассматривается как первичный фактор, или «причина», а электромагнитное поле — как вторичный фактор, или «следствие». Математически это означает, что величины и ρ считаются данными (известными), а величины — подлежащими определению. Во второй интерпретации, наоборот, поле считается первичным фактором, а материя вторичным — местом сгущения силовых линий поля.

Развитие электронной теории привело к утверждению первой интерпретации (в обновленной форме, см. выше). При этом уравнения электромагнитного поля дополняются уравнениями механики электронов, определяющими движение электрона в заданном «внешнем» электрическом поле. При таких условиях электромагнитное поле может рассматриваться как посредник в процессе взаимодействия электронов, принципиально несущественный для характеристики этого взаимодействия и связанного с ним движения.

Однако, не исключена возможность того, что вторая интерпретация окажется в дальнейшем если не практически, то принципиально более правильной. Возможность эта связана с электромагнитной интерпретацией массы, то есть сведением ее к энергии электромагнитного поля, создаваемого соответствующей частицей. При таких условиях уравнения движения электрона могут быть выведены из дополнительного принципа, относящегося к электромагнитному полю и не содержащегося в уравнениях Максуэла-Лоренца (последние с точки зрения второй интерпретации служат лишь для определения величин ρ и, характеризующих состояние материи).

Этим дополнительным принципом является принцип сохранения электромагнитной энергии и связанный с ним принцип сохранения электромагнитного количества движения.

Понятие электромагнитной энергии как величины, распределенной в электромагнитном поле, получается, исходя из рассмотрения работы электромагнитных сил. Если не разделять электромагнитное поле, связанное с движением электрона, на «внешнее» (происходящее от других электронов) и собственное, то работа сил, действующих в объеме V за единицу времени может быть определена интегралом

обозначает скалярное произведение векторов (напомним, что магнитные силы, будучи перпендикулярны к направлению движения, не совершают работы). Если в произведении заменить вектор его выражением через то после простых преобразований интеграл, определяющий работу, приводится к виду

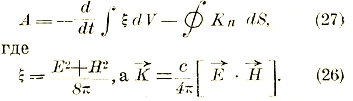
S обозначает замкнутую поверхность, ограничивающую есть так называемое внешнее или векторное произведение векторов то есть вектор, перпендикулярный к ним обоим и равный площади параллелограмма, на них построенного.

Отбрасывая второй интеграл в (26) мы, естественно, должны интерпретировать интеграл

как энергию, заключенную в объеме V — так как за счет этой величины получается работа, производимая действующими в V силами. Полагая А = 0 и принимая во внимание второй член в правой части, мы оказываемся вынужденными рассматривать его как поток энергии, вытекающей в единицу времени через поверхность S. Введением этого потока обеспечивается справедливость принципа сохранения энергии при А = 0. Если в объеме V содержится электрон, то равенство А = 0 возможно лишь при том условии, что силы, действующие на электрон извне, уравновешиваются силами взаимодействия его собственных элементов. Но, как мы видим выше, именно к этому условию и сводится электромагнитная теория массы.

Преобразуя поверхностный интеграл

по формуле Гаусса в объемный

и полагая А = 0, мы можем выразить принцип сохранения энергии в виде дифференциального уравнения:

аналогичного уравнению (18), выражающему закон сохранения электричества.

Необходимо, однако, отметить, что уравнение (28) не может быть применено к отдельным точкам электрона, так как силы, действующие на отдельные элементы его, отнюдь не находятся в равновесии, которое может осуществляться лишь в среднем для всего электрона.

Если в предыдущих рассуждениях вместо работы сил ввести в рассмотрение импульс их за единицу времени, то есть самые силы, то вместо уравнения энергии (26) получается уравнение того же вида, где скаляр ξ в объемном интеграле заменен вектором

а вектор в поверхностном интеграле - тензором напряжений (с обратным знаком), который уже был введен нами в конце I главы. Соответственно этому вектор может быть интерпретирован как объемная плотность электромагнитного количества движения, а тензор — — как плотность потока количества движения.

В механике количество движения определяется как произведение массы на скорость. Аналогичным образом вектор можно рассматривать как произведение плотности массы электромагнитного поля на скорость его распространения. Точно так же вектор (поток энергии, вектор Пойнтинга) можно определить как произведение последней на плотность энергии. Таким образом, оказывается, что с энергией электромагнитного поля неразрывно связана его масса, равная энергии, деленной на квадрат скорости света.

В заключение нам остается сказать несколько слов об уравнениях электромагнитного поля в материальных телах (средах). Здесь вместо истинного поля рассматривают усредненное или сглаженное поле, соответствующее представлению о теле не как о системе дискретных частиц, а как о континууме.

При этом плотности ρ и разделяются на две части, зависящие от свободных и от связанных зарядов. Последние определяются через векторы электрической поляризации и намагничения по формулам

Что касается первых, то плотность тока определяется формулой

где σ — коэффициент электропроводности (в электромагнитных единицах), а ρ считается равной нулю (в проводниках электрический заряд распределяется на поверхности). Таким образом, уравнения Максуэла-Лоренца (10) и (14) принимают вид

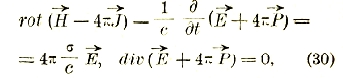
между тем как уравнения (11) и (15) остаются без изменения.

Далее полагают (ε — диэлектрическая постоянная), разность обозначают через, а  пишут в виде

 (μ — магнитная проницаемость). В случае диэлектриков, совершенно лишенных проводимости (σ = 0), мы получаем, таким образом, систему уравнений

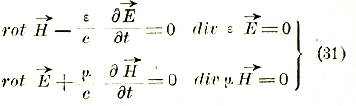
В простейшем случае однородной среды (ε и μ постоянные) отсюда получается для уравнение вида

выражающее тот факт, что усредненное поле в подобной среде распространяется так же, как истинное поле в пустоте, но не со скоростью с, а со скоростью

Отсюда, между прочим, следует, что показатель преломления однородной среды по отношению к пустоте равен

 или практически

(за исключением медленных колебаний в ферромагнитных телах).

Литература: Я. И. Френкель, «Курс электродинамики»; Абрагам, «Теория электричества»; Иг. Тамм, «Теория электричества», т. I; О. Хвольсон, «Курс физики» (т. IV, V).

Я. Френкель.