Электротехника. I. Теоретические основы электротехники

Электротехника. Современная электротехника, развившаяся на основе чисто физического учения об электричестве (см. LII, 9 сл.) и магнетизме (см. XXVII, прил., 579' сл.), представляет собой в настоящее время обширную область прикладного знания. Поэтому оказалось необходимым выделить два больших основных раздела: электротехника слабых токов и электротехника сильных токов. Хотя строгой границы между ними провести невозможно, все же обычно к первому относят технику проволочной и беспроволочной связи: телеграфию (см. XLI, ч. 7, 219 сл.), телефонию (см. XLI, ч. 7, 262 сл.) и радио (см. XXXV, 362 сл.), а также сигнализацию и блокировку. Электротехника  сильных токов также распадается на ряд отделов. Здесь, прежде всего, нужно выделить общие отделы, подводящие базу под все области применения электричества и магнетизма в технике: теоретические основы электротехники, изучающие техническую интерпретацию физических законов и являющиеся как бы мостом между физикой и техникой; технику электрических измерений, включающую в себя приборы и способы измерений и учета как электрической энергии, так и факторов, ее создающих (тока, напряжения и т. д.); электроматериаловедение, рассматривающее и изучающее свойства материалов, применяемых в электротехнике — свойства, иногда резко отличающиеся от свойств обычных материалов; отдел электрических машин, рассматривающий аппараты для получения (генерирования), преобразования электрической энергии и превращения ее в механическую. На основе этих четырех отделов развивается и продолжает бурно расти прикладная электротехника, включающая в себя отделы: электростанции и сети, электромоторный привод, электротехника в промышленности (с целым рядом разветвлений), электротехника в сельском хозяйстве, электротехника в быту, электрический транспорт, электрическое освещение и т. д.

I. Теоретические основы электротехники. Теоретические основы электротехники содержат в себе изложение методов количественного и качественного анализа электромагнитных явлений с точки зрения их технического использования. Теоретические основы электротехники пользуются трудами основоположников современного физического учения об электричестве (см. электричество и магнетизм). Однако, здесь имеется ряд собственных основных вопросов, разработанных учеными и инженерами: Т. Г. Блекслей («Papers on alternating currents of electricity», 1880), Ч. Штейнметц (1893), А. Кеннелли, Г. Феррарис, Хевисайд, Н. Тесла, М. Доливо-Добровольский, Лакур, Брагштад, Фортескью и др. Сюда относятся: метод векторных диаграмм, символический метод, метод инверсных диаграмм, метод суперпозиции, теория трехфазного тока, применение рядов Фурье, теория неустановившихся явлений и др.

Основные понятия: электрический ток и электрическое напряжение. Согласно воззрениям современной электронной теории, электрический ток представляет собой движение атомов электричества (электронов) с отрицательным зарядом, равным  ≈ 0,16·10^-20 кулона. Электроны имеют значительно меньшую массу, чем атомное ядро, и от каждого атома могут быть отщеплены один или несколько электронов. После такого отщепления атом (или группа атомов — молекула), оставаясь заряженным положительно, превращается в положительный ион (атом или молекула ионизируется); наоборот, при увеличении числа электронов получается отрицательная ионизация атома. В нейтральном состоянии число электронов равно числу элементарных положительно заряженных элементов ядра атома (протонов).

Указанный процесс ионизации может сопровождаться и такими явлениями когда целая группировка молекул, образующая молекулу какого-либо сложного вещества, расщепляется (диссоциируется) на части с избытком и недостатком электронов. Такой случай мы имеем главным образом в электролитах (проводящих жидкостях). Установлено, что при этом недостаток электронов получается у молекул металлов и водорода, которые и дают положительно заряженные ионы, называемые исторически ошибочно катионами, так как отлагаются на отрицательном полюсе (катоде) в электролитической ванне (рис. 1). Отрицательно заряженные ионы с избытком электронов называются анионами (направляются к аноду).

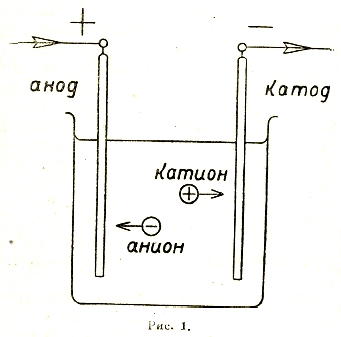
Рис. 1.

Принятое теперь нами направление электрического тока было взято именно из наблюдения над электролитическим выделением металлов. Как известно, применение электричества в промышленности началось с гальваностегии. Оказывается, что движение электронов и отрицательно заряженных ионов идет в направлении, обратном принятому нами направлению электрического тока.

В соответствии с описанным выше электрический ток может получаться лишь тогда, когда его цепь составлена из таких тел, в которых могут образоваться свободные (отщепленные) электроны или молекулярные ионы. Причем эта цепь должна быть замкнута, так как иначе в месте размыкания должны были бы непрерывно накопляться все большие и большие количества электронов или ионов, не соответствующие действующему в цепи источнику электрического напряжения (источнику энергии). В газах (и парах) указанная ионизация происходит под влиянием естественных и искусственных ионизаторов; сюда относятся: высокая температура, ультрафиолетовые и рентгеновские лучи, радиоактивные излучения, космические лучи. При высоком напряжении эта начальная стадия ионизации переходит в самоионизацию толчком, которая приводит к электрическому разряду в газах по следующим стадиям: тихий разряд искровой и, наконец, дуговой. В жидкостях явление ионизации (ее принято называть электролитической диссоциацией) происходит под влиянием диссоциирующих свойств растворителей. В твердых телах движения ионов не происходит, а могут двигаться лишь отщепленные (свободные) электроны. Поэтому различают ионную проводимость газов, электролитическую проводимость жидкостей (электролитов) и электронную проводимость металлов (проводников, электродов). Существуют тела, в которых не только нет движения ионов, но также и не могут получаться в заметном количестве свободные электроны. Такие тела почти не обладают проводимостью и называются изоляторами. Однако, в них под действием электрического поля происходит электрическая поляризация атомных и молекулярных систем, происходящая главным образом за счет смещения орбит движения электронов, и поэтому они все же не остаются электрически инертными и называются диэлектриками. Строго говоря, во всех телах оба эти явления — проводимость и поляризация — происходят одновременно, но только в разной степени.

Для того, чтобы ионы и свободные электроны двигались, недостаточно, однако, одного только их наличия, а необходимо, чтобы они находились под действием электрических сил. К настоящему времени подробно еще не выяснена природа действия этих сил. Можно считать установленным лишь то, что: во-1) это действие связано с электромагнитными свойствами мирового пространства  (или особой электромагнитной среды — мирового эфира в этом пространстве); во-2) это действие не распространяется мгновенно, а со скоростью порядка скорости света — 3 1010 см/сек., в зависимости от среды; и, наконец, в-3) что оно происходит от скопления положительных и отрицательных зарядов (недостаток или избыток электронов), причем это действие передается на любое расстояние. По последнему пункту говорят, что между данными областями среды (областями скоплений разноименных зарядов) — электрическими полюсами — действует электрическое напряжение. Причины возникновения таких полюсов разнообразны. В атмосфере, в условиях ионизированного воздуха такие скопления могут получиться на движущихся густых облаках (грозовые явления), на металлических остриях (атмосферные свечения). При прикосновении разных металлов непосредственно или через электролит получается контактное напряжение из-за явления электронного осмоса (гальванические элементы). При нагревании спаев разных металлов получаются электрические полюсы (термоэлементы). Наконец, самые мощные современные электротехнические источники напряжения образуют его под влиянием электромагнитной индукции.

Цепь постоянного (прямого) тока. Под постоянным током разумеется ток неизменного направления и неизменной силы. В тех случаях, когда хотят обобщить это понятие в смысле только одного неизменного направления, говорят о прямом токе. Прямой ток меняющейся силы называют еще иногда пульсирующим током.

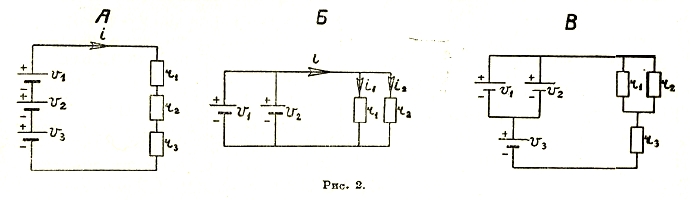
Рис. 2.

При постоянном токе легче установить основные законы электрического тока. Его цепь должна быть замкнута. В состав цепи входят один или несколько источников энергии, потребители энергии и соединительные проводники. Все эти элементы могут быть соединены последовательно, параллельно или смешанно (последовательно-параллельно; см. рис. 2).

Между результирующим напряжением v, действующим в цепи, и силой тока i имеется простая пропорциональная зависимость, установленная германским физиком Омом и носящая название закона Ома:

V=ri

Коэффициент пропорциональности r Ом назвал электрическим сопротивлением. Действительно, представляя закон Ома в другой форме:

I=v/r

мы видим, что чем больше r, тем меньше сила тока i. Этот простой и в то же время фундаментальный закон является  для электротехники в количественном отношении очень важным. Оказывается, что электрическое сопротивление каждого проводника зависит в свою очередь от его длины I, сечения q и материала:

r=ρl/q

Для металлических проводников I принято измерять в метрах, а q — в квадратных миллиметрах. Для жидкостей (электролитов) и то и другое — в сантиметрах и, соответственно, квадратных сантиметрах. Удельное сопротивление ρ найдено для различных веществ опытом.

Прежде всего, закон Ома позволяет установить единицы для измерения основных электротехнических величин: напряжения и силы тока. Согласно приказу ВСНХ СССР от 26/1.1925 г., по представлению Всесоюзного института мер и стандартов (ВИМС), обязательными для всего Союза ССР являются следующие основные единицы:

1. Международный ампер есть величина неизменяющегося электрического тока, который отлагает 0,00118 грамм серебра в секунду, проходя через водный раствор азотнокислого серебра. Ампер подразделяется на 1 000 миллиампер или 1 000 000 микроампер.

2. Международный Ом есть сопротивление, оказываемое неизменяющемуся электрическому току при температуре тающего льда ртутным столбом, имеющим повсюду одинаковое поперечное сечение, длину 106,3 см и массу в 14,4521 г, что соответствует сечению в 1 мм². Ом подразделяется на 1 000 000 микромов. 1 000 000 ом составляет один мегом.

Международный вольт есть электрическое напряжение, которое в проводнике, имеющем сопротивление в один Ом, вызывает ток в один ампер. Вольт подразделяется на 1 000 милливольт. 1 000 вольт составляет один киловольт. Нормальный элемент Вестона имеет напряжение, равное 1,0152 вольт.

Электрическое сопротивление зависит еще от температуры проводника по биноминальному закону:

r_t = r₀ (1 + αt),

где α —  т. н. температурный коэффициент.

Приводим значения для  ρ = rq/l в Ом = мм²/метр для некоторых проводников:

С помощью закона Ома можно весьма просто изучать явления лишь в чисто последовательных цепях (рис. 2А). В этом случае сопротивления отдельных проводников, являющихся элементами замкнутой цепи, просто складываются, причем в каждом таком отдельном сопротивлении происходит падение напряжения: е = іr.

В случае параллельного (рис. 2Б) и смешанного (рис. 2В) соединения или вообще в случае разветвленной цепи задачу о токораспределении можно решить, лишь пользуясь следующими двумя правилами Кирхгофа.

1- е правило: во всякой точке разветвления (и вообще во всякой точке) электрической цепи сумма токов притекающих равна сумме токов утекающих.

2- е правило: во всяком замкнутом контуре разветвленной цепи алгебраическая сумма действующих напряжений источников равна такой же сумме падений напряжений на отдельных участках этого контура.

Отсюда, например, вытекает, что в параллельных ветвях (1) и (2) (фиг. 2) токи будут обратно пропорциональны сопротивлениям. Действительно, по 2-му правилу: 0 = i₁r₁ — i₂r₂. А стало быть i₂r₂ = i₁r₁ или i₁/i₂=r₂/r₁. Для нескольких параллельных ветвей: i_n=1/r_n или i_nr_n = пост. Так как, согласно первого правила, I = i₁ + i₂, то эквивалентное сопротивление двух параллельных ветвей получится следующим образом: 1/R = 1/r₁ + 1/r₂ или R=r₁r₂/(r₁+r₂)

На основании указанных правил возможно задачу о токораспределении решить в любом случае. Для этого надо составить уравнения напряжений по контурам и уравнения токов по узловым точкам так, чтобы общее количество уравнений соответствовало числу неизвестных. Совместное решение этой системы уравнений дает нужные результаты.

Иногда удобно пользоваться методом суперпозиции (наложения) действующих напряжений (электродвижущих сил), вытекающим из принципа независимости действия электрических сил. По этому методу находят в отдельных ветвях те слагающие тока, которые получились бы, если бы по всей цепи действовал лишь один из группы источников напряжения, а остальные были бы представлены лишь своими внутренними сопротивлениями.

При решении задач о параллельных соединениях пользуются понятием в проводимости, как величине обратной сопротивлению: g=1/r

Проводимости параллельных ветвей просто складываются:

в то время как в последовательном соединении складываются сопротивления:

Единицей для измерения проводимостей служит МО — проводимость одного Ома.

Как будет установлено впоследствии, в разделе об электрическом поле, электрическая энергия может выражаться через произведение силы тока на напряжение и на время:

А = V·l·t.

Таким выражением энергии, дающим количество работы, нельзя, однако, полностью охарактеризовать энергетические возможности какого-либо устройства. Поэтому введено понятие о мощности, представляющей собой энергию в 1 сек.

Р=A/t=V·I

Единицей для измерения энергии (работы) мог бы служить джоуль, равный вольтамперсекунде и в то же время работе силы в 1/9,81 = 0,102 кг на протяжении одного м. Если принять во внимание, что по стандарту ОСТ 169 рекомендуемой в Союзе единицей силы является один стен (сокращенно — сн), равный силе, сообщающей массе в одну тонну ускорение в один м в сек.² и равный 102 кг силы, то джоуль может быть представлен как 0,001 снм (1 кдж  = 1 снм). Однако, в практической электротехника поступают иначе, а именно: пользуются единицей, установленной для измерения мощности — 1 ваттом. 1 ватт равен мощности какого-либо устройства, в котором преобразуется 1 джоуль энергии в сек. Отсюда энергия может измеряться в ваттсекундах или производных от этой единицы: гектоваттчасах, киловаттчасах, меговаттчасах (гвч, квч, мвч). Гаусс впервые показал, что можно построить систему взаимно-связанных единиц, названную им абсолютной. В этой системе за единицу работы принят эрг — работа 1 дины силы на протяжении 1 см. Оказалось далее, что 10⁷ эрг может быть принято равным вышеупомянутой единице — джоулю.

В одной лошадиной силе содержится 736 ватт или 736 джоулей/секунду, а в одном кгм — 9,81 джоулей.

Указанное выше выражение энергии может быть с помощью закона Ома преобразовано следующим образом: А = Vlt =  l²r   It = I²rt

В таком виде получается закон Джоуля-Ленца, найденный ими на опыте с получением тепла от электрического тока. Действительно, тепло выделяется во всех случаях, когда по проводнику течет электрический ток. Это приводит к необходимости рассчитывать провода на нагревание, причем основной величиной, определяющей этот нагрев, является т. н. плотность тока, т. е. число ампер, приходящееся на 1 кв. мм сечения провода. Выделяющееся тепло можно подсчитать еще и следующим образом:

Здесь j — плотность тока; ρ — удельное сопротивление: для меди 1/57, а в нагретом состоянии около 1/48; v — объем в см³.

Отсюда в медном проводе выделяется энергии в сек. в ваттах на 1 кг:

(8,9 — удельный вес меди). Это тепло отдается проводом в окружающую среду по уравнению:

I²rt =  ατot;

здесь α — коэффициент теплоотдачи; τ — превышение температуры проводника; о — поверхность охлаждения (для цилиндра пров. о=10·πdl см²; d — диаметр проволоки в мм). Следовательно:

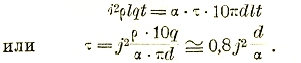
Как показывает опыт, для того, чтобы превышение температуры проводов не превосходило 15°С, необходимо, чтобы плотность тока не была больше величины порядка 2 А/мм². Естественно, что в нагревательных приборах эта плотность тока берется соответственно больше.

Провода должны быть рассчитаны также на падение напряжения е = lr. Обыкновенно это падение напряжения задается в процентах от полного напряжения сети (е%) и равно 3—5 до 10 %.

Тогда:

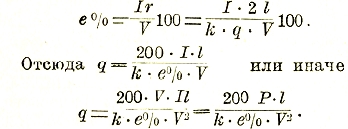
Электрическое поле. Если цепь электрического тока будет разомкнута, оканчиваясь, например, двумя параллельными металлическими пластинками (рис. 3), то под действием электрического напряжения, действующего в этой цепи, между указанными пластинками (а также и вообще во всем окружающем эту цепь пространстве) установится электрическое поле, т. е. в пространстве между ними будут действовать электрические силы. Это обнаруживается при помощи испытательного заряженного тела, которое получает стремление двигаться в этом поле. Электрическое поле получится между пластинками также и тогда, когда они будут совсем отсоединены от источника и на них останутся разноименные заряды. Поле можно возбудить и постепенным накоплением зарядов на его границах путем механического переноса их от полюсов источника или использования явления электростатической индукции. На этом принципе основано действие электростатических машин. Это дает право считать, что электрическое поле вполне обусловливается электрическими зарядами, взятыми даже отдельно. Электрическое поле приобретает большое практическое значение в двух случаях: при высоких напряжениях и при высоких частотах изменения тока (радиотехника).

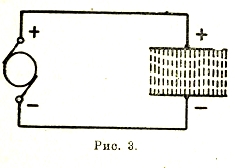
Рис. 3.

Основным законом, на котором построены все количественные соотношения в электрическом поле, является опытный закон французского физика Кулона, обобщаемый затем теоремой Гаусса и, наконец, понятием о потенциале поля. Согласно этому закону, два заряженных тела очень малых размеров по сравнению с расстоянием между ними (два точечных заряда), помещенные в однородную среду, испытывают взаимодействие с силой F, пропорциональной самим зарядам q₁ и q₂ и обратно пропорциональной квадрату расстояния r:

F = q₁q₂/εr²

где r — т. н. диэлектрический коэффициент среды. Этот закон позволяет в нужном случае найти основную величину, характеризующую электрическое поле в какой-либо точке, т. н. силу поля или  иначе, его напряженность Э.

Действительно, давая определение напряженности поля в данной точке, как силе, которую испытывает положительный единичный испытательный заряд, помещенный в эту точку поля, мы будем в состоянии в любом случае рассмотреть источник этого поля с точки зрения элементарных точечных зарядов и составить сумму всех элементарных действий по какому-либо направлению. Так что:

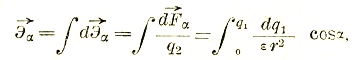
где  α — угол между каждой элементарной силой и выбранным направлением. Так, например, можно найти, что напряженность поля очень длинной равномерно заряженной прямолинейной оси в точках, отстоящих от этой оси на расстояние r в направлении, перпендикулярном к ней, будет равна

Э = 2q/εr

где q — плотность заряда оси на 1 погонный см. Естественно, что при этом надо условиться о единицах для измерения. Как будет подробнее показано ниже, для Э напряженность удобнее измерять в единицах некоторой удельной работы в вольт/см (вольт/см = вольт·кулон/см·кулон).

Тогда напряженность поля одного точечного заряда выразится так:

Иногда пользуются более простыми приемами нахождения напряженности поля. К таковым относится условное представление о силовых линиях, вдоль которых действуют силы поля и которые являются, таким образом, траекториями движения в поле испытательных зарядов без инерции. Если принять, что каждой такой силовой линии соответствует единица силы поля, то густота линий на 1 см² может характеризовать напряженность поля в направлении перпендикулярном к этой элементарной плоской площадке в 1 см², проходящей через данную точку. Пользуясь таким представлением, можно во многих случаях изобразить приближенный спектр поля и оценить, например, в каком месте поля напряженность будет наибольшей   (рис. 4). При вычерчивании таких спектров надо только иметь ввиду, что силовые линии заканчиваются у металлических поверхностей перпендикулярно к ним, так как иначе получится тангенциальная составляющая силы поля, при которой неизбежно движение зарядов вдоль этих поверхностей.

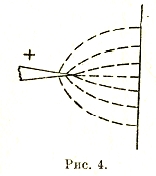
Рис. 4.

В соответствии с представлением о силовых линиях установлена теорема Гаусса, по которой общее число единичных силовых линий (единичных силовых трубок), проходящих через любую замкнутую поверхность, или поток вектора напряженности электрического поля, приходящийся на эту поверхность, равен:

где ∑q — сумма зарядов, заключенных внутри поверхности. Действительно, для частного случая шаровой поверхности радиуса r с зарядом q в центре

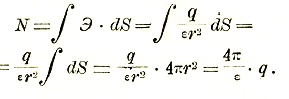
Теорема Гаусса позволяет очень просто находить напряженность поля в ряде случаев. Так, например, для поля заряженной неограниченной металлической плоскости напряженность поля получится, если подсчитать поток чрез две плоскости, охватывающие данную:

здесь  σ — плотность заряда на 1 см². Отсюда мы видим, что напряженность поля пластины является одинаковой для всех точек, независимо от расстояния. Такое поле называется равномерным (рис. 3).

Для цилиндрического поля (рис. 5.) подобным же образом

Легко также доказать, что внутри заряженного полого металлического шара напряженность поля равна нулю (как говорят — поля нет). Действительно, если рассмотреть какую-либо внутреннюю шаровую поверхность, то нетрудно видеть, что сколько линий входит чрез нее внутрь, столько и должно выходить, т. е. результирующий поток равен нулю. Отсюда же вытекает, что для электрического поля двух разноименно заряженных параллельных пластин напряженность поля между пластинами равна 4πσ/ε, а вне их равна нулю (рис. 6).

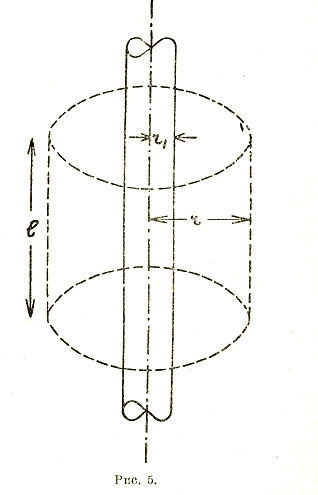
Рис. 5.

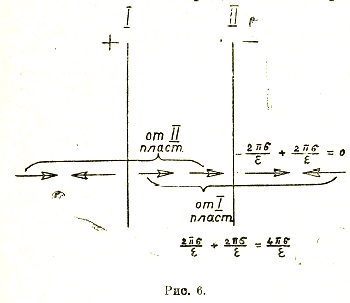
Рис. 6.

Наиболее удобным и в то же время более обобщенным определением напряженности является определение через изменение (падение) потенциала поля на 1 погонный см по выбранному направлению. Действительно, так как напряженность поля есть сила, то выражение ∫Эdr должно представлять собой работу сил поля при перемещении единичного заряда из одной точки в другую. С другой стороны, в теоретической физике установлено, что поле неподвижных электрических зарядов потенциально, т.  е. оно обладает в каждой точке скалярной величиной (потенциалом), которая вполне определяется лишь положением этой точки и пограничными условиями поля и не зависит ни от времени, ни тем более от какого-либо направления отсчета. Сопоставление этих двух положений позволяет, оказывается, принять, что напряженность поля равна градиенту потенциальной функции, взятому с обратным знаком: -

Э = -dV/dr = -grad V.

Это обстоятельство тем более важно, что разность потенциалов по границам поля равна электрическому напряжению между этими границами, которое очень легко измерить приборами. Установив, например, что (см. выше) напряженность поля между пластинами есть величина одинаковая и равная 4πσ для всех точек, мы вправе прямо написать, что

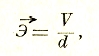
где V — напряжение между пластинами, а d — расстояние между ними в см. Отсюда возникает и единица для измерения напряженности, а именно вольт/см. Чрез заряд на пластинах напряженность выражается:

Для поля между двумя цилиндрами радиусов r₂ и r₁, выражение напряженности поля чрез напряжение между границами получится, если воспользоваться уравнением:

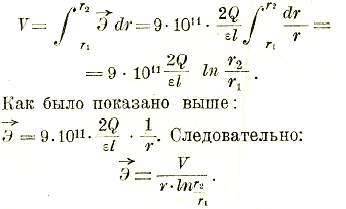
Подобным же образом для шарового поля:

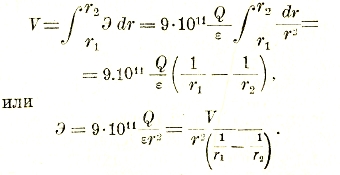
Для поля между двумя проводами напряженность в точках на линии, соединяющей оси проводов, равна

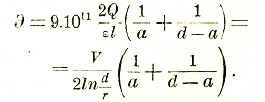
Здесь: d — расстояние между проводами, r — радиус провода и а — расстояние какой-либо точки до оси одного из проводов. Для исследования поля между проводом и землей служит особый прием т. н. зеркального изображения, рассматриваемого провода в земле (рис. 7). Поле получается в своей верхней половине совершенно идентичным с действительным, если напряжение между рассматриваемым проводом и фиктивным взять в два раза больше, чем по отношению к земле.

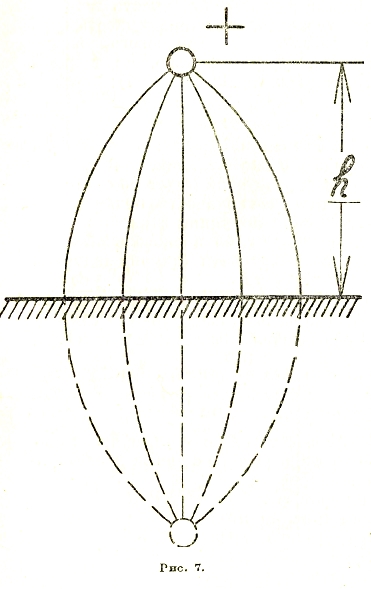
Рис. 7

Предыдущее выражение представится в следующем виде:

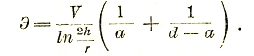
При помощи описанных выше соотношений можно найти электрическую емкость конденсаторов, т. е. отношение количества электрического заряда на его обкладках к напряжению:

C=Q/V.

Если измерять Q в кулонах, а V в вольтах, то емкость выразится в единицах емкости – фарадах. Так как эта единица очень велика для практических целей, то употребляют от нее производные, а именно  μF — микрофарад (10^-6 фарад) и μμF — микромикрофарад (10^-12 фар.). Встречается также 1 см емкости, равный 1/9·10^-11 фарады (1  μμF = 0,9 см).

Так, емкость шарового конденсатора оказывается равна:

Конденсаторы могут быть соединены последовательно и параллельно. При этом первое соединение отличается, во-1) , тем, что заряд остается неизменным на всех конденсаторах — Q = const и, во-2), тем, что внешнее напряжение равно сумме напряжений на отдельных конденсаторах. Отсюда может быть найдена результирующая емкость всего соединения. Действительно, так как

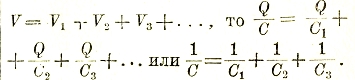
При параллельном соединении емкости просто суммируются: С = С₁ + С₂ + С₃ +…

При решении электротехнических вопросов помимо задачи о емкости приходится иметь дело также и с расчетом диэлектриков. Как уже было указано, диэлектрики под влиянием электрического поля поляризуются. Влияние такой диэлектрической поляризации обнаруживается простейшим образом тем, что емкость какого-либо конденсатора увеличивается при введении в него диэлектрика. Если конденсатор с диэлектриком зарядить и, отсоединив предварительно от источника, вывести из него диэлектрик, то, как показывает опыт, напряжение на его пластинах увеличится. Последний опыт показывает, что при том же электрическом смещении результирующая напряженность поля при наличии диэлектрика снижается. Исследования показывают, что количественно указанные изменения происходят в отношении диэлектрического коэффициента ε, что и было уже нами учтено. Из только что описанного опыта с изменением емкости вытекает, между прочим, способ опытного нахождения диэлектрического коэффициента какого-либо диэлектрика.

Явление почти только одной поляризации диэлектриков (изоляторов) при очень незначительном токе объемной и поверхностной проводимости происходит, однако, только до определенного предела напряженности поля. После этого предела возникают новые явления, которые приводят к т. н. электрическому пробою изоляторов. Та напряженность поля, при которой происходит пробой диэлектрика в равномерном электрическом поле, носит название электрической крепости диэлектрика.

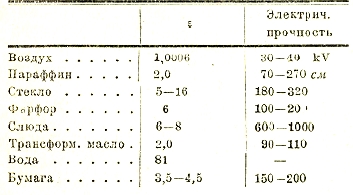
Приводим таблицу опытных данных относительно диэлектрических коэффициентов и электрической прочности.

В связи с расчетами на электрическую прочность необходимо бывает исследовать электрическое поле в каком-либо устройстве с точки зрения определения места с максимальной напряженностью поля. В случае цилиндрического поля этим местом является поверхность внутреннего цилиндра, и максимальная напряженность равна:

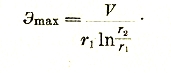
Для поля между двумя проводам место наибольшей напряженности находится у поверхности проводов на линии, соединяющей их оси, причем

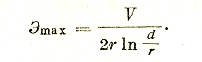
В случае сложного диэлектрика необходимо бывает также учесть и то обстоятельство, что напряженность поля зависит от диэлектрического коэффициента. Действительно, из теоремы Гаусса (см. LII, 42 сл. и 237):

Тогда, имея ввиду, что свободным зарядам q на металлической поверхности границ поля будет соответствовать такое же количество поляризованных в силу индукции зарядов в окружающей среде по произвольной замкнутой поверхности (линии индукции неразрывны), следует принять dq/dS  за электрическое смещение на 1 см², которое обычно обозначается буквой D, так что Э = 4πD/ε   или, в практических единицах, Э = 9·10¹¹(4πD/ε).

В соответствии с этим, например, в плоском конденсаторе с двумя диэлектриками произойдет перераспределение (рис. 8) напряженности: Э₁:Э₂ = ε₁:ε₂ т. е. в диэлектрике с меньшим  ε напряженность поля будет больше. Поэтому при изготовлении изоляции стараются удалить воздушные прослойки и пузыри.

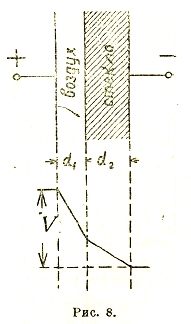
Рис. 8

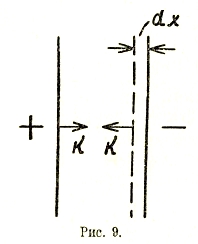
Рис. 9

В заключение главы об электрическом поле рассмотрим вопрос об его энергии. Для этого проследим процесс образования поля. Очевидно, что при этом должно иметь место накопление зарядов на границах поля и в связи с этим повышение напряжения. Тогда в каждой промежуточной стадии образования поля должна затрачиваться элементарная энергия:

dA=VdQ= VCdV.

Отсюда полное (конечное) количество энергии

А = CV²/2 = QV/2 джоулей.

Если отнести эту энергию к 1 см³, то получим:

A₁ = QV/2v = QV/2Sd = DЭ/2 джоулей/см³

Здесь v — объем, заключенный между границами поля; S - поверхность пластин-границ поля, а d — расстояние между ними. Это выражение позволяет определить силу взаимодействия, например, между пластинами плоского конденсатора (рис. 9). Дадим одной из пластин элементарное перемещение dx, для этого достаточно будет совершить механической работы: Kdx. Одновременно с этим энергия электрического поля изменится на: DЭ/2 Sdx.

По закону сохранения энергии:

K dx = DЭ/2 Sdx.

или

K = DЭ/2 S = QV/2d дин.

Магнитное поле. При движении электрических зарядов в форме ли электрического тока в замкнутой цепи из проводников, в форме ли изменения электрического смещения в диэлектриках или, наконец, в форме движущегося заряженного тела, в окружающем пространстве возникает магнитное поле, т. е. вокруг обнаруживаются магнитные явления, например, в виде взаимодействия между токами, действия тока на магнитную стрелку.

Исследование магнитного поля ведется примерно по той же схеме, как и в случае электрического поля. Основным понятием служит опять напряженность поля, как сила, действующая на единичный элемент тока, помещенный в данную точку.

Основным законом, на котором построены вычисления напряженности магнитного поля, является закон Био-Савара, в более обобщенном виде переходящий в первое уравнение Максвелла. Согласно этому закону, для того чтобы найти напряженность поля в какой-либо точке, надо разбить цепь тока на элементы длиной dl (рис. 10) и отыскать выражение вида:

где: r — расстояние каждого такого элемента до данной точки,  β — угол между направлениями r и dl, а k — коэффициент пропорциональности, зависящий от выбора единиц. Если, как это принято, измерять H в эрстедтах, силу тока I в амперах, а dl и r в см, то k = 0,1. Так, для поля тока в прямолинейном проводнике очень большой длины получается напряженность:

H = 0,2I/r₀

где r₀ — расстояние данной точки от провода. Направление силы поля находится по правилу правого винта. Для кругового тока напряженность поля в центре:

H = 0,2πl/r

где r — радиус круга тока.

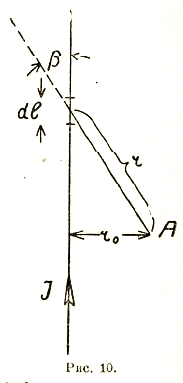
Рис. 10.

Максвелл дал уравнение (1-е уравнение Максвелла), согласно которому интеграл напряженности магнитного поля по замкнутому контуру (рис. 11) равен току, охватываемому этим контуром:

где dl — элемент длины контура (не смешивать с dl в законе Био-Савара).

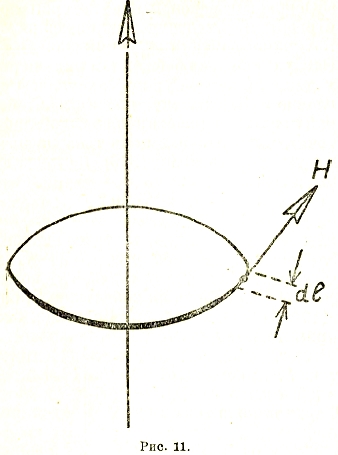
Рис. 11.

Легко видеть, что отсюда H = dI/d т. е. напряженность магнитного поля можно было бы рассматривать с точки зрения градиента магнитного потенциала подобно тому, как это имеет место в электрическом поле. Причем сила тока могла бы играть роль непосредственного фактора, устанавливающего потенциал магнитного поля. Однако, такое представление здесь осложняется тем обстоятельством, что магнитные силовые линии в противоположность электрическим являются замкнутыми, и потенциальная функция получается многозначной, т. е. неопределенной. Все же в пределах одного обхода магнитной линии напряженность поля можно, как оказывается, измерять в ампервитках/см. Для предыдущего случая прямолинейного проводника:

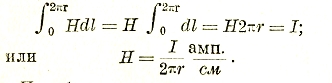
Подобно электрическому полю, напряженность магнитного поля может характеризоваться плотностью силовых магнитных линий. Так, установив, например, спектр магнитного поля достаточно длинного соленоида (рис. 12), можно сделать заключение, что внутри соленоида поле почти равномерное (H₁≈const) и, далее, что вне соленоида густота линий очень мала (H₁≈0). Отсюда вытекает важный практически результат, что в уравнении Максвелла, представленном в форме

вторым слагаемым можно пренебречь. Тогда при H₁≈const

H₁l = lW или H₁ = IW/l амп.витк./см., где I — длина соленоида.

Сравнивая выражение Н в эрстедтах и Н в амп./см, мы видим, что 1 А/см = 0,4π эрстед = 1,25 эрстед. Так, что число А/см: Н А/см = 0,8 Н эрстед. Общее число магнитных линий может представить собой поток вектора напряженности.

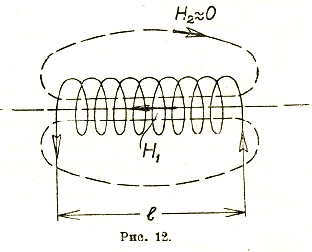
 Рис. 12.

Различные тела, помещенные в магнитное поле, испытывают в той или иной степени магнитную поляризацию. Согласно электронной теории, электроны, движущиеся вокруг атомных ядер, представляют собой систему круговых токов, или магнитных диполей, с осями, совпадающими с осями вращения; так как электроны обладают все же некоторой массой, то такие системы ведут, себя подобно волчкам.

Благодаря своему хаотическому расположению, эти круговые токи в нейтральном состоянии не проявляют никакого внешнего магнитного эффекта. Под влиянием же магнитного поля они начинают поворачиваться своими осями по направлению этого поля, принимая, таким образом, определенное ориентированное расположение. При этом, естественно, они продолжают находиться в состоянии хаотического теплового молекулярного движения. Как известно, при повороте оси волчка у него возникает еще добавочное прецессионное движение, которое в данном случае соответствует новому прецессионному круговому току, дающему магнитный эффект, противоположный внешнему полю. В зависимости от того, что превалирует — эффект ли основного движения электронов, усиливающий внешнее поле, или эффект прецессионного движения, ослабляющий поле, — различаются тела парамагнитные и диамагнитные. Первые втягиваются внешним полем, вторые, наоборот, выталкиваются им. Особо сильными парамагнитными свойствами обладают железо, никель, кобальт, а также марганец и сплавы. Явления, в них происходящие, носят название ферромагнетизма. В железе мы встречаемся, например, с явлением остаточной самоориентации молекулярных магнитных диполей, называемым остаточным магнетизмом. Весьма наглядной иллюстрацией этого эффекта служит опыт Юнга с магнитными стрелками. Железо играет очень видную роль в электротехнике, поэтому в дальнейшем мы рассмотрим магнитную цепь с железом.

Явления, возникающие при введении железа в соленоид с током, можно количественно рассмотреть двояким образом. Можно было бы считать, что магнитное поле усиливается под влиянием добавления к внешним ампервиткам соленоида ампервитков внутренних молекулярных токов, так что:

AW_рез = AW_сол + AW_внутр

Однако, исторически сложилось иное количественное представление. Подобно электрическому полю, где напряженности поля соответствует определенное электрическое смещение, устанавливают зависимость между напряженностью магнитного поля Н и плотностью магнитного потока индукции в железе В:

В = μН,

где μ — т. н. коэффициент магнитной проницаемости. Для воздуха и пустоты μ=1; для диамагнитных тел μ<1; для парамагнитных μ>1; для железа μ от 200 до 2000 и выше. Величина В называется просто магнитной индукцией и измеряется в гауссах, если Н выражено в эрстедтах. Ниже, в связи с электромагнитной индукцией, мы встретимся еще с другой единицей для измерения В.

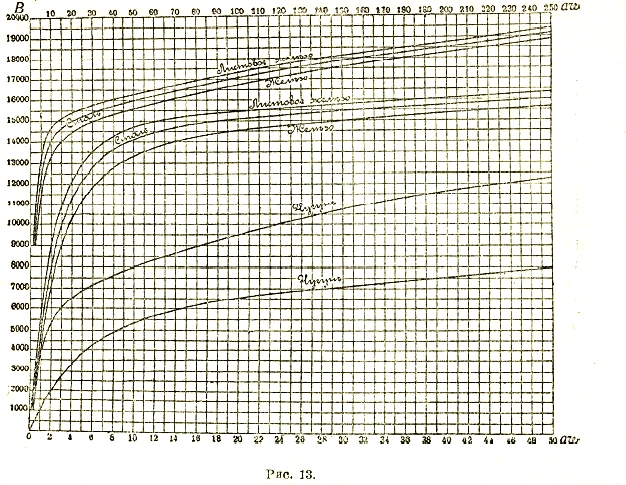
Рис. 13.

В соответствии с таким представлением опытным путем находят для различных сортов железа кривые В =  f(Н), т. н. кривые намагничивания (рис. 13). Как мы видим, кривые намагничивания, начиная с некоторого значения индукции (порядка 13 000 гаусс), загибаются по направлению к оси абсцисс: наступает, как говорят, магнитное насыщение железа.

Пользуясь приведенными соотношениями, можно вывести уравнение Гопкинсона для магнитной цепи, более известное под названием закона Ома для магнитной цепи. Действительно, если вначале представить себе такую цепь, составленную из замкнутого железного сердечника всюду одинакового сечения S см², причем для возбуждения магнитного потока пусть служит соленоид из W намотанных на этот сердечник витков с силой тока I ампер, то Ф = BQ = μНQ.

Но Н = 0,4πIW/l ампервитков/см, где l – длина  магнитной цепи. Тогда Ф = 0,4πμ.IW/l Q, или Ф = IW/(1/0,4π · l/μQ) = IW/R_μ

Выражение 1/0,4π · l/μQ носит название магнитного сопротивления, а IW — магнитного напряжения. Если теперь допустить в более общем случае, что магнитная цепь не однородна, а состоит из отдельных частей неодинакового сечения и изготовлена из неодинакового материала (включая и воздушный промежуток), то можно взять сумму магнитных сопротивлений этих последовательно соединенных частей.

Для параллельного разветвления магнитной цепи справедливы правила Кирхгофа. В соответствии с описанным может быть произведен расчет магнитной цепи, при котором ставится или задача о нахождении магнитного потока Ф по заданным размерам цепи и величине IW, или, наоборот, необходимое значение ампервитков (IW)  для возбуждения заданного магнитного формулировку этого закона, данную потока. Первая задача, однако, не может быть решена непосредственно, так как коэффициент проницаемости есть величина, зависящая от неизвестного в данном случае потока Ф. Поэтому решают всегда вторую задачу по схеме:

AW_общ = ∑aw_жl_ж + 0,8Вδ

Здесь: В — магнитная индукция в воздушном зазоре; δ — величина воздушного промежутка в см; aw_ж — напряженность поля в железе в ампервитках/см, находится из кривых намагничивания по плотности магнитного потока (В_ж = Ф/Q_ж); l_ж — длина железных участков магнитной цепи в см. Решив такую задачу для различных Ф, строят кривую Ф = f(IW) и после этого графически находят решение первой задачи.

Можно без преувеличения сказать, что все современное состояние электромагнетизма, в особенности сильных токов, обязано открытому в 1831 г. Фарадеем явлению электромагнитной индукции. Не касаясь очень поучительной самой по себе истории этого открытия, приведем формулировку этого закона, данную Максвеллом, как теоретически более удобную: в пространстве с изменяющимся магнитным полем во всяком замкнутом контуре действует электрическое напряжение, пропорциональное скорости изменения магнитного потока, охватываемого этим контуром (фиг. 14):

e = - dФ/dt

или в более общей форме: в пространстве, где действует переменное магнитное поле, одновременно возникает и вихревое электрическое поле, причем всякое изменение магнитного поля может быть представлено как поперечное перемещение уплотняющихся или разрежающихся силовых линий. Такое представление и было использовано Фарадеем, который наведенное в замкнутом образуемом каким-либо проводником контуре напряжение мыслил себе получающимся за счет скорости перерезывания этим проводником движущихся относительно него силовых линий: dN

e = - dN/dt

где N — число перерезанных линий.

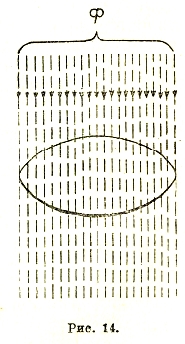
Рис. 14.

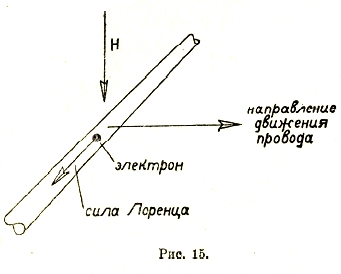
Рис. 15.

В связи с этими двумя формулировками происходил ряд недоразумений (встречающихся еще и в настоящее время), возникающих из-за предъявляемого иногда требования формальной универсальности их в применении к вихревому полю и к замкнутому вполне и не вполне контуру из проводников. Таково, например, положение вопроса об униполярной индукции, об опытах с так называемым изменяемым контуром, проблемы бесколлекторной машины постоянного тока. В ряде подобных случаев полезно иметь ввиду, что электроны, содержащиеся в веществе проводника или какой-либо другой среды, при всяком относительном поперечном движении их в магнитном поле испытывают силу Лоренца, увлекающую их в направлении, перпендикулярном к движению и к силе поля (рис. 15). Направление наведенного при электромагнитной индукции напряжения определяется проще всего по принципу Ленца, вытекающему из закона сохранения энергии: наведенное напряжение направлено всегда таким образом, что оно стремится вызвать электрический ток, препятствующий изменению потока (или индуктирующей причине вообще). Так, например, если на рис. 14 замкнутый виток находится под действием убывающего (спадающего) магнитного потока, то наведенное напряжение будет стремиться вызвать ток, поддерживающий прежнюю величину потока.

Выражение e = - dФ/dt позволяет  установить единицу для измерения магнитного потока, а именно — одна вольтсекунда.

В соответствии с этим и магнитная индукция, т.   е. плотность магнитного потока В = Ф/Q, может измеряться в вольтсекундах на 1 см². Исторически приняты, однако, единицы в 10⁸ раз мельче, а именно для В — гаусс = 10^-8 вольтсек./см² (см. выше) и для Ф — максуэл = 10^-8 вольтсек. Если принять во внимание, что под действием электромагнитной индукции могут находиться несколько последовательно соединенных витков, то тогда закон электромагнитной индукции примет следующую форму:

e = - WdФ/dt · 10^-8  вольт, где W — число витков. Это выражение является основным для электромашиностроения, так как позволяет вычислять напряжение в машинах и трансформаторах.

Наблюдения за явлением электромагнитной индукции показывают, что оно возникает также и тогда, когда по самому витку будет протекать от постороннего источника ток меняющейся силы. Действительно, тогда вокруг витка возникает собственное изменяющееся магнитное поле и поэтому в витке будет наводиться электрическое напряжение, как говорят, от самоиндукции. Это обстоятельство играет основную роль в цепях переменного тока. Для количественного учета явления самоиндукции вводится понятие об индуктивности (раньше наз. коэффициентом самоиндукции) какого-либо устройства:

e =  WdФ/di · 10^-8  или для воздуха L = WФ/i · 10^-8  

так что закон электромагнитной индукции принимает форму:

е = - L di/dt.

Как мы видим, индуктивность представляет собой число потокосцеплений (WФ), возникающее под влиянием прохождения тока силой в 1 ампер.

Индуктивность измеряется в единицах генри, причем 1 генри представляет собою индуктивность такой катушки, в которой при изменении тока на один ампер в секунду наводится 1 вольт напряжения.

Определим индуктивность катушки с W виткaми: L = WФ/i · 10^-8, но Ф = iW/R_μ, следовательно L =  W²/R_μ · 10^-8, где R_μ — магнитное сопротивление.

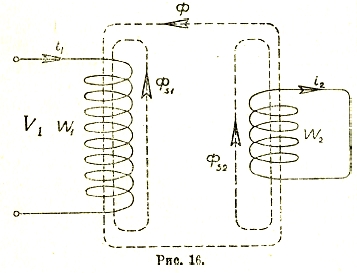
Рис. 16.

Индуктивность двухпроводной линии получается путем интегрирования магнитного потока между проводами при силе тока в 1 ампер:

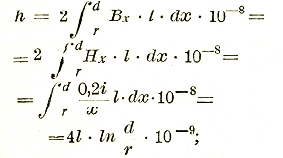
более точно с учетом потокосцеплений внутри сечения провода:

h = l(1+4ln d/r)·10^-9 генри.

Одновременно с самоиндукцией необходимо бывает также рассмотреть и явление взаимоиндукции между катушками (рис. 16). При изменении тока і₁ в первой катушке, во второй будет наводиться напряжение:

или, аналогично предыдущему:

М — наывается взаимоиндуктивностью (раньше коэффициентом взаимоиндукции). Наоборот, когда проходит ток і₂ во второй катушке, то в первой наводится напряжение

В общем техническом случае необходимо бывает учесть потоки рассеяния Ф_S1 и Ф_S2, которые сцепляются только с первой или со второй катушками. В этом случае уравнения балансов напряжений будут:

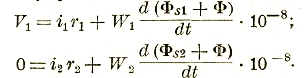
Во втором уравнении 0 вошел потому, что вторая катушка внешнего напряжения не имеет. Это уравнение физически правильней было бы написать в следующем виде:

Поток взаимоиндукции, передающий энергию из первичного контура во вторичный, наводится под действием двух токов i₁ и i₂, так что:

Потоки же рассеяния:

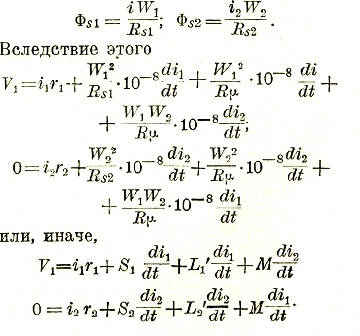
Коэффициенты  S₁ и S₂ суть индуктивности рассеяния; S₁ + L₁’ = L₁ и S₂ + L₁’ = L₂ наз. полными индуктивностями катушек. Очевидно, что:

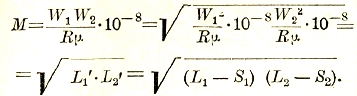
Магнитное поле содержит в себе определенное количество энергии, которое можно подсчитать, исходя из следующих соображений. На основании понятия об индуктивности очевидно, что всякое изменение тока в катушке и, следовательно, связанное с этим изменение магнитного потока, соответствует импульсу напряжения:

edt = — Ldi.

Если помножить обе части этого уравнения на силу тока i и, не обращая внимания на знак, взять интеграл:

то мы получим энергию магнитного поля, сцепленного с данной катушкой:

А = Li²/2 джоулей; при одном витке L=Ф/i · 10^-8 , так что A = Фi/2 · 10^-8 джоулей или А = Фi/2  абс. ед.

Рис. 17.

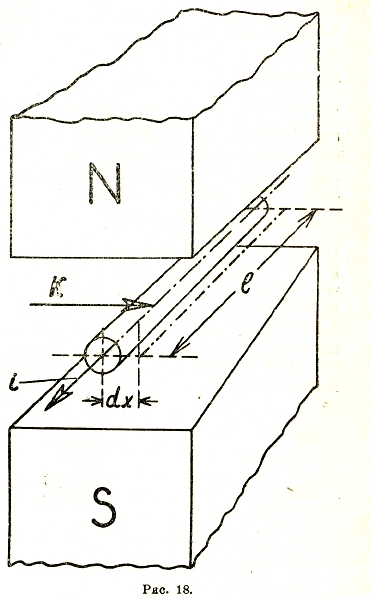
Рис. 18.

Энергия, отнесенная к 1 см³ объема, будет равна:

A₁ = Фi/2Ql = BH/2 или BH/8π

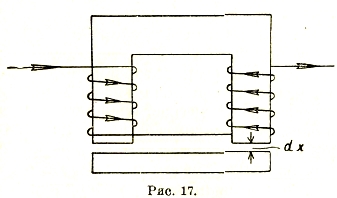
если все выразить в абсолютных единицах. Это выражение энергии позволяет решать задачи о силах, действующих в магнитном поле. Например, подъемная сила магнита, изображенного на рис. 17, будет найдена, если подсчитать энергию в пространстве Q·dx, где Q — поверхность соприкосновения якоря с магнитами:

K·dx = BH/8π · Q · dx

Отсюда K  = BHQ/8π дин. Для воздуха В = Н. Так что в кг

K = B²Q/9,81·8π · 10^-5 кг.

Силу, действующую на провод с током i, помещенный в магнитное поле с напряженностью Н, легче всего найти из следующих энергетических рассуждений (рис. 18). Дадим проводу перемещение dx. Тогда будет совершена механическая работа:

Kdx.

С другой стороны, при движении в проводе возникнет напряжение:

e = - dФ/dt = - dФ/dx · dx/dt = - Bx·l·v

где v – скорость движения. Это выражение само по себе является важным в теории электрических машин. Отвлекаясь от знака, мы получим:

е = B·l·v абсолютных единиц

е = B·l·v·10^-8 вольт.

По закону сохранения энергии:

К·dx = е·i·dt. Отсюда: К = B·l·I дин. Для воздуха В = Н, так что К = 0,1·Н·і·l дин (здесь і в амперах). Впервые это выражение было выведено Био и Саваром. Переводя в практические единицы, получим:

K = Hil/9,81 · 10^-6 кг.

Усилие между параллельными проводами можно найти, принимая, что один провод находится в магнитном поле другого:

подобное же выражение можно было бы вывести и исходя из изменения энергии магнитного поля между проводами при элементарном перемещении их:

K·dx = d(Li²/2).

В случае непараллельных проводов в выражение для К надо ввести в качестве множителя cos α, где α – угол  между проводами.

Указанное выше выражение энергии магнитного поля на 1 см² позволяет найти энергию, потерянную при намагничивании железа. Действительно:

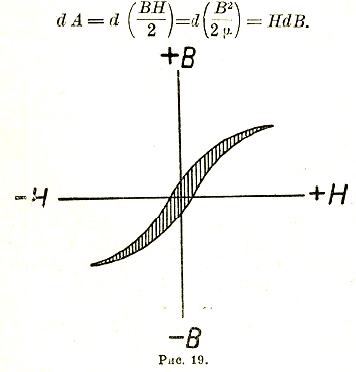
Как уже было указано, согласно опытам намагничивание железа идет по т. н. петлям гистерезиса (рис. 19). Причем за каждый цикл перемагничивания в железе остается энергии:

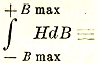 заштрихованной на рисунке площади.

Исследования Штейнметца и Рихтера показывают, что потери на гистерезис равны:

А  = h·f·В^γ·V джоулей.

Здесь: h — коэффициент, зависящий от сорта железа; f — число периодов перемагничивания; γ — по Штейнметцу = 1,6, по Рихтеру = 2; V — объем железа в см³ или дм³.

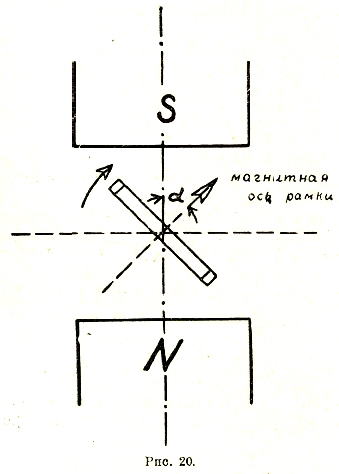
Рис. 20

Синусоидальный однофазный переменный ток. В основу рассмотрения процесса получения такого тока кладется теоретический генератор переменного тока. Этот генератор представляет собой рамку из нескольких витков, вращающуюся в равномерном магнитном поле с постоянной угловой скоростью  ω. Как видно из рис. 20, поток, охватываемый этой рамкой, меняется по закону косинуса:

Ф_t = Ф_max·cos α = Ф_max·cos ωt

В силу этого в рамке возникает напряжение электромагнитной индукции:

е = — w·dФ/dt·10^-8 =  ω·w·Ф_max sin ωt

т. е. тоже синусоидальной формы, причем максимальное значение E_max = ω·w·Ф_max  получается в тот момент, когда Ф = 0, и наоборот. Как говорят, между изменением магнитного потока и наведенным напряжением имеется сдвиг фаз (рис. 21).

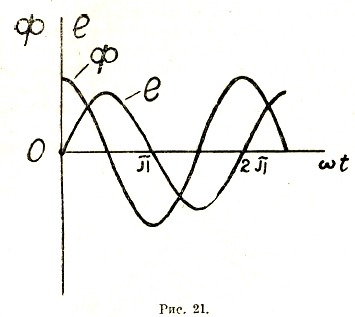
Рис. 21

Так как синусоидальный закон изменения напряжения и силы тока является, как будет показано в дальнейшем, наиболее благоприятным в цепях переменного тока, то в электротехнике предъявляют к генераторам переменного тока требование, чтобы они давали практически синусоидальное напряжение. Причем в электротехнических нормах под практической синусоидой разумеется такая кривая, ординаты коей не отличаются более, чем на ± 5% от ординат эквивалентной теоретической синусоиды.

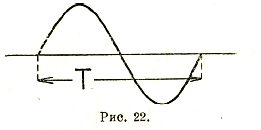
Рис. 22.

Основными понятиями, связанными с переменным током, служат: 1) период (рис. 22), измеряющийся в сек.; обозначается через Т; 2) частота переменного тока, или число периодов (число циклов) в 1 сек.; обозначается буквой f. Нормальной частотой в технике сильных токов является в СССР и в Европе 50 пер./сек.;  в Америке - 60 пер./сек.; один пер./сек. в Германии называют герцем. В технике высокой частоты (радиотехнике) частота измеряется сотнями и тысячами килоциклов в 1 сек. (килогерц). Постоянный ток есть ток, частота которого f=0, а период Т =  ∞. Очевидно, по самому взаимно обратному смыслу f и Т (число периодов в 1 сек. и число сек. в 1 периоде) f = 1/Т; 3) иногда встречается еще термин — число перемен: f’ = 2f (в 50 - периодном токе — 100 перемен в 1 сек.); 4) различают также угловую частоту ω = 2πf, т. е. частоту, выраженную в радианах в 1 сек.

Рассмотрение вопроса об измерении синусоидальных напряжений и сил тока приводит к тому заключению, что приборы, дающие всегда некоторое среднее значение измеряемой быстро меняющейся величины, в состоянии дать показание отличное от нуля только в том случае, если они работают по принципу квадратичных измерений (тепловые, электродинамические, электромагнитные, но никак не с постоянными магнитами). Поэтому вводится понятие о среднем квадратичном значении переменного тока и напряжения:

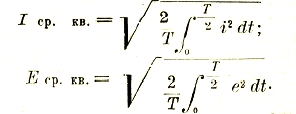
Для синусоиды это значение в √2 раз меньше максимального:

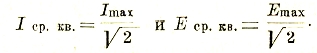
В дальнейшем будет показано, что от этих значений зависит также мощность переменного тока, что дало повод называть их эффективными значениями.

В теории машин и трансформаторов, как оказывается, все же играет роль также и среднее арифметическое значение напряжения за полпериода:  

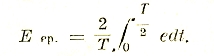
которое для синусоиды в π/2 раз меньше максимального:

Е ср. = 2/π Е_max.

Отношение эффективного (ср. квадр.) значения к среднему называется коэффициентом формы кривой k. Для синусоиды

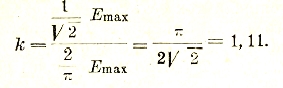
Теория переменного тока получается проще и нагляднее лишь при использовании метода символических векторов. Любое количество синусоидальных токов и напряжений, очень сложно взаимно распределенных по величине и фазе в цепи переменного тока, получает относительно простое изображение при помощи т. н. векторных диаграмм. В самом деле, пусть длина ОА некоего вращающегося вектора (рис. 23) представляет собой амплитуду переменного тока и пусть угловая скорость его вращения равно угловой частоте  ω этого тока. Тогда проекции ОВ вращающегося вектора на вертикальное направление Оу будут равны мгновенным значениям тока:

Для другого вектора ОС, опережающего первый на угол как  ψ, будем иметь:

Таким образом, оба вектора ОА и ОС могут быть рассматриваемы как символы двух переменных токов одинаковой частоты с амплитудами І_m1 и І_m2 и со сдвигом фаз ψ. Вращение этих векторов в электротехнике принято против часовой стрелки (в сторону положительного отсчета углов, принятого в аналитической геометрии). Вместо того, чтобы рассматривать вращение векторов, можно вообразить, что они неподвижны, а вращается в обратную сторону ось проекций, которая тогда называется линией времени. Однако, более удобным и распространенным является первое представление. Практически целесообразно при этом брать длины векторов равными в некотором масштабе не амплитуде, а эффективному значению. Тогда для получения мгновенных значений проекции нужно умножать на √2.

Для сложения или вычитания двух или нескольких синусоид достаточно геометрически сложить или вычесть по правилу параллелограмма соответствующие символические векторы. Действительно, вектор OI результирующей синусоиды равен геометрической сумме векторов OI₁ и OI₂, составляющих синусоид, так как его проекция на любую ось всегда равна сумме проекций i₁ и i₂ (рис. 24):

 і = i₁ + i₂

Разность векторов OI₁ и OI₂ равна сумме OI₁   и взятого с обратным знаком OI₂ (рис. 25).

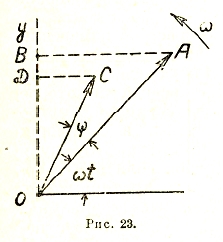
Рис. 23

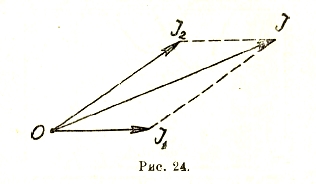
Рис. 24

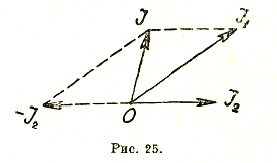
Рис. 25

Начертим векторную диаграмму теоретического генератора, в котором (стр. 260):

Ф₁ = Ф_mах · cos ωt = Ф_mах · sin(ωt+π/2).

e = E_mах · sin ωt

Легко видеть, что вектор магнитного потока опережает вектор наведенного им напряжения на π/2 или 90° (рис. 26).

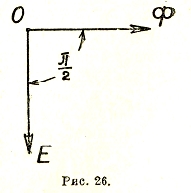
Рис. 26.

Установим, далее, законы прохождения переменного тока через безиндуктивное сопротивление, через индуктивность и через емкость в отдельности.

В безиндуктивном сопротивлении мгновенное значение силы переменного тока устанавливается по закону Ома:  

і = e/r; но е = E_max sin ωt, тогда и i=E_max/r sin ωt = I_max sin ωt, т. е. в этом случае полностью справедлив закон Ома для всех значений тока и в частности для эффективного I = E/r, причем между током и напряжением нет никакого сдвига фаз. Векторную диаграмму см. рис. 27.

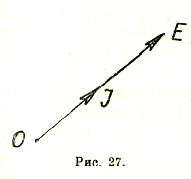
Рис. 27.

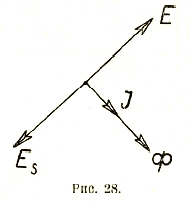
Рис. 28

Иначе обстоит дело в случае индуктивности. Под влиянием внешнего переменного напряжения по катушке потечет переменный ток і, который возбудит в ней магнитный поток, а этот последний вызовет напряжение самоиндукции:

в каждый момент времени равное и противоположное внешнему напряжению. Уже отсюда вытекает векторная диаграмма для данного случая (рис. 28), т. к., согласно предыдущего, ток должен совпадать по фазе с возбужденным потоком, а e_s отстает от потока на 90°. Математически имеем:

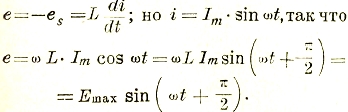
Отсюда: E_max =  ωL · I_m , эффективным значениям:

 I = E/ωL

Мы видим, что формально здесь также имеет место закон Ома; в качестве сопротивления здесь появляется выражение ωL, которое и называется индуктивным сопротивлением и обозначается буквой X_L. При этом сила тока отстает по фазе от внешнего напряжения на 90°. X_L измеряется также в Омах.

При прохождении переменного тока через емкость мы должны вначале найти напряжение на конденсаторе в зависимости от тока. Очевидно, что:

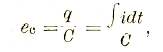
где q — электрический заряд, а С — емкость в фарадах. Тогда, полагая е = е_с и і = І_m sin ωt, находим:

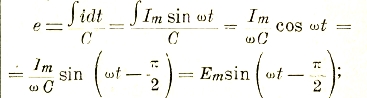
отсюда E_m=I_m/ωC или, переходя на эффективные значения:

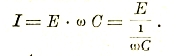
Выражение 1/ωC  формально играет роль сопротивления и называется емкостным сопротивлением (обозначается Х_с). Мы видим, что здесь сила тока опережает внешнее напряжение на 90°.

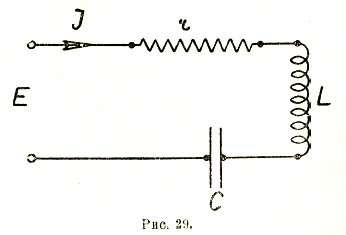
Рис. 29

После разбора отдельных случаев можно перейти к более общему последовательному соединению r, L и С (рис. 29). Очевидно, что в каждом из этих элементов будет падение напряжения, так что баланс напряжений можно написать в следующем виде:

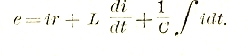
Решение этого дифференциального уравнения относительно i обычными приемами является громоздким. Гораздо проще его решить для установившегося состояния символически, пользуясь векторной диаграммой. Действительно, каждый член уравнения может быть представлен в виде вектора падения напряжения, причем по отношению к току они должны быть ориентированы следующим образом:

Е_r = I₁r совпадает по фазе с I;

Е_L = I₁X_L = І_ωL опережает I на 90°

Е_C = I₁X_C = I 1/ωC отстает от I на 90°.

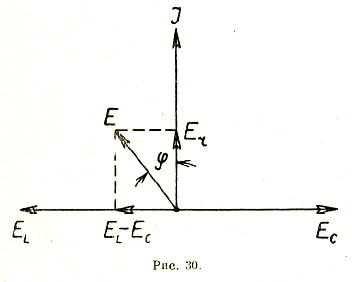
Рис. 30.

Тогда можно построить векторную диаграмму (рис. 30) и из нее

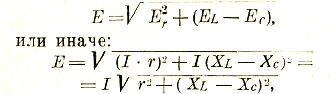
т. е. получаем опять закон Ома:

Выражение

называется полным (или иногда кажущимся) сопротивлением и обозначается буквой Z, так что

I = E/Z

Z измеряется в Омах.

Из векторной диаграммы следует далее, что между током I и напряжением Е получается сдвиг, фаз φ, причем:

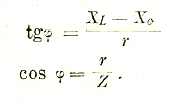
В соответствии с этим одним из решений вышенаписанного дифференциального уравнения, которое справедливо для установившегося режима в цепи переменного тока, является:

i = E_max/Z sin(ωt-φ)

Представляет особый интерес случай, когда X_L =Х_с. Тогда сила тока, как оказывается, зависит лишь от r, а напряжения E_L и Е_С взаимно компенсируются, хотя могут достигать очень больших по сравнению с Е значений. Действительно, возьмем сильно утрированный теоретический пример: Е = 100 вольт; r = 0,1 Ω; X_L = 100; Х_с = 100 Ω. Здесь:

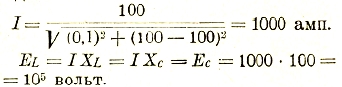
Этот случай называется резонансом напряжений и является опасным в эксплуатации с точки зрения перенапряжений.

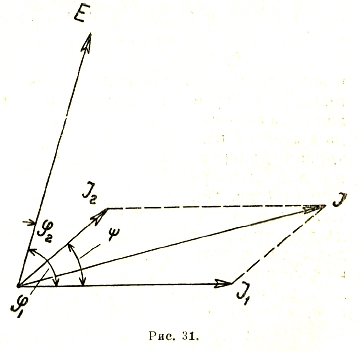
Рис. 31.

При параллельном соединении приходится уже складывать силы токов (рис. 31), причем очевидно, что вектор результирующего тока будет равен

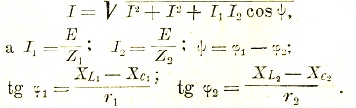
Вместо такого приема можно разложить силы токов на составляющие, совпадающие по фазе с напряжением и сдвинутые относительно него на 90° — т. н. активные и реактивные составляющие тока (рис. 32):

І_а = I₁ cos φ

I_b = I sin φ.

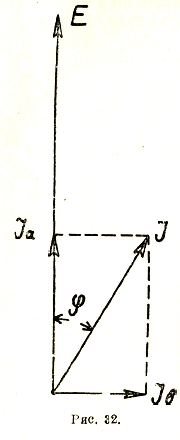
Рис. 32.

Тогда, очевидно, при параллельном соединении:

В связи е этим вводится также понятие об активных g и реактивных b проводимостях. Действительно:  I=E/Z; но пусть 1/Z = y — полной (или кажущейся) проводимости. Тогда: I=E_y. Пусть, далее, аналогично: активная слагающая тока І_a=Еg и реактивная І_b = Еb; отсюда

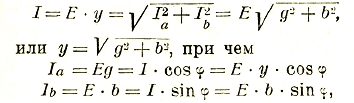
Или g=y cos φ и b=y sin φ;  через сопротивления r и X=X_L-X_C проводимости выражаются следующим образом:

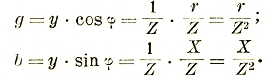
На рис. 33 представлены треугольники сопротивлений и проводимостей. При параллельном соединении индуктивности и емкости особый интерес представляет схема, когда b_L=b_C, т. е.

В этом случае результирующий ток I не имеет реактивной составляющей и, следовательно, совпадает по фазе с внешним напряжением (рис. 34). Это явление называется резонансом токов и широко используется практически для компенсации сдвига фаз.

Мощность переменного тока получится, если перемножить мгновенные значения е и k:

еі = E_m sin ωt I_m sin(ωt-φ)

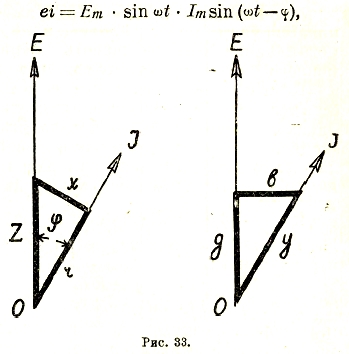
Рис. 33.

что после преобразования приводит к выражению

т.   е. мощность является также переменной синусоидальной величиной, но двойной (2ω) частоты. Приборы, измеряющие мощность (ваттметры), показывают среднее значение:

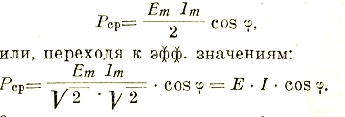
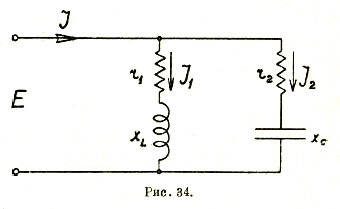
Рис. 34

Это выражение и принимают обыкновенно за мощность переменного тока:

P = EI cos φ

Мы видим, что мощность переменного тока зависит от сдвига фаз. При φ=π/2 мощность равна нулю, т.к. cos φ = 0.

Это дает повод называть cos φ коэффициентом мощности. Заметим, что такое выражение получается только для синусоидальных тока и напряжения. В другом случае войдет еще коэффициент искажения. Итак, мощность переменного тока равна нулю, когда φ = 90° и cos φ = 0, т. е. когда в цепи есть только индуктивность или емкость. Однако, это справедливо только для среднего значения Р; так как в любой момент происходит заряд или разряд L или С, которые содержат энергии:

Li²/2 и Ce²/2.  В соответствии с этим принято различать активную мощность и реактивную:

 и, наконец, полную или кажущуюся мощность El вольтампер (но уже не ватт). В технике сильных токов коэффициент мощности стремятся держать близким к единице, так как от этого зависит рациональное использование активных материалов устройств, рассчитанных на напряжение Е и на силу тока l.

Активная мощность переменного тока может быть выражена еще и иначе:

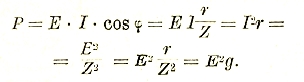
Отсюда и возникло понятие о среднем квадратичном значении е и і как об эффективном.

Символический метод. В векторных диаграммах, употребляемых для изображения синусоидально меняющихся величин, каждый вектор вполне определяется двумя координатами, длиной и фазой, т. е. углом, который составляет этот вектор с осью ОХ (рис. 35). Пользуясь комплексными числами, можно определять вектор при помощи проекций на две взаимно перпендикулярные оси координат, причем проекции на вертикальную ось снабжаются символическим коэффициентом j. Тогда каждый вектор может быть изображен комплексным числом. Например,

Умножению какого-нибудь вектора на коэффициент jn , где n — действительное число, соответствует поворот этого вектора на угол, равный n π/2 против часовой стрелки. Если, например, n = 2, то j² = — 1, и поворот совершается на угол 2 π/2 = π, т. е. на 180°. Такой же результат получается при умножении вектора на ejφ, где φ выражено в радианах.

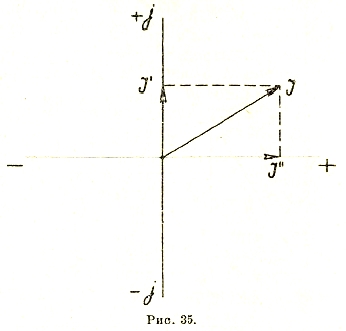
Рис. 35

Символический метод имеет то преимущество, что, пользуясь им, можно все необходимые при решении задач в цепях переменных токов действия с векторами сил токов и напряжения, например сложения и вычитания, нахождения отношения и уравнения, производить аналитически; при этом удобно выражаются не только отношения между амплитудами векторов, но и сдвиг фаз между ними. Особенно это удобно в случаях разветвленных цепей, где приходится составлять системы уравнений.

Все вычисления производятся в соответствии с теорией комплексов, основные положения которой следующие:

здесь r = √ а² + b² — модуль комплекса, или амплитуда изображаемого им вектора, е — основание натурального логарифма; tg φ = b/a — фаза вектора.

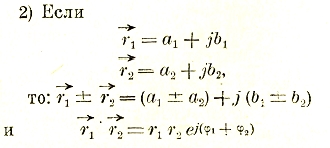
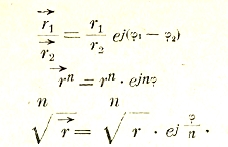
Кроме того, если

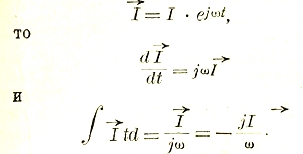
Применяя символический метод к цепям переменных токов, мы получим следующие выражения:

1) Закон Ома

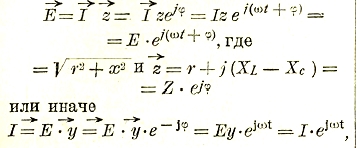
где y — полная проводимость — выражается чрез активную проводимость g и реактивную b следующим образом:

2) Законы Кирхгофа

Эквивалентное полное сопротивление двух параллельных ветвей равно

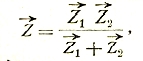
где

 — полные сопротивления этих ветвей.

В то время, как при умножении или делении векторов Е или I на комплексы  или , фазы коих не зависят от времени, мы получаем вектор, вращающийся с той же угловой скоростью, произведение  представляет собой, согласно теории комплексов, вектор, вращающийся с двойной угловой скоростью:

Это выражение не имеет физического смысла. Однако, если заменить один комплексный вектор ему сопряженным, т. е. таким, который отличается лишь знаком перед мнимой частью, то получим:

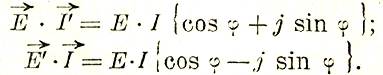
Действительная часть этого выражения дает активную мощность, мнимая же — реактивную, которая в зависимости от того, к какому вектору берется сопряженный вектор (к Е или к I), получает разные знаки. Так как среднее значение реактивной мощности равно нулю, то знак не имеет значения. Однако, если бы условиться считать положительное направление реактивной мощности от источника тока в цепь, то тогда, в случае наличия самоиндукции в цепи, это направление реактивной мощности будет положительным, а в случае емкости — наоборот, отрицательным.

Для обобщения следует заметить, что если при решении какой-либо задачи получается отрицательная активная мощность, идущая от источника, то это следует истолковать так, что в цепи имеется отрицательное сопротивление r, являющееся в таком случае не сопротивлением, как таковым, а, наоборот, источником электрической энергии.

Применение символического метода является неизбежным, когда приходится решать задачу о токораспределении в разветвленной цепи. В этом случае применяются законы Кирхгофа совершенно подобно тому, как для цепей постоянного тока.

В комплексной форме могут быть представлены не только векторы не меняющихся по величине силы тока и напряжения, но и простейшие геометрические места концов меняющихся по величине векторов. Так, например, комплексное уравнение прямой:

Уравнение окружности, проходящей чрез начало координат 0:

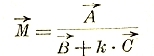
и не проходящей через начало координат 0:

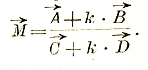
В этих уравнениях  — постоянные комплексные величины, а k — переменная величина.

Метод наложения. Расчет распределения токов и напряжения в цепи с узловыми точками значительно облегчается применением принципа наложения (суперпозиции), который вытекает из линейности уравнений Кирхгофа и согласно которому ток в любой ветви слагается из тех токов, которые получились бы в этой ветви, если бы каждый из источников напряжения действовал во всей цепи в отдельности.

В соответствии с изложенным иногда бывает удобно поступить несколько иначе, а именно: на действительное токораспределение наложить токораспределение, которое получится, если в какой-либо ветви ввести такое напряжение, чтобы в результате в этой ветви ток стал бы равен нулю и ее можно было бы рассматривать, как разомкнутую.

Бывает проще решить задачу относительно измененной схемы (с разомкнутой ветвью) с фактически действующими в полной схеме напряжениями источников и относительно искусственно наложенного напряжения в отдельности. Действительное первоначальное токораспределение получится в результате вычитания найденных токораспределений.

Поясним это па примере с мостиком (рис. 36). Найдем вначале токораспределение, когда диагональ CD разомкнута, т. е.:

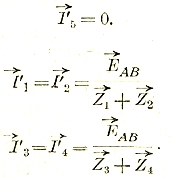
Искусственно накладываемое напряжение должно быть равно и противоположно

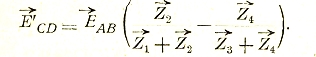
Отсюда, переходя ко второму токораспределению, находим:

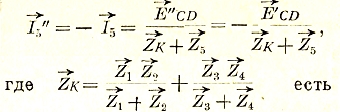
сопротивление коротко замкнутого диагональю АВ (внутренним сопротивлением источника Е_АВ пренебрежем) четырехугольника по отношению к токам СD.

Мы видим, что действительное токораспределение таково:

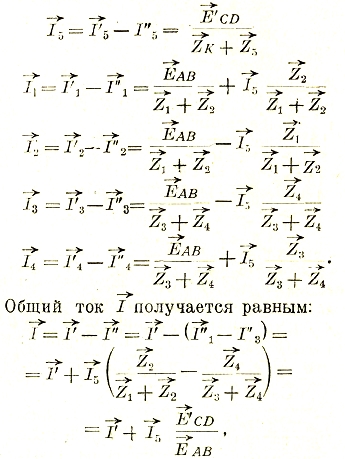
т.е. 79 является суммой тока I₁, возникающего при разомкнутой диагонали CD, и тока I₅, умноженного на отношение

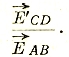
Если последнее выражение помножить на Е_АВ, то мы получим уравнение, говорящее о наложении мощностей:

В схеме фиг. 37, называемой еще всеобщей эквивалентной схемой цепей переменного тока, весьма распространено применение метода наложения двух режимов: холостого хода и короткого замыкания. При этом нагрузка внешней цепи, характеризуемая в схеме полным сопротивлением бывает задана двумя векторами 96, сдвинутыми по фазе на угол φ₂.

Опыт холостого хода (І₂=0) осуществляется при напряжении у вторичных клемм, равном напряжению при нагрузке, т. е. V₂. Опыт короткого замыкания (V₂=0) делается при силе тока во внешней цепи равной І₂.

Тогда V₁ и І₁ при нагрузке, а также и все остальные величины можно, оказывается, выразить через V₂ и І₂:

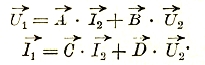
Эти выражения были выведены впервые Брейзигом и поэтому называются уравнениями Брейзига.

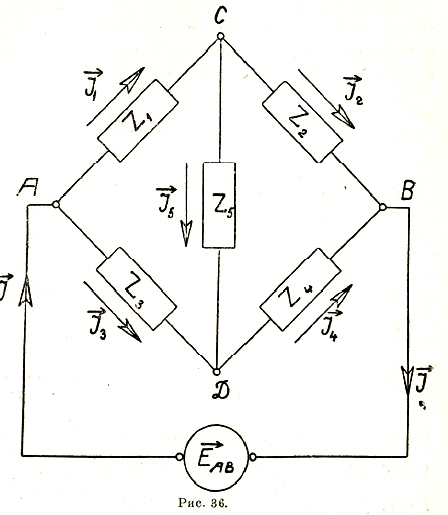
Рис. 36

Метод инверсии. В том случае, когда в цепи не все сопротивления и реакции (постоянные цепи) остаются неизменными, а одно из них меняется, обычно употребляют для исследования графический метод инверсии.

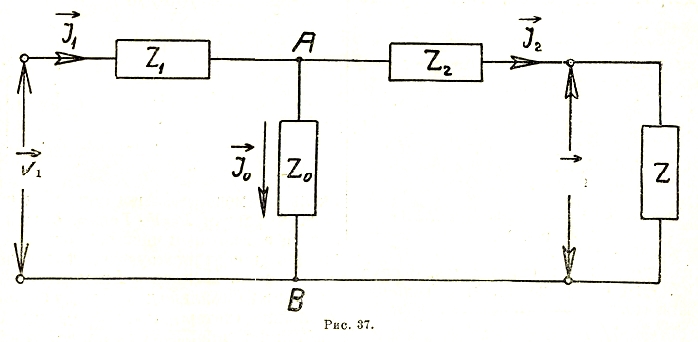
Рис. 37

Этот метод состоит в том, что находят геометрическое место конца вектора тока, или напряжения, при изменении постоянных цепи. Полученные таким образом диаграммы называются соответственно инверсными (или круговыми) диаграммами тока напряжения. Построение обычно значительно облегчается тем обстоятельством, что если концы какого-нибудь вектора, например, имеют простейшее геометрическое место (прямую или окружность), то геометрическим местом обратных векторов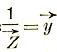    является также простейшее геометрическое место. Действительно, пусть, например,

 (рис. 38а),

где k – числовой коэффициент, могущий меняться от 0 до ∞. Тогда

Нетрудно показать (рис. 38), что конец вектора перемещается по окружности, проходящей через начало векторов и имеющей диаметр, направленный по оси r и равный 1/r действительно при  вектор у имеет максимальную величину = 1/r; что геометрическим местом, концом вектора y является окружность, следует из того соображения, что величина

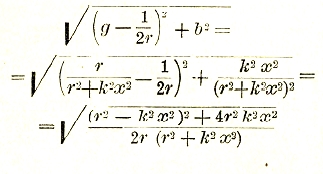
есть величина постоянная, равная √1/2r.

Так как сила тока, то эта окружность является в другом масштабе круговой диаграммой тока.

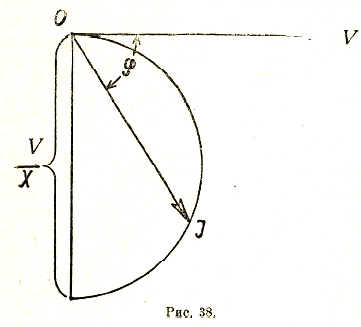
Рис. 38

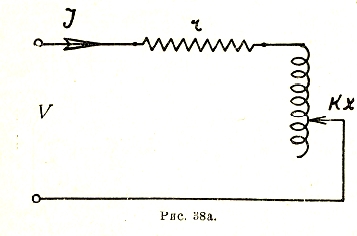
Рис. 38а

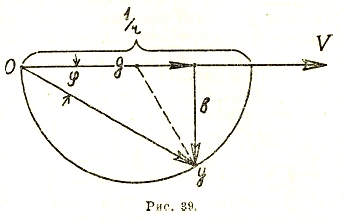
Рис. 39

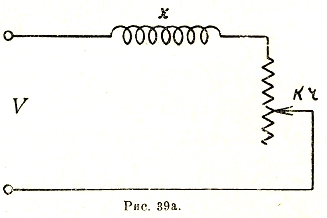
Рис. 39а

Подобным же образом можно показать, что для схемы, изображенной на (рис. 39а), где Z = kr+jx, круговая диаграмма тока имеет вид окружности (рис. 38) с диаметром, расположенным перпендикулярно оси U и равным U/x.

Пользуясь графическим методом инверсии, можно проследить за изменением любой величины, характеризующей цепь переменного тока. Так, например, активная мощность, поступающая из сети и равная Р= V·I cos φ, определяется в некотором масштабе отрезком ординаты соответствующей точки на окружности. Мощность І²r, израсходованная в каком-либо добавочном сопротивлении (потеря мощности), выражается через первые степени активной І_а и реактивной I_в слагающих силы тока. Действительно, уравнение круговой диаграммы в общем случае может быть выражено следующим образом:

(I_a-α)²+( I_в-β)²=R²

где α и β координаты центра окружности, а R радиус окружности. Отсюда:

Из аналитической геометрии известно, что:

есть уравнение поляры окружности относительно начала координат. Лакур показал, что:

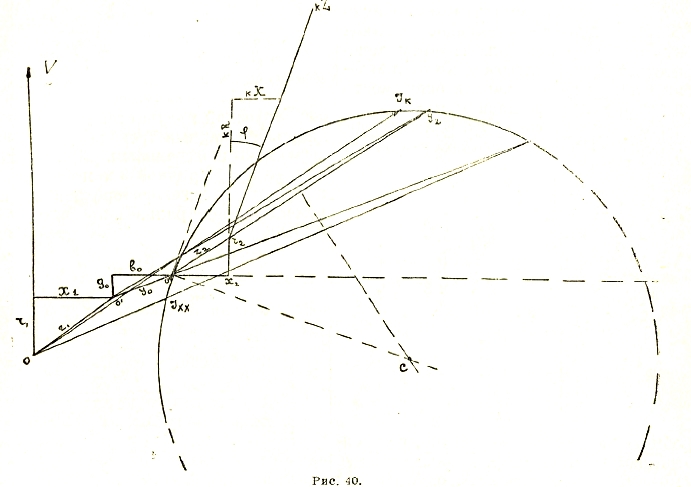
Рис. 40

есть уравнение полуполяры, т. е. линии, параллельной поляре и делящей пополам расстояние последней от начала координат. Таким образом, потери мощности в добавочном сопротивлении пропорциональны расстоянию соответствующей точки окружности до полуполяры.

Для параллельной цепи (рис. 37) круговая диаграмма суммарного тока уже не проходит чрез начало координат, так как здесь суммарная проводимость слагается из постоянной проводимости

В случае, когда перед разветвлением еще имеется некоторое полное сопротивление z₁, круговую диаграмму общего тока получают следующим образом (фиг. 40): 1) проводят прямую сопротивлений z₂, задавшись масштабом для  Х; 2) выбрав новый масштаб, строят окружность проводимости у₂; 3) прибавляют проводимость у₀ в масштабе  у₂; 4) инверсируют окружность у₂ относительно полюса 0’ и получают окружность сопротивления

Причем новый масштаб устанавливается с таким расчетом, чтобы окружность и окружность z совпали; 5) прибавляют сопротивление z₁ в том же масштабе; 6) инверсируют снова окружность z относительно нового полюса являющегося в то же время началом координат, и получают окружность для проводимости у общего тока I₁ масштаб опять устанавливается таким, чтобы окружность для и окружность для совпали; 7) устанавливают масштаб для силы тока, который равен n=Em, если m – предыдущий масштаб для Это значит, что если 1 мм на чертеже соответствует mΩ проводимости, то тот же 1 мм будет соответствовать n=Em ампер силы тока. По окончании построения нужно найти рабочую часть диаграммы, т. е. часть, соответствующую изменению R от 0 до ∞ (от холостого хода до короткого замыкания). Мощность, поступившая в цепь, за вычетом потери в сопротивлении r, отсчитывается тоже от прямой,  определяемой двумя точками на окружности, при которых эта мощность равна нулю. Лакур показал, что эту мощность надо отсчитывать по направлению линии касательной к окружности в точке холостого хода, R₂ = ∞.

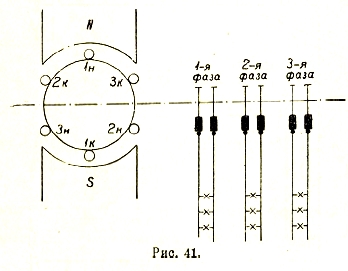
Рис. 41

Многофазные системы. Если в якоре генератора переменного тока разделить обмотку на несколько частей, смещенных в магнитном поле, то каждая часть может быть источником однофазного переменного тока (рис. 41). Напряжения, которые получаются в отдельных частях, будут иметь одно и то же число периодов и будут различаться лишь по фазе. Такую систему называют вообще многофазной системой. Для отдельных частей этой системы, состоящих каждая из источника тока, проводов и нагрузки, часто употребляют не вполне правильное название — «фаза».

Различаются следующие виды многофазной системы: 1) симметричные и несимметричные системы; 2) связанные и несвязанные; 3) уравновешенные и неуравновешенные.

Рис. 42.

Многофазная система является симметричной, когда во всех ее отдельных фазах действуют эдс одной и той же амплитуды, но сдвинутые в двух соседних фазах на один и тот же угол, равный 2π/m, где m — число фаз. Число проводов в несвязанной системе равно 2m. Можно уменьшить вдвое это число проводов, если осуществить соединение фаз многофазной системы многоугольником или звездой (рис.42). Соединение звездой получается, если соединить все обратные провода, в один, называемый нейтральным. При этом в случае симметричной 3-х и более фазной системы в генераторе и в приемнике ток в нейтральном проводе равен нулю:

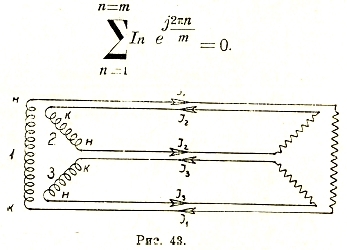
Рис. 43.

Напряжение между фазами при соединении звездой равно геометрической разности фазовых напряжений:

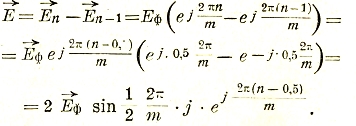
В трехфазной системе (m=3) междуфазовое напряжение равно по величине

и по фазе смещено на угол 30° по отношению к E_n:

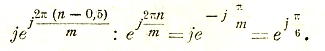
Соединение многоугольником получается, когда прямой провод одной фазы соединяется вместе с обратным проводом смежной фазы (рис. 42). В соединении замкнутым многоугольником сумма фазных напряжений равна нулю:

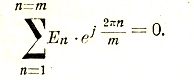
Сила тока в подходящем проводе равна разности токов в фазах:

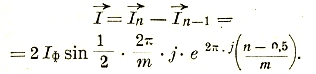
Для трехфазного тока, при соединении треугольником (рис. 43):

Мощность симметричной многофазной системы, в противоположность однофазной, не зависит от времени и является величиной постоянной, равной:

где Е_ф и І_ф — фазовые величины, а φ — сдвиг фаз между ними.

В случае трехфазной системы:

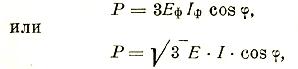
где Е и I межфазовые величины, а φ — по-прежнему сдвиг фаз между фазовыми Е_ф и І_ф.

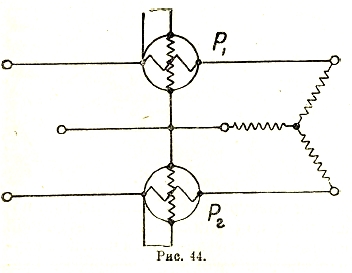
Рис. 44

При измерении мощности трехфазной системы большей частью пользуются схемой Арона (фиг. 44). Векторная диаграмма этой схемы приведена на фиг. 45.

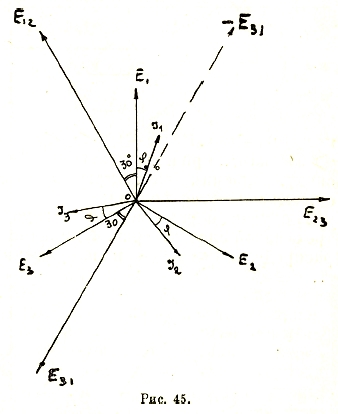
Рис. 45

Измеряемые токи I₁ и I₂ сдвинуты на углы φ от соответствующих фазовых напряжений E₁ и Е₂ (рис. 45). Измеряемые линейные напряжения будут

Вектор -Е₃₁ отстает от I₁ на угол (φ₁—30°), вектор Е₂₃ опережает I₂ на (φ₂+30°). Поэтому ваттметры будут показывать следующие мощности:

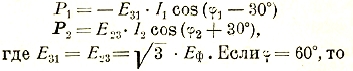
Если φ = 60°, то Р₂ = 0, если φ > 60°, то показание второго ваттметра также будет отрицательным. Для возможности отсчета у односторонних ваттметров делают переключение зажимов. При одинаковой нагрузке всех фаз сумма показаний ваттметров даст общую мощность:

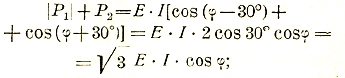
при φ > 60° надо взять разность |P₁—Р₂| так как, далее, при φ <60°

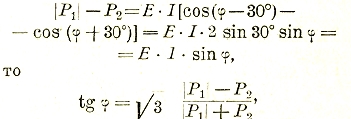
т. е. по показаниям двух ваттметров можно определить угол сдвига фаз.

Интересно, что по построению формулы не требуется знать цену делений этих двух ваттметров, если только они одинаковы (она сокращается). Для установления знака у Р₂ лучше всего предварительно испробовать схему на заведомо омической или чисто индуктивной нагрузке. P₁ относится к ваттметру с большим показанием, если φ лежит между 0 и + 90°. Когда — 90° < φ < 0 или φ > 90° (например, при параллельной работе синхронных машин), ваттметры в этом смысле меняются ролями.

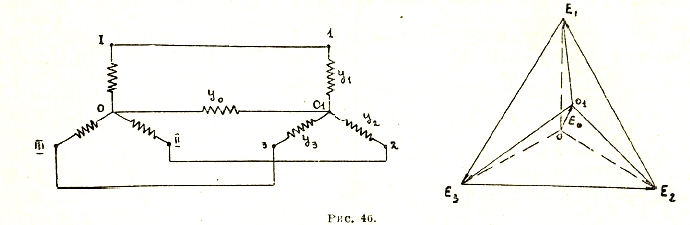
Рис. 46.

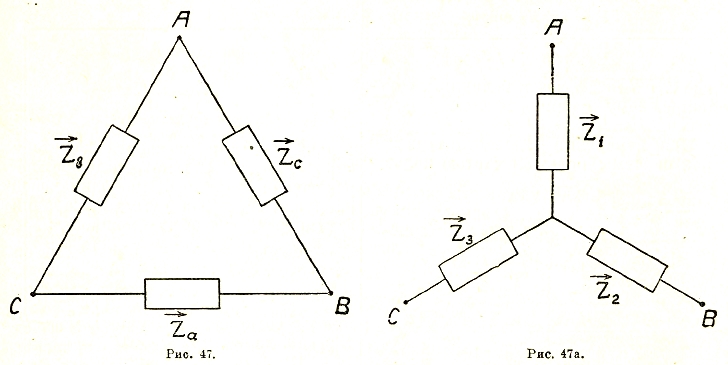
Рис. 17. Рис. 17а.

В случае неравномерной нагрузки трехфазной системы (рис. 46) задача о распределении токов и напряжений в отдельных фазах при соединении звездой в общем сводится к составлению следующих уравнений:

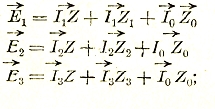
при этом соединение звездой (рис. 47а) может быть приведено к треугольнику (рис. 47) и наоборот на основании нижеследующих уравнений:

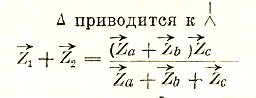
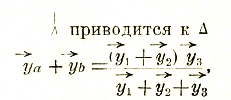
которые могут быть продолжены циклической перестановкой индексов. Когда нагрузкой являются вращающиеся электрические машины, то в последних под влиянием симметричной системы многофазного (в частном случае трехфазного) тока возникает вращающееся магнитное поле с индукцией:

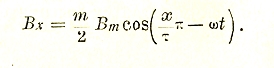
Однако, такое поле получается только при симметричной системе напряжений. При несимметричной системе появляется т. н. обратное паразитное поле. Для определения значения последнего разлагают несимметричную многофазную систему на две симметричные системы с противоположным чередованием фаз, причем большая из них сохраняет первоначальное чередование. На рис. 48 показано сперва сложение двух симметричных систем:

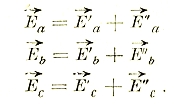
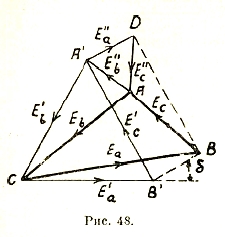
Рис. 48.

На рисунке E”_a=B’B опережает E’_a на угол δ. Так что:

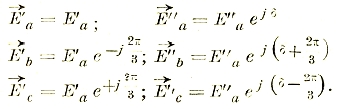
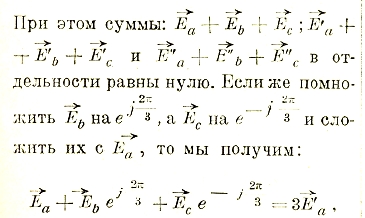
т.е., утроенный вектор E’_a первой симметричной системы. Аналогично этому:

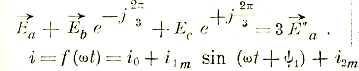
Отсюда вытекают разные способы разложения несимметричной системы напряжения, например, показанный на рис. 49.

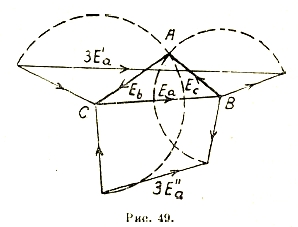
Рис. 49.

В последнее время этот метод исследования приобрел очень важное значение для расчета токов короткого замыкания в электрических установках и выделился в самостоятельный под названием метод симметричных составляющих. При этом он обобщен также и на случай, когда система векторов Е или I не замкнута, т. е. ∑Е≠0 или ∑I≠0. В этом случае выделяется вначале система т. н. нулевой последовательности. Отношение между симметричными системами Е и I соответствующих последовательностей приобретает смысл полных сопротивлений таких же последовательностей.

Несинусоидальные токи. На практике часто приходится иметь дело с кривыми тока и напряжения, более или менее отличающимися от синусоиды, но, однако, сохраняющими свой периодический вид. По Фурье, такие кривые надо представлять себе составленными из основной синусоидальной волны и синусоид более высокого числа периодов, называемых высшими гармоническими составляющими.

Уравнение высшей гармонической n-го порядка имеет вид:

здесь n — произвольное целое число, ω — угловая частота основной волны, nω — угловая частота рассматриваемой высшей гармонической; і_nm — ее амплитуда и ψ_n - ее фазовый угол. Следовательно, уравнение периодической кривой будет:

В технике сильных токов обычно і₀=0, и имеются только высшие гармонические нечетного порядка n = 1; 3; 5; 7; 9; 11... Вместо того, чтобы вводить фазовый угол ψ_n, можно каждую гармоническую разложить на две волны, сдвинутых друг относительно друга на четверть соответствующего периода и имеющих амплитуды а_n и b_n , удовлетворяющих следующим уравнениям:

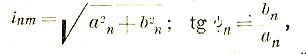
так что уравнение периодической кривой получится в следующим виде:

Для разложения периодической кривой тока или напряжения существует много разнообразных способов, использующих отдельные свойства такой кривой. Имеются также остроумные приборы-анализаторы, при помощи которых можно по форме кривой выделить высшие гармоники.

Здесь представляют интерес лишь два способа:

1. Основной аналитический способ, основанный на том, что среднее значение произведений ординат двух синусоид:

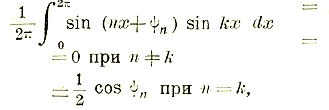
т. е. равно нулю, если эти синусоиды разных чисел периодов, и равно полупроизведению амплитуд (равных в данном частном случае единице) на косинус угла сдвига фаз между синусоидами, если синусоиды одинакового числа периодов (см. выражение мощности переменного тока). Аналогично этому:

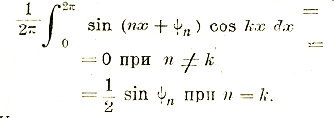
 Находя интегралы

для k = 1; 3; 5; 7; 9; 11;  и т. д., получают возможность отыскать амплитуды A_k  и сдвиг фаз ψ_k для каждой отдельной гармоники.

Способ удобен, когда кривая тока или напряжения может быть выражена в простейшем аналитическом виде.

2. Во всех других случаях можно пользоваться способом Фишер-Гиннена, основанным на том, что если взять алгебраическую сумму k — ординат, расположенных через 1/k часть целого периода кривой, то в этой сумме останутся только ординаты, относящиеся к синусоидам порядка кратного k, а ординаты всех остальных синусоид взаимно уничтожатся. Действительно, сложение ординат несинусоидальной кривой, которые также представляют собой суммы ординат составляющих синусоид, можно заменить геометрическим сложением векторов, изображающих эти синусоиды. Эти векторы вращаются с разной угловой скоростью. Так, например, вектор 3-й гармоники вращается в З раза быстрее, чем вектор основной синусоиды; вектор 7-ой гармоники — в 7 раз и т. д.

Если мы складываем ординаты чрез 1/3 основного  периода, то в этом случае векторы основной синусоиды будут расположены под углами 120° друг относительно друга; вектора 5-й гармоники под углами 5·2π/3 , т. е. 240°; 7-й гармоники 7·2π/3, т. е. 120°. Так как

Рис. 50.

мы берем сумму трех ординат, то ясно, что при таком расположении дадут в сумме нуль три вектора основной синусоиды, три вектора 5-ой, 7-ой, 11-ой и т. д. гармоник. Лишь векторы 3-ей, 9-ой и т. д. гармоник будут сдвинуты на целый собственный период, т. е. дадут тройную сумму значений своих ординат (рис. 50).

Таким образом, деля графически основной период несинусоидальной кривой на 3; 5; 7; 9 и т. д. равных частей (рис. 51а), можно найти:

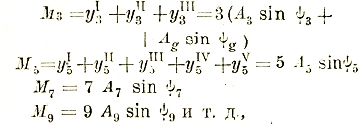
причем ординаты у берутся, исходя из общей произвольной начальной точки t = 0 на оси абсцисс.

Так как этих уравнений недостаточно для того, чтобы определить амплитуды A_k и фазы ψ_k отдельных гармоник, то смещают начальную точку (рис. 51а) на какой-либо известный фазовый угол – лучше всего на четверть основного периода (t₁=T/4) и производят опять такое же сложение ординат. Надо только учесть изменение знаков у ординат отдельных гармоник в соответствии с тем, что:

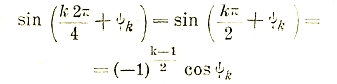
при k-нечетном. Так что

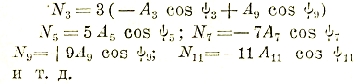
Высшие гармонические составляющие тока заглушаются при наличии в цепи индуктивности – кривая тока приближается к синусоиде. Наоборот, емкость резко искажает форму кривой тока – высшие гармонические (относительно) усиливаются. На фиг. 52 показаны две кривые тока: і_L — при прохождении через катушку самоиндукции, и i_с — при прохождении чрез емкость при одной и той же кривой внешнего напряжения е.

При измерении несинусоидальных токов надо считаться с тем, что эффективное значение периодической силы тока, изменяющейся по произвольной кривой, равно корню квадратному из суммы квадратов эффективных значений отдельных гармоник:

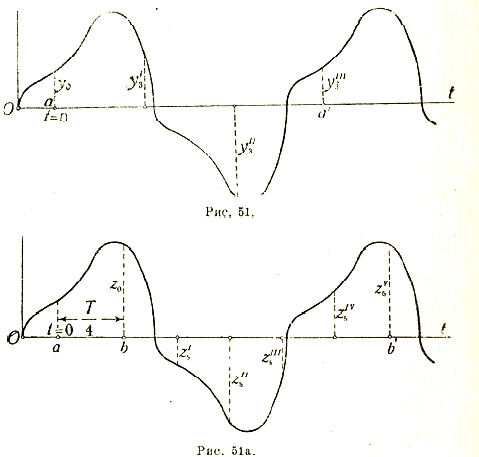
Рис. 50. Рис. 51а.

В трехфазных системах особым свойством обладают гармонические составляющие, кратные 3-м. Так, при соединении звездой генератора в его линейном напряжении всегда отсутствуют гармонические составляющие, кратные 3-м, так как они взаимно вычитаются (фиг. 50). Наоборот, при соединении треугольником они складываются и дают в замкнутой обмотке тройную результирующую величину, вызывая уравнительный ток.

Явления в цепях с железом. Как было показано ранее (на стр. 254), при прохождении переменного тока по катушке самоиндукции в последней возникает реактивная эдс:

Решение этого дифференциального уравнения легко приводит к формуле:

где k-коэффициент формы кривой, равный для синусоиды π/2√2 = 1,11; мы видим, что при данном числе витков w и числе периодов f эта эдс, которая должна быть почти равна по величине внешнему напряжению, тесно связана с величиной Ф_mах. Но для образования последнего необходимо определенное значение намагничивающих ампервитков по уравнению:

Ф = iw/R_μ

где  R_μ — магнитное сопротивление, равное т. е.при данном числе витков необходимо определенное значение силы тока. Этот ток называется намагничивающим.

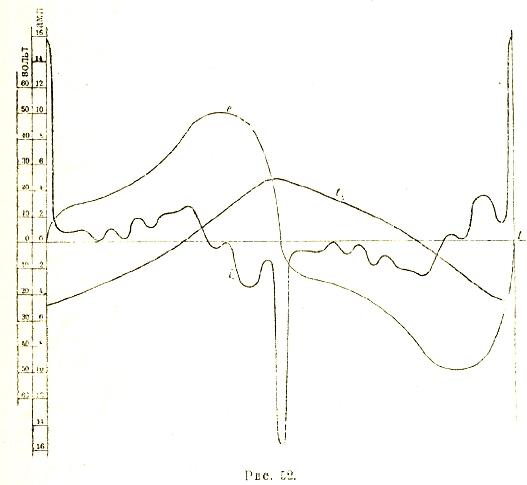
Рис. 52

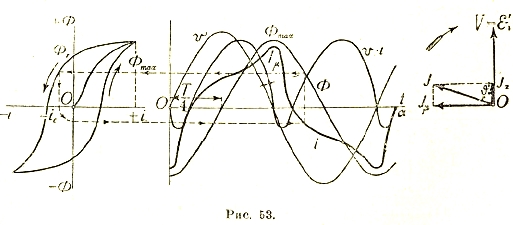
Рис. 53

В электротехнике для уменьшения значения намагничивающего тока используют железные магнитопроводы, в которых магнитное сопротивление значительно меньше, чем в воздухе (μ = 250... 1000).

При употреблении железа, однако, нужно считаться со следующими явлениями: а) кривая намагничивающего тока при синусоидальном напряжении резко отступает от синусоиды (и тем резче, чем больше насыщение железа); б) в железе возникают потери на гистерезис и токи Фуко; в) коэффициент самоиндукции будет переменной величиной, так как μ=f(aw), причем среднее его значение будет падать по мере возрастания насыщения железа; г) возникающие в железе токи Фуко создают свои ампервитки, которые уменьшают магнитную индукцию в средине сечения железа.

На рис. 53 показано построение кривой силы тока при данной кривой намагничивания железа. Построение сделано исходя из того соображения, что при синусоидальном напряжении Е поток Ф должен иметь также синусоидальное изменение по времени. В силу этого намагничивающий ток должен быть несинусоидальным, так как между ним и магнитным потоком нет прямой пропорциональности. Мы видим, что в кривой тока присутствует ясно выраженная третья гармоническая составляющая. Чтобы нанести такой намагничивающий ток на векторную диаграмму, заменяют его кривую эквивалентной синусоидой с тем же эффективным значением. Указанное построение, однако, не учитывало явления гистерезиса, состоящего в том, что перемагничивание железа происходит с некоторым запаздыванием по отношению к фазе намагничивающих ампер-витков,

Если бы между индукцией В и напряженностью поля Н = 0,4πaw не было сдвига фаз, то затрачиваемая на намагничивание объема v энергия, равная

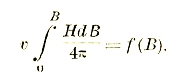
возвращалась бы за каждый период обратно. В действительности же часть этой энергии остается в железе в виде потерь на гистерезис, которые выражаются формулой:

причем по Штейнметцу (для В < 10000) δ=1,6, а опытный коэффициент η в зависимости от сорта железа колеблется от 1 до 5. По Рихтеру  (для В > 10000)δ=2, а η=0,2:1. Для удобства вычислений формуле придают вид:

Потери на токи Фуко в круглом проводе складываются из потерь по каждому элементарному контуру диаметром х (рис. 54),

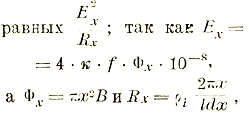
где ρ — удельное сопротивление в 1 см³ объема провода, то:

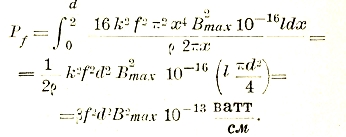
Такая же формула получается и для железных листов прямоугольного сечения.

Для удобства вычисления формуле придают вид:

Здесь Δ-толщина листов железа в мм. Обычно оба выражения потерь на гистерезис и на токи Фуко объединяются в одну формулу:

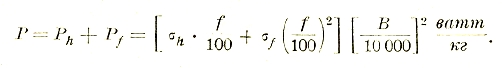
При этом коэффициенты  σ_h и σ_f принимаются равными: для обыкновенного железа σ_h = 4,4-:-4,8; σ_f = 22-:-25; для легированного железа— σ_h =2,4-:-3 σ_f = 4,8-:-5. Разделив вычисленные таким образом потери на приложенное напряжение, находят активную слагающую намагничивающего тока и суммируют ее геометрически с вектором указанной эквивалентной синусоиды реактивной слагающей.

Рис. 54

То обстоятельство, что коэффициент самоиндукции катушки с железом меняется в зависимости от степени насыщения, приводит к следующему явлению в цепи последовательного соединения самоиндукции и емкости. Если в схеме (рис. 55) начать постепенно повышать внешнее напряжение от 0, то сила тока также будет возрастать. Однако, в то время, как напряжение на обкладках конденсатора Е будет увеличиваться по прямой 0D (рис. 55), напряжение у катушки будет зависеть от насыщения и расти по кривой ОВ. Результирующее напряжение (V_L - V_с), равное внешнему, будет идти по кривой ОА.

Рис. 55в

Рис. 56. Рис. 57

Когда внешнее напряжение достигнет значения, соответствующего ординате IA, то мы попадаем в неустойчивую зону кривой ОА, сила тока внезапно возрастает до значения OI’; при этом напряжение на конденсаторе станет больше, чем у катушки, и сила тока изменит на 180° свою фазу по отношению к внешнему напряжению.

Распределение индукции в железном цилиндре, вдоль оси которого проходит переменный магнитный поток (рис. 56), а также плотности тока в проводе (рис. 57), подчиняются уравнениям:

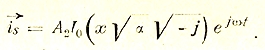
где

А₁ и А₂ – постоянные зависящие от пограничных условий;

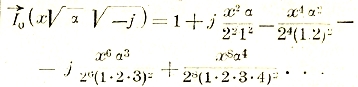
Последнее выражение есть Бесселева функция первого рода нулевого порядка, которая в данном случае может быть представлена в виде:

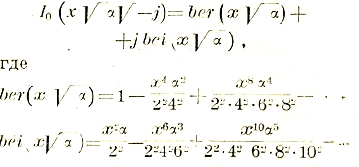
Таблица функций ber x и bei x

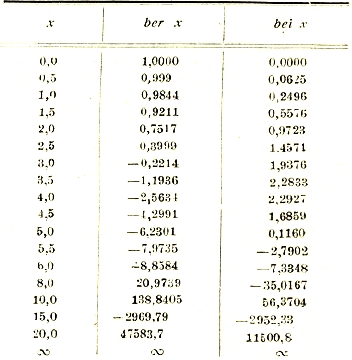
Длинные линии. В сетях высокого напряжения приходится учитывать емкостные явления, так как влияние емкости становится тем больше, чем выше или частота, или напряжение.

Между проводами и между проводами и землей образуется ток смещения, который в проводнике продолжается в виде тока проводимости, называемого зарядным (иногда емкостным) током. Так как емкость в сети является распределенной по длине так же, как и самоиндукция, то сила тока в сети вблизи генераторов имеет иную величину, чем вдали от них. Падение напряжения от реакции самоиндукции и омического сопротивления обусловливает изменение напряжения в сети, что в свою очередь вызывает изменение величины зарядного тока. Образование электрического и магнитного полей связано с определенными потерями энергии, а именно: тепловыми потерями в проводе, потерями на вихревые токи в окружающих проводниках, потерями в различных диэлектриках, примененных в линии, потерями от несовершенства изоляции и потерями на корону.

Основными дифференциальными уравнениями распределения силы тока и напряжения вдоль линии передачи являются следующие уравнения в символической форме:

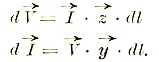
Здесь  — полное сопротивление одной единицы длины какого-либо участка сети; у — полная проводимость единицы длины этого участка.

Для облегчения решения задачи рассматривают обыкновенно неразветвленную линию передачи, приводя ее к одной фазе системы; при этом, а также r и L, g и С считают по длине линии не меняющимися и относят их к одному километру линии.

Полным решением основных дифференциальных уравнений будет:

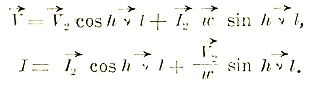
Здесь  – напряжение и сила тока в конце линии а 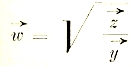 т. н. «характеристика линии», или «волновое сопротивление». Таким образом, зная параметры линии r, x, g, b, а также нагрузку на конце линии V₂ и I₂, можно найти по приведенным формулам распределение напряжения V и силы тока I вдоль линии.

При вычислениях пользуются таблицей гиперболических функций, причем следует иметь ввиду, что:

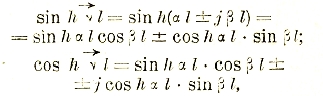
т.е. задача сводится к отысканию гиперболических функций sin h α l и cos h α l и круговых – cos β l и  sin β l.

При этом:

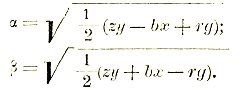
Если линия на конце разомкнута (холостой ход) и I₂=0, то на расстоянии l от конца линии:

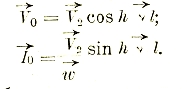
Если, наоборот, линия на конце коротко замкнута (V₂=0), то для того, чтобы в конце была сила тока I₂, напряжение V_k и сила тока I_k на расстоянии v от конца линии должны быть равны:

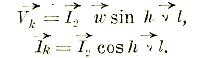
Таким образом, мы видим, что V и l на расстоянии I от конца линии при нагрузке будут равны:

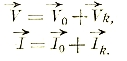
Обстоятельство очень важное при опытных исследованиях линий.

При помощи опыта холостого хода и короткого замыкания можно не только предопределить V и I в том месте, где произведены измерения, но и узнать все параметры линии r, х, g и b, а следовательно и распределение V и I вдоль нагруженной линии. Если вести счет от начала линии, то уравнения для V и I получат вид:

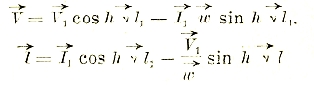
Здесь  – напряжение и сила тока в начале линии, а l₁ – расстояние от начала линии. Пользуясь выражениями:

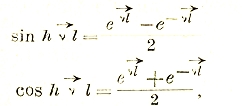
можно предшествующие уравнения написать следующим образом:

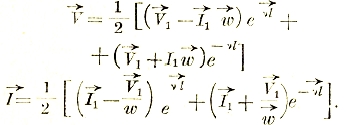
Если взять бесконечно длинную серию, то при l=∞ будут вследствие потерь исчезающе малы (V=0; I=0). Тогда и уравнения получат вид:

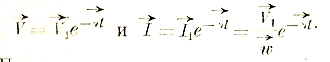
Получаются т. н. прямые волны напряжения и силы тока, т. е. идущие от начала к концу. Действительно:

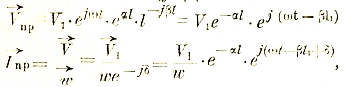
причем мгновенные значения

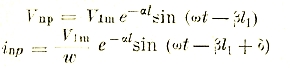
являются в каждый момент синусоидальными функциями расстояния l₁. Начала синусоид, где v_пр = 0 и i_пр=0, перемещаются вдоль линии со скоростью v=l₁/t=ω/β. В линии без потерь

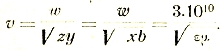
Если линия имеет ограниченную длину l₀ и открыта на конце (холостой ход), то на этом конце происходит отражение волн. Отраженная волна накладывается на прямую, причем первая движется обратно так же, как проходила бы она на продолжении линии за конец ее. Таким образом, расстоянию l₁ от начала линии соответствует путь, пройденный отраженной волной, равный 2 l₀- l₁. При этом волна напряжения отражается с тем же знаком, а волна силы тока – с обратным. Следовательно, напряжение (при холостом ходе) на расстоянии l₁

Для l₁ = l₀, т. е. для конца линии, имеем

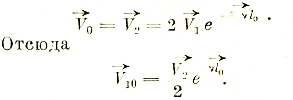
Так что напряжение на расстоянии l₁ от начала линии

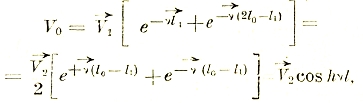
где l – расстояние от конца. Сила тока l₀ на расстоянии l₁ равна:

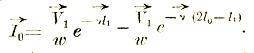
Таким образом, на конце линии l₁ = l₀

l₀ = 0

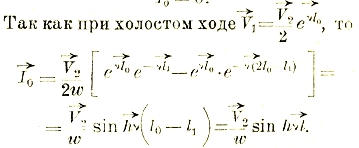
Аналогичным образом при коротком замыкании конца линии, когда волна напряжения отражается с обратным знаком, а волна тока с тем же имеют место следующие отношения:

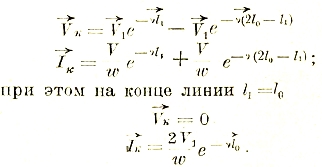
Для того, чтобы сила тока у коротко замкнутого конца равнялась после отражения l₂, не обходимо, чтобы

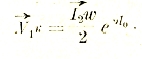
Отсюда для  получаются выражения

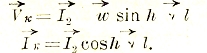
Исследование распределения силы тока и напряжения в длинных линиях может быть произведено опытами на т. н. схемах замещения, т. е. таких искусственных схемах со сконцентрированным омическим сопротивлением, самоиндукцией и емкостью, в которых соотношения между напряжением и силой тока в начале и конце (по величине и фазе) соответствуют действительным соотношениям в линиях. Различают Т-образные и П-образные схемы замещения.

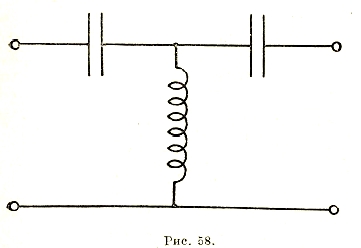
Рис. 58

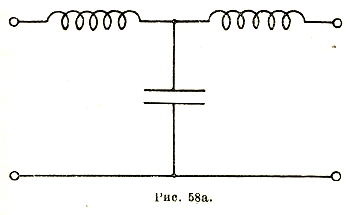
Рис. 58а

Описанная теория относится также ко всем другим случаям цепей с распределенными в той или иной степени равномерными постоянными – к так называемым цепным схемам, например: витки трансформаторов и электрических машин высокого напряжения с учетом емкости между витками и по отношению к корпусу, гирлянда изоляторов и т. п. Применяя описанные уравнения, можно произвести расчет электрических фильтров (рис. 58 и 58а), не пропускающих через себя токи заданной частоты. Соотношение i=V/w позволяет решить задачу о переходе волны с одной линии на другую с различными характеристиками

Пусть, например, ω₂>ω₁. Ток в другой линии не может быть равен току i₁=v/ω₁, а станет меньше. Избыток заряда пойдет на повышение напряжения V₂ в точке перехода, которое становится общим для первой и второй линии. При этом:

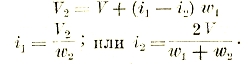
Повышение напряжения и уменьшение тока в месте перехода, являющемся концом первой линии, распространяется к началу последней с такой же скоростью. Происходит, таким образом, отражение волн напряжения и силы тока. Отсюда получается решение для следующих частных случаев:

а) Однородная линия открыта на конце, т. е. ω₂=∞; на основании предыдущего i₂=0, а V_L=2v.

б) Линия коротко замкнута на конце: ω₂=0; естественно, что V₂=0, так что i₂=2V/ω₁=2i₁.

Когда линия замкнута на конце на омическое сопротивление r₂, то:

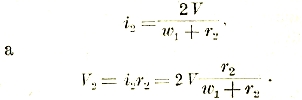
Если r₂>ω₁, то V₂>V; наоборот, когда r₂<ω₁, тогда V₂<V; при r₂=ω₁ и V₂=V, т. е. отражения у конца линии не происходит и режим устанавливается сразу.

Если линия замкнута на самоиндукцию, то в первый момент после подхода волны напряжения и тока к концу i₂=0 и V₂=2V; затем наступает постепенное нарастание тока i₂ по экспоненциальному закону:

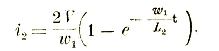
причем

В случае включения на конце емкости в первый момент i₂=2V/ω₁ и V₂=0, а затем i₂ постепенно убывает по экспоненциальному закону:

Когда на конце линии последовательно включены омическое сопротивление r, индуктивность L и емкость С, возможны случаи колебательного или апериодического изменения i₂ в зависимости от того, будет ли больше или меньше . При колебательном изменении:

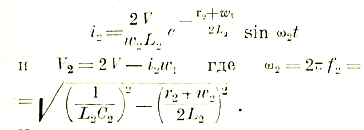
Если период колебания в цепи r₂, L₂, C₂ равен времени прохождения четырехкратной длины линии, т. е. 1/С₂ = 4l/V, то получается резонанс, приводящий к очень высоким перенапряжениям.

Неустановившиеся явления в цепях с сосредоточенными постоянными. Новое состояние, когда в цепи устанавливается ток, принужденно получающий то же число периодов гармонического изменения, как и внешнее приложенное напряжение, устанавливается не сразу. На переход от одного состояния к другому требуется некоторый промежуток времени (время перехода), пока энергии магнитного и электрического полей в цепи не получат значений, соответствующих новому состоянию. В течение времени перехода на последующий установившийся ток накладывается т. н. свободный ток¹⁾. При этом следует различать главным образом два случая. Первый — когда цепь имеет незначительную в сравнении со скоростью распространения электрического тока напряженность (цепи с сосредоточенными постоянными); при этом можно считать, что сила тока в каждый данный момент времени имеет во всех точках одно и то же значение. Поэтому здесь явления рассматриваются главным образом с точки зрения изменения состояния во времени. Во втором случае — протяженность цепи достаточно велика, как, например, уже рассмотренные выше длинные линии передачи энергии. Здесь уже изучение ведется с точки зрения движения по линии электромагнитной волны.

¹⁾ Ранее называвшийся иногда экстратоком.

Для неразветвленной цепи, состоящей из последовательно соединенных омического сопротивления, самоиндукции и емкости, в любой момент времени, независимо от того, успел ли установиться режим или нет, внешнее напряжение распадается на три слагающих:

В переходный период сила тока слагается из установившейся и свободной слагающих: i = i_ст + i_св; точно так же напряжение на обкладках конденсатора: v_с = v_ст + v_св. Поэтому

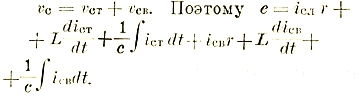
Так как установившийся ток должен удовлетворять уравнению:

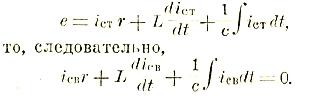
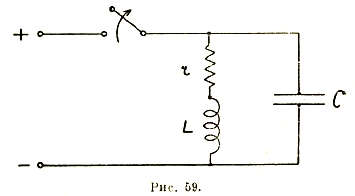
Рис. 59.

Если, например, в схеме, изображенной на рис. 59, разомкнуть рубильник, то в правой части цепи не будет действовать никакого внешнего напряжения. Однако, под влиянием самоиндукции и емкости в этой части возникнет свободный  ток, причем он может быть апериодического или колебательного характера и, вообще говоря, другого числа периодов, нежели принуждающее внешнее напряжение.

Продифференцировав один раз предыдущее уравнение, мы получим после некоторого преобразования:

Полным решением этого уравнения является

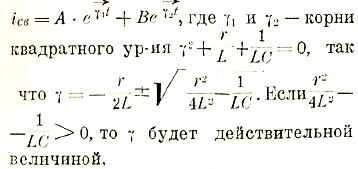
и мы получим апериодическое изменение свободного тока. Сюда относятся также и частные случаи, когда L = 0 или С = ∞.

Если, наоборот, то γ – комплекс вида α+βj и изменение свободного тока будет затухающим колебательным. Число периодов собственного колебания равно

, а множитель затухания

Кривая  представляет собой огибающую, которая касается кривой тока.

В случае, когда С = ∞, т. е. когда конденсатор коротко замкнут, или, проще говоря, его нет, мы имеем апериодическое изменение свободного тока по закону:

причем множитель затухания в два раза больше, чем при колебательном изменении. Если при этом и r = 0, то i_св = i₀ = пост. Точно так же, когда L = 0¹⁾.

¹⁾ При L = 0 для γ получается неопределенное выражение вида ∞=√∞-∞, которое, после раскрытия неопределенности, даст для γ два корня: γ₁ = — ∞ и γ₂ = -1/rC.

При рассмотрении затухания свободного тока удобнее пользоваться величиной обратной множителю затухания α, называемой постоянной времени Т.

Таким образом, Т=1/α. Постоянная времени представляет собой подкасательную в начальной точке экспоненциальной кривой (рис. 60), каковой является кривая апериодического свободного тока при L = 0 или С = ∞, а также огибающая колебательного свободного тока. Действительно:

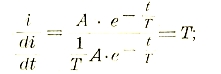
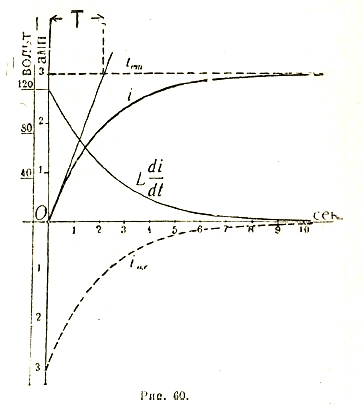
Рис. 60

иными словами, постоянная времени является временем, в течение которого сила свободного тока уменьшается в е раз, т. е. в 2,718 раза. В то время как на характер изменения свободного тока или на число периодов его внешнее принуждающее напряжение почти не влияет, максимальная величина первого находится в полной зависимости от величины этого напряжения в момент включения, выключения или вообще какого-либо изменения. Так, при включении цепи, содержащей r, L и С, на постоянное напряжение, последующий установившийся ток i_ст   будет равен нулю, после того как зарядится конденсатор. Поэтому неустановившийся ток і = i_ст + і_св = і_св. Далее, при t = 0, і = і₀ = 0, так что і = i _св = А + В = 0.

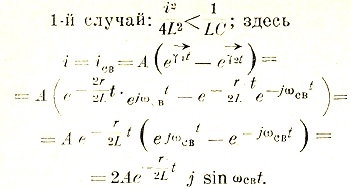
За все время переходного процесса напряжение между обкладками конденсатора подчиняется уравнению:

Подставим это выражение в уравнение:

Мы получим:

или после сокращения на –С и однократного интегрирования

т.е. то же выражение, что и для i_св.

Для нахождения постоянной А в выражении i_св возьмем интеграл:

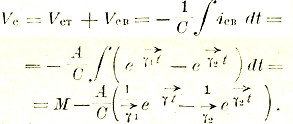
При t = ∞, т. е., когда наступит установившийся режим, напряжение между обкладками конденсатора станет равным и противоположным внешнему напряжению —Е. Поэтому

Наоборот, в первый момент включения

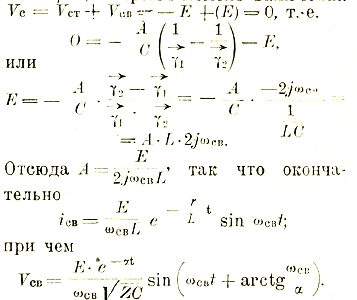
В случае, когда включение происходит на переменное внешнее напряжение E_m sin ωt, свободный ток получается равным:

(см. Круг «Теоретические основы электротехники» или Френкель «Теория переменных токов»), а напряжение на конденсаторе:

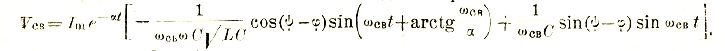
2-й случай: 130. Здесь оба корня γ₁ и γ₂ действительны; так что

где А определяется из уравнения:

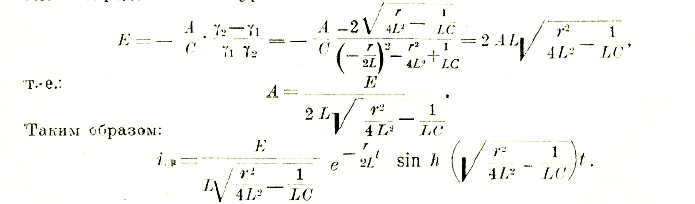
Напряжение на конденсаторе изменится по уравнению:

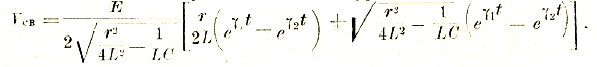
В частном случае, когда С=∞, свободный ток при включении получается равным: при постоянном токе

а при r=0; i_св=∞ и i=∞ - ∞ = E/L t; при переменном токе

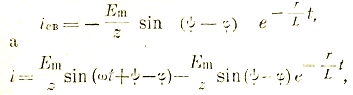
т.е. на установившейся переменный ток накладывается свободный ток, являющийся постоянным током, уменьшающийся по экспоненциальному закону

Точно так же при L=0 свободный ток включения равен при постоянном токе:

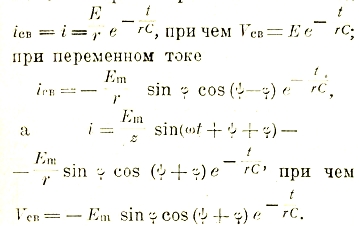
При выключении цепи, содержащей r, L, C, надо считаться с тем, что магнитная энергия Li²/2, запасенная в катушке самоиндукция к моменту выключения, должна частью израсходоваться в образующейся между контактами выключателя вольтовой дуге, а частью сосредоточиться в конденсаторе, причем должен иметь место следующий энергетический баланс:

Если выключение будет i≠0, то оно не может быть мгновенным, так как e_s=-L di/dt было бы бесконечно большой величиной. Сопротивление возникающей поэтому дуги может быть приближенно принято в сумме с сопротивлением цепи, равным

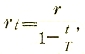, где Т – время выключения; так что уравнение для тока при выключении последовательной цепи r, L, C имеет следующий общий вид:

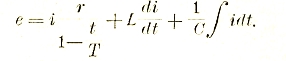
Если бы при переменном токе можно было достигнуть того, чтобы с момента выключения ток дошел до своего ближайшего нулевого значения, изменяясь по той же синусоиде, как и до выключения, то напряжение выключения не было бы выше установившегося. При выключении цепи, содержащей, кроме самоиндукции, еще и емкость, надо считаться с повторным зажиганием дуги, приводящим к тройному напряжению выключении.

Когда цепь содержит несколько электрически связанных контуров, то для рассмотрения неустановившегося процесса в такой цепи надо составить ряд уравнений типа:

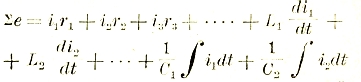
для отдельных контуров, а также уравнений типа ∑i=0 для указанных точек.

Решение уравнений для неустановившегося тока можно провести и в символической форме. Действительно, частным решением уравнения:

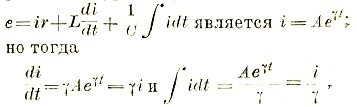
так что можно написать

причем γ по-прежнему должно удовлетворять уравнению

откуда

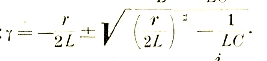
Решение уравнения проводится по формулам Хевисайда для постоянного внешнего напряжения:

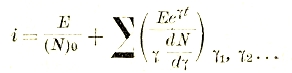и для переменного  i = мнимой части выражения:

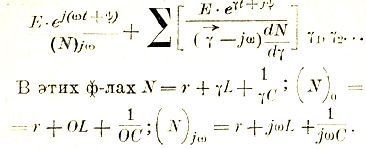
Колебания в связанных цепях. Связь между двумя цепями может быть осуществлена разным образом: чрез общую самоиндукцию, чрез общую емкость, общее омическое сопротивление, чрез взаимную индукцию или одновременно несколькими этими способами. Все случаи решаются также как случай связи чрез взаимную индукцию. Благодаря магнитной связи коэффициенты затухания α', α'' и угловые частоты ω' и ω'' колебаний в обеих цепях становятся уже неравными тем, какие получаются при несвязанных свободных колебаниях:

Дифференциальные уравнения для обеих цепей будут:

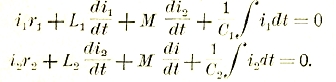
Пользуясь выражениями:

где v₁ и v₂ – напряжения на конденсаторах С₁ и С₂, получают общие решения приведенных уравнений в следующем виде:

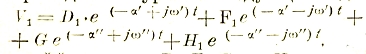
коэффициенты D, F, G и Н определяются по начальным данным колебаний, а α', α'' и ω', ω'' определяются из следующих четырех уравнений:

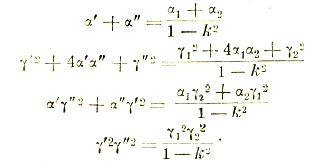
Здесь k — коэффициент магнитной связи, равный

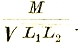
Для решения задачи о колебаниях в двух магнитно-связанных цепях удобно бывает воспользоваться также методом векторных диаграмм, если положить, что мы имеем дело с затухающими гармоническими колебаниями. В таком случае отдельные члены уравнений

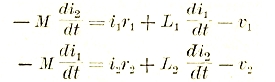
могут быть изображены в виде векторов, складываемых между собой геометрически. Действительно, величина х = Х·е^-αt sin (ωt+ψ) может быть представлена вектором ох, вращающимся с угловой скоростью ω, конец которого перемещается по логарифмической спирали. Ее первая производная, взятая с обратным знаком, может быть представлена вектором, равным по величине и отстающим от вектора Х на угол х = arctg ω/α.

Литература: Круг, К. А.. «Основы электротехники». тт. I и II (1931—1932); Черданцев, И. А., «Теории переменных токов» (1933), Миткевич, В. Ф. «Физические основы электротехники» (1933); Френкель, А., «Теория переменных токов» (перевод с немецкого 1933); Видмар, М., «Научные основы электротехники» (перевод с немецкого, 1932); «Справочник для электротехников» (СЭТ), т. 1 (1928); Ch. Steinmeiz, «Theoretical elements of Electrical Engineers» (1924).

Е. Нитусов.