Энергия

Энергия (греческий ένέργειαιέν — в, έσγον — работа, действие), одна из мер движения и взаимодействия тел; обычно определяется как способность физического тела производить работу (см. работа, XXXIV, 350/59). Энергия — важнейшее физическое понятие; оно имеет огромное теоретическое и практическое значение вследствие существования закона сохранения энергии (см. сохранения энергии закон, XL, 282), относящегося к основным законам природы. Понятие энергии непосредственно связано с понятием о взаимодействии физических тел, являясь одной из основных характеристик взаимодействия. Соответственно различию между видами взаимодействия имеет место различие между видами энергии. Так, например, с механическими движениями связана механическая энергия, с электромагнитными — электромагнитная, с явлениями тяготения — гравитационная и т. д. Однако не следует представлять себе дело так, что все эти виды энергии не связаны друг с другом.

Ценность понятия энергии в том и заключается, что оно позволяет обозреть, разобраться во взаимозависимостях, существующих между самыми разнообразными физическими явлениями. Эти взаимозависимости выражаются в том, что один вид энергии может при определенных условиях превратиться в другой, причём для всей совокупности различных видов энергии справедлив закон сохранения энергии. Сохранение каждого вида энергии в отдельности возможно лишь в том случае, когда рассматривается весьма специальный класс явлений, для которых возможно игнорировать роль других видов энергии.

До XIX в. было известно лишь понятие механической энергии. Общее значение энергии было выявлено в середине XIX в., когда Р. Майер (в 1842 г.), а затем Гельмгольц (в 1847 г.) сформулировали закон сохранения энергии в его общей форме. Однако приоритет в установлении этого основного закона природы принадлежит М. В. Ломоносову (см. XXVII, 364). В работах Гельмгольца этот закон получил трактовку как принцип механического мировоззрения, именно как закон сохранения суммы кинетической и потенциальной энергии. В XIX в. была выявлена роль закона сохранения энергии при описании макроскопических физических процессов в качестве первого  начала термодинамики (см. теплота, XLI, ч. 7, 488). Философское значение понятия энергии и закона сохранения энергии, а также роль закона в естествознании в целом были выяснены в начале восьмидесятых годов прошлого века Фр. Энгельсом.

Идея сохранения движения в общей, философской форме была высказана ещё Декартом. Однако физическая формулировка этого принципа в виде закона сохранения абсолютной величины количества движения тел при их столкновениях и применение этого закона Декартом имело характер одного из следствий его чисто умозрительных построений и мало имело общего с физической реальностью. Закону сохранения количества движения (импульса) системы в дальнейшем была дана правильная формулировка в исследованиях Гюйгенса. Он же впервые открыл закон сохранения живых сил при упругих столкновениях тел.

Идея о сохранении некоторой меры движения и взаимодействия тел в физике XVIII столетия имела вид идеи сохранения и взаимодействия «флюидов». В этот период развития физики предполагалось, что каждое состояние — химическое, тепловое, магнитное и т. д. обусловленной действием особого агента «флюида» — флогистона, теплорода, магнитной жидкости и т. п. Потребовался длительный период исследования, чтобы доказать, что все эти т. н. «невесомые» субстанции в действительности не существуют, что различные формы изменений, происходящих в телах имеют атомистическую основу. Ампер доказал отсутствие особой магнитной жидкости; ещё до него Ломоносов и затем Лавуазье устранили из науки флогистон; наконец, Р. Майер, Джоуль, Клаузиус доказали фиктивность теплорода. Однако идея «флюида» существовала и в дальнейшем, приняв форму идеи эфира, с помощью которого описывали электромагнитные, гравитационные и оптические явления (Фарадей, Максвелл и др.). Наконец, Майер, Джоуль и Гельмгольц установили количественные отношения между различными видами энергии и сформулировали закон сохранения энергии в том виде, как он имеет место и в настоящее время, поскольку возможно отвлечься от релятивистской природы процессов.

Мы рассмотрим здесь механическую энергию и несколько более подробно гравитационные взаимодействия (Об электромагнитной энергии см. электричество; см. также теплота).

Механическая энергия. С механическими процессами, т: е. с движением масс, процессами столкновений и т. п., непосредственно связана кинетическая энергия. Пусть дано тело, о котором мы предположим, что оно не связано с другими телами, т. е. может свободно двигаться в различных направлениях. Пусть это тело отнесено к некоторой системе отсчёта и имеет, таким образом, координаты х, у, z, ct, где х, у, z — пространственные координаты тела, а t — время, с — релятивистская константа, имеющая размерность скорости и равная

В любой инерциальной системе отсчёта между энергией Е этого тела и его импульсом р имеется соотношение:

где постоянная, стоящая справа, не зависит от выбора той или иной инерциальной системы отсчёта. Если мы  выберем систему отсчёта так, что в ней импульс тела равен нулю:

т. е. перейдём к системе, движущейся  вместе с телом, то в такой системе отсчёта будет:

чем и определяется физический смысл инварианта (2) как энергии тела в движущейся вместе с ним системе отсчёта (иначе называемой собственной энергией тела, или энергией покоя). Константа справа в (2) равна m²₀c², где m₀ — масса покоя; так что

Это соотношение, устанавливающее эквивалентность массы и энергии, является одним из важнейших положений современной физики.

Уравнение (2), т. е. уравнение

можно переписать в виде:

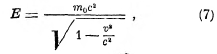
если вместо импульса р ввести скорость v, пользуясь соотношением

Пусть имеется N тел, движущихся относительно данной системы отсчёта со скоростями v₁, v₂…, v_N. Пусть они имеют энергии

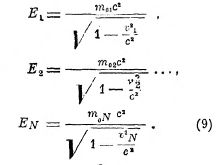
Закон сохранения энергии для этих тел, которые мы рассматриваем как независимые от внешних влияний, может быть сформулирован в следующем виде: запас энергии системы, не подверженной  внешним энергетическим воздействиям, остается с течением времени постоянным. При этом сейчас же возникает вопрос о пространственно-временной характеристике такой системы и введении для неё общего времени и соответствующей системы отсчёта, в которой формулируется закон сохранения. Это связано с тем, что закон сохранения энергии всегда должен быть дополнен законом сохранения импульса р. Каждая из упомянутых частиц имеет импульс, равный

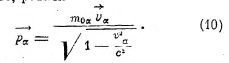
Закон сохранения импульса гласит, что суммарное значение импульса

сохраняет с течением времени постоянное значение.

Равноправность систем отсчёта в релятивистском смысле выражается существованием релятивистки инвариантного закона сохранения энергии и импульса:

(если рассматривать задачу в рамках специальной теории относительности), где τ_i – компоненты энергетического релятивистского вектора. Рассматривая все эти N не взаимодействующих частиц в качестве материальной системы, мы можем выбрать систему отсчета так, что в ней результирующий импульс (11) равен нулю:

По предыдущему мы можем написать в этой системе отсчёта для энергии Е всей системы:

где М₀ — масса всей системы. Если v_0α — скорость α-ой частицы в этой системе отсчёта, то:

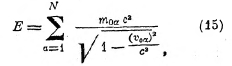
так что покоящаяся масса всей системы частиц равна:

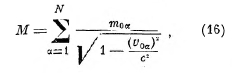
т. е., не равна сумме

покоящихся масс, а зависит от их скоростей. Эго означает, в частности, что газ при нагревании становится тяжелее, так как его масса увеличивается. Величина  Δ = М — (m₀₁ + m₀₂ … + m_0V) называется дефектом массы. Если система движется как что легко доказать, пользуясь лоренцевским преобразованием, т. е. перейдя от системы отсчёта, в которой система покоится, к системе, движущейся но отношению к ней со скоростью v, то она обладает энергией

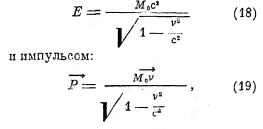
что легко доказать, пользуясь лоренцевским преобразованием, т. е. перейдя от системы отсчета, в которой система покоится, к системе, движущейся по отношению к ней со скоростью v.

Если скорость тела мала в сравнении со скоростью с, так что можно пренебречь высшими степенями отношения v/c в сравнении с единицей, то тогда выражение для энергии Е получает вид:

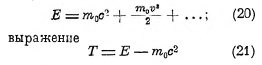
называется кинетической энергией. Для малых скоростей

для любых же скоростей (меньше с, конечно):

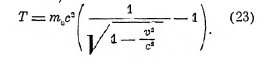
Простейшим — с энергетической точки зрения — механическим процессом является упругое столкновение двух тел. Как показывает опыт, этот процесс всегда происходит с выполнением законов сохранения энергии и импульса, а именно, если Т₁ и Т₂ и  — энергии и импульсы тел до столкновения, а  — после столкновения, то всегда:

Как показывают эти уравнения, процесс столкновения можно описать, задав восемь независимых величин, за каковые можно выбрать, например,  и полярные углы, определяющие направление импульса р’₁ в системе отсчёта, центр которой движется вместе с центром инерции сталкивающихся тел. Эта система отсчёта очень удобна при исследовании столкновений, так как в ней сталкивающиеся тела лишь изменяют направления импульса, сохраняя их величину. В этой системе результирующий импульс равен нулю.

Более сложным процессом является неупругое столкновение, при котором происходит изменение собственной энергии сталкивающихся тел. Этот процесс имеет место при столкновении сложных систем, состоящих из отдельных составных частей, энергетически связанных, или при условиях, когда происходит трансформация одних частиц в другие. При неупругом столкновении происходит изменение связей между компонентами сталкивающихся систем, т. е. часть энергии переключается на эти изменения. Законы сохранения энергии и импульса и здесь являются основным руководящим принципом.

Исследование механических процессов приводит к заключению, что характеристика их посредством кинетической энергии и импульса недостаточна, так как взаимодействия существенным образом зависят от взаимного расположения рассматриваемых физических тел. К формулировке этой зависимости мы и перейдём.

В рамках старой механики Ньютона — Лагранжа средством решения задач о взаимодействии частиц было представление о силах, действующих на массу частицы. Примитивная, но весьма разработанная математически теория, не вникая в существо взаимодействия, принимала  за основу, что величина механической силы, развивающейся между удалёнными друг от друга частицами, определяется, прежде всего, их взаимным положением для одного и того же момента времени. Иными словами, энергетические соотношения в системе из N частиц определяются, во-первых, их скоростями и массами — через кинетическую энергию и, во-вторых, мгновенной конфигурацией системы — через потенциальную энергию U. Пусть рассматриваемые нами взаимодействующие частицы помещены в точках, определённых радиус-векторами

Пусть затем они перемещаются в точки

Тогда возникают следующие энергетические соотношения. Классическая механика имеет дело с обратимыми процессами и, соответственно этому, понятие механической энергии не зависит от параметров, определяющих процесс перехода из одного состояния в другое, а только от параметров, определяющих начальное и конечное состояние системы (с этой точки зрения введение понятия о связях — голономных и неголономных — представляет собой обобщение, непосредственно связанное с введением термодинамических понятий).

В простейшем случае, когда силы имеют потенциал, мы можем написать между А — работой внешних сил, А = ∑Fdz, изменением кинетической энергии системы Т и потенциальной U, следующее соотношение:

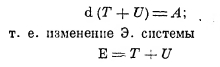
равно внешней работе, положительной («против системы» или в «направлении внешней силы») или отрицательной («совершаемой системой» или «против внешней силы»).

Для системы, состоящей из N частиц, следует различать полную потенциальную энергии системы и потенциальную энергии одной частицы, возникающую благодаря воздействию других; т. е. для потенциальной энергии нет аддитивности. Так, например, если имеется N частиц, взаимодействующих по закону Кулона, т. е. с силой, обратно пропорциональной квадрату расстояния, причем N₁ из них отталкиваются между собой, но притягиваются каждой из остальных (N—N₁), также отталкивающихся между собой, то потенциальная энергия отдельной частицы, k-ой, даётся выражением:

 N—Nx

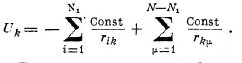
Полная потенциальная энергия такой системы равна:

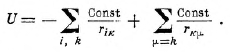
Случаи взаимодействия с силами, обратно пропорциональными квадрату расстояний, мы имеем, во-первых, в притяжении масс (гравитационное взаимодействие ср. тяготение, XLII, 1/8), и, во-вторых, в электростатике. В первом случае имеет место только притяжение, во втором — притяжение и отталкивание (ср. электричество, LII, 10 сл.).

Понятие потенциальной энергии вначале непосредственно было связано с концепцией дальнодействия, которая лежит в основе механики Ньютона—Лагранжа. Однако уже во второй половине XIX в. выяснилось, что концепция дальнодействия несостоятельна, в частности, уже потому, что в её рамках, собственно, и не может быть поставлен вопрос о физическом существе процесса передачи взаимодействия между удалёнными друг от друга телами. И действительно, делавшиеся в огромном числе попытки рассмотреть понятие потенциальной энергии, оставаясь в пределах механики Ньютона, все оказались безуспешными. То обстоятельство, что, несмотря на принципиальную несостоятельность этой концепции, всё же очень большая группа физических явлений может быть хорошо исследована и с помощью этой теории, объясняется тем, что скорость передачи взаимодействия чрезвычайно велика в сравнении со скоростями масс, фигурирующих в этих явлениях, и, таким образом, может считаться как бы бесконечно большой. Но при более точном анализе взаимодействий выясняется необходимость перехода к более последовательной теории, которая позволяла бы правильно учесть конечную скорость передачи взаимодействия — с. Таким образом, в теорию взаимодействия, в формулировку зависимости энергетических соотношений должна существенным образом входить скорость с, и это ведёт к пересмотру понятия потенциальной энергии. Эта проблема была рассмотрена уже в 1858 г. Б. Риманом (см.), исследовавшим вопрос о том, каким уравнением должно быть заменено основное уравнение электростатики — уравнение Пуассона (см. LII, 44/47), — если мы учтём скорость передачи взаимодействия. Решение этой задачи, однако, было достигнуто лишь более полвека спустя в теории относительности А. Эйнштейна (см.). Было выяснено, что передача взаимодействий, лежащая в основе понятия потенциальной энергии старых механических теорий, осуществляется как непрерывный процесс, от точки к точке, со скоростью с, независимо от выбора системы отсчёта, относительно которой фиксируется эта скорость. Скорость эта оказалась существенным образом связанной с основными свойствами пространственно-временной координации физических явлений. В то время как во всех других случаях скорость определяется по расстоянию и времени, в которое пройдено это расстояние, в данном случае время определяется по расстоянию и по скорости с. При этом принципиальное значение имеет то, что эта скорость одинакова во всех инерциальных системах отсчёта (релятивистская инвариантность с).

С математической точки зрения переход от приближенной теории дальнодействия к теории взаимодействия, распространяющегося от частицы к частице с конечной, инвариантной скоростью с, состоит в переходе от уравнения эллиптического типа (уравнение Лапласа—Пуассона), определяющего зависимость потенциала от координат, к уравнениям гиперболического типа, а именно — к уравнению Даламбера, т. е. к уравнениям, имеющим вещественные характеристики. Это значит, что интегралы этого уравнения описывают — при геометрической интерпретации — движущиеся поверхности, по разные стороны которых сосуществуют различные физические состояния среды; именно, по одну сторону от поверхности возбуждение еще не возникло, а на другой оно уже имеется. Возможность такого сосуществования определяется тем, что для данного типа уравнений оказываются выполненными на упомянутых поверхностях условия непрерывности, наложенные на величины, характеризующие энергетическое состояние тел в зависимости от их взаимного пространственно-временного положения. Эти движущиеся поверхности и являются не чем иным, как фронтами волн действия, распространяющегося со скоростью с во все стороны от действующей частицы.

Таким образом, в более развитой теории понятие потенциальной энергии, определяющейся мгновенной конфигурацией взаимодействующих частиц, уступает место понятию о возмущении, распространяющемся во все стороны с инвариантной скоростью с по всем направлениям от частицы, создающей это возмущение. Более точный физический смысл этого положения может быть выяснен после рассмотрения тех изменений, которые претерпевает понятие потенциальной энергии при переходе к более точной теории.

Рассмотрим, прежде всего, гравитационные взаимодействия. Пусть даны две массы m₁  и  m₂, находящиеся на расстоянии r₁₂ друг от друга. Между этими массами развивается механическая сила f₁₂, пропорциональная им и обратно пропорциональная квадрату расстояния между ними. Изменение взаимного положения этих масс связано с совершением некоторой положительной или отрицательной механической работы и, следовательно, связано с изменением потенциальной энергии, определяющей силу этого (гравитационного) взаимодействия. При ближайшем рассмотрении этой проблемы выясняется существенная, принципиальная зависимость гравитационного взаимодействия от кинематических, пространственно-временных соотношений. Ситуацию, имеющую место в данном случае, можно охарактеризовать следующим образом.

Пространственно-временная координация физических событий выражается соотношениями физической геометрии, т. е. соотношениями, существующими между реальными масштабами, часами, системами отсчета и т. д. Следует проводить различие между пространственной геометрией и геометрией пространственно-временных соотношений. Первая является лишь весьма частной специализацией последней. В дальнейшем речь идет все время о последней. Далее, следует различать геометрию естественную и геометрию абстрактную. Последняя является геометрией, реализованной выбранными масштабами, и произвольно выбирается в данной пространственно-временной области. Обычно это геометрия Евклида в пространственных соотношениях и геометрия Минковского (см.) в пространственно-временной области. Естественная геометрия выражает метрические соотношения, реально существующие в данной области. Расхождение, если оно имеется, между пространственно-временными соотношениями, реально существующими в данной области (естественной геометрией), и геометрией Минковского (т. е. абстрактной геометрией) осмысливается как наличие силового поля. Это расхождение и лежит в основе понятия силового поля, т. е. понятия потенциальной энергии. Если, например, в данной пространственно-временной области существуют соотношения такие, как вблизи гравитационной массы, то в ней геодезической линией будет кривая, именно та линия, по которой движется, например, планета вокруг Солнца, тогда как по приписываемой этой области абстрактной геометрии геодезической линией будет прямая. Факт движения по кривой и осознается как наличие потенциального гравитационного поля. Потенциальная энергия гравитационного поля определяется отличием реально существующих (физико-геометрических, а именно метрических) соотношений от метрики мира Минковского, с которой всегда отождествляются геометрические (точнее чисто-кинематические) соотношения. Это легко показать сравнением пространственно-временных интервалов ds². Для этого мы должны рассмотреть более общие свойства гравитации.

Общая форма пространственно-временного интервала определяется, как известно (ср. теория относительности, XLI, ч. 7, 424/26), метрическим тензором:

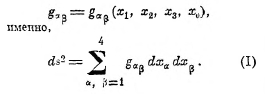
Компоненты тензора g_αβ определяются как функции пространственно-временных координат х₁, x₂, х₃, х₀, являющиеся решениями дифференциального нелинейного уравнения в частных производных второго порядка — уравнения гравитационного поля:

найденные А. Эйнштейном.

Здесь, R_μν —свернутый тензор кривизны, R —инвариант кривизны, T_μν — тензор, определяющий распределение энергии-материи, х — константа, связанная в нерелятивистском приближении с ньютоновской гравитационной константой  γ,

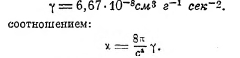
Величины R_μν зависят от g_αβ и их частных производных.

Уравнение (II) — основное при исследовании энергетических проблем. Мы имеем ввиду первый вариант теории Эйнштейна; в дальнейшем имели место различные обобщения, в частности, космологического характера. Особое значение имеют следующие два его свойства: во-первых, оно ведёт к формулировке законов сохранения энергии - материи, точнее говоря, вид левой части уравнения обусловлен существованием этих законов (см. далее), и во-вторых, уравнение определяет законы движения масс.

А. Рассмотрим сначала второе следствие. В старой ньютоновской механике проблема движения масс в поле тяготения рассматривалась с точки зрения двух независимых друг от друга положений: а) касающихся движения массы под влиянием внешних сил; б) касающихся источников этих сил.

Первая проблема математически формулируется уравнением движения:

где  φ — Ньютонов потенциал гравитационных сил:

который вычисляется (вторая проблема) по уравнению Пуассона:

(ρ — плотность масс). Связь обоих положений в старой теории совершенно не ясна. При более глубоком (релятивистском) анализе этого цикла проблем выясняется, что эти задачи имеют специфически-релятивистскую природу, а именно вся задача в целом должна быть поставлена как задача определения решений уравнения для уравнения (II), для данной области пространственно-временного континуума. Найденные интеграцией уравнения (II) g_αβ по подстановке их в выражение для интервала (і), определяют метрику данной области, т. е. законы, имеющие место для всех возможных передвижений или иных пространственно-временных соотношений.

Уравнение (II) нелинейно, и задача определения его решений — g_αβ — выглядит следующим образом. Нужно задать характер движения, точнее — пространственно-временное распределение масс в исследуемой области, т. е. говоря математически, задать компоненты тензора энергии-материи Т_αβ в качестве функций от x₁, x₂, х₃, х₀. Это позволяет найти g_αβ, входящие в R и R_μν (также и через производные первого и второго порядка). Найдя g_αβ как функции x₁, x₂, х₃, х₀ и подставив найденные g_αβ в (1), мы получим выражение для интервала и тем самым найдем метрические соотношения в данной области. Законы их изменения при переходе от одной системы отсчета к другой определяются тем, что g_αβ — тензор, а ds — инвариант.

Однако такая постановка задачи возможна только в случае, когда возможно пренебречь реакцией поля на массы; вообще же расчленение задачи на задачу задания Т_μν и последующего определения g_αβ интеграцией уравнения невозможно. Т_μν следует рассматривать как составную часть уравнения, характер зависимости которой от метрики g_αβ определяется тем, что по подстановке g_αβ удовлетворяющих уравнению, оно тождественно удовлетворяется. Иначе говоря, распределение масс и их движение (пространственно-временное распределение) однозначно определяется метрикой данной области, последняя же, в свою очередь, однозначно определена пространственно-временным распределением масс. То, что уравнения (II) имеют такой характер, должно быть доказано непосредственной их интеграцией. Это и было показано А. Эйнштейном и Громмером в 1927 г.

Как эти исследования, так и более поздние, показывают, что упоминавшиеся выше две независимые классические задачи на самом деле непосредственно связаны. Они становятся независимыми только при переходе к нерелятивистской постановке, которая настолько искажает действительное положение вещей, что нельзя усмотреть нужные связи.

Смысл перехода к нерелятивистскому пониманию метрических соотношений, связанному с введением понятия потенциальной энергии, состоит в следующем.

Предполагая, что в первом приближении в рассматриваемой области имеет место метрика мира Минковского, т. е. g_αβ имеют значения g_αβ = —δ_αβ (т. е.  для  α≠β, g_αβ = 0; для α = β, g_αβ равны соответственно — 1, — 1, — 1, + 1), переходим ко второму приближению, считая, что g_αβ можно написать в виде

где функции γ_αβ столь малы по сравнению с первым членом, что можно пренебречь высшими степенями этих функций и их производных.

В так получающемся приближении и содержатся законы механики и теории тяготения Ньютона, если пренебречь зависимостью g_αβ от х₀; а именно, расчёт показывает, что тогда функции

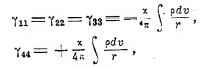
остальные γ_αβ равны нулю. Подставляя полученные γ_αβ в ds² мы получим следующее выражение для этого инварианта:

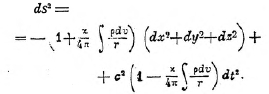
С другой стороны,  уравнение (II) приводит к уравнению Пуассона, позволяющему интерпретировать γ_αβ как потенциал. А именно, получается, что уравнения движения имеют вид

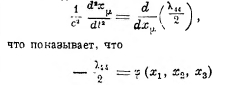
имеет смысл Ньютонова потенциала тяготения. Эти результаты и выясняют полностью смысл понятия потенциальной энергии гравитационного поля, как понятия, непосредственно выводимого из комплекса метрических соотношений общей теории относительности.

Б. Рассмотрим теперь второе основное следствие закона гравитации (II), а именно формулировку законов сохранения энергии-материи. Чтобы получить таковую, следует разыскать интегральные и дифференциальные законы сохранения. Интегральные законы могут быть получены из дифференциальных. Дифференциальная формулировка законов означает, что они учитывают непрерывную передачу взаимодействий от точки к точке с конечной скоростью с.

В таком случае достигается, как известно, формулировка законов, независимая от выбора той или иной системы отсчёта.

Левая часть уравнения Эйнштейна, т. е. комбинация величин R_αβ и R

обладает тем основным свойством, что она сохраняется во всех допустимых системах отсчёта. Эго утверждение следует понимать следующим образом.

Если взять нерелятивистский предельный случай, то закон сохранения непрерывной  векторной функции выражается, как известно, условием равенства нулю «расходимости» ее, т. е. уравнением

Обобщение, которое должно быть осуществлено при переходе к величинам, изменяющимся с течением времени, может быть найдено в рамках специальной теории относительности, а именно исследованием инвариантности по отношению к преобразованиям Лоренца. Исследование показывает, что три величины А_х, A_y, A_z, образующие компоненты вектора по отношению к преобразованиям чисто пространственным, не дают полной характеристики, и что к ним должна быть добавлена четвёртая величина А₀. Тогда совокупность четырёх величин

описывает данное векторное поле релятивистски-инвариантно. Закон сохранения (β) обобщается при этом в закон релятивистски-инвариантный

Это уравнение и выражает векторный релятивистски-инвариантный закон сохранения. Однако энергетические соотношения для случая гравитационного поля выражаются не уравнением (III), а тензорным уравнением, выражающим требование, чтобы комбинация величин (II*), называемая тензором энергии-материи, сохранялась во всех системах отсчета, т. е. чтобы релятивистская расходимость этого тензора тождественно равнялась нулю.

Если обозначить через

величину, называемую тензорной плотностью (количество выражаемой этим тензором величины, приходящееся на единичную клетку бесконечно-малой области вблизи рассматриваемой точки), то закон сохранения тензора выражается инвариантным уравнением:

где Г^α_αβ — величины, определяющиеся выбором системы отсчета. Они выражаются через g_αβ, а именно:

Величины эти не имеют тензорного характера, т. е. всегда может быть выбрана такая система отсчёта, в которой все они равны нулю:

Эти величины определяют силы инерции и выражают собой кинематическое значение метрических соотношений. Уравнение (IV) и является основным законом сохранения энергии-материи. Эйнштейном было предположено, что тензор Т^α_σ должен так зависеть от g_αβ и производных, быть такой их функцией, чтобы уравнения (IV) были выполнены тождественно по подстановке в них выражения Т^α_σ через g_αβ

Эйнштейн показал, что такое выражение (V) действительно существует, а именно это — комбинация, стоящая слева в (II), обращающая уравнения (IV) по подстановке её вместо Т_αβ в тождество. На этом основании и были формулированы основные уравнения гравитационного поля. Тензор Т_αβ входящий в эти уравнения, определяет роль материи-энергии. Он называется, как уже упоминалось, тензором энергии-материи. Мы отметили уже, что характер зависимости этого тензора от g_αβ и х_α не может быть задан произвольно, а определяется решениями нелинейных уравнений Эйнштейна (IІ) — g_αβ (х₁, х₂ х₃, х₀), т. е. метрикой пространственно-временных соотношений,  которая, в свою очередь, определяется характером распределения и движения энергии в рассматриваемой области, т. е. тензором Т_αβ.

ОСНОВНЫЕ ПРИНЦИПЫ КВАНТОВОЙ ТЕОРИИ (Приложение к ст. «Энергия»).

Квантовая теория — современный этап в развитии атомизма, т. е. современная физическая теория, изучающая законы атомных процессов (микропроцессов). Основные принципы квантовой теории были установлены в 1925—1928 гг. в целом ряде работ как теоретических, так и экспериментальных. Этому предшествовал длительный период (1900—1925) накопления экспериментального материала и предварительных попыток его теоретического анализа. Из теоретических исследований особое значение имели работы Эйнштейна, Борна, Бора, Гейвенберга, Дирака, Шредингера, Л. де Бройля, Паули и мн. др. Экспериментальные исследования насчитываются тысячами. В настоящее время квантовая теория является ведущей дисциплиной всей теоретической физики, а ее принципы являются фундаментом для всякого исследования физических и химических микропроцессов.

Основной чертой квантовой теории, резко отличающей её от всех предыдущих физических теорий, является очень глубокая критика правомерности применения в атомном мире целого ряда самых основных физических понятий, как то: скорости, местоположения частицы, механического движения и т. д., т. е. таких физических понятий, которые, казалось, установлены были с исчерпывающей ясностью. Новая теория стремится определить сферу действия того или иного из основных физических понятий, т. е. определить те области явлений, в которых они правильно отображают действительность (атомный мир) и вне которых они перестают иметь силу, искажают действительность и нуждаются в изменении. При этом главное внимание обращается как раз на последние случаи, т. к. именно тогда обнаруживается неадекватность действительности старых физических понятий, и мы переходим в новую, квантовую область явлений.

Для правильного понимания квантовой теории в её современной форме, прежде всего, следует обратить внимание на то, что она пользуется исключительно старыми (называемыми классическими) понятиями, выработанными макроскопическим опытом, но использует их для формулировки новых, существенно выходящих за пределы этих понятий, физических закономерностей. Это достигается изменением связей, соотношений, «контекста», в котором употребляются старые понятия. Создаётся своеобразный новый язык, язык микрофизики (здесь уместна аналогия с понятием «идиоматических выражений» лингвистики), ставящий задачей отобразить возможно полнее и точнее вновь открытый микромир, до тех пор почти совершенно неизвестный экспериментально. Громадное значение при этом получает математический аппарат, т. е. количественная формулировка соотношений между различными характеристиками атомного процесса, не могущими быть выраженными целиком в терминах макроскопически определенных понятий и требующими поэтому существенно новых понятий, существенно новых формулировок закономерностей.

В развитии квантовой теории различимы два основных этапа:

I. Этап, связанный с критикой концепции механического движения, закончившийся выработкой понятия «квантовой частицы» (1900—1925).

II. Этап, связанный с переходом от механических проблем к проблемам электродинамическим. Этот период до настоящего времени еще не закончился, так как до сих пор электродинамические квантовые проблемы во многих отношениях не разрешены.

Исторически квантовая теория возникла из весьма многочисленных попыток дать последовательную теорию строения атома, основных свойств излучения и других атомных процессов, опираясь на механические принципы. Особое историческое значение из этих попыток имеют: 1. Представление о квантовом газе: фотонный газ (Эйнштейн, Бозе, Планк), попытки объяснения теплоёмкости (Дебай, Эйнштейн). 2. Теория строения атома Н. Бора, принципы которой были им найдены в 1912 г., причем им была использована электронная теория Г. А. Лоренца, имевшая вообще громадное значение в развитии квантовой теории. Целесообразно проследить изменение принципов, приведшее к квантовой теории, на этом примере.

В конце XIX века Г. А. Лоренцом была развита электронная теория (см. LIІ, 192 сл. ), дающая принципы механического движения (и излучения энергии электрически-заряженной частицы, подвергающейся воздействию внешних электромагнитных полей и являющейся, в свою очередь, источником электромагнитного поля). Эта теория в дальнейшем развилась в релятивистскую теорию поля. Она не учитывает атомизм действия, будучи т. о. классической, а не квантовой теорией. Далее теория Лоренца не дает анализа структуры электрически-заряженной частицы.

Экспериментальные исследования, осуществлённые в конце XIX и в начале XX вв., привели к следующим основным выводам:

1. Электрический заряд имеет атомную структуру (т. е. состоит из отдельных атомов электричества, т. н. элементарный электрический заряд, величина которого была измерена, в частности, Милликеном, см. LII, 194). Существуют атомы электричества положительные и отрицательные. Электрический заряд подчиняется закону сохранения.

2. Механическая, инертная масса имеет атомную структуру. Каждая отдельная индивидуальная частичка имеет вполне определенную массу, которую современная экспериментальная техника позволяет измерить с очень большой точностью. Масса микроскопической частицы m₀ является её энергетической характеристикой, а именно, если Е — энергия частицы, а р — её количество движения, импульс, то с этими величинами непосредственно связана инвариантная релятивистская характеристика частицы, а именно инвариант

являющийся мерой массы m₀ частицы (см. выше стб. 182). В системе отсчёта, в которой импульс частицы равен нулю, масса частицы   определяется её энергией покоя:

3. Отдельный атом состоит из ядра, несущего заряд +Z_е (Z — целое  число, равное числу протонов, входящих в состав ядра), и Z электронов, удерживаемых полем электростатического притяжения ядра (опыты Резерфорда, см. LIІ, 206 сл.).

Таким образом, было установлено, что отдельный атом представляет собой электродинамическую систему, свойства которой, казалось, возможно рассчитать, пользуясь теорией Лоренца. Такие расчёты и были выполнены (Шотт и др.). Однако они показали почти полную непригодность теории Лоренца для этой цели, так как по ней получалось, что уже после нескольких сот тысяч оборотов вокруг ядра электрон отдаст больше половины своей энергии в виде электромагнитного излучения и, таким образом, атом вообще не может, по теории, существовать как устойчивая система, тогда как мы внаем, что атомы существуют, не изменяясь в основных своих свойствах, миллиарды лет (спектры звезд, геологические исследования радиоактивных элементов и т. д.).

Таким образом, сущность расхождения между теорией Лоренца и свойствами реального атома заключается в следующем. По теории Лоренца, электродинамические реакции (свечение, возбуждение электромагнитного поля и т. п.) имеют величины того же порядка, что и реакции механические, и поэтому система из движущихся электрически-заряженных частиц неустойчива. Для реальных же атомов, хотя они и состоят из электрически-заряженных частиц, имеется иное положение вещей, а именно:

а) Атом существует стабильно, обладая совершенно определёнными энергетическими характеристиками (запасом энергии, моментом импульса и т. п.).

б) Электродинамические реакции атома (свечение и т. д.) имеют в энергетическом смысле (в смысле соответствующих величин энергии) характер «поправок», небольших изменений энергетических величин, присущих стационарному состоянию. Они непосредственно связаны лишь с нарушением стабильности атома, т. е. с переходом атома из одного стационарного состояния в другое, и отсутствуют в стационарном состоянии.

Таким образом, с точки зрения эксперимента, для атома, как электродинамической системы, характерно, во-первых, существование стационарных, состояний и, во-вторых, существование переходов, связанных с электродинамическими реакциями, вызывающих сравнительно малые изменения энергетического режима в  атоме. В этом направлении и должна была быть изменена электродинамика Лоренца. Дальнейшие исследования выяснили, что значения энергии при электродинамических реакциях, получающиеся по расчёту, сделанному согласно принципам теорий Лоренца, определяются двумя различными обстоятельствами, а именно: 1) дискретностью количества энергии, теряемой или поглощаемой атомом в индивидуальном акте перехода, и 2) вероятностью реализации этого отдельного акта перехода. Классическая теория не выделяла последнее обстоятельство особо, а рассматривала процесс так, как если бы речь шла  об индивидуальном процессе с непрерывным изменением энергии в количестве, определяемом обоими указанными обстоятельствами. Анализируя строение   атома, Н. Бор и внес в теорию Лоренца поправки, соответствующие учету двух отмеченных выше свойств реальных электродинамических систем (атомов). Однако при этом он сделал естественное в то время допущение, что поведение составных частей атома в стационарном состоянии может быть полностью описано посредством механических принципов.

Теория Н. Бора известна под названием «старой квантовой теории». В длинном ряде работ, появившихся за период 1912—1925 гг. (см. XLI, ч. 4, 70/76 и LII, 199 сл.), были весьма детально прослежены самые разнообразные практические следствия старой квантовой теории. Так, например, был осуществлён расчёт энергетической структуры водородного, гелиевого и некоторых других атомов. Исследовано возмущающее действие электрического и магнитного полей на движение связанного электрона. Исследовались основные свойства молекул (теории инфракрасных спектров), исследовались, наконец, многие электрические и магнитные свойства вещества. В большинстве случаев сравнение результатов теории Бора с опытом показало, что имеется резкое, принципиальное расхождение не только количественное, но и качественное (примеры: существование орто- и парагелия, аномальный эффект Зеемана, электропроводность, статистика фотонов, значение моментов импульса атомов и молекул и т. п.). Выяснилось, что теория, будучи во многих отношениях безусловно верной, все же в чем-то основном качественно неправильна, что обусловлено какими-то неизвестными, новыми чертами, имеющимися в микромире по сравнению с макроскопическими закономерностями. В настоящее время мы знаем, что это расхождение обусловлено тем, что старая теория неправильно учитывала атомизм действия. Теория Бора являлась, в сущности, необоснованной вполне проекцией макроскопических свойств в атомный мир. Выяснение этого обстоятельства и означало переход к квантовой теории.

Анализ расхождений теории Бора с опытом показал, что несоответствие коренится в допущении, что стационарное состояние может быть описано чисто механически, т. е. как движение частиц (электронов), «пойманных» силовым полем ядра (кулоновское электростатическое притяжение) по законам классической механики. Соответственно этому наметились две возможности уточнения или модификации теории:

а) Сохраняя в основном концепцию о частицах, движущихся вокруг ядра, попробовать изменить силовой закон поля ядра. Мыслимо допустить, что на самом деле имеет место не кулоновский закон взаимодействия зарядов, а какой-либо другой (например, изменение взаимодействия заряженных частиц в атоме происходит очень быстро во времени и т. д.) и, таким образом, имеют место другие энергетические соотношения; при этом электроны в атоме имеют иные орбиты, чем в кулоновом поле.

б) Отказ от понятия частицы и ее механического движения в применении к электронам в атоме: представление атома как чего-то целостного, в смысле теории непрерывного физического поля.

Многочисленные попытки осуществить вариант (а) показали, что он совершенно непригоден и дает резкое отличие от опыта; таким образом, эта возможность отпала. Вариант (б), со своей стороны, наталкивается на целый ряд весьма существенных затруднений, преодоление которых и являлось переходом к квантовой теории. Отметим важнейшие из этих затруднений. Отказ от понятия частицы, движущейся по определённой траектории, можно, прежде всего; мыслить себе как переход к представлению о «размытой частице», точнее, к полю, ее заменяющему, занимающему всю область атома или какую-то его часть, более или менее обширную. Такое представление об электроне, как об облаке электрической «жидкости», уже было использовано в начале XX в. в примитивной форме в флюидной теории атома (Дж. Томсона, ср. LII, 198/199). Однако эта теория была отброшена после опытов, установивших следующие основные свойства атомных частиц.

Имеют место и могут быть непосредственно демонстрированы (в камере  Уильсона, см. XXXV, 336) индивидуальные акты столкновений частиц, происходящие в точном согласии с законом сохранения энергии и импульса. К этой группе опытов, прежде всего, относятся опыты Комптона, Комптона и Симона, Боте и Гейгера с рассеянием света электронами. В этих опытах могут быть прослежены баланс энергии и импульса для отдельного акта столкновения. Опыт показывает, во-первых, существование таких актов и, во-вторых, что они проходят с выполнением  классических законов сохранения энергии и импульса.

К этим же непосредственным доказательствам существования индивидуальных квантовых процессов следует отнести и все опыты с возбуждением и ионизацией атомов, подтверждающие известные соотношения, установленные Н. Бором, т. е. существование стационарных состояний у атомов и переходов их из одного стационарного состояния в другое. Таковы опыты Франка—Гертца, имевшие очень большое значение.

«Пустота» внутриатомного пространства для быстрых частиц, т. е. чрезвычайно редкое число столкновений частиц потока, пронизывающего атом, с составными частями последнего: ядром и электронами. Исторически именно эти свойства атомов и определили «планетарную» модель атома, явившуюся исходной при развитии теоретических представлений атомной физики.

Все перечисленные обстоятельства являются частными выражениями следующего основного факта: с энергетической точки зрения структура частицы (электрона, ядра) характеризуется значением энергии порядка m₀с², тогда как связанность частиц в атоме характеризуется значениями энергии порядка ионизационных потенциалов, т. е. в тысячи и сотни раз меньшими. Это значит, что всякая возможность заменить электрон или ядро облаком попросту отпадает, и не может быть никакой речи о том, чтобы рассматривать проблему энергетической связанности частиц в атоме и проблему связанности составных частей электрона в целое в одной плоскости.

В самом деле, допустим, что имеется электрон, являющийся волновым образованием — «волновым пакетом». Внесем в сферу его действия протон, приблизив последний на расстояние около 10^-8 см к электрону. Мы получим водородный атом в стационарном состоянии. Это значит, что волновая картина должна быть заменена картиной стоячих колебаний, гармонических колебаний. Но это не что иное, как утверждение о том, что электрон «размазался». Мы получим, таким образом, затратой энергии в несколько вольт возможность «размазать» электрон, на что требуется энергия порядка m₀с². Это показывает нелепость интерпретации квантовой «волновой» природы электрона в буквальном смысле, т. е. нелепость представления электрона или другой частицы в виде волнового образования (пакета) из  ψ-волн (см. об этом далее).

Таким образом, возникла чрезвычайно трудная задача: выработать в соответствии со  всей совокупностью атомных опытов такое представление об атомной частице, в котором: 1) сохранилось бы правильное соотношение, в энергетическом смысле, между структурой частицы и связью частиц в стабильную систему и имели бы место законы индивидуальных процессов столкновений, упоминавшиеся выше, 2) было бы совершенно переработано понятие механического движения; при этом изменению должны подвергнуться кинематические представления. На первый взгляд эта задача невыполнима и внутренне противоречива. Однако развитие физики показывает, что именно на этом пути находилось правильное разрешение затруднений теории атомных процессов и что именно таким путем достигается более точное воспроизведение атомной теорией основных свойств реальных атомных процессов.

Существенно новым элементом, который позволяет осуществить описание индивидуальных атомных процессов средствами классической теории, — учитывая отличие их от классических, — является статистический характер соотношений. Не следует представлять себе дело так, как если бы переход к квантовой теории означал переход к такой статистической теории, в которой нет места для индивидуальных, не статистических закономерностей. Наоборот, квантовая теория имеет дело с индивидуальными процессами, но такими, которые могут быть описаны классически лишь при статистическом способе употребления классических понятий, служащих для их описания. В этом её глубокое отличие от всех других статистических теорий. Рассмотрим более подробно это отличие и вместе с тем рассмотрим метод употребления классических понятий при описании реальных атомных процессов.

Статистический ансамбль. Предположим, что изучается некоторый объект, поставленный в определённые условия (примеры: электрон, проходящий через дифракционную решетку, или из совсем другой области: бросание игральной кости — последний пример часто употребляется в теории вероятностей). Рассматривая этот объект статистически, мы образуем из очень большого числа независимых друг от друга экземпляров этого объекта статистический ансамбль. Мы можем, например, брать всё новые и новые экземпляры данного объекта, ставя его в те же условия испытания*.

*) Здесь имеет место очень глубокая проблема современной теории вероятностей: определение условий равновероятности событий. Но её мы здесь не затрагиваем.

В результате статистического испытания нашего ансамбля мы получим некоторое распределение N испытанных экземпляров по различным возможным значениям какого-либо признака  α (например, распределение брошенных костей по выпавшим очкам):

Пусть число экземпляров объекта, для которых получено, что α=α_k обозначается через N_k.  Тогда для достаточно большого числа испытаний значения N_k:N (N число испытаний) определяет вероятность w(α_k) того, что для (N+1)-го экземпляра получится значение признака α=α_k. Статистический ансамбль может исследоваться, таким образом, по самым разнообразным признакам объекта. Если окажется, что w(α_k) = і для одного какого-либо значения α=α_k и, следовательно, w (αj) = 0 для всех-остальных значений αl ≠ α_k, то это значит, что исследуемый ансамбль однороден по признаку α. Характеристикой однородности ансамбля по какому-либо признаку k служит равенство нуля средней квадратичной ошибки для признака k:

Это условие может быть написано так же, как равенство квадрата среднего среднему квадрата, т. е. как

Для величин, по которым ансамбль не однороден, средние квадратичные ошибки _ΔL, _ΔM, _ΔN... и т. д. отличны от нуля.

В этих случаях ансамбль характеризуется средними значениями данных величин. Если величина А имеет возможные значения (і), причём в список (1) входят все возможные значения А, и каждое из этих значений имеет вероятности:

то среднее значение величины А равно*

Условия, в которые ставится исследуемый объект и которые определяют, следовательно, ансамбль в целом, можно, вообще говоря, характеризовать тем, что некоторые величины β имеют для каждого экземпляра, входящего в ансамбль, одно и то же фиксированное значение: β = β_k. Мы должны, поэтому, строго говоря, вместо ω(α_k) писать ω_βk(α_k), указывая при символе вероятности, что берётся вероятность именно при β = β_k, а не какая-либо иная.

*) Если величина А имеет непрерывную область значений, то сумму в (5) должно понимать как интеграл Стильтьеса.

Квантовые и классические ансамбли. Для статистических ансамблей существуют свойства, которые общи всем им и которые выражают, следовательно, основные статистические закономерности. Именно в этих свойствах и имеют место отличия между классическими статистическими ансамблями, с которыми всегда имело дело исчисление вероятностей, и квантовыми ансамблями, с которыми впервые столкнулась атомная экспериментальная физика. Таким образом, квантовые ансамбли были сначала обнаружены в реальном атомном мире и лишь затем была разработана их математическая теория, которая и есть не что иное, как квантовая теория.

В атомных экспериментах отличие между ансамблем, образованным из квантовых процессов, и ансамблями, изучавшимися до сих пор исчислением вероятностей, особенно отчётливо обнаруживается в том, что тогда как для обыкновенных ансамблей основные свойства вероятностей (теоремы сложения и умножения) применимы во всех случаях без исключений, для квантовых ансамблей существуют случаи, когда непосредственное применение этих теорем оказывается иллюзорным, т. е. не выражает должным образом объективные свойства реального атомного ансамбля. Рассмотрим типичный пример, взяв его в должной общности (далее мы дадим конкретные примеры).

Пусть дан ансамбль, определённый условиями достоверности некоторого квантового события, которое назовем А, и пусть для ансамбля определяется вероятность события С (скажем, что некоторая величина С имеет одно из своих возможных значений σ_k). Обозначим эту вероятность через ω_A(С). Пусть, далее, имеется серия альтернативных, т. е. исключающих друг друга, событий, которые мы обозначим:

причём, в этот список пусть входят   все альтернативные события по данному признаку. (Мы можем, не ограничивая общности, допустить, что события В состоят в том, что некоторая величина В имеет то или иное из своих возможных значений β₁, β₂,…, β_k).

Пусть вероятность события В_k для нашего ансамбля (определённого тем, что реализовано событие А) обозначается

Пусть далее (С) есть вероятность события С при условии реализации события, В_k. Тогда известная теорема умножения вероятностей (см. ХLI, ч. 7 329, 329/30) гласит, что между ω_Вk (С), ω_A (В_k) и ω_A(С) всегда существует соотношение:

т. е.: вероятность события С при достоверности событий А и B_k равна произведению вероятности события B_k при достоверности события А на вероятность события С при достоверности события B_k. Пользуясь этой формулой, мы всегда можем вычислить вероятности ω_A(С), т. е. вероятность события С при достоверности события А. Для этого мы должны воспользоваться теоремой сложения вероятностей (см. XLI, ч. 7, 329), имеющей место для альтернативных событий, а именно мы должны просуммировать выражение (7) по всем возможным, альтернативным событиям (6), Тогда сумма  

при суммировании по всем возможным В_k равна вероятности осуществления события С при достоверности события А и при достоверности осуществления какого-либо (безразлично какого) события из серии альтернативных событий (6). Таким образом,

Какие-либо специальные предположения относительно А, В_k, С при этом не делаются, — за исключением одного, всегда молчаливо допускавшегося в исчислении вероятностей и как раз оказавшегося неправильным для квантовых ансамблей. Для последних применение формулы (8) во многих случаях*, как показывает непосредственная практическая проверка на атомных опытах, ведёт к неверным количественным подсчётам и таким образом (8) не отражает свойства реальных атомных статистических ансамблей. Это явление получило специальное название ещё до выяснения его  смысла — когерентность. Анализ расхождения между (8) и опытом показывает, что дело здесь в том, что для квантовых ансамблей сделанное в (7) предположение о принципиальной возможности, реализации ансамбля, для которого были бы совместно достоверными события А и В_k, неверно, недопустимо физически, т. е. таких ансамблей объективно не существует. Иначе говоря, в формуле (7) левая часть, относящаяся к  ансамблю, определённому заданием как А, и В_k, относится к воображаемому, несуществующему физически ансамблю, тогда как в правой части перемножаются величины W_A (В_k) и W_Bk (С), относящиеся к совершенно различным ансамблям, почему их произведение и не имеет никакого объективного значения. Соответственно этому, теряет силу и весь дальнейший вывод, приводящий к формуле (8), которая, как сказано, не всегда справедлива. Таким образом, мы приходим к выводу: если события А и В_k таковы, что нет ансамбля, для которого А и В_k, совместно могут рассматриваться как реализованные и входящие в его характеристику (задание условий, определяющих ансамбль), то тогда (7) и (8) не имеют места, и мы имеем дело с квантовыми событиями; если же события А и В_k таковы, что  имеется ансамбль, для которого А и В_k совместно могут рассматриваться как реализованные и входящие в его характеристику, то тогда (7) и (8) имеют место и, как показывает опыт, справедливы все классические законы, все классические соотношения между А и В_k.

^*) А именно в тех и только тех случаях, когда классические соотношения оказываются неверными. Если (8) имеет место, то в этих случаях нет никакого различия между классической и квантовой теориями. Классические соотношения сохраняются в этих случаях без изменений.

Таким образом, сущность квантовой модификации сводится к указанным особенностям, и мы должны рассмотреть их более подробно. Мы можем формулировать различие между квантовым (когерентным) и классическим, обыкновенным ансамблем еще в следующей форме. Пусть дан классический ансамбль, в котором имеется признак α, по которому осуществлено распределение. Отбирая из ансамбля все экземпляры с α = α', составляя из них новый и относя все остальные в другой ансамбль, мы можем представить данный, исходный ансамбль, как смешение этих двух. Последние будут различными ансамблями (в одном только α = α', в другом нет α ≠ α'). Для всякого классического ансамбля принципиально возможно представить его смешением двух различных ансамблей. Квантовый же (когерентный) ансамбль обладает той особенностью, что он не расчленим в том смысле, что все могущие быть образованными из него под ансамбли, дающие по своём смещении исходный ансамбль, идентичны по своим свойствам с последним. Это свойство особенно ясно выявляет отличие квантового ансамбля от классического, необходимость изменений в исчислении вероятностей. Изменения эти, будучи на первый взгляд весьма частными, являются величайшим изменением всей схемы исчисления вероятностей, так как они означают, что для квантовых ансамблей заново должны быть рассмотрены все основные задачи исчисления вероятностей.

В самом деле, в исчислении вероятностей применительно к квантовым ансамблям должна быть отображена невозможность ансамбля, задаваемого квантово-несовместными событиями, т. е. событиями, которые не могут фигурировать совместно в качестве признаков, определяющих ансамбль. В то время как для классических ансамблей несовместными являются лишь такие свойства, которые логически несовместны, в смысле закона исключенного третьего, для квантовых ансамблей, кроме такой несовместимости, в смысле логического отрицания, существует еще несовместность в совершенно новом смысле (квантовая несовместность), а именно в том смысле, что нет ансамблей, для которых бы совместно реализовались в качестве условий, его определяющих, два квантово несовместных события (в нашем примере это А и В_k). Фундаментальное отличие между квантовым и классическим ансамблем может быть формулировано еще следующим образом. Допустим, что рассматриваемые в (6), (7), (8) события заключаются в том, что некоторые физические величины А, В, С получают одно из  своих возможных значений. Тогда условие реализации события можно записать как условие, что для рассматриваемого ансамбля все входящие в него экземпляры имеют одно и то же значение данной величины, и, следовательно, ее квадратичная ошибка равна нулю. Таким образом, в формуле (7) слева стоит величина, относящаяся к ансамблю, для которого средние квадратичные ошибки (флюктуации, меры рассеяния) величин А и В равны нулю:

Справа стоят величины, относящиеся к разным ансамблям, для которых:

W_A (B_k) задано при ΔА = 0 и W_Bk (С)  задано при ΔВ = 0 соответственно.

Непригодность формулы (8) означает, что нет ансамбля, для которого совместно выполнялись бы условия реализации А и В, т. е. условия (9). В этом и только в этом случае формула (8) становится иллюзорной, так как W_A (B_k) и W_Bk (С)  относятся к существенно разным ансамблям.

Таким образом, для атомных ансамблей имеют место два случая:

1. Физические величины А и В таковы, что принципиально существует статистический ансамбль, для которого совместно выполнены условия (9),  т. е.

В этом случае нет никакого отличия от соотношений, изучаемых классической теорией. Соотношения между А и В, даваемые последней, остаются справедливыми и для квантового объекта.

2. Величины А и В таковы, что не существует ансамбля, для которого совместно выполнялись бы условия (9), (9’). В этом случае, и только в этом, соотношения между А и В, даваемые классической теорией, отпадают и имеют место существенные отличия атомных явлений от тех, которые изучаются классической теорией. Это и есть количественная формулировка атомизма действия, обусловливающего неустранимое, т. е. объективное, физическое квантовое рассеяние. Ансамбль с ΔА = 0 будет в этом случае обязательно иметь ΔВ ≠ 0 и, обратно, ансамбль с ΔВ = 0 имеет ΔА ≠ 0. Задача квантовой теории и заключается в исследовании законов этой корреляции в качестве характеристик индивидуальных атомных процессов. Приведем два важнейших примера.

1. Прохождение частицы через потенциальный барьер. Как известно, согласно законам классической механики, частица, пойманная силовым полем, может уйти из него в бесконечность лишь в том случае, если она получит энергию, превышающую ее энергию связи данным силовым полем. Пусть по оси абсцисс (см. рис.) отложены значения радиуса вектора r, по оси ординат — значения энергии частицы в силовом поле, определяемом потенциалом u (r). Если частица имеет энергию E₀, то она поймана силовым полем и может совершать движения лишь до значения r₀, при котором Е₀ = u (r₀),  и затем возвращается назад, так как при r > r₀, Е₀ < u (r) и скорость частицы была бы мнимой. Если энергия частицы больше энергии связи,   например, Е = Е₁, то частица может беспрепятственно уйти в бесконечность. Экспериментальные исследования радиоактивности, вырывания электронов электрическим полем из холодного металла, далее, некоторых химических явлений и т. п. показали, однако, что α-частицы, электроны и другие атомные частицы могут беспрепятственно покидать силовое поле; частицы как бы «просачиваются» сквозь барьер, имея после прохождения «барьера»   энергию Е₀, меньшую энергии связи («туннельный эффект»). Мы имеем здесь дело с одним из важнейших случаев непригодности классических концепций для описания индивидуального атомного процесса. В самом деле, если мы сохраним концепцию частицы, то мы должны допустить для нее возможность мнимой скорости, когда она проходит под барьером, что нелепо. С другой стороны, если мы допустим, что она приобретает энергию, достаточную для перевала через барьер, а затем её теряет, то это будет полным отказом от закона сохранения энергии, что также нелепо*. Таким образом, индивидуальный процесс прохождения частицы через барьер не может быть формулирован посредством классического представления о частице, движущейся по определенной механической траектории. Допущение, что вместо частицы мы имеем дело с размазанным волновым «пакетом», её заменяющим (Шредингер в 1926 г.), т. е. допущение, что когда частица движется внутри или вне поля, она является «собранной волной», а когда она проходит под барьером, то она расчленяется на отдельные парциальные волны, также в корне противоречит закону сохранения энергии, так как тогда в этом процессе должны были бы участвовать энергии порядка m₀c², что, как доказывает опыт, на самом деле не имеет места.

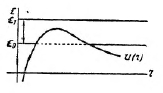
Рис. 1

Квантовая теория описывает прохождение частицы через потенциальный барьер, пользуясь классическими понятиями, а именно, употребляя их применительно к статистическому ансамблю. В данном случае задача ставится следующим образом. Прежде всего, образуется статистический ансамбль из бесконечно большого числа индивидуальных прохождений одинакового типа, т. е. с одинаковым типом u(r). Этот ансамбль и будет примером квантового ансамбля, так как энергия частицы Е и ее местоположение (координата r) как раз являются величинами, находящимися в выше формулированном соотношении друг с другом: не существует ансамбля, для которого совместно имели бы место условия

Ансамбль с Δr=0 имеет неизбежно ΔЕ ≠ 0 и, обратно, с ΔЕ=0 имеет Δг≠0. Если бы существовал ансамбль, для которого совместно выполнены условия (10), то тогда прохождение частицы через барьер было бы невозможно, ибо имели бы место классические законы. Невозможность такого ансамбля указывает на невозможность описать этот индивидуальный процесс классически. Ансамбль же из таких процессов может быть описан в классических понятиях как ансамбль, обладающий определённой корреляцией между ΔЕ и Δr. А именно, если мы возьмем ансамбль, объединённый из индивидуальных прохождений, в которых частицы имеют определённое начальное значение энергии Е₀, так что ΔЕ = 0, то этот ансамбль будет иметь определённое рассеяние частиц по их местоположениям, определяемое флюктуацией Δr, которая и может быть вычислена по методам квантовой теории. Распределение частиц по r может быть, таким образом, вычислено для этого ансамбля, равно как и соответствующие вероятности, характеризующие ансамбль. Обратно, взяв ансамбль с Δr=0, мы можем получить количественную характеристику процессов, вычислив распределение частиц по значениям энергии Е и вероятности реализации того или иного значения Е.

^*) То же самое можно сказать о допущении, что силовое поле u(r) испытывает быстрые изменения, и что частица проходит, когда u(r) понижается. Это также в корне противоречит закону сохранения энергии.

Этим путём были подтверждены теоретически основные количественные характеристики туннельного эффекта, полученные экспериментально. Например, так был объяснен эмпирически установленный закон радиоактивности Гейгера—Неттола.

Современная теория электропроводности в значительной мере основана на квантовой теории туннельного эффекта. Квантовое обоснование теории электропроводности развито было в 1928—1930 гг. в целом ряде работ. Большое значение имеет туннельный эффект в явлениях химической кинетики и катализа, а также в вопросах строения молекул.

2. Дуализм волн и частиц. Другим примером отличий квантового ансамбля от классического может служить явление дифракции потока независимых частиц, идущих последовательно друг за другом черев дифракционный прибор (см. XXXVII, 558/62). Рассмотрим простейший случай, несколько схематизируя соотношения для того, чтобы с большей ясностью выступили отличия квантовых ансамблей от классических. Пусть дифракционный прибор состоит из двух щелей, на которые падают частицы, имеющие почти одно и то же начальное значение вектора импульса. Сравним поведение потока классических частиц (дробинки) и частиц квантовых. Рассмотрим сначала классический случай. Пусть опыт осуществляется в двух следующих вариантах.

А. Оба отверстия открыты, и за дифракционным прибором поставлен экран, на котором отмечаются попадания частиц (фиксируется точка, в которую она попала).

В. Около прибора имеется наблюдатель, остающийся нам неизвестным, который следит за частицами, подходящими к прибору, и, видя частицу, подходящую к одной из щелей, закрывает другую, т. е. ту, через которую частица не проходит.

В классическом случае, очевидно, этот процесс закрывания щели, черев которую не проходит частица, ничем не может повлиять на частицу, проходящую черев другую щель, и результат обоих опытов А и В будет одинаковым: распределение точек попаданий частиц на экране будет одинаковым, и наблюдатель, закрывавший щель, нам останется неизвестным.

Совсем другое получается для квантового ансамбля, т. е. для серии независимых прохождений через дифракционный прибор квантовых частиц. Пусть в этом случае также осуществляются два варианта опыта:

А. Оба отверстия открыты, и за дифракционным прибором поставлен экран, на котором отмечаются попадания частиц (фиксируется точка, в которую она попала).

В. Производится серия опытов — прохождений отдельных частиц через дифракционный прибор с закрыванием то одной, то другой щели. Результаты этих опытов, т. е. точки попаданий частицы на экран, перечерчиваются на одну сводную таблицу (изображение экрана).

Вариант (В) является тогда аналогом варианта (В) в вышеприведённом классическом случае. Опыт показывает, что в отличие от классического случая между обоими вариантами в квантовом случае имеется резкое отличие: в случае (А) имеет место, так называемое когерентное дифракционное распределение от двух щелей, в случае (В) получается два независимых, некогерентных друг с другом, дифракционных распределения. Попадания частиц на экран будут распределены вполне определённым образом. В случае одной щели распределение, при очень большом числе частиц, прошедших через щели, будет иметь характер распределения интенсивности дифрагировавших волн; мы получим светлое пятно и дифракционные картины от краев щели. В случае двух щелей распределение будет таким, как если бы оно создавалось интерференцией волн, прошедших через обе щели; будут иметься максимумы и минимумы попаданий частиц, вполне соответствующие интерференционной картине. Когда же речь идет о попадании одной квантовой частицы, то она всегда дает «точечное» воздействие, т. е. попадает во вполне определённое место экрана.

Характер распределения частиц, выявляющий все черты интерференционной картины, привел к представлению о волнах, сопровождающих эти частицы и как бы направляющих их движения (теория «волны-пилота» Де-Бройля и энергии Шредингера). Однако такая концепция находится в противоречии с упоминавшимися выше основными свойствами квантовых ансамблей (нерасчлененность) и, таким образом, физически неправильна. В самом деле, если бы эта теория была верной, то тогда, принципиально было бы возможно рассматривать ансамбль прохождений частиц через щель как классический, а это означало бы невозможность интерференционных явлений.

Необходимость изменения представления о механическом движении частицы иногда выражают термином «дуализм волн-частиц», однако надо заметить, что этот термин может быть осмыслен только после того, как дано представление об особенностях квантовых ансамблей. В противном случае он может повести к неверным представлениям о квантовых процессах как имеющих две стороны — волновую и корпускулярную, чего на самом деле нет. Действительно волновые свойства, т. е. интерференционная картина, реализуется только как свойство ансамбля квантовых отдельных процессов, например, процессов прохождения отдельного электрона через дифракционный барьер, вылета α-частицы из ядра и т. д. Корпускулярные же свойства являются, в сущности, выражением законов сохранения энергии и импульса для отдельного элементарного квантового процесса: отдельное попадание электрона в ту или иную точку экрана, отдельный акт столкновения (опыты Комптона—Симона, Боте и Гейгера и т. п.).

Для анализа связи волновых свойств и корпускулярных существенно усмотреть, что в первых выражается свойство квантового ансамбля, а именно его нерасчленённость на различные подансамбли, и что, таким образом, статистические закономерности имеют для волновых свойств основное значение.

Таким образом, для квантового ансамбля закрывание щели, через которую не проходит частица (если пользоваться классическим языком), существенно влияет на результат опыта, так как этот процесс, который, казалось бы, не имеет никакого значения, уничтожает возможность создания определённой картины распределения попаданий частиц на экран. Это значит, что понятие о частице, движущейся по определенной траектории, т. е. классическая   концепция механического движения, не соответствует действительности, т. е. квантовый индивидуальный процесс прохождения атомной частицы через дифракционный прибор существенным образом отличен от этой концепции. Ситуация в этом случае, следовательно, аналогична рассмотренному ранее случаю прохождения частицы через силовой барьер и должна быть рассмотрена аналогичным образом. Квантовая теория этого процесса заключается в формулировке свойств ансамбля, образованного из серии независимых индивидуальных прохождений. Ансамбль характеризуется тем, что частицы начально имеют определенное значение вектора импульса р и, таким образом, флюктуация Δр может считаться равной нулю. Если бы имелась возможность классического описания процесса (как это имеет место в случае дробинок), то отбором частиц можно было бы выделить из данного ансамбля подансамбль, характеризуемый как прежним условием Δр≈0 так и условием Δр≈0. Отличие ансамбля от классического описания показывает, что эти условия несовместны и, таким образом, распределение частиц, получающееся в результате на экране, является выражением квантового рассеяния и описывается квантовой флюктуацией Δr. Характер распределения, законы его, т. е. полная характеристика рассматриваемого ансамбля, и в этом случае, так же как и в предыдущем примере прохождения частиц через силовой барьер, может быть установлена, если нам будут известны общие свойства квантового ансамбля, которые имеются у него вместо классических свойств, изучавшихся и установленных при допущении принципиальной возможности образовать подансамбль с нулевым рассеянием любых двух величин, описывающих ансамбль.

Литература: Планк М., «Принцип сохранения энергии», пер. с 4 нем. изд., М. — Л., 1938; Абрагам-Беккер, «Теория электричества», пер. с нем., 2 изд. [т. I], Л. — М., 1939; Беккер Р., «Электронная теория», пер. с нем., Л. — М., 1936; Дирак П. А. М., «Основы квантовой механики», пер. с англ., 2 изд., М. — Л., 1937; Weyl Н., «Gruppentheorie und Quantenmechanik», 2 Aufl, Lpz., 1931; Pauli W., «Quantenmechanik», в кн.: «Handbuch der Physik», Bd XXIV, 2 Aufl., В., 1933; Neumann J. von, «Mathematische Grundlagen der Quantenmechanik», В., 1932. Теория гравитации и понятие энергии электромагнитного поля: Einstein А., Grommet J. [статъи в] «Sitzungsberichte der Preussischen Akademie der Wissenschaften», Jahrg. 1927. Physikmathemat.-Klasse. В., 1927; Darmois G., «Les équations de la gravitation einsteinienne», Р., 1927; Hilbert D., «Gesammelte Abhandlungen», Bd_III, В., 1935.

К. Никольский.