Энтропия

Энтропия. Если какое-либо вещество, находящееся под равномерным давлением, расширяется изотермически при постоянной температуре t₁°C, а затем без притока и убыли тепла расширяется адиабатно, то вещество при этом последнем процессе охладится до некоторой температуры t₂°C. Если затем вещество будет изотермически сжато при температуре t₂°C, а вслед затем в  подходящий момент будет сжато адиабатно, то оно нагреется и достигнет начальной температуры t₁°C и начального давления и объёма. В результате вещество, отправившись из определённого состояния, вернётся в него же обратно, выполнив цикл своих изменений состояний (т. н. цикл Карно, см.) и совершив при этом некоторую работу А; при этом вещество заимствует из резервуара температуры t₁°C (нагреватель) количество теплоты Q₁ и отдаёт в резервуар температуры t₂°C (холодильник) количество теплоты Q₂, а разницу Q₁—Q₂ превращает в механическую работу, так что где

есть так называемый механический эквивалент теплоты (см. XLI, ч. 7, 487 сл.). Если все изменения состояния совершаются бесконечно медленно, то весь процесс может быть выполнен безразлично как в одном, так и в другом, прямо противоположном, направлении: он обратим.

Беря такой цикл достаточно малым (при данных t₁ и t₂) и повторяя его N раз, мы можем получить за счёт теплоты любое количество работы А = NJ (Q₁—Q₂). Беря иное вещество при тех же резервуарах t₁ и t₂ мы получим работу а для одного цикла, и, повторяя процесс n раз, всегда сможем получить работу

комбинируя теперь первый цикл со вторым, выполняемым в обратном направлении, мы в результате никакой работы не получим, и оба вещества после совершения циклов останутся в начальном состоянии; следовательно, по т. н. второму закону механической теории тепла (см. XLIII, 319/21) теплота могла только уйти с тела более тёплого (t₁) на более холодное (t₂). Если q₁ есть количество теплоты, перешедшее во втором цикле в нагреватель, то количество тепла, потерянное нагревателем, будет положительно, т. е.

Но весь этот процесс мы могли бы проделать и в обратном порядке: тогда по тому же второму закону будет

Оба условия требуют таким образом, чтобы

так как у нас

то, деля второе уравнение на первое, получаем:

Это отношение называется коэффициентом полезного действия, и мы видим, что он не зависит от вещества, и, стало быть, зависит только от температур резервуаров t₁ и t₂, т. е.:

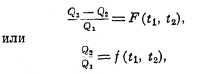
где F(t₁ и t₂) и f(t₁ и t₂) означает некоторую функцию температур t₁ и t₂.

Это возможно только в том случае, если будет

где φ означает некоторую функцию температуры t. Мы можем, положив φ (t)=T считать это Т само температурой. Тогда будет

и если выбрать скалу Т так, чтобы разница между значениями Т для температуры кипения воды и таяния льда равнялась 100, то оказывается, что Т есть как раз та самая абсолютная температура, которая в учении о теплоте появляется как следствие рассмотрения свойств идеальных газов и нуль которой есть —273° С. Это есть так называемая термодинамическая шкала температур Томсона.

Таким образом, у нас получается для рассматриваемого цикла соотношение

Но каково бы ни было изменение состояния вещества в некотором произвольном цикле, его всегда можно представить себе состоящим из бесконечно малых то изотермических, то адиабатных частей; если dQ есть количество теплоты, сообщаемое веществу в данном элементе цикла при температуре Т, то для всего цикла в общем случае вместо только что полученного выражения мы получим:

для замкнутого обратимого цикла. Это значит, что существует такая функция состояния вещества S, что

Эта функция S введена в науку Клаузиусом и названа им энтропией.

Из полученного соотношения легко найти энтропию, например, для идеального газа. По первому закону механической теории теплоты (см. XLI, ч. 7, 488)

где А есть работа внешних сил. Если газ находится под давлением р и его объём V, то работа внешних сил есть

с другой стороны, энергия идеального газа есть (для грамма вещества)

здесь С_v есть удельная теплота при постоянном объёме (см. теплоёмкость). Отсюда

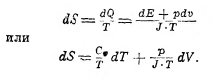
По свойствам идеального газа для одного грамма будет иметь место соотношение (см. XLI, ч. 7, 491):

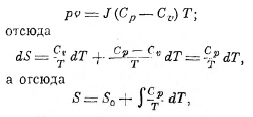
где S₀ есть энтропия идеального газа при абсолютном нуле температуры^*).

Мы рассматривали цикл обратимый; если он необратим, если, например, количество теплоты q зря,  так сказать,  взято из нагревателя и перешло в холодильник, так что из нагревателя взято всего

а отдано в холодильник

то в этом цикле коэффициент полезного действия будет

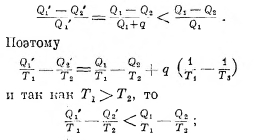
а так как правая часть этого выражения равна нулю, то имеем для необратимого цикла

^*) До работ Нернста, которыми была установлена т. н. «теорема Нернста», или третье начало термодинамики (см. XLI, ч, 7, 508), S₀, т. е. энтропия при абсолютном нуле, ничем далее не определялась. Теперь постоянная S₀ определяется из теоремы Нернста, значит в этом случае коэффициент полезного действия меньше, чем в случае обратимого цикла.

В общем случае для необратимого произвольного цикла имеем

здесь мы считали dQ > 0, когда оно берётся из резервуара; если считать наоборот dQ > 0, когда оно отдаётся в резервуар, то получим

это значит, что энтропия всех участвующих в процессе тел возрастает, если процесс необратим; так что энтропия является мерой необратимости процесса. При обратимом цикле она не меняется.

Выше выведенное выражение S относится к устойчивому состоянию термодинамического равновесия вещества (общее говоря, — физической системы; у нас — идеальный газ); но можно говорить и об энтропии в ином, неустойчивом состоянии, когда энтропии меньше. Естественным путём сама по себе всякая система переходит всегда из неустойчивого состояния в устойчивое; этот переход необратим, и энтропия системы при этом возрастёт, стремясь к максимуму при равновесии. Чем состояние ближе к устойчивому равновесию, тем меньше его необратимость, так что энтропия является и мерой устойчивости состояния; это обстоятельство устанавливает возможность выражения энтропии и иначе, при помощи теории вероятностей (см.). Дело в том, что понятие об энтропии, как и понятие о температуре, приложимо лишь к системам хаотического характера, которые, подобно, например, газу, состоят из громадного числа независимых между собой элементов (молекулы, атомы), между которыми распределяется так или иначе данный запас энергии Е, и распределяется по законам случайных событий. При данном  количестве газа (N молекул) с объёмом V и энергией Е то или иное распределение молекул в пространстве, то или иное распределение энергии но отдельным молекулам даёт разные состояния газа, в разной мере устойчивые и в разной мере вероятные. Энтропия S есть мера этой вероятности w и, вообще говоря, её функция:

Вероятность двух независимых между собой событий равна произведению вероятностей этих событий (см. ХLI, 7, 329):

а энтропия двух независимых между собою физических систем равна сумме их энтропий:

Таким образом имеем:

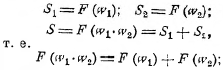
дифференцируя это уравнение по w₁, считая w₂ постоянным, имеем

а дифференцируя обе части этого равенства по w₂ (при постоянном w₁), получаем:

где для краткости положено у = w₁w₂. Отсюда, интегрируя это уравнение, получаем:

где л — универсальная постоянная, lg — натуральный логарифм, а С — неопределённая постоянная. Как определить теперь w? Для примера рассмотрим опять идеальный газ из N одинаковых молекул. Если x, y, z — координаты одной молекулы:  ξ, η, ζ — слагающие скорости её поступательного движения, то число молекул, лежащих в объёме dx·dy·dz и имеющих скорости между

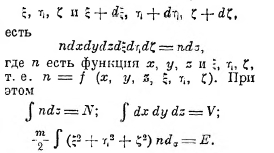
Разобьём весь газ на одинаковые области dσ; перенумеруем их цифрами 1, 2 ... , и пусть в этих областях находятся n₁, n₂. . . молекул. Таких распределений, вполне тождественных между собою, будет очень много, ибо n₁, n₂. . . можно составить из разных молекул. Так, например, если у нас 5 молекул и три области, то распределение: 2, 2, 1 может быть выполнено тридцатью способами; так, беря молекулы № 1 и № 2, имеем комбинации:

3; 1, 2; 4, 5; 4; 1, 2; 3, 5; 5; 1, 2, 3, 4, т. е. три комбинации; таким же манером, исходя из пар

1, 3; 1, 4; 1, 5; 2, 3; 2, 4; 2, 5; 3, 4; 3, 5; 4, 5,

получим всего 30 способов.

Точно так же, если у нас 4 молекулы распределяются на 2 области по две, то число комбинаций будет 6. Это ведёт к формуле числа распределений

N1

где N = 1, 2, 3 ... w, n! = 1, 2, 3 ... n₁ и т. д. Если это число распределений разделить на общее число всех возможных распределений, мы получим вероятность состояния w; но благодаря тому, что в выражение S входит Const, мы можем lg этого общего числа, умноженный на k, включить в смысл Const и тогда будет просто

Но по теореме Стирлинга при большом N будет N! = (N/e)^N, где е есть основание неперовых логарифмов, т.е. мы имеем lg N! = N (lg N — 1), поэтому получается:

или, заменяя сумму S интегралом, имеем просто

где все постоянные включены в Const. Это выражение годно для всякого состояния газа. В устойчивом равновесии это S должно быть наибольшим при данных v, N, Е. Но при бесконечно-малом изменении f на  δf вблизи максимума S будет δS = 0 при условии, что и δN = 0 и δE = 0,так как N и E не изменяются. Это даёт

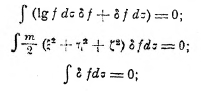
отсюда следует

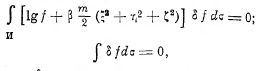
где β — постоянная; и это условие удовлетворяется только, если будет

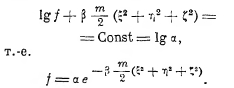
Таким образом, оказывается, что при условии стационарного состояния (устойчивого равновесия) идеального газа f не зависит от х, у, z, т. е. молекулы распределены в объёме равномерно, а зависимость f от  ξ, η, ζ даётся так называемым законом Максвелла. Постоянные α и β найдутся из условий, что:

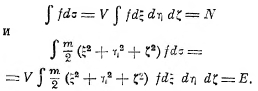
Таким образом, мы получаем энтропию идеального газа

Здесь k дано в механической мере; поэтому мы имеем

т. е. при постоянном V и при постоянной Е мы имеем

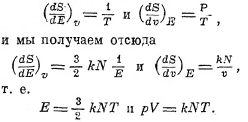
Для граммолекулы одноатомного газа (см. XLI, ч. 7, 494) мы имеем

N есть универсальная постоянная; отсюда получаем

Мы определили таким образом k и пришли к основным свойствам идеального газа.

Энтропия  присуща всякой хаотической системе, у которой энергия может быть распределена по элементам (в пространстве или по времени) по законам случая. Беспорядочность здесь — необходимое условие; чисто периодическая плоская волна не имеет ни энтропии, ни температуры, так как в ней нет характера беспорядочности, хаоса, как этого нет при движении одной молекулы. Но беспорядочное взаимодействие очень многих колебаний разных периодов, распространяющихся в пространстве по разным направлениям, или группа очень многих молекул, беспорядочно движущихся, удовлетворяют условию хаотичности, и тогда можно говорить об энтропии и температуре и в пространстве, где другой энергии, кроме энергии волн, нет. Такова энтропия и температура т. н. чёрного тела, чёрного излучения (см. излучение). И здесь, с одной стороны,

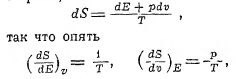
где S и Е относятся к объёму V, наполненному чёрным излучением, с другой стороны,

где W — число распределений энергии по отдельным колебаниям, соответствующее случаю устойчивого равновесия системы, т. е. максимальной энтропии:

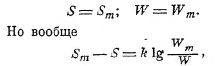
и при k = 1,34·10^-16 даже в том случае, когда S_m—S = 1,34·10^-6, будет W = W_mе^10-10, т. е. оказывается W колоссально мало сравнительно с W_m. Если различие S от S_m будет больше, W будет ещё меньше. Таким образом, оказывается, что все W, отличные от W_m, так малы сравнительно с последней, что без ошибки в выражении для S_m можно брать вместо W_m просто сумму W_m + W + ... всех возможных распределений энергии на отдельные колебания, а это число легко определить. Так, если Е есть вся энергия полости чёрного тела, а N —всё число всех возможных колебаний, то, беря достаточно маленькое количество энергии ε,  мы разделим весь запас энергии на Р = Е/ε частей. Тогда эти Р частей между двумя колебаниями можно распределить следующими способами:

т. е. этих распределений получается Р + 1, и мы можем написать:

Если N = 3, то, оставляя одно колебание без энергии, мы получим Р+1 распределений; давая же этому колебанию энергию ε, получим ещё Р распределений; давая энергию 2ε, получим ещё Р—1 распределений и т. д. Всё число распределений энергии Р_ε на 3 колебания будет поэтому

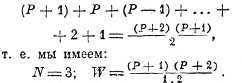
Закон составления W ясен: и при N колебаниях будет

Это можно написать, введя в числитель и знаменатель произведение Р·(Р—1) ... 3.2.1 = Р!

Если Р и N очень велики, как это обычно имеет место, то, пользуясь теоремой Стирлинга, как это мы делали выше, получаем:

после простых преобразований это даёт:

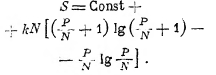
Вводя сюда вместо Р энергию Е, имеем:

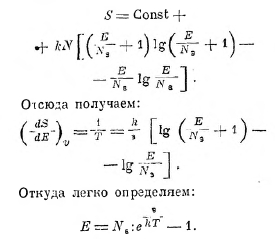
Это — энергия всех колебаний с частотой  v, можно показать легко, что

где С есть скорость света в пустоте. Поэтому энергия udv единица объёма соответствующего колебаниям с частотой между v и v + dv будет

Так как для волн всех частот  должно не зависеть от v, то это возможно лишь, если  ε будет пропорционально v, т. е. если ε = hv, где h — универсальная постоянная; тогда получается т.н. закон Стефана (см. XXI, 48):

Казалось бы, что, разделив энергию Е на Р очень мелких частей ε для того, чтобы иметь возможность вычислить вероятность состояния и энтропии, мы должны в конце концов были бы перейти к пределу, беря ε равное нулю; однако, в этом случае, как легко видеть, получится

и эта формула не дает согласного с опытом выражения для udv. Таким образом, оказывается, что нельзя брать ε= 0: и энергия чёрного излучения оказывается сложенной из величин ε, т.н. квантов энергии (см. об этом излучение), а также энергия, стб. 195 (96 сл.).

Литература: см. в статьях: теплота, излучение; сверх того: Гольдгаммер Д. А., «Теория квант и лучистая энергия», Физическое обозрение, Киев, 1914, т. XV, № 4-5.

Д. Гольдгаммер.

Статистическое истолкование второго начала термодинамики имеет огромное философское значение.

1. Когда Клаузиусом было установлено второе начало термодинамики, то из него сделали вывод, что энтропия мира, непрерывно возрастая, стремится к своему максимуму, и что вселенная благодаря этому приближается к своему «конечному» состоянию, к состоянию т. н. «тепловой смерти». Действительно, на первый взгляд второе начало термодинамики приводит как будто к тому, что все различия в температуре должны выравниваться, а тогда количество механической энергии, которая может возникать за счёт тепловой, будет становиться всё меньше и меньше, так как отношение полученной механической энергии А к затраченной тепловой Q (см. выше), равное (T₁-T₂)/T по мере приближения T₁ к T₂, т. е. по мере выравнивания температуры, приближается к нулю. Таким образом, в мире как будто наблюдается односторонний процесс, при котором количество энергии в форме тепла всё более и более увеличивается за счёт других форм, а тепловая энергия при процессе выравнивания температуры всё меньше и меньше оказывается способной к превращению в другие формы энергии. Короче: мир движется к своему неизбежному концу, именуемому «тепловой смертью». Статистический взгляд на второе начало в корне подрывает эту «теорию» тепловой смерти и связанные с нею религиозные предрассудки.

2. Со статистической точки зрения подробно развитой Больцманом, такие процессы, при которых энтропия убывает, хотя и очень маловероятны, но не являются по существу невозможными. Эта мысль была выражена Риллардом Гиббсом, основателем современной статистической механики, в следующих словах: «Невозможность некомпенсированной убыли энтропии, по-видимому, сведена к невероятности» (Gibbs, «Transactions of the Connecticut Academy», том III, 1875, стр. 229). В работах Смолуховского, последователя Больцмана, эта статистическая точка зрения получила дальнейшую блестящую разработку. Смолуховскому удалось для случая видимых под микроскопом мельчайших взвешенных в воде частиц — т.н. броуновских частиц — вычислить вероятность повторения т. н. маловероятных событий, которая и была потом проверена на опыте.

Опыт производится следующим образом. Под микроскопом помещается препарат, состоящий из капли воды, в которой взвешены какие-либо маленькие частицы (например, частички гумми-гутта). Эти частицы под влиянием ударов окружающих молекул находятся в непрерывном движении. При помощи надлежащим образом выбранных диафрагм можно в поле зрения выделить небольшую часть препарата так, чтобы в ней было видно небольшое число частиц, которые можно было бы легко подсчитать. Так, в одной серии наблюдений, выполненных Сведбергом, выделенная часть поля зрения была такова, что в ней в среднем было видно n = 1,53 частицы. В отдельные  моменты число видимых частиц n было равно 0; 1; 2; 3; 4; 5; 6, причём числа 4, 5, 6 наблюдались редко.

Смолуховскому, путём крайне остроумных расчётов, удалось подсчитав средние промежутки времени Θ_n, отделяющие последовательные появления n частиц. Эти величины Θ_n были вычислены для различных чисел частиц n (при среднем n=1,53 для упомянутой выше серии наблюдений Сведберга). Эти вычисленные величины «среднего времени возврата Θ_n» были проверены путём сравнения с наблюдёнными Сведбергом величинами. Измерения производились следующим способом: поле зрения при помощи моментального затвора освещалось через определённое число секунд на некоторую долю секунды, в течение которой отмечалось число видимых частиц. Результаты сравнения теории с опытом приведены в следующей таблице:

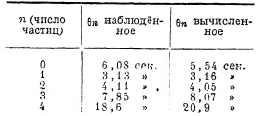
Совпадение теории с опытом надо считать вполне удовлетворительным, принимая во внимание, что число 18,6 сек. взято как среднее из очень небольшого числа измерений.

3. Какой смысл имеет, скажем, повторное наблюдение четырёх частиц через каждые 18,6 сек.? Так как среднее число частиц, наблюдаемое в данном участке поля зрения, n =1,53, то число частиц = 4 означает, что в данный момент концентрация частиц значительно больше средней, а потому в силу законов диффузии число частиц должно уменьшиться. По законам классической термодинамики процесс диффузии — процесс необратимый, и действительно, если два газа смешаются в процессе диффузии, то они ведь сами собой вновь уже не разделяются! Из таблицы же видно, что процесс диффузии для 4 частиц через каждые 18,6 сек. идёт в противоположном направлении, так что рассмотренный нами процесс диффузии для четырёх частиц (при среднем n = 1,53), по выражению Смолуховского, является процессом «обращающимся». Смолуховский подсчитал, что если бы в данном участке поля зрения было не 4, а 8 частиц, то повторное наблюдение 8 частиц происходило бы в среднем уже не через каждые 186 сек., а через каждые 2 часа. Для этого случая мы имеем только вычисленную величину, так как для получения опытных данных надо было бы опыты вести непрерывно в течение нескольких десятков часов, чего не было сделано, но что принципиально возможно. Для числа частиц n=10 время возврата достигает 2 ½  суток, для n=14 оно равняется уже 30 годам, а для n = 17 время возврата равно огромной величине в 34 000 лет!

Таким образом, время возврата растёт с числом частиц изумительно быстрыми темпами, а кроме того время, требуемое для проверки этого результата теории, вступает в тяжёлый конфликт со средней продолжительностью человеческой жизни. Вот почему случай диффузии 17 частиц является для нас процессом необратимым, тогда как обращение процесса диффузии 4 частиц (и то и другое при среднем n=1,53) происходит на наших глазах каждые 18,6 сек. Отсюда ясна вся относительность того, что мы называем необратимым процессом.

4. Больцман и Смолуховский считают, что возникновение мира порядка нашей системы Млечного пути надо рассматривать как очень маловероятное событие, которое, однако, на протяжении несметных промежутков времени должно произойти с такой же закономерностью, с какой в рассмотренном нами выше примере через каждые 18,6 сек. под микроскопом появляются по 4 частицы, тогда как в среднем их там будет только n = 1,53. Эта точка зрения подтверждается данными астрофизики. Уже давно было установлено, что среди видимых звёзд мы имеем сравнительно большое число т. н. красных звёзд, т. е. звёзд потухающих. Это как будто подтверждало т. н. «тепловую смерть». Однако на рубеже XIX и XX столетий Рёссель и Герцшпрунг показали, что в число красных звёзд попали две группы звезд, именно: действительно потухающие, т. е. остывающие звёзды, и разгорающиеся, т. е. те, которые только что образовались из туманности и которые находятся на «восходящей линии» своего развития (ср. эволюция небесных тел, LI, 4/8). Статистика показывает, что число разгорающихся звёзд — того же порядка, как и число потухающих, и, таким образом, мир вовсе не стремится к своему концу, а являет собой диалектический процесс возникновения, развития и гибели отдельных миров, их нового возникновения и т. д.

Больцман и Смолуховский своими физическими исследованиями, оснащёнными блестящими математическими построениями, положили начало детальному изучению этого величественного процесса, подтверждая тем самым пророческие предсказания Энгельса: «Но здесь мы вынуждены . . . либо обратиться к помощи творца, либо сделать тот вывод. . что раскалённый сырой материал для солнечной системы нашего мирового острова возник естественным путём, путём превращений движения, которые присущи от природы движущейся материи и условия которых должны, следовательно, быть снова произведены материей (ср. выше «обращающиеся» процессы Смолуховского — А .Т.), хотя бы после миллиардов лет, более или менее случайным образом, но с необходимостью, присущей и случаю» (Маркс и Энгельс, Соч., т/ХІV, стр. 490).

Необходимо, однако, сказать, что Больцманом и Смолуховским сделаны только первые шаги. В настоящее время очень важной для данного вопроса является задача выяснения природы космического излучения и связанного с его возникновением и поглощением преобразования энергии.

Л. Тимирязев.