Эпициклоида

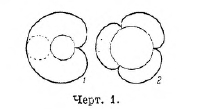
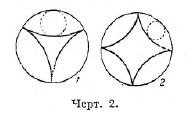
Эпициклоида и гипоциклоида, кривые, принадлежащие к числу рулет (см. XIII, 319/20, приложение, 47/48), описываемые точкой окружности круга, катящегося (без скольжения) по другому – неподвижному кругу. Когда катящийся круг касается неподвижного извне, точка описывает эпициклоиду (черт. 1), когда касание внутреннее – гипоциклоиду (черт. 2).

Если через а обозначить радиус неподвижного, через b — радиус катящегося круга, а за параметр t принять угол поворота катящегося круга, то уравнения эпициклоиды в параметрической форме напишутся в следующем виде:

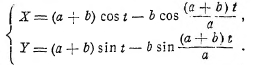
(Уравнения гипоциклоиды можно получить из уравнений эпициклоиды заменой b на —b).

Вид кривой зависит от отношения радиусов подвижного и неподвижного кругов. Если отношение a/b число рациональное, то кривая замкнута;

При б = а эпициклоида принимает вид сердцевидной кривой, носящей название кардиоиды (черт. 1, 1). При внутреннем касании, когда радиус подвижного круга в 4 раза меньше радиуса неподвижного, получается гипоциклоида с 4-мя заострениями, звездчатая кривая — астроида (черт. 2, 2); когда радиус подвижного в 2 раза меньше радиуса неподвижного круга, то траекторией точки оказывается диаметр неподвижного круга (гипоциклоида вырождается в отрезок прямой), вдоль которого точка колеблется взад и вперёд; на этом, между прочим, основано преобразование вращательного движения в колебательное прямолинейное в некоторых механизмах (иногда применяется в типографских скоропечатных машинах).

Длина одной арки эпициклоиды (при изменении t от 0 до 2π) может быть найдена по формуле:

для гипоциклоиды — по формуле:

Если точка, описывающая кривую, берётся не на окружности катящегося круга, а внутри или вне его, то получаются укороченная или удлиненная эпициклоида и гипоциклоида, называемые эпитрохоидой и гипотрохоидой (см. XIII, 319/20, прил., 48).

А. Дюрер первый, по-видимому, рассматривал (1525) свойства эпициклоиды. В XVII в. этими кривыми занимались Де-ла-Гир, Дезарг, Ньютон и др.

А. Ш.