Функции гармонические

Функции гармонические. Функции гармонические двух независимых переменных х, у называют функцию V(х, у), которая в данной области (см. функция) непрерывна, однозначна с таковыми же производными 1-го порядка, допускает производные 2-го порядка и удовлетворяет уравнению Лапласа:

Из определения функции гармонической выводится, что она допускает непрерывные производные любого порядка и что она аналитическая функция двух переменных х, у, т. е. в окрестности любой точки (х₀,у₀) области разлагается по степеням разностей (х — х₀), (у — х₀) в ряд Тэйлора;

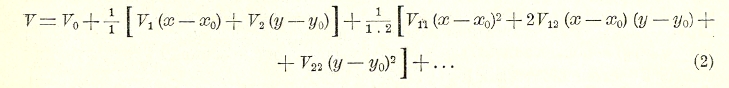
где V₀, V₁, V₂, V₁₁, V₁₂, V₂₂,... значения V и ее производных 1-го, 2-го,... порядков в точке (х₀,у₀). Все частные производные функции гармонической — тоже функция гармоническая, как легко убедиться, дифференцируя уравнение (1). Функция  гармоническая двух действительных переменных х, у находится в тесной связи с аналитической функцией комплексного переменного х+iy (см. функция).

Если имеем две функции U, V гармонические в области, ограниченной контуром С, то, на основании так называемой теоремы Грина, для них имеет место соотношение

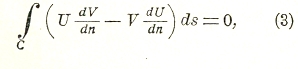
где интеграл берется по контуру С, ds — дифференциал дуги контура, dV/dn и dU/dn —  производные по нормали. Полагая U=1, получаем соотношение

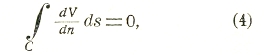
имеющее место для всякой гармонической в данной области функции (в предположении, что на контуре С существуют частные производные  ∂V/∂x, ∂V/∂y, линейной комбинацией которых является dV/dn).

Непосредственным вычислением можно убедиться, что функция log 1/r, где

т. е. r есть расстояние точки (х, у) от точки (а,b), удовлетворяет уравнению Лапласа (I). Таким образом функция log 1/r есть функция гармоническая везде, за исключением точки (а,b), где она обращается в бесконечность. Пусть мы имеем функцию U гармоническую в области, ограниченной контуром С. Возьмем точку (а,b) внутри этой области и опишем около нее окружность малым радиусом р. Контур С и окружность радиуса р ограничивают двусвязную область (см. функции), к которой применим формулу (3), полагая V=log 1/r. При этом интеграцию придется производить в положительном направлении по контуру С и в отрицательном по окружности (см. черт.). Меняя направление последней интеграции, разбивая интеграл на два и перенося второй во вторую часть равенства, получаем:

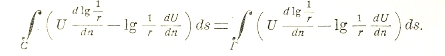
Замечая, что на окружности Г, r=ρ, ds = ρdΘ, где Θ — полярный угол, преобразуя второй интеграл и переходя к пределу для ρ = 0, получаем

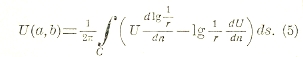
Введем теперь в рассмотрение так называемую функцию Грина данной области. Это есть функция, которая на контуре С равна нулю, везде внутри гармонична, за исключением одной точки (а, b) — полюса, где она обращается в бесконечность, как log 1/r. Обозначая эту функцию через g (x, у, а, b), имеем

где ω (x, у) есть функция уже везде гармоническая в данной области. Применяя формулу (3) к функциям U и ω = g — lg 1/r и пользуясь формулой (5), получаем:

так как на контуре g = 0. Формула (6) позволяет находить значения функции гармонической U в любой точке области по ее значениям на контуре. При этом предполагается, что известна функция Грина для области и что на контуре существуют (непрерывные) производные функции Грина. Доказательство существования функции Грина для любой области было дано Осгудом (Osgood). Задача определения функции гармонической по ее значениям на границе области есть знаменитая задача Дирихле. Формула (6) дает ее решение при сделанных предположениях, но возможность решения этой задачи доказана при самых общих предположениях относительно области и независимо от функции Грина.

Если, в частности, контур С есть окружность, то функция Грина легко строится, и из формулы (6) получаем известную формулу Пуассона

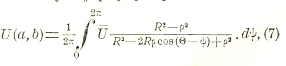
дающую решение задачи Дирихле для круга. В этой формуле R — радиус круга, ρ, Θ — полярные координаты точки (а, b), в которой вычисляется значение функции U; через Ü обозначено значение U на окружности.

Предполагая, в частности, что точка (а,b) совпадает с центром круга, получаем формулу

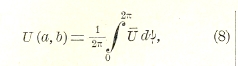
которая может быть легко получена непосредственно и дает значение функции гармонической в центре круга по значениям на окружности; ψ есть полярный угол полярной системы, имеющей полюс в центре (а, b) круга. Из этой формулы явствует, что значение функции гармонической в центре круга есть среднее из значений на окружности (теорема Гаусса), а отсюда следует, что функция гармоническая в области не может достигать ни наибольшего, ни наименьшего значения ни в одной точке внутри области.

Для доказательства, которое ведется от противного, достаточно около точки, в которой, согласно допущению, функция достигает наибольшего или наименьшего своего значения, описать круг достаточно малого радиуса, чтобы он целиком находился внутри области, и применить формулу (8).

Из теоремы о наибольшем и наименьшем значении легко выводится, что задача Дирихле для области, ограниченной любым контуром, может иметь только единственное решение.

В самом деле, пусть U₁ и U₂ две функции гармонической, совпадающие на границе области. Их разность U = U₁ – U₂, очевидно, тоже функция гармоническая, исчезающая на контуре области, а такая функция необходимо равна нулю везде внутри области, так как в противном случае она достигала бы своего максимума или минимума  (положительного или отрицательного) внутри области.

Из классических методов решения задачи Дирихле можно упомянуть о методах Neumann’а, Schwarz’а, Poincaré. Новейшие изыскания по задаче Дирихле принадлежат, между прочим, Hilbert’у, Lebesgue’у, Perron’у, Riesz’у, Люстернику.

Функция V трех независимых переменных х, у, z называется функция гармоническая в области пространства трех измерений, если она допускает непрерывные производные и удовлетворяет уравнению Лапласа в трех переменных

Интегральные соотношения, приведенные выше, сохраняют силу для функций гармонических трех переменных при замене интегралов по контуру интегралами по поверхности, ограничивающей область.

Таким образом имеем

где dσ — элемент поверхности, и интеграция распространена на границу области.

Из этой формулы сходными рассуждениями выводятся заключения, аналогичные тем, которые приведены выше. При этом лишь следует заменить функцию log1/r функцией 1/r , где

которая, как легко видеть, удовлетворяет уравнению Лапласа (9).

В результате имеем, между прочим

где двойной интеграл справа распространен на поверхность сферы радиуса R, имеющей центр в точке (а,b,с) и. dω — элемент поверхности этой сферы. Формула (11) дает теорему Гаусса и теорему о наибольшем и наименьшем значении функция гармоническая, как и в случае двух переменных.

Отсюда следует, что задача Дирихле, которая в случае трех переменных ставится так же, как и в случае двух, может иметь лишь единственное решение.

Решение этой задачи для сферы дается интегралом Пуассона:

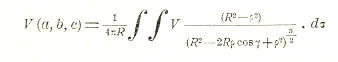
Здесь R — радиус сферы, dσ — элемент ее поверхности, ρ — расстояние точки (а,b,с) от центра сферы, γ — угол между радиусами векторами, проведенными из центра к точке (a, b, с) и к переменной точке поверхности сферы.

Методы Неймана и Пуанкаре применяются к решению задачи Дирихле в пространстве (для трех переменных).

Уравнение Лапласа для трех переменных встречается в целом ряде вопросов механики и физики. Потенциал притяжения в тех точках, где нет притягивающих масс, электростатический потенциал внутри проводника, температура при установившемся тепловом течении — все это функции гармонические.

Д. Егоров.