Функции симметрические

Функции симметрические. Функция f(x₁, х₂,... х_n) нескольких аргументов называется функцией симметрической, если она не изменяется при всевозможных перестановках этих аргументов. Так, например, функция трех переменных x₁, х₂, х₃ есть функция симметрическая, если имеем: f (x₁, х₂, х₃) = f (x₁, х₃, х₂) = f(x₂, х₃, х₁) = f (x₂, х₁, х₃)  = f(x₃, х₁, х₂) = f(x₃, х₂, х₁). Так как всякая перестановка может быть сведена к последовательному взаимному перемещению двух элементов, то функцию симметрическую можно определить иначе, как функцию, не изменяющуюся при перемещении (транспозиции) любых двух аргументов.

Простейшие («элементарные») функции симметрические и аргументов суть:

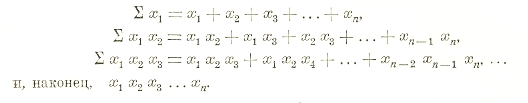
Знак суммования ∑ в теории функции симметрической имеет тот смысл, что берется сумма всех тех выражений, которые получаются из выражения, стоящего  под знаком ∑, всевозможными перестановками букв x₁, х₂,… х_n и которые различны между собою.

Если имеем уравнение n-ой степени

с корнями x₁, х₂,… х_n то непосредственно очевидно, что элементарные функции симметрические его корней равны, со знаком + или —, коэффициентам уравнения:

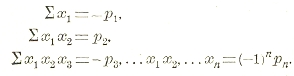
Основное положение всей теории функции симметрической состоит в том, что всякая рациональная функция симметрическая рационально выражается через элементарные функции симметрические.

Рассматривая, как выше, уравнение (1) n-ой степени с корнями x₁, х₂,… х_n, мы это же положение можем высказать в такой форме: всякая рациональная функция симметрическая корней уравнения рационально выражается через коэффициенты уравнения.

Положение это доказывается постепенным сведением функции симметрической к более и более простым. Всякая рациональная функция симметрическая есть частное от деления двух целых функций симметрических, и, таким образом, положение наше приводится к положению: всякая целая функция симметрическая есть целая функция элементарных функций симметрических. Целая функция симметрическая распадается на совокупность «типов», т. е. таких функций, которые получаются из одного члена

суммированием всех различных членов, получающихся из данного всевозможными перестановками. Для такого «типа»

иногда употребляют сокращенное обозначение (i₁, i₂…i_n). Простейшие из типов получим, взяв число показателей i₁, i₂ равное одному. Такая функция симметрическая

есть не что иное как сумма і-ых степеней всех аргументов и обозначается обыкновенно через s_i.

Для функций s_i легко выводятся формулы Ньютона:

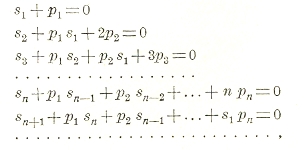
из которых s_i легко вычисляется через коэффициенты р₁, р₂,...р_n уравнения (1) или, что то же, через элементарные функции симметрические.

Типы с двумя и более показателями (i₁ i₂), (i₁ i₂ i₃),... при помощи формул Варинга приводятся к суммам s_i. Для примера выполним приведение для функции

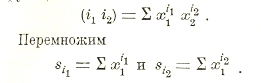
При умножении правых частей, очевидно, получим всевозможные члены вида x₁ⁱ¹ x₂ⁱ², а также члены вида x₁ⁱ¹⁺ⁱ², и, таким образом, имеем

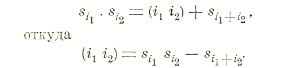
Для приведения любой целой функции симметрической к элементарным симметрическим существуют методы Баринга и Гаусса, Коши, Кронекера.

Таблицы, дающие выражения функции симметрической через элементарные функции, составлялись Вандермондом, Кэли, Мак-Магоном и другими.

Д. Егоров.