Функции

Функции. Понятие о функциях появляется в математике в конце XVII и начале XVIII столетия. Самый термин «функция» в том смысле, в котором мы его употребляем, по-видимому впервые встречается у Ивана Бернулли (1698). Эйлер дает уже элементарную классификацию функций на алгебраические и трансцендентные, явные и неявные, однозначные и многозначные и дальнейшую классификацию алгебраических функций на иррациональные и рациональные и этих последних на целые и дробные (см. высшая математика). Ближайшим поводом для обобщения и уточнения понятия о функциях послужила знаменитая «задача о колеблющейся струне», вызвавшая целый ряд работ всех выдающихся математиков ХVІII и начала XIX столетия.

Определение функций, которое можно считать современным, впервые точно формулировано было Лежен-Дирихле (1837). Согласно этому определению количество у есть функция количества х в данном промежутке а≤х≤b, если каждому значению х в этом промежутке соответствует определенное значение у.  Можно сказать иначе, что функциональная зависимость имеется в том случае, когда установлено соответствие: между двумя множествами (совокупностями чисел). Одно из них объединяется символом х (числовые значения х), другое символом у (числовые значения у), и мы говорим, что у есть функция х, если каждому элементу первого множества соответствует определенный элемент второго.

Определение Дирихле собственно относится только к однозначным функциям и притом от одного переменного, но непосредственно распространяется на многозначные функции и на случай многих  переменных: u есть функция переменных х₁, х₂,…х_n, если каждой системе значений х₁, х₂,…х_n соответствует одно или несколько (может быть даже бесчисленное множество) значений u. В общей теории функций обычно рассматривают почти исключительно однозначные функции; это тем более естественно, что многозначные функции, поскольку они появляются в анализе, допускают обычно разбиение на несколько однозначных функций; например, двузначную функцию √х для действительных значений х можно рассматривать как совокупность двух однозначных функций +√х и —√х. В определении Дирихле не налагается никаких ограничений на соответствие, которое предполагается между значениями  х и у. В последнее время со стороны многих математиков выставляется требование, чтобы это соответствие действительно фактически могло быть установлено, чтобы, иначе говоря, был дан какой либо закон, устанавливающий это соответствие.

Исследования по теории функций объединяются в настоящее время в два различных отдела: исследования, исходящие из общего определения функций, ведутся в предположении исключительно действительных значений переменных и потому относятся к так называемой теории функций действительного переменного; наряду с этим рассматривается  важный частный класс функций, так называемых аналитических функций, и эти функции изучаются в области всевозможных комплексных значений аргумента; теория их поэтому называется теорией функций комплексного переменного.

Теория функций действительного переменного самым тесным образом связана с одним из новейших отделов математики — теорией множеств (совокупностей элементов). Упомянем лишь самое необходимое для дальнейшего из области этой теории. Простейшие бесконечные множества — это те, элементы которых можно привести во взаимно-однозначное соответствие с рядом целых чисел 1,2,3,4,..., n,... или иначе — можно перенумеровать, расположив в последовательность u₁, u₂, u₃, u₄,… u_n,... Такие множества называются счетными. Рассмотрение класса так называемых вполне упорядоченных бесконечных множеств и введение для них понятия, аналогичного понятию числа элементов конечного множества, приводит к продолжению ряда натуральных чисел 1, 2, 3, 4, ... «за бесконечность», к созданию так называемых трансфинитных чисел, или трансфинитов. Если ограничиться рассмотрением множеств, элементы которых суть действительные числа (или группы чисел), то, прибегая к обычному геометрическому истолкованию, можно говорить о множествах точек, и, таким образом, выделяется важный отдел теории множеств — теория точечных множеств, имеющая особенное значение для теории функций действительного переменного, в которой и значения переменных независимых и значения функций суть действительные числа.

Верхней гранью множества чисел Е называют такое число А, которого не превосходит ни одно число множества Е, но вместе с тем обладающее тем свойством, что в множестве Е всегда найдутся числа, превосходящие любое число А — ε, меньшее А. Если число А есть само одно из чисел множества Е, то оно называется максимумом множества Е. Аналогично определяются нижняя грань и минимум.

 Предельной точкой точечного множества, лежащего на прямой, или в плоскости или в пространстве, называется такая точка, в любой близости которой имеются точки множества. Множество, содержащее свои предельные точки, называется замкнутым. Замкнутое множество, все точки которого суть предельные точки множества, называется совершенным.

Рассмотрим линейное множество, т. е. множество точек Е на прямой. Для простоты предположим, что оно помещается на отрезке от нуля до единицы. Покроем точки множества Е счетным множеством отрезков и вычислим сумму L длин этих отрезков. Множество чисел L, для всевозможных выборов системы отрезков, имеет нижнюю грань, которая называется внешней мерой множества Е. Множество Е точек отрезка [0, 1], не принадлежащих к Е, называется дополнительным к Е. Разность длины отрезка [0, 1] и внешней меры множества дополнительного к Е называется внутренней мерой множества Е. Множества, для которых внешняя и внутренняя мера совпадают, называются измеримыми (по Лебегу), и общая величина внешней и внутренней мер называется их мерой (по Лебегу).

Аналогично определяется мера плоскостных и пространственных множеств.

Частным случаем измеримых множеств являются множества измеримые по Борелю, или так называемые В-множества. Борель определяет меру линейного множества при помощи следующих принципов: 1° мера отрезка равна его длине (для плоскостного множества — мера квадрата равна его площади и т. д.); 2° мера суммы конечного или счетного множества множеств, не имеющих попарно общих точек, равна сумме их мер; 3° если множество Е меры S содержит все точки множества Е' меры S', то мера разности этих множеств, т. е. множества, состоящего из всех точек Е, не принадлежащих к Е', равна разности S — S' мер этих множеств. Множества, меру которых можно определить, исходя из этих принципов, и суть В-множества. Мера такого множества по Борелю совпадает с его мерой по Лебегу.

После этого отступления возвращаемая к теории функций действительного переменного, причем для простоты будем ограничиваться случаем одного независимого переменного.

Рассмотрим промежуток изменения переменного а ≤ x ≤ b. Множество значений, принимаемых функций f(x) в этом промежутке, имеет верхнюю и нижнюю грани¹⁾, которые называются верхней и нижней гранью функций в промежутке [a,b].

¹⁾ Грани эти могут быть и бесконечно велики. Если обе они конечны, то функция называется ограниченной в промежутке.

Рассмотрим далее какое-нибудь значение переменного х₀ и соответствующую ему на оси x точку А. Для любого промежутка, содержащего точку А, функция f(x) имеет верхнюю грань М. Эти числа М для всевозможных промежутков, содержащих А, образуют множество чисел, имеющее нижнюю грань М (f, А), которая называется верхней гранью функций f(x) в точке А. Аналогично определяется нижняя грань m (f, А), функции в точке А. Разность М (f, А), — m (f, А) называется колебанием функций в точке А. Если колебание функций в точке равно нулю, то функций в этой точке, или, что то же, для этого значения переменного, непрерывна. Так как вообще имеем, очевидно, m (f, А) ≤ f  (A) ≤ M (f, А), то в точке непрерывности М (f, А) = m (f, А) = f (А), где через f (А)  обозначено значение функций в точке А. Если имеет место только равенство f (А) = M (f, А), то функция называется полунепрерывной сверху в точке А; аналогично, если f (А) = m (f, А), то функция полунепрерывна снизу в точке А. Легко убедиться, что если функция f (х) непрерывна для значения переменного х₀ и если переменное х стремится к значению х₀ (принимая, например, последовательность значений х₁, х₂, .. . имеющих пределом х₀), то значения функции стремятся к значению ее для х = х₀, так что

Если функция непрерывна для всех значений х в некотором промежутке, то функция называется непрерывной в этом промежутке; если функция непрерывна вообще для всех рассматриваемых значений х, то она называется непрерывной. В силу теоремы, доказанной Вейерштрассом, функцая, непрерывная в каком-либо промежутке, может быть с любой точностью в этом промежутке представлена многочленом, а следовательно всякая непрерывная в каком-либо промежутке функция может быть представлена в этом промежутке равномерно   сходящимся рядом многочленов:

где Pk (х) — многочлен.

Точки, в которых функция не непрерывна, называются точками разрыва. Пусть А есть такая точка для функции f(x), соответствующая значению х = х₀. Рассмотрим всевозможные отрезки оси х, имеющие правым концом точку  А. В каждом из таких отрезков, с выключением его конца А, можно рассматривать верхнюю и нижнюю грани f (x). Множество чисел — верхних граней f (х) в упомянутых отрезках — имеет нижнюю грань, которая называется верхней гранью f(x) слева от А; точно так же верхняя грань множества чисел — нижних граней f(x) в упомянутых отрезках — есть нижняя грань f (х) слева от А.

Аналогично определяются верхняя и нижняя грани f(х) справа от А.

Если верхняя и нижняя грани слева от А совпадают, то значения функций при приближении точки к точке А слева стремятся к некоторому пределу, который обозначают f (х₀—0). Равным образом, если совпадают верхняя и нижняя грани справа от А, то значения функций справа от А стремятся к пределу f(x₀ + 0). Если при этом f (х₀—0) = f(х₀), то функция в точке А непрерывна слева; если же f(x₀+0) = f(x₀), то она непрерывна справа.

Если совпадают верхние и нижние грани одновременно справа и слева, так что существуют пределы, обозначаемые f(х₀ — 0) и f(х₀ + 0), то точка А называется точкой разрыва 1-го рода, или точкой конечного скачка; величина скачка измеряется абсолютной величиной разности f (х0+0) — f (х₀ — 0).

Если хотя бы с одной стороны точки А верхняя и нижняя грани функций не совпадают, то точка А называется точкой разрыва 2-го рода, или точкой разрыва с колебаниями.

К точкам разрыва обычно относят и те точки, в которых функция получает бесконечные значения. В такой точке верхняя или нижняя грань функций необходимо равна бесконечности. Однако, обратное заключение несправедливо. Равным образом функция может быть конечна во всех точках некоторого промежутка, а между тем верхняя или нижняя грань ее в этом промежутке может быть бесконечно велика. Так, например, функция, на отрезке [0,1] равная нулю для х = 0 и 1/х для всех прочих значений х, везде конечна; в этом промежутке, но верхняя грань ее равна + ∞. Таким образом, эта функция в промежутке [0,1] везде конечна, но не ограничена. Изложенное замечание находится в связи с выше установленным различием между верхней гранью функций и максимумом, нижней гранью и минимумом. Функция, вообще говоря, может в данном промежутке не достигать своей верхней или нижней грани. Для непрерывных функций имеет место теорема: функция, непрерывная в данном промежутке, включая его концы (на данном отрезке), достигает в нем своей верхней и нижней грани, которые, таким образом, являются ее максимумом и минимумом. Теорема эта имеет силу и в том случае, если вместо отрезка рассматривать какое-либо замкнутое множество значений х.

Функция  называется в данном промежутке монотонной (возрастающей или убывающей), если с возрастанием значений независимого переменного ее значения не убывают или же не возрастают. Разностью двух монотонных функций можно всегда выразить функцию, принадлежащую к важному классу так называемых функций с ограниченным изменением (а variation bornée). Функция  f(х) обладает ограниченным изменением в промежутке [а, b], если при всевозможных разбиениях этого промежутка на частичные промежутки (помощью введения промежуточных точек х₁, х₂, . . . х_n) сумма колебаний f(х) в этих промежутках остается ограниченной, не превосходящей некоторого числа М. Легко усмотреть, что функция с ограниченным изменением в данном промежутке может иметь в нем лишь счетное множество точек разрыва, притом все они необходимо — 1-го рода (это очевидно для монотонных функций, а, следовательно, в силу ранее сделанного замечания, имеет место и для функции с ограниченным изменением).

Выше мы видели (теорема Вейерштрасса), что всякая непрерывная функция может быть представлена равномерно сходящимся рядом многочленов. Так как сумма конечного числа многочленов есть многочлен, то можно также сказать, что непрерывная функция может быть представлена как предел многочлена:

причем стремление к пределу здесь имеет место равномерно, т. е. для любого (сколь угодно малого) числа ε всегда можно выбрать такое целое число N, чтобы для всех n≥N имело место неравенство

для всех рассматриваемых значений х одновременно.

Этот результат дает повод поставить общую задачу об аналитическом представлении  функций. Лебег называет функцию аналитически представимой, если значение ее для каждого значения переменного можно построить, совершая по определенному закону конечное число или счетное множество операций сложения, умножения и перехода к пределу, исходя из значения переменного и постоянных. Может показаться странным, почему в этом определении исключены некоторые операции, как, например, деление, но дело в том, что все они могут быть выражены через вышеупомянутые.

Задача эта разрешена Лебегом, охарактеризовавшим функции, аналитически представимые, и Бэром, давшим их классификацию. Классы Бэра строятся следующим образом. Исходный, нулевой, класс образуют непрерывные функции. Равномерно-сходящийся ряд непрерывных функций есть, как известно, опять-таки непрерывная функция. Но ряд неравномерно сходящийся, члены которого непрерывные функции, может иметь прерывную сумму. Функции  1-го класса определяются, поэтому, как суммы рядов непрерывных функций в том случае, когда сумма ряда не есть непрерывная функция. Иначе (т. к. сумма ряда есть предел суммы конечного числа его членов) можно сказать, что функции 1-го класса определяются как пределы функций непрерывных в том случае, когда этот предел сам не есть непрерывная функция. Так как, по теореме Вейерштрасса, всякая непрерывная функция может быть с любым приближением представлена многочленом, то функция 1-го класса может быть представлена неравномерно сходящимся рядом многочленов

Функции  2-го класса определяются как пределы функций 1-го класса, если только этот предел сам не есть функцией 0-го или 1-го класса. Очевидно, что всякая функция 2-го класса может быть представлена двойным рядом многочленов

Классификация продолжается аналогично дальше: функция n-го класса определяется как предел функций (n — 1)-го класса, если только этот предел не есть функция низшего класса. Функция  n-го класса может быть представлена n-кратным рядом многочленов.

Но этого мало: пусть имеем сходящуюся последовательность f₁(x), f₂(x), f₃(x), . . . функций возрастающих классов (например, пусть класс функции равен ее индексу). Предел

есть, вообще, функция класса, который выше всякого конечного класса. Мы получаем, таким образом, первый трансфинитный класс, класс ω. За ним следуют классы (ω + 1)-й, (ω +2)-й и т. д. Например, функции (ω + 1)-го класса определяются как пределы функций класса ω. Доказано, что существуют функции любого трансфинитного класса, так что классификация Бэра не пустая, а вполне реальная.

Все функции, входящие в классификацию Бэра, очевидно, аналитически представимы, но и обратно, как показал Лебег, аналитически представимая функция входит в классификацию Бэра.

Можно указать общее свойство, характерное для всех функций этой классификации.

Рассмотрим множество тех значений х, для которых

где α, β — два любых числа. Если f(x) функция, входящая в классификацию Бэра, то упомянутое множество есть множество измеримое по Борелю, или В-множество (см. выше), и обратно, если для любых α и β рассматриваемое множество есть В-множество, то f(х) входит в классификацию Бэра и аналитически представима.

Так как В-множества являются лишь частным случаем множеств вообще и в частности измеримых (по Лебегу) множеств, то отсюда можно заключить, что функциями, входящими в классификацию Бэра, не исчерпывается все многообразие функций. Так оно и есть в действительности. Функции, входящие в эту классификацию, являются частным случаем того обширного класса функций, которые называются измеримыми и которые обычно и рассматриваются в современной теории функций действительного переменного. Функция  f(х) называется измеримой, если множество тех точек х, для которых

есть измеримое (по Лебегу) множество для любых α и β. Во всех почти построениях теории функций, функция f(x) предполагается измеримой; если в частности она измерима В (по Борелю), то есть если множество, выше упомянутое, есть В-множество, то f (х) — аналитически представима и входит в классификацию Бэра. Функции  измеримые, но не входящие в классификацию Бэра, реально существуют, и примеры таковых функций построены.

Что касается до вопроса о существовании неизмеримых функций, то дело обстоит следующим образом: хотя, казалось бы, самый факт существования неизмеримых функций не должен бы возбуждать сомнений, но дать какой-либо пример подобной функции не представляется возможным, если не опираться на одно положение теории множеств, так называемую аксиому Цермело (Zermelo), признание которого ведет к заключениям трудно приемлемым и которое поэтому нельзя считать общепризнанным в математике.

Для всех измеримых функций характерным является свойство, называемое С-свойством (по терминологии Н. Н. Лузина). Всегда можно для данной измеримой функций f(х) и данного сколь угодно малого число ε построить непрерывную функцию, совпадающую с f(x) везде, кроме точек множества меры = ε. Можно короче сказать, что всякая измеримая функция «непрерывна до ε». Отсюда можно заключить, что всякую измеримую функцию можно представить рядом непрерывных функций, а значит и рядом «полиномов, сходящимся к ней почти всюду», т. е. везде, за исключением множества меры нуль.

Возвращаясь к классификации Бэра, следует сказать, что хотя она и не охватывает, как мы отметили, всего множества функций, но можно сказать, что все существенно важные типы функций, встречающиеся в анализе, покрываются классами Бэра.

Непрерывные функции, как было указано, образуют нулевой класс. Первый класс содержит разрывные функции, которые могут быть представлены как пределы непрерывных функций Бэр дал общий критерий принадлежности функций к 1-му классу, введя понятие о точечной и о полной разрывности функций. Функция  f(х) называется точечно разрывной на отрезке [а, b], если любая точка этого отрезка или есть сама точка непрерывности, или же в любой близости к ней имеются точки непрерывности. В противном случае функция называется вполне разрывной. Это определение можно распространить, рассматривая вместо отрезка какое-либо совершенное множество точек х, так как совершенное множество имеет то общее с отрезком, что каждая предельная точка его принадлежит к множеству и обратно — каждая точка множества есть предельная точка точек множества. Поэтому, рассматривая значения функций только для точек множества, мы, тем не менее, можем всецело перенести туда обычные определения непрерывности или разрывности функций в данной точке. Критерий, данный Бэром, заключается в следующем: необходимым и достаточным условием принадлежности разрывной функции к 1-му классу является требование, чтобы она была точечно разрывна на любом совершенном множестве в области ее определения.

К функциям, удовлетворяющим этому требованию, очевидно, принадлежат функции, имеющие только конечное число точек разрыва, а также счетно-разрывные функции (точки разрыва которых образуют счетное множество), значит, между прочим, все монотонные функции и все функции с ограниченным изменением. Можно сказать, что все разрывные функции, имеющие практическое значение, исчерпываются 1-м классом Бэра. В качестве примера функции разрывной, но не принадлежащей к 1-му классу, можно привести функцию χ(х), указанную Дирихле, которая равна нулю для всех иррациональных и единице для всех рациональных значений х. На отрезке, где она определена, эта функция, очевидно, разрывна в каждой точке; значит, она вполне разрывна, и легко усмотреть, что она 2-го класса и представляется двойным пределом:

Заметим, наконец, что классификация Бэра распространяется и на функции многих переменных.

Сопоставляя результаты, изложенные выше, с тем, что было сказано в начале о классификации множеств, мы можем заключить, что В-множества образуют класс множеств, допускающих аналитическое определение. В самом деле, множество такого рода всегда может быть определено как множество значений х, удовлетворяющих двойному неравенству

где f(x) функция классификации Бэра и, следовательно, аналитически представимая.

Не следует, однако, думать, что В-множествами исчерпываются аналитически-определимые множества. Множество может считаться аналитически определимым, если его можно определить как множество значений одного из многих переменных, связанных несколькими равенствами и неравенствами, в которые входят функции этих переменных, аналитически представимые, т. е. функции многих переменных, входящие в классификацию Бэра. Одним из простейших типов после В-множеств являются так называемые А-множества (М. Я. Суслин и В. Н. Лузин), которые можно определить как множества значений счетно-разрывной функции для значений х в каком-либо промежутке. Если у = f(х) есть такая функция, то множество рассматриваемого типа есть множество точек на оси у, получаемое проектированием на ось у точек кривой у = f (х), соответствующих точкам некоторого отрезка на оси х.

Обратимся к рассмотрению в пределах общей теории функций основных операций анализа бесконечно малых: дифференцирования и интегрирования.

Производная функции, f(х), как известно, определяется как предел для h = 0 отношения

Одно время полагали, что для всякой непрерывной функции этот предел существует. Вейерштрассе построил пример непрерывной функции которая ни для какого значения х не имеет производной. Функция  эта определяется бесконечным рядом

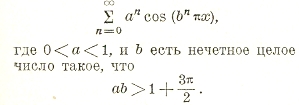
Функции  дифференцируемые, т. е. имеющие производную для всех значений переменного, за исключением, может быть, отдельных исключительных, являются частным подклассом в классе непрерывных функций.

Обратимся к рассмотрению отношений r(х,h) в самых общих предположениях. Для данного значения х отношение r (x, h) есть функции аргумента h. Предположение существования предела r (x, h) для h = 0 эквивалентно требованию, чтобы точка h = 0 была точкой непрерывности для функций r(х,h). Вообще говоря, этого, конечно, не будет, и для h = 0 будут иметь место все те возможности, которые выше были рассмотрены в точке разрыва функций. Для r(х,h) можно, согласно предыдущему, в точке h = 0 рассматривать 4 количества: верхнюю и нижнюю грань справа и верхнюю и нижнюю грань слева. Эти 4 количества соответственно называются верхним и нижним правыми, верхними нижним левыми производными числами функций f(x) в точке x (производные числа Dini); их иногда обозначают следующим образом:

Числа эти могут быть конечными или же могут равняться +∞ или —∞.

Если равны два правых производных числа, то существует предел отношения r(х,h) для положительных значений h, равный общей величине D⁺f(х) = D₊ f(x); этот предел называется правой производной функций f(x). Равным образом, если D^-f(х)=D_f(х), то эта общая величина называется левой производной. Обычная производная существует, если все четыре производных числа совпадают между собой, и тогда

Заданием в данном промежутке своей производной функции, как известно, определяется в этом промежутке до произвольного постоянного. Как обстоит дело, если задано одно из производных чисел? Если это производное число везде конечно, за исключением, может быть, счетного множества точек, то функция тоже определяется до произвольного постоянного. В других случаях функция может и не вполне определяться, т. е. могут существовать существенно различные функции с одним и тем же производным числом.

Классическое определение интеграла применимо к непрерывным функциям и к довольно узкому классу разрывных. Лебег дал новое определение интеграла, применимое к гораздо более широкому классу функций.

Пусть f(x) измеримая, ограниченная функця, данная в промежутке [а, b]. Пусть L и I верхняя и нижняя грани значений f(х) в [а, b]. Разобьем промежуток [L, I] на частичные, вводя промежуточные значения

Рассмотрим множество значений x, для которых f (х) содержится между двумя соседними l_k и введем обозначение для меры такого множества:

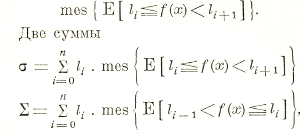
как нетрудно доказать, стремятся к общему пределу, независимо от закона разбиения промежутка [L, l] лишь бы разности l_i – l_i-1 стремились к нулю, и этот общий предел и есть интеграл Лебега функций f(х), обозначаемый, как и классический интеграл,

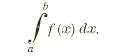
Таким образом, всякая ограниченная измеримая функция интегрируема по Лебегу или, как иногда говорят, суммируема. Если функция f(х) не ограничена, то заменяем ее функцией f_M(х), которая совпадает с f(х) везде, где |f(х)|< М и равна ± М везде, где |f(х)|≥М. функция  f_M (х) ограничена и, следовательно, суммируема. Ее интеграл Лебега в пределах от а до b есть функция М; если существует его предел для М = ∞, то этот предел и считаем интегралом Лебега данной функции f (ч) от а до b. Таким образом, из класса измеримых функций выделяется подкласс функций суммируемых, включающий в себя все ограниченные функции, но содержащий и неограниченные.

Если функция f(х) интегрируема в классическом смысле, то ее интеграл Лебега совпадает с классическим интегралом этой же функции. Интеграл Лебега обладает всеми основными свойствами классического интеграла.

Интеграл Лебега с переменным верхним пределом

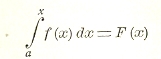
есть непрерывная функция х с ограниченным изменением. Мало этого, можно доказать, что F (х) есть функций абсолютно непрерывная, т. е. что если мы возьмем конечное или счетное множество каких-либо отрезков внутри области определения F (х), то сумма колебаний F (х) в этих отрезках стремится к нулю вместе о суммой длин этих отрезков, и это свойство есть характеристичное для неопределенного интеграла Лебега.

Функция  F(х), как показал Лебег, имеет почти всюду (т. е. за исключением множества меры нуль) производную, равную f(х). Таким образом, интеграл Лебега решает задачу нахождения примитивной для данной суммируемой функции f(х), т. е. задачу нахождения функции F(х), производная которой равна f(х):

причем это равенство имеет, вообще говоря, место только «почти всюду».

Существуют и дальнейшие обобщения определения интеграла, из которых следует отметить интеграл Данжуа (Denjoy), решающие задачу для несколько более широкого класса функций. Если же отказаться от требования дать регулярный процесс для определения примитивной, то эта задача сама па себе в наиболее общем виде решается (Н. Н. Лузин) для любой измеримой функции, почти всюду конечной, и притом существует бесчисленное множество существенно различных (отличающихся не только на постоянное) непрерывных функций F(х), для которых почти всюду

Выше было упомянуто, что дифференцируемые функции являются частным подклассом класса непрерывных функций. Еще более частное семейство функций получим, предположив существование производных сколь угодно высокого порядка. Для такой функции имеет место для любого значения х (за исключением тех, для которых нарушаются наши предположения) разложение в конечный ряд Тэйлора:

Предположив, наконец, что предел остаточного члена равен нулю для n→∞, приходим к классу так называемых аналитических функций, для которых в области любого значения х (может быть за исключением некоторых отдельных значений) имеет место разложение в бесконечный ряд Тэйлора

Вопрос о сходимости степенного ряда (А) естественным образом приводит к необходимости рассмотрения не только действительных, но и комплексных значений переменного. Так, разложение по степеням х функции  1/(1+x²) оказывается сходящимся только внутри отрезка (—1, +1), хотя точки — 1 и +1 ничем особенным не выделяются по отношению к рассматриваемой функции. Дело становится ясным из рассмотрения функции 1/(1+x²) для комплексных значений х: функция эта имеет особые точки х=±√—1, и ряд по степеням х сходится внутри круга с центром в начале, окружность которого проходит через упомянутые точки. Результаты, полученные в этом направлении Коши (Cauchy), в значительной мере послужили основанием для создания общей теории аналитических функций комплексного аргумента.

В основе этой теории лежит известное геометрическое изображение мнимого количества z = x + іу точкой (x, у) плоскости с прямоугольными Декартовыми координатами x, у. Каждому значению z соответствует точка плоскости и обратно; кроме того, мыслится одна идеальная «бесконечно удаленная» точка, соответствующая значению z = ∞. На плоскости мнимого переменного приходится рассматривать линии, причем непрерывной линией (в смысле Жордана) называется геометрическое место точек, определяемых двумя уравнениями х = φ(t), у = ψ(t), где φ и ψ две однозначных непрерывных функции действительного параметра t. Дальнейшее ограничение вносится требованием, чтобы линия не имела кратных точек, для чего налагается требование, чтобы соответствие между значениями t и точками линии было взаимно-однозначное. Линии, с которыми чаще всего приходится иметь дело в теории аналитических функций, предполагаются, кроме того, имеющими длину; другими словами, для всякой дуги такой линии периметры вписанных многоугольников стремятся к пределу при увеличении числа сторон, для чего достаточно потребовать ограниченности этих периметров. Таковые линии называются спрямляемыми.

Областью в плоскости называется множество связное и состоящее исключительно из внутренних точек; другими словами: 1° каждые две точки области могут быть соединены ломаной линией, целиком принадлежащей к области; 2° около каждой точки области, как около центра, можно описать круг, все точки которого суть точки области. Границей области называют множество точек, которые одновременно являются предельными для точек, принадлежащих и не принадлежащих к области (внешних точек). Граница области может быть весьма сложной структуры. В частности она может состоять из одной или нескольких Жордановых замкнутых линий. По теореме Жордана обратно можно утверждать, что всякая замкнутая, простая (без кратных точек) Жорданова линия ограничивает область. Окрестностью точки z₀ = х₀ + іу₀ называют какую-либо область, содержащую точку z₀ и все точки z которой отстоят от z₀ меньше известного предела h : |z — z₀| < h. В частности можно описать около z₀ окружность радиуса h.

На ряду с переменным z = х + iy рассмотрим переменное w = u + іv.

Если каждому значению z соответствует определенное значение w, то можно сказать, что w есть функция z и обозначать w = f(z); при этом между плоскостями х, у и w, v этих переменных устанавливается соответствие, в силу которого каждой точке (x, у) первой плоскости соответствует определенная точка (u, v) второй. В таком общем виде определение функций, однако, не представляет самостоятельного интереса: в самом деле, ясно, что каждая из координат u,v является функцией х и у, и обратно — всякая пара функций u, v двух действительных переменных х, у дает функцию w = u + іv переменного z = х + iy в том общем смысле, какой установлен выше. Для того, чтобы иметь в собственном смысле функцию комплексного переменного r, следует ввести ограничение, к которому придем, рассматривая отношение

Пусть точка z₀ + Δz по какому-либо пути стремится к точке z₀ (и следовательно модуль Δz стремится к нулю).

Вообще говоря, отношение Δw/Δz может при этом стремиться к различным пределам в зависимости от пути точки z₀ + Δz. Потребуем в частности, чтобы упомянутое отношение стремилось к одному вполне определенному пределу, независимо от пути точки z₀ + Δz. В таком случае будем говорить, что функция f (z) имеет в точке z₀ производную f' (z₀). функция f(z), определенная в некоторой области Т (в частности — во всей плоскости), называется аналитической в Т, если она в Т однозначна (т. е. в каждой точке области Т имеет одно значение) и в каждой точке Т имеет производную f (z). Функция  f(z) называется аналитической в точке z₀, если она аналитическая в окрестности z₀.

Требование существования производной f'(z) в области Т, при допущении дифференцируемости функций u,v, приводит к так называемым уравнениям Коши-Римана:

Обратно, если имеем две однозначных функций u,v  переменных х, у, удовлетворяющие уравнениям (В), то они определяют аналитическую функцию w = u + іv комплексного переменного z = х + iy. Каждая из функций u, v в отдельности удовлетворяет уравнению Лапласа:

Обратно, имея решение u(х,у) уравнения (С), из соотношений (В) квадратурами находим «сопряженную» функцию v (определяемую до произвольного постоянного) и, следовательно, функцию комплексного переменного w = u + іv. Таким образом, устанавливается тесная связь между аналитическими функциями комплексного переменного z и функцией двух действительных переменных х, у, удовлетворяющими уравнению Лапласа (С) — так называемыми «гармоническими» функциями.

Если имеем функцию w = f(z) аналитическую в точке z₀ и если f’(z₀) отлична от нуля, то соответствие, устанавливаемое функцией f(z) между плоскостями переменных z и w, таково, что окрестность точки z₀ непрерывно и взаимно однозначно отображается на окрестность точки w₀ = f(z₀) и притом любые две линии, проходящие через точку z₀ на  плоскости z, отображаются на плоскости w двумя линиями, пересекающимися в точке w₀ под тем же углом. Если f (z) — аналитическая функция в некоторой области Т, и если везде внутри этой области f(z) отлична от нуля, то области Т соответствует на плоскости w некоторая область Т, причем соответствие это взаимно  однозначное, непрерывное и с сохранением углов; отсюда следует также и сохранение подобия в бесконечно малых частях. Такое соответствие называется конформным, и функця w = f(z), таким образом, конформно отображает область Т плоскости z на область Т’ плоскости w. Обратно, конформное соответствие двух областей всегда осуществляется некоторой аналитической функцией.

Задача конформного отображения одной области на другую может быть, путем введения третьего комплексного  переменного, сведена к задаче конформного преобразования данной области Т на круг (или на полуплоскость). Область Т предполагается односвязной, т. е. граница Т предполагается образующей одно непрерывное связное множество.

Задача состоит в изыскании аналитической функции f (z), осуществляющей конформное преобразование области Т на внутренность круга и устанавливающей взаимно  однозначное соответствие между границей Т и окружностью круга. В такой форме задача сначала решалась для более или менее частных случаев; Каратеодори (Саrаtheodory) решил ее для области, ограниченной любой простой замкнутой Жордановой линией. Случай наиболее общей односвязной области потребовал детального исследования структуры границы области, и это исследование тоже было выполнено Каратеодори.

Определение аналитической функции, данное выше, предполагает заранее данную область. Для того, чтобы получить окончательное общее определение, необходимо ввести понятие аналитического продолжения. Пусть дана функция f (z) аналитическая в  области Т. Пусть имеется область Ť, граничащая с областью Т по линии С. Если возможно для точек области Ť и линии С построить такие значения φ (z) и W, что совокупность значений f (z), φ (2), W образует одну функцию аналитическую в области, образуемой совокупностью областей Т, Ť и линии С, то φ (z) и W называются аналитическим продолжением f (z) в область Ť.

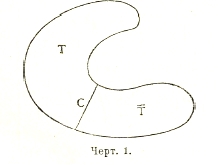
Черт. 1.

В основе понятия аналитического продолжения лежит теорема «единственности», которая может быть формулирована так: функция аналитическая в данной области и исчезающая для точек множества, имеющего хотя одну предельную точку внутри области (например, на дуге кривой, лежащей внутри области), тожественно равна нулю в области. Отсюда следует, что две аналитические функции, совпадающие в точках множества, имеющего хотя одну предельную точку внутри области, совпадают во всей области. Теорема единственности в известной мере, при некоторых ограничениях, распространяется на случай множества, лежащего на границе области.

Возвращаясь к определению аналитической функции, предположим, что нам дана функция f(z), аналитическая внутри данной области Т. Строим возможные ее аналитические продолжения в примыкающие области Ť; получаем аналитическую функцию, определенную в более широкой области. Продолжаем этот процесс и определим, в конце концов, аналитическую функцию как совокупность f(z) и всех получаемых продолжений. При  этом в процессе всего построения, в силу теоремы единственности, не может быть нескольких различных продолжений через одну и ту же линию С. Окончательно полученная нами область SE может или состоять из всей плоскости с выключением того или иного множества точек, недостижимых в процессе продолжения и называемых особыми точками функции, или же область Æ есть область ограниченная (например, внутренняя область замкнутой Жордановой кривой), и тогда имеем функций с так называемой естественной границей, за которую она не может быть аналитически продолжена; может быть и так, что функция определена вне некоторой ограниченной области, внутрь которой она не может быть продолжена. Примером функции с естественной границей может служить функция, определяемая рядом

1 + 2q + 2q⁴ + 2q⁹ +…,

для которой естественной границей служит окружность круга радиуса = 1 с центром в начале.

При всевозможных аналитических продолжениях первоначально данной функций мы можем получать перекрывающиеся области (например, область Ť может частично перекрываться с Т; см. черт. 2). Если при этом во всякой точке области определения функции Æ получается только одно значение, то функция называется однозначной, в противном случае — многозначной.

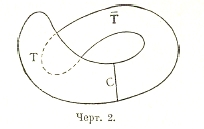
Черт. 2

Весьма важную роль в теории аналитических функций играет операция интегрирования по контуру. Пусть имеем аналитическую функцию f(z) и дугу спрямляемой линии («контур») С внутри области Т, в которой дана функций f(z). На линии С берем последовательность точек z₁, z₂, ..., z_k, ..., z_n, причем z₁ и z_n, совпадают с началом и концом дуги С. Сумма

стремится к определенному пределу при увеличении числа точек z_k, если только каждая из разностей z_i+1—z_i при этом стремится к нулю. Предел этот называется интегралом f(z) по контуру С и обозначается:

Основной теоремой теории является так называемая теорема Коши: «Если функциz f (z) —аналитическая везде в области Т (а следовательно и однозначная) и если внутри этой области имеем замкнутую спрямляемую линию С, то интеграл взятый по этой линии равен нулю»:

Линия С ограничивает некоторую область, лежащую внутри области Т.

 Черт. 3.

В окрестности любой точки внутри С функция f (z) по предположению — аналитическая. Теорема верна и для многосвязной области, ограниченной несколькими линиями С₁, С₂, . . С_n (см. черт. 3).

Если функция f (z) — аналитическая в области любой точки внутри контура С, за исключением нескольких отдельных точек, и однозначна внутри С, то

где C_i — контур, описанный около особой точки z_i, например окружность круга, имеющего z_i своим центром. Интеграл

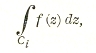
очевидно, не зависит от радиуса этого круга и называется интегральным вычетом для точки z_i.

Из теоремы Коши следует так называемая формула Коши: если точка z лежит внутри области Т, в которой функция f(z) — аналитическая, то

 

где С — линия, ограничивающая область Т. Отсюда простым дифференцированием по z получается

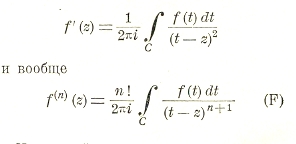
Из этих формул следует, что аналитическая функция имеет производные любого порядка и что все они тоже аналитические функции.

Из формулы Коши (Е) легко получается разложение аналитической функций в ряд Тэйлора:

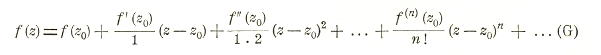
Ряд этот сходится равномерно внутри круга с центром в точке z₀, внутри которого функция f (z) — аналитическая. Наибольший возможный круг получим, описывая из z₀ , как из центра, окружность, проходящую через ближайшую к z₀ особую точку функции f(z).

Вейерштрасс пошел обратным путем. Аналитическая функция определяется, согласно его теории, данным степенным рядом

и всеми его продолжениями, причем под продолжениям разумеются степенные ряды, идущие по степеням разностей (z—z₀), где z₀ — точка, лежащая внутри круга сходимости одного из «продолжаемых» рядов. Продолжить функций вдоль пути L значит построить ряд кругов, имеющих центры на L, причем центр каждого следующего лежит внутри предыдущего (см. черт. 4), и круги эти служат кругами сходимости соответствующих степенных рядов. Коэффициенты каждого следующего ряда могут быть вычислены, как коэффициенты ряда Тейлора, по данному предшествующему ряду. Аналитическая функция, таким образом, определяется счетным множеством а₀, а₁, а₂,. . . коэффициентов первоначально данного степенного ряда. Этот ряд вместе со всеми степенными рядами — его продолжениями, дает полное определение аналитической функции, а область, покрытая всеми кругами сходимости, есть область определения функций. Точка, которая может быть сделана центром одного из кругов, есть обыкновенная точка; особые точки — это точки границы области определения, недостижимые «продолжением». Если, исходя из произвольной точки z и продолжая функцию по любому пути, приходящему обратно в z, возвращаемся всегда с первоначальным значением, то функция — однозначная, в противном случае — многозначная.

Черт. 4.

Если внутри некоторой области все точки — обыкновенные, то функция внутри этой области необходимо однозначная. Это следует из того, что при продолжении функции по пути, выходящему из точки z и возвращающемуся в ту же точку, мы приходим в z с прежним значением, если внутри области, ограниченной упомянутым замкнутым путем, нет особых точек функции. Могут быть и особые точки, при обходе которых мы возвращаемся с прежним значением; в окрестности такой особой точки функция однозначна. Функции, однозначные во всей области определения, могут иметь только такие особые точки. Особая точка, в достаточно малой окрестности которой нет других особых точек, называется изолированной. Если функция в окрестности точки z₀ однозначна и везде, кроме точки z₀, — аналитическая, а сверх того во всей окрестности ограничена по абсолютной величине (по модулю), то можно доказать, что она аналитическая и в z₀, т. е. что z₀ — обыкновенная точка. Пусть теперь z₀ — особая изолированная точка однозначной функции. В таком случае, согласно предыдущему, в окрестности этой точки функция f(z) не может быть ограниченной. Рассмотрим обратную величину f(z)

Везде в окрестности z₀ φ(z) — аналитическая функция; если для φ(z) и z₀ обыкновенная точка, то необходимо

следовательно при разложении в ряд Тейлора по степеням z — z₀ необходимо а₀ = 0; пусть вообще а₀=а₁ — а₂. . . = a_n-1 = 0 и а_n ≠ 0; тогда

где ψ (z₀) ≠ 0 и z₀ — нуль n-го порядка; а для функции f(z) имеем в z₀ так называемый полюс n-го порядка. В полюсе имеем f(z₀) = ∞ ив окрестности z₀

где χ(z) = 1/ψ(z) — функция аналитическая в z₀.

Изолированная особая точка однозначной функции, которая не есть полюс, называется существенно-особой точкой. В окрестности такой точки, как показал Вейерштрасс, функция сколь угодно близко подходит к любому значению. Из формулы Коши легко получается разложение функции в окрестности существенно-особой точки в ряд Лорана (Laurent)

Если членов с отрицательными степенями конечное число, то точка z₀ есть полюс.

Можно расширить определение существенно-особой точки, допустив в окрестности ее существование полюсов. Относительно поведения функции вблизи такой точки имеет место теорема Пикара: в окрестности существенно-особой точки функций принимает всевозможные значения за исключением, самое большее, двух. Можно говорить о поведении функции и в области точки z = ∞. Для суждения об этом совершаем преобразование

И функции φ(z’)=f(1/z’) исследуем в окрестности z' = 0. В этом смысле говорят, что функция f (z) в бесконечности имеет полюс или существенно-особую точку и т. д.

Функция, которая на всей плоскости не имеет особых точек, называется целой трансцендентной функцией; она может быть представлена степенным рядом, сходящимся на всей плоскости. В точке z = ∞ такая функция вообще имеет существенно-особую точку; если, в частности, точка z = ∞ есть полюс n-го порядка, то наша функция есть многочлен n-й степени. Функция, которая на всей плоскости мнимого переменного имеет только полюсы, называется мероморфной; в бесконечности она имеет вообще существенно-особую точку. Мероморфная функция может быть представлена отношением двух целых трансцендентных функций. Если точка z = ∞ в частности есть полюс или обыкновенная точка, то число полюсов на всей плоскости необходимо конечно,  и функция есть рациональная функций.

Особые точки функции могут быть и не изолированными; в частности существуют функции с особыми линиями; примером таковых могут служить функции с естественной границей.

Можно поставить себе задачу: построить аналитическое выражение, представляющее функцию во всей области ее существования. Наиболее приближается к решению этой задачи результат Миттаг-Леффлера: соединяем любую обыкновенную точку функции со всеми ее особыми точками и продолжаем полученные прямые в бесконечность. Область,  которую получим, вырезая из плоскости бесконечные лучи, идущие от особых точек в бесконечность по продолжению выше упомянутых радиусов-векторов, называется звездой Митта-Леффлера. Функция  может быть представлена рядом многочленов, сходящимся в любой точке звезды и равномерно-сходящимся в любой области, целиком лежащей внутри звезды. Ряд многочленов вполне может быть определен по разложению функции в ряд Тейлора в окрестности исходной точки.

Этот результат Миттаг-Леффлера дает повод указать на необходимость, строго различать понятия аналитической функции и аналитического выражения. Одно и то же аналитическое выражение может в разных областях определять различные аналитические функции, и ряд  полиномов

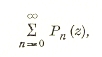
который сходится в некоторой области Т, вообще говоря, не определяет в Т одной аналитической функции. Согласно результатам Осгуда (Osgood), в любой части области Т всегда находится область, в которой ряд ∑ Р_n (z) сходится равномерно и определяет там аналитическую функцию. Вообще говоря, внутри Т существует бесчисленное множество Т₁, Т₂, T₃,... таких областей равномерной сходимости, в которых данный ряд определяет, таким образом, бесчисленное множество различных аналитических функций, не являющихся одна аналитическим продолжением какой-либо из других.

Исследование многозначных функций удобнее всего вести, пользуясь так называемыми Римановыми поверхностями. Ограничимся здесь упоминанием наиболее часто встречающегося типа особых точек многозначных функций; это — точки ветвления алгебраического характера. В окрестности такой точки функция определяется рядом вида

где q — целое положительное число. Если f(z) — алгебраическая функция, то число членов с отрицательными показателями всегда конечно. При обходе точки ветвления различные значения функции переходят одно в другое. Примером точки ветвления может служить точка z=0 для функции

Особенно разработана в настоящее время теория алгебраических функций и связанная с ней теория интегралов алгебраических функций, так называемых Абелевых интегралов. Простейшие Абелевы интегралы — это интегралы, зависящие от корня квадратного из многочлена 3-й или 4-й степени. Обращение их приводит к однозначным двоякопериодическим функциям, к так называемым эллиптическим функциям.

В общей теории многозначных функций кардинальное значение имеет результат Пуанкаре, согласно которому для всякой многозначной функции w = f(z) можно подыскать такое вспомогательное переменное t — «униформизирующее» переменное, что w и z одновременно являются однозначными аналитическими функциями t: w = φ (t), z = ψ(t). Исключение t из этих двух соотношений приводит к соотношению w = f(z). Полное и строгое доказательство результата Пуанкаре потребовало целого ряда работ (Кебе и др.), и, таким образом, создалась целая теория «униформизации».

Д. Егоров.