Фурье Жан Батист Жозеф

Фурье (Fourier), Жан Батист Жозеф, барон де, французский математик, родился, в 1768 г. в Оксерре, был сыном портного, 8 лет остался сиротой. Воспитывался в местной военной школе, находившейся в ведении монахов-бенедиктинцев, и там обратил на себя внимание выдающимися способностями. По окончании курса, однако, в армию выпущен не был вследствие бедности и недворянского происхождения, а был оставлен при школе преподавателем математики. В 1787 г. поступил послушником в монастырь, но с началом революции (1789) оставил его и вернулся в школу, где помимо математики стал читать лекции по философии, истории и другим предметам. В 1795 г.,  когда  в Париже была открыта Éсоlе Normale, Фурье по рекомендации Монжа был приглашен туда преподавателем,  а через некоторое время получил кафедру анализа в Éсоlе Politechnique.  В 1798 г. он вместе с другими учеными сопровождал Бонапарта в Египет и во время этой экспедиции, помимо научной работы (он был секретарем Египетского Института и впоследствии: принял деятельное участие в издании «Mémorial de l’expédition d’Égypte», к которому написал историческое введение), нес также различные политические и административные обязанности. По возвращении, во Францию был назначен в 1802 г. префектом Изеры и в 1808 г. возведен в баронское достоинство. В должности префекта пробыл 14 лет, после чего поселился в Париже, отдавшись всецело научной деятельности. В 1817 г. был избран членом Академии Наук, в 1822 г. — непременным секретарем (совместно с Кювье). Умер в 1830 г.

Главные научные заслуги Фурье заключаются в разложении функций в тригонометрические ряды кратной переменной, т. н. ряды Фурье, в создании математической теории теплопроводности и в исследованиях в области численного решения уравнений. В своем сообщении Академии Наук в 1807 г. Фурье показал, что любая функция f (х) вещественного переменного может быть представлена рядом вида ∑ a_n sin nx+b_n cos nx, где

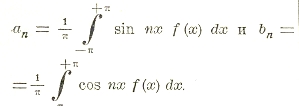
(Так, например, функция определенная в промежутке 0... π, так что для первой половины его f(х)= π/4, а для второй f(х)= — π/4, может быть представлена рядом ½  sin 2х + 1/3 sin 6х + 1/5 sin 10х ...). Этим достигалось значительное расширение самого понятия функции. Полному доказательству этого предложения вместе с точным определением условий, при которых оно имеет место, было уделено много внимания последующими математиками — Дирихле, Риманом, Вейерштрассом и др. В своем развитии учение о рядах Фурье сыграло чрезвычайно плодотворную роль для строгого установления основных понятий анализа, как-то: функция, непрерывность, дифференцируемость, интегрируемость и т. д.

Найденными рядами Фурье воспользовался при изучении теплопроводности твердых тел, первым применив средства математического анализа к учению о теплоте и тщательной и совершенной разработкой вопроса давши образец для развития других отделов математической физики. Полное изложение своих идей Фурье дал в составившем эпоху в развитии математических и физических наук и премированном Академией мемуаре «Théorіе des mouvements de la chaleur dans lescorps solides» (1812).Изданная в 1822 г. его «Théorie analytique de la chaleur» является в значительной мере повторением первой работы. Из других исследований Фурье заслуживают внимания, как уже было указано, его изыскания в области уравнений, где им дан способ отделения корней (см. II, 96). Относящиеся сюда работы были собраны и опубликованы после смерти Фурье Навье под заглавием «Analyse des équations déterminées» (1831). О значении Фурье для статистики см. XLI, ч. IV, 477. Полное собрание сочинений Фурье издано Дарбу — «Oeuvres de F.» (1889—90).

А. Ш.