Геодезия

Геодезия (от греческих слов γň — земля и δαίειν — делить), в переводе на русский язык значит землеразделение; однако, это название не исчерпывает всего содержания науки и свидетельствует лишь об историческом происхождении ее из решения тех практических вопросов, которые представлялись еще в древности при разделении подвергавшихся обработке земель между земледельцами. В настоящее время под именем геодезии разумеется наука, занимающаяся изучением и определением величины и формы земной поверхности. Общие методы этого изучения суть методы геометрии в приложении ее к тем частным задачам, которые представляются для решения на поверхности земли. Поверхность нашей планеты на две трети покрыта водой: океанами и морями и на одну треть сушей: материками и островами; поверхность океанов, если отвлечься от малых колебаний ее — волн, поверхность правильная, в то же время поверхность материков и островов в высшей степени неправильная. Задачу изучения формы земной поверхности естественно разделить на две части: во-первых, можно вообразить, что правильная поверхность океанов продолжена под континенты, и изучать эту основную форму, которая называется математической поверхностью земли, или геоидом, во-вторых, изучению будет подлежать поверхность суши, или физическая земная поверхность по отношению к указанной математической. Соответственно этому разделению задачи, геодезия делится на высшую геодезию и низшую, иначе топографию, или практическую геометрию. То же разделение геодезии на две части можно выводить и иначе: вопрос об изучении формы земной поверхности проистекает из целого ряда практических надобностей общественной жизни: военных, технических, юридических. При этом иногда дело идет об изучении формы и размеров весьма значительных пространств земной поверхности: целой страны или крупной ее части, в другой раз вопрос сводится к изучению протяжения и рельефа малого участка земной поверхности; в то время, как для разрешения первой задачи необходимо знание величины и формы геоида и требуется приложить к решению все методы современной математики, для задач второго рода достаточными являются приемы элементарной математики, и результаты изучения основной формы земли нужно знать лишь в самых общих и грубых чертах.

Неодинаковые трудности являются и при разрешении задачи, которая всегда сопутствует изучению того или иного района земной поверхности: задачи изображения района на бумаге, т. е. составления карты значительного пространства или плана малого участка. Весьма часто разделение геодезии приурочивается к такому практическому разделению задачи, причем высшей геодезией называют изучение методов съемки значительных пространств земной поверхности и составления карт, и низшей геодезии — решение геометрических вопросов, касающихся малых участков, и составление планов.

Начала геодезии теряются в глубокой древности: имеются свидетельства о том, что еще за 12 веков до Рождества Христова в  Египте уже измерялись земельные участки и сообразно с этими измерениями уплачивались земельные подати. Несомненно, что развитие геометрии было вызвано и подвинуто теми практическим и задачами, которые встречали в своей деятельности древние землемеры, и развитие геодезии тесно связано с успехами математики, астрономии и физики. Первое определение величины земли было сделано в Египте и принадлежит Эратосфену в III веке до Рождества Христова. Известны и другие попытки таких же определений в древнейшую эпоху, сделанные греками и арабами. За 200 лет до Рождества Христова появилось также и первое сочинение по практической геометрии, принадлежащее Герону из Александрии. В Риме землемеры составляли особую группу, весьма почетную, и исполняли разного рода съемки земель, как по поручению общественной власти, так и по требованиям частных лиц при покупках, мене и разделе недвижимых имуществ; они являлись также экспертами при спорах о границах владений. Развитие геодезии, как и других наук, было надолго прервано в течение веков варварства, и возрождение ее относится уже к XIII веку нашей эры, от которого дошли до нас трактаты по геометрии и совместно с ней геодезии. В XVI веке входят в употребление инструменты, являющиеся прототипами современных геодезических инструментов, а также вырабатываются постепенно методы измерения и решения различных геометрических задач. В самом начале XVII века был развит метод определения длинных линий на земной поверхности через посредство триангуляции, и голландский ученый Виллеброрд Снеллиус приложил этот метод к определению длины дуги меридиана, сделавши, таким образом, первое определение размеров земли тем приемом, которым пользуются с новыми средствами и до сего времени. К XVII веку относится также крупный шаг в деле постройки астрономических и геодезических инструментов, заключающийся в приспособлении к ним зрительных труб. В XVIII веке задача об определении размеров земли осложнилась исследованием самой фигуры земли. На грани XVII и XVIII веков Ньютон доказывал по теоретическим соображениям, что земля должна иметь форму не шара, как думали раньше, но эллипсоида вращения, сжатого по полярной оси. Отсюда вытекала задача: найти элементы земного сфероида, т. е. размеры его полуосей: полярной и экваториальной, или иначе величины экваториальной полуоси и сжатия. Работы, которые необходимо выполнить для разрешения задачи, называются градусными измерениями и приводят к нахождению длины дуги меридиана в 1°. В разных широтах эта величина имеет различное значение, и определение ее, по крайней мере, в двух местах, лежащих в широтах, возможно более различающихся, должно было дать материал для определения элементов земного сфероида. В XVIII веке было сделано немало градусных измерений, причем наиболее замечательными между ними были два градусных измерения: одно в Перу, другое в Лапландии, исполненных французами по почину Академии наук. Эти два измерения подтвердили опытным путем то предположение о фигуре земли, которое высказал впервые Ньютон. Истинный расцвет геодезических работ относится к XIX веку, когда повсюду, сперва в Европе, потом в Азии (Индии), Америке и Африке, велись крупнейшие сплошные работы для составления карт, и государственные средства щедро отпускались на этот предмет. Для обоснования съемок повсюду предпринимались большие триангуляции, из которых извлекались необходимые ряды для градусных измерений по меридианам и параллелям земного сфероида. На этих работах выяснялись и совершенствовались методы измерений, а лучшие математики дали свои решения труднейшим вопросам, встречавшимся при числовой обработке собиравшегося материала. Классические методы дали: Гаусс, руководивший градусным измерением в Ганновере (1821—1824 гг.), Бессель в провинциях Восточной Пруссии (1831—1834 гг.), Вильгельм Струве, давший описание русско-скандинавского градусного измерения, самого большого из европейских (1861 г.), английский геодезист Кларк, обработавший индийские триангуляции. Вместе с развитием методов высшей геодезии совершенствовались методы топографических съемок и инструменты, назначенные для их производства. Было бы бесполезно указывать здесь на отдельных геометров и механиков, улучшавших методы и инструменты, так как в этом прогрессе участвовало чрезвычайно много лиц, вносивших каждый свою крупинку, делавшуюся весьма быстро общим достоянием. Можно указать лишь на то, что германские механики идут впереди всех по обдуманности инструментов, тщательности их выполнения и разнообразию типов; в то же время русские геодезисты дали немало своеобразных изменений как в методах производства работ, так и в конструкции приборов. Размеры земли определялись разными учеными, как из отдельных градусных измерений, так и из той или иной группы их. Позднейшим определением, сделанным на основании всего опубликованного до 1880 г. материала, является определение Кларка, который дает следующие цифры: длина большой полуоси (экваториальный радиус) земного сфероида а=2 989 457,4 саженей (5979 верст), длина малой полуоси (полярный радиус) 6=2 979 270,7 саженей (5959 верст), отсюда величина сжатия земли, т. е. (a-b)/b = 1/293.

При изучении формы физической земной поверхности воображают, что каждая ее точка проектируется на математическую поверхность земли отвесной линией, проведенной в данной точке; при этом на поверхности геоида получается горизонтальное проложение точки физической земной поверхности; каждой линии или контуру на физической земной поверхности будет соответствовать контур горизонтального проложения на поверхности геоида. Задача изучения земной поверхности при этом распадается на две части: во-первых, нужно определить расположение горизонтальных проложений различных точек и линий и изобразить их на бумаге. Эта задача составляет предмет горизонтальной съемки и составления карты или плана. Во-вторых, нужно найти высоты точек физической земной поверхности над их горизонтальными проложениями (иначе, отметки над уровнем моря) — эта задача разрешается нивелированием, результаты коего могут быть изображены графически либо отдельно в виде профиля или разреза вертикальной плоскостью земной поверхности по той или иной линии, либо эти результаты цифровыми надписями или условными знаками показываются на планах горизонтальных съемок, тогда это будут нивелирные планы. Горизонтальные проложения контуров данного пространства физической земной поверхности располагаются всегда, очевидно, на математической поверхности земли. Если этот район невелик, а именно не превышает нескольких десятков верст, то можно считать его, благодаря значительным размерам земли, за плоскость, и задача изображения всех контуров будет весьма проста; контуры могут быть вычерчены в подобном и уменьшенном виде, и мы будем иметь план района. Если же дело идет о значительном пространстве, то кривизной земли уже нельзя пренебрегать и на плоскости, на бумаге, нельзя изобразить значительный район без неизбежных искажений. При съемках значительных пространств земной поверхности, например, при государственных съемках, прежде всего, избирают на местности систему главных опорных точек и стараются определить их относительное положение с возможной точностью. Лучшим методом для этого является метод триангуляции, или тригонометрической сети; он заключается в следующем: опорные пункты выбираются на местности так, чтобы они составляли цепи или сети последовательных треугольников; из каждого пункта должны быть видны, по крайней мере, два соседних, составляющих вместе с ним вершины треугольника. Так, на чертежах точки А, В, С составляют первый треугольник, на его стороне АС строится второй ACD, далее пойдет CDE, к сторонам которого в свою очередь примыкают СЕР и DEG, потом пойдут DGJ, JDK, KDL и LDM. Эти треугольники должны быть, возможно, ближе к равносторонним. Длины сторон триангуляции, или расстояния между пунктами, делаются сперва весьма длинными, от 20 до 30 верст, — это будет сеть первого класса; внутри этой сети размещается сеть более мелких треугольников второго класса со сторонами от 5 до 10 верст, причем эта более мелкая сеть опирается на сеть первоклассную так, что пункты последней служат непременно также и вершинами второклассной сети; таким же образом на пункты второклассной сети может опираться сеть третьего класса и т. д., покамест не получится сеть пунктов столь густая, что может служить опорой для съемки всех подробностей, которые нужно изобразить на планах в избранном масштабе.

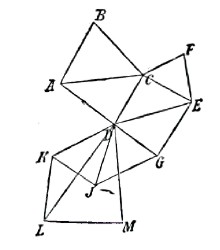
Пункты тригонометрической сети обозначаются на местности особыми знаками: высокими вехами, а еще лучше пирамидами из четырех бревен, и подземными признаками на случай разрушения надземных: каменными или кирпичными столбиками и т. п.; стараются также ввести в сеть, как вершины треугольников, хорошо видимые, прочные местные предметы, например, колокольни церквей (обыкновенно шарик под крестом служит пунктом сети). Чтобы найти относительное расположение точек сети в горизонтальном проложении их, измеряют длину одной какой-либо стороны с возможно большей точностью; эта сторона называется базисом сети; потом измеряют в каждом треугольнике все три угла, причем излишнее измерение третьего угла производится для того, чтобы можно было вполне удостовериться в отсутствии грубых ошибок при измерении углов. Углы измеряются инструментами, которые называются теодолитами. Сумма трех измеренных углов треугольника всегда вследствие неизбежных малых погрешностей измерений отличается от 180°, и по оказавшимся разницам во всех треугольниках сети можно судить, с какой точностью произведены измерения. Оказавшиеся малые погрешности распределяют между измеренными углами (эти вычисления называются уравнительными) так, чтобы повсюду сумма трех углов оказалась равной 180°, и приступают тогда к последовательному решению треугольников, начиная от примыкающих к базису. В результате получаются длины всех сторон сети. Далее следует всю сеть надлежащим образом ориентировать, для чего нужно измерить угол, составляющийся одной какой-либо стороной сети с меридианом; это определение может быть сделано из астрономических наблюдений; равным образом определяются географические широта и долгота хотя бы одного пункта. После этого для каждой вершины сети вычисляются координаты ее, т. е. широта и долгота, или же прямоугольные координаты вершин относительно условно выбранных осей, если сеть располагается на плоскости.

На основании тригонометрической сети съемка всех подробностей производится весьма удобно и быстро при помощи инструмента, называющегося мензулой (см. геодезические инструменты). На столик мензулы наклеивается бумага, на которую, прежде всего, наносят в избранном масштабе все тригонометрические пункты снимающегося пространства. Если мензулу установить в одном из тригонометрических пунктов и ориентировать доску так, чтобы изображения сторон треугольников сети сделались параллельными соответственным линиям на местности, то можно зарисовать все подробности вокруг данной точки в довольно большом районе (примерно на 100 сажен вокруг); для этого посылают рабочего с рейкой (узкой доской около сажени длины с делениями) последовательно на те точки, например, изгибы контура, которые должны быть изображены на плане, и на мензуле по линейке, направленной на рейку, прочерчивают каждый раз соответственное направление; чтобы отложить на нем далее расстояние до точки, определяют последнее при помощи дальномера. Таким образом, тут же в поле графически вырисовываются все интересующие съемщика контуры. Этот способ съемки называется полярным способом. Линейка, к которой прикреплена дальномерная труба, направляющаяся на рейки, называется кипрегелем и составляет самую существенную принадлежность мензулы. После того, как съемка вокруг данной точки тригонометрической сети сделана, с мензулой переходят на следующую точку и повторяют вокруг нее тот же прием; однако, редко сеть опорных пунктов может быть так густа, чтобы всю съемку возможно было произвести, устанавливая мензулу только на тригонометрических пунктах; необходимо бывает число станций мензулы значительно увеличить; для этого на местности разбивают сеть мелких треугольников, опирающуюся на тригонометрические пункты, изображают на мензульной доске графически эти дополнительные пункты и пользуются ими при съемке деталей так же, как и определенными тригонометрически. В России сплошные съемки велись и ведутся офицерами корпуса военных топографов; в настоящее время эти съемки сосредоточены в западной половине Европейской России, а также в Крыму и на Кавказе. Масштаб съемок полверсты или верста в одном дюйме, т. е. планы составляются с уменьшением 1:21000 или 1:42000. Оригинальные планы с мензульных досок переносятся с надлежащим уменьшением на листы карты масштаба 3 версты в дюйме (1:126000), которые и издаются для всеобщего пользования. Для съемки более мелких земельных участков в целях разграничения земельной собственности или для хозяйственных нужд имений служат следующие инструменты: для измерения углов в градусной мере — малые теодолиты и астролябии, для измерения линий — стальные ленты и цепи по 10 саженей  длиной. Лучшим способом съемки является способ обхода данного контура, например, границ имения. При этом измеряются длины, всех граничных линий и величины углов между ними. Сумма измеренных углов сомкнутого многоугольника с n сторонами должна равняться 180° (n—2), и разность между суммой измеренных углов и указанной теоретической не может превосходить весьма тесного предела допускаемых неизбежных погрешностей. Указанных данных совершенно достаточно как для построения плана, т. е. фигуры подобного многоугольника, так и для определения площади, либо путем вычисления, либо на основании плана, составленного по измеренным данным. При построении плана обыкновенно не получается сразу сомкнутая фигура, но получившаяся невязка не может превосходить известных пределов, иначе такая недопускаемая невязка свидетельствует о сделанных где-либо при измерениях линий или углов грубых ошибках и вызывает необходимость поверки произведенных измерений. Для возможности ориентирования плана относительно стран света к теодолитам весьма часто присоединяют буссоль. Съемка мелких контуров внутри границ имения производится либо теодолитом и лентой так же, как и съемка граничного полигона, либо пользуясь одной буссолью без определения углов между съемочными линиями, но с определением лишь их азимутов или румбов.

Определение превышений одних точек местности над другими и нахождение абсолютных отметок точек над уровнем моря называется нивелированием. Имеется три метода нивелирования: 1) метод непосредственного измерения разностей уровней, иначе геометрическое, или топографическое нивелирование, 2) метод геодезический, или тригонометрический, 3) физический. В первом методе всегда определяется разность уровней точек, не очень удаленных одна от другой, примерно на 50 саженей, при помощи нивелира и реек. Если две точки удалены одна от другой, то ломаную линию, их соединяющую, — ось нивелирования — разбивают промежуточными точками, пикетами, на малые отрезки, для которых и измеряют разность уровней конечных точек. Суммируя определенные таким образом разности уровней, находят разности отметок каких угодно пунктов. Путем усовершенствования инструментов при крайней осторожности и внимании к уничтожению влияния неизбежных малых погрешностей, получают результаты высокой точности. Этим методом пользуются для нивелирования оси будущей дороги, канала и проч., которое необходимо для составления проекта сооружения и производства необходимых расчетов. При геодезическом нивелировании определяют расстояние между двумя точками и измеряют также угол наклонения этой линии к горизонту.

Современные курсы и учебники геодезии: «Курс низшей геодезии», составил А. Вик, переработал и дополнил И. Иверонов, 3 тома, 1908—9 гг.; В. Витковский, «Топография» (1904 г.); «Картография» (1907 г.) и «Практическая геодезия» (1910 г.); С. Соловьев, «Курс низшей геодезии» (1908 г.); В. Бауман, «Курс маркшейдерского искусства» (1905 г.); Ф. Слудский, «Лекции по высшей геодезии» (1894 г.); Н. Цингер, «Курс высшей геодезии» (1898 г.); А. Кларк, «Геодезия» (пер. В. Витковский, 1890 г.); А. Вик, «Учебник низшей геодезии» (дополнил и вновь редактировал И. Иверонов, 1909); С. Соловьев, «Сокращенный курс низшей геодезии» (1909); «Практика низшей геодезии», составили Виноградов, Орлов, Смиренкин и Шеляпин (1911 г.).

И. Иверонов.

Геодезические инструменты, их устройство и виды.

Геодезическими инструментами называются инструменты для производства разного рода съемок; они разделяются на следующие группы: 1) инструменты для измерения длин линий, 2) экеры, 3) буссоли, 4) инструменты для измерения углов, 5) инструменты для графических съемок, 6) инструменты для нивелирных работ.

Главнейшие инструменты, принадлежащие к перечисленным группам, следующие.

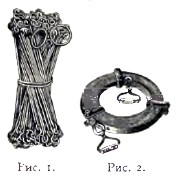
1) Для измерения линий служат: а) стальная цепь (рис. 1) в 10 сажен длины, состоящая из ста колен по 0,1 саженей каждое; б) стальная лента (рис. 2), длиной так же в 10 саженей и шириной около дюйма, с метками через одну десятую сажени и с нумерацией последовательных саженей; лента вытесняет в настоящее время на практике цепь; в) за границей для измерения линий пользуются пятиметровыми деревянными брусьями. Вспомогательным инструментом, необходимым для определения угла наклонения к горизонту измеряемых линий или для нахождения приведения измеренной линии к горизонту, служат эклиметры разных типов. Перечисленными инструментами линии измеряются со случайными ошибками, составляющими от 1/1000  до 1/10000 от длины линии в зависимости от условий измерения.

Для более тонкого измерения линий, необходимого для определения, например, длины базиса тригонометрической сети, служат особые приборы, иногда довольно сложные, называющиеся базисными приборами.

2) Под названием экер разумеется прибор для разбивки на местности постоянных, чаще всего прямых углов. Экеры бывают простые и отражательные; из них последние в свою очередь разделяются на зеркальные и призменные. Простые экеры бывают; крестообразный, восьмигранный, цилиндрический, конический, шарообразный. Экер крестообразный состоит из двух металлических линеек, соединенных между собой под прямым углом. На концах линеек помещены диоптры, визирные плоскости которых составляют между собой угол в 90°.

Снизу линеек в месте их соединения приделывается втулка, которой экер надевается на штатив или на палку. Восьмигранный экер (рис. 3) состоит из медной восьмигранной призмы, на средине каждой грани которой сделан диоптр, и визирные плоскости диоптров пересекаются между собой, составляя углы не только в 90°, но также в 45° и 135°. Экеры других форм отличаются только тем, что визирные прорезы в них сделаны на поверхностях цилиндра, конуса, шара.

Из зеркальных экеров наиболее распространен двузеркальный (рис. 4); он состоит из металлической коробки, к двум стенкам которой под углом в 45° прикреплены зеркала. Над зеркалами имеются в стенках коробки окна, так что, смотря на внутреннюю стенку коробки, мы видим отражение вехи, поставленной в стороне, куда обращен раструб зеркал, а над ним чрез окошко — веху, поставленную прямо пред наблюдателем. Если отражение вехи в зеркале кажется продолжением вехи,   прямо видимой, то мы находимся в вершине прямого угла, стороны которого проходят чрез упомянутые две вехи. Зеркала могут быть заменены призмами: одной прямоугольной равнобедренной призмой, двумя призмами, пятисторонней призмой.

3) Буссоль служит для определения углов, образованных магнитной стрелкой и данной линией на земной поверхности. Буссоли делаются с диоптрами или с трубой для визирования. Верхняя часть буссоли с диоптрами (рис. 5) состоит из медной линейки с диоптрами, на средине которой приделано кольцо с градусными делениями. В центре кольца на остром шпиле подвешивается магнитная стрелка.

К линейке приделывается втулка, которой буссоль надевается на баксу, в свою очередь, прикрепляющуюся к штативу. Угол между магнитной стрелкой и данной линией называется магнитным азимутом; он считается от северного конца стрелки вправо до данной линии и может иметь все значения от 0 до 360°. Если же брать между магнитной стрелкой и данной линией угол, меньший 90°, и отмечать квадрант, в который направляется линия, т. е. северо-восток (СВ), юго-восток (ЮВ), юго-запад (ЮЗ) и северо-запад (СЗ), то этот угол называют магнитным румбом. Буссоли устраиваются либо с азимутальным, либо с румбическим кольцом. В первом из них деления назначаются в одну сторону (против часовой стрелки) от 0 до 360°, и по направлению диоптров располагается диаметр, соединяющий 0° и 180°; во втором по тому же направлению устанавливается диаметр, имеющий на обоих концах нули градусов, от которых идут в обе стороны деления до 90°. Вдоль линии направляются диоптры буссоли, и тогда концы стрелки указывают величину азимута или румба линии.

4) Для измерения углов между линиями в горизонтальной плоскости служат инструменты весьма разнообразных конструкций и размеров. Наиболее важным инструментом является теодолит. Измерение углов есть основное геодезическое действие как при определении опорных пунктов для съемки при помощи тригонометрической сети, так и при собственно съемочных работах. Теодолиты для тех и других работ устраиваются по одному и тому же плану, но отличаются размерами, устройством деталей, оптической силой труб и т. п. конструктивными особенностями. Теодолиты для основных работ называются большими, для съемочных — малыми. Главные части теодолита (рис. 6) суть: 1) лимб, на котором нанесены деления и производится определение величины измеряющихся углов, 2) уровень для приведения лимба в горизонтальную плоскость, 3) вращающийся на оси в центре лимба алидадный круг с прикрепленной к нему на стойках зрительной трубой и с приборами для отсчитывания делений лимба. Эти последние приборы бывают двух типов: более простые — нониусы и более сложные и тонкие — микроскопы со шкалами или с микрометрами. Лимб соединен с подставкой, которая на трех винтах устанавливается на головке штатива и прикрепляется к нему накрепко винтом, носящим название станового винта. При измерении угла труба теодолита располагается сперва го направлению одной стороны (причем отмечается отсчетом на лимбе по  нониусу или микроскопу положение алидадного круга), потом по направлению другой стороны с новым отсчетом. Разность отсчетов дает величину угла.

Малые теодолиты разделяются на две главных системы: простые и повторительные. Существенное отличие первых от вторых состоит в том, что в простых теодолитах лимб и подставка отливаются из одного куска металла и, следовательно, когда подставка прикреплена к штативу, лимб является неподвижным; в повторительных теодолитах лимб сам вращается около оси, проходящей внутри подставки, и потому при подставке, скрепленной со штативом, лимб может вращаться, и закрепление его производится особым винтом. Это обстоятельство дает возможность измерять один и тот же угол несколько раз на новых местах лимба, этим достигаются контроль и улучшение измерений.

Второе существенное различие в конструкции малых теодолитов состоит в том, снабжен ли теодолит буссолью или нет; присоединение к теодолиту буссоли является весьма ценным на работах в России, так как все планы русских межеваний ориентировались по магнитной стрелке.

Наконец, третье существенное конструктивное отличие разных теодолитов состоит в устройстве вертикального круга для измерения углов наклонения линий; инструмент может вовсе не иметь такового, может быть снабжен сравнительно грубым сектором или вертикальным кругом (иногда с делениями, не полными, а лишь на части — секторе в 60°—90°); назначение этой части инструмента в таком случае — давать углы наклонения линий с точностью, достаточной для вычисления горизонтальных проложений измеренных линий; наконец, вертикальный круг может быть той же точности, что и горизонтальный, и предназначаться для определения углов наклонения в целях определения разности уровней; этого рода теодолиты называются тахеометрическими.

Согласно с указанным, малые теодолиты распределяются на следующие типы: 1) теодолиты простые: а) без буссоли и вертикального круга, б) с буссолью, но без вертикального круга или наоборот, в) с буссолью и вертикальным кругом; 2) теодолиты повторительные с теми же подразделениями (на рисунке 6 — теодолит повторительный с буссолью и вертикальным кругом, употребляющийся на межевых работах в России).

Трубы малых теодолитов весьма часто снабжаются сеткой нитей, рассчитанной для определения по рейке расстояний; это приспособление в трубах называется дальномером. На лимбах делаются деления обыкновенно через полградуса, и по нониусам отсчеты производятся с точностью до 1'.

Теодолиты в настоящее время вытесняют прежние инструменты того же типа и назначения, которые называются астролябиями.

Это самый старинный геодезический инструмент, изображение и описание которого встречается в древнейших трактатах по практической геометрии. В XVIII веке астролябия приобретает уже тот внешний облик, который, с позднейшими улучшениями и усовершенствованиями, она имеет и в настоящее время. Сперва астролябии (рис. 7) снабжались диоптрами, из которых два привинчиваются к лимбу и называются неподвижными, а два ставятся на алидаду, вращающуюся в центре лимба, к которой прикреплена также буссоль.

При измерении угла нужно направить неподвижные диоптры по одной его стороне, подвижные по другой, и угол между плоскостями, определяемыми этими двумя парами диоптров, выражается отсчетом по лимбу. Астролябия с диоптрами скрепляется со штативом при помощи соединительной баксы, весьма грубого приспособления, дающего возможность, однако, устанавливать лимб в горизонтальном положении. Астролябия с диоптрами описанного типа была тем инструментом, которым сделаны были с шестидесятых годов XVIII века до половины следующего крупнейшие работы по разграничению поземельной собственности в России, именно, генеральное межевание. Постепенно астролябии с диоптрами стали заменяться усовершенствованным инструментом — астролябией с трубой, сперва также на баксе, потом с  подставкой на трех винтах, устанавливающеюся на штативе. Отсюда был уже только один шаг до теодолита.

Наконец, весьма распространенным и до сего времени является сравнительно грубый угломерный инструмент, называющийся пантометром или гониометром (рис. 8).

Этот инструмент состоит из двух полых цилиндров, диаметром от 3 до 4 дюймов, стоящих один на другом, причем по верхней окружности нижнего цилиндра намечены деления лимба, а на соприкасающейся с ним окружности верхнего — нониусы для отсчетов. Нижний цилиндр скреплен с подставкой, а верхний, вращающийся, несет на себе трубу или же имеет прорезы диоптров; к нему же прикрепляется буссоль.

Для измерения углов треугольников тригонометрической сети употребляются более совершенные угломерные инструменты: большие теодолиты, чаще всего повторительные, и универсальные инструменты (рис. 9), имеющие, кроме горизонтального лимба, той же точности лимб вертикальный.

Эти инструменты имеют те же составные части, что и малые теодолиты, но изготовляются еще более тщательно, имеют большую плавность и равномерность движений различных частей. Точность, с которой измеряются углы этими инструментами, значительно выше той, которая достигается малыми теодолитами. Для этой цели в больших теодолитах и универсальных инструментах их лимбы подразделяются на более мелкие деления, например, через 10' или чаще, и в них устраиваются более тонкие приборы для отсчитывания, при помощи которых отсчеты производятся с точностью до 10” и меньше.

5) Инструменты для графического построения углов называются мензулами и служат для непосредственного изображения в поле плана снимаемой местности.

Всякая мензула (рис. 10) состоит из трех частей: а) доски, на которую наклеивается бумага для получения графического изображения контуров, б) штатива, которым инструмент ставится на землю, и в) подставки, которая служит для соединения доски со штативом. Мензулы различных систем различаются между собой именно устройством подставки.

Мензула, как и астролябия, так же весьма старинный инструмент; им уже пользовались в XVIII веке, и самое устройство мензулы того времени близко к простейшим из современных типов. Мензульная доска, или планшет, имеет форму квадрата со стороной около 20 дюймов. При съемке доска должна устанавливаться в горизонтальном положении, для чего подставку снабжают подъемными винтами, а на доску ставят уровень.

Необходимым для каждой мензулы вспомогательным прибором являются алидада или кипрегель. Алидадой (на рис. 10) называется медная линейка со скошенными ребрами и находящимися на концах диоптрами; длиной она почти равна стороне мензульной доски. Алидада приставляется на мензуле к той точке на доске, которая соответствует пункту стояния с мензулой, и направляется на те пункты, между которыми на мензуле должны быть изображены углы; по краю линейки при этом прочерчиваются стороны углов. Вместо диоптров утверждают на линейке на особой колонке зрительную трубу и получают кипрегель (рис. 11). Трубу последнего снабжают дальномером для определения расстояний и вертикальным кругом для измерения углов наклонений; такой тахеометрический кипрегель служит для совместной горизонтальной и вертикальной съемки на мензуле. Мелкими и второстепенными принадлежностями при мензульной съемке являются буссоль для ориентирования края доски по меридиану и  вилка для точной установки мензулы определенной на планшете точкой под пунктом местности (оба эти предмета видны на рис. 10).

6) Непосредственное измерение разностей высот различных точек земной поверхности производится при помощи нивелира и реек.

Принцип устройства нивелира заключается в следующем: к подставке (рис. 12), устанавливающейся на штативе, прикрепляется зрительная труба так, чтобы ось ее легко было приводить по данному направлению в горизонтальное положение; с трубой или с подставкой (как на рис. 12) скрепляется уровень, ось которого должна быть параллельна оси трубы. На точках, разность уровней коих определяется, ставятся рейки (рис. 13) — тонкие бруски, вышиной от 1 до 2 сажен с делениями на них через каждую сотку сажени (а иногда через две тысячных). Нивелир устанавливают между рейками, направляют трубу поочередно на ту и другую рейку и считают числа делений от низа реек до горизонтального луча зрения нивелира; разность этих чисел (взглядов) дает разность высот нивелируемых точек. Последовательным приложением этого приема нивелируются какие угодно длинные линии. Нивелирование производится также при помощи тахеометрического теодолита или кипрегеля, причем определяются: при помощи дальномера длина линии от инструмента до какой-либо точки местности и измеряется угол наклонения этой линии, отсюда легко вычислить разность уровней.

В последнее время начинают входить в употребление такие инструменты, в которых отсчет угла наклонения линии заменяется прямо отсчетом разности уровней; для этого к инструменту приспосабливается соответственная система счетных линеек (В',СС'). Такие теодолиты, в которых измерения углов наклонения заменяются определением разности уровней, дают возможность, следовательно, вести весьма быстро подробную съемку, как горизонтальную, так и вертикальную, с определением углов между линиями, длин линий и превышений одних точек местности над другими. Эти инструменты называются автоматическими тахеометрами. Вид одного из них, тахеометра Вагнер-Феннеля, изображен на рис. 14.

Третий способ нивелирования основан на том обстоятельстве, что давление воздуха изменяется при поднятии над поверхностью земли; вследствие этого о разности уровней точек земной поверхности можно судить по разности отсчетов барометра при одном и том же состоянии атмосферы. Таким образом, барометр является геодезическим инструментом, и в частности пружинные барометры, или анероиды, благодаря своим малым размерам и удобству переноски, являются весьма простыми и удобными нивелирными инструментами; некоторые анероиды устраиваются таким образом, что на их шкалах отсчитывают не давления воздуха в дюймах или миллиметрах, а прямо высоты точек над уровнем моря в саженях или метрах.

Построение планов производится при помощи разных чертежных инструментов, из которых следует упомянуть: линейку, треугольник, циркуль, транспортир для построения углов с масштабом. Весьма разнообразный класс инструментов составляют планиметры, которые служат для определения площадей по планам. Из них особенно распространен полярный планиметр Амслера, усовершенствованный Коради (рис. 15). Для перерисовки планов с изменением их масштаба, именно для уменьшения планов, пользуются пантографами.

Производство геодезических инструментов — отрасль промышленности для нашего отечества еще новая, но у наших соседей за границей насчитывается немало фабрик, переживших в своей деятельности столетие, и там эта отрасль точного механического дела достигла высокой степени совершенства. В особенности в Германии повсюду рассеяны большие и малые мастерские, из которых иные имеют всемирную известность. Из современных русских фабрик геодезических инструментов следует отметить: в Петербурге — механическую мастерскую военно-топографического отдела главного штаба, в Варшаве — Г. Герлях, в Москве — Швабе, Таубер, Цветков и К^о, Трындина и Громова.

И. Иверонов.