Гироскоп

Гироскоп, тело вращения со свободной осью. Ось быстро вращающегося гироскопа может свободно перемещаться в пространстве, оставаясь параллельной самой себе; если же ее пытаться поворачивать, то при этом гироскоп выказывает устойчивость и сопротивляется этому поворачиванию. Устойчивость гироскопа будет тем больше, чем больше угловая скорость его вращения, чем больше его момент инерции относительно оси вращения, и чем больше скорость, с которой желают повернуть гироскоп. Общеизвестным гироскопом является обыкновенный волчок. Как известно, волчок, находящийся в покое, нельзя поставить на конец его оси — волчок сейчас же падает; но если волчку сообщить вращение, то он стоит, не падая, причем ось его совершает конусообразные движения в пространстве. Перемещения оси тем медленнее, чем быстрее вращается волчок: по мере того как скорость вращения волчка уменьшается — увеличиваются число и величина размахов его оси, пока он окончательно не упадет.

Свойством гироскопа Фуко — становиться в плоскости меридиана — пользуются в настоящее время для замены магнитного компаса компасом гироскопа. В этих приборах диск гироскопа приводится в движение электричеством. Преимущество компаса гироскопа в том, что он дает всегда вполне точные показания, не завися от влияний металлических масс, окружающих компас.

Теми же свойствами гироскопа объясняется устойчивость оси вращающегося снаряда, вылетевшего из нарезного орудия.

Шликом предложено пользоваться гироскопом для уменьшения качки судов, для чего гироскоп громадных размеров устанавливается на судне и сообщает последнему большую устойчивость. Произведенные опыты дали очень благоприятные результаты. Точно также вагоны Бреннан-Шерловского типа, двигающиеся по одному рельсу, сохраняют свою устойчивость благодаря поставленным внутри вагона гироскопам.

См. приложение: Гироскоп.

Гироскоп

Пусть (фиг. 1) плоскость А вращается равномерно с угловой скоростью ω около оси ZZ' и в этой плоскости движется некоторая материальная точка М под действием силы Р, лежащей в плоскости А. Для того, чтобы плоскость могла вращаться равномерно, мы должны приложить к точке М силу N', равную и противоположную нормальному давлению N, производимому на плоскость А движущейся по ней материальной точкою М. Предположим, что такая сила N' действительно приложена, и постараемся определить ее величину.

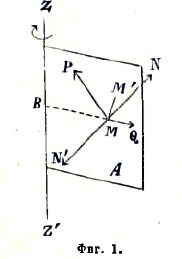
Относительное движение точки М в плоскости А совершается так, как будто бы эта материальная точка кроме силы Р была подвержена еще центробежной силе Q,’ которая, как известно, направлена по продолжению перпендикуляра ВМ, опущенного из М на ось ZZ', и выражается формулой

Q = mω²y,

где m есть масса материальной точки, а y=BM. Предположим, что в бесконечно малое время τ материальная точка проходит элементарный путь ММ' = σ, направление которого образует с осью ZZ' угол α, и напишем теорему живых сил для относительного движения ее:

раб. P+mω²yσsinα = mv’²/2 – mv²/2,

где v и v’ суть скорости относительного движения в М и М'.

Кроме этого напишем теорему живых сил для абсолютного движения нашей материальной точки, которое совершается только под действием сил Р и N':

раб.  P+N’ωyτ = m/2{v’²+ω²(y+σsinα)} – (m/2)(v²+ω²y²)

Вычитая из этого равенства предыдущее, разделяя на ωyτ и отбрасывая бесконечно малый член, получаем:

N’ – mω²(σ/τ)sinα = mω²(σ/τ)sinα

откуда следует, что

N=2mωvsinα  (1)

Если бы мы предположили, что материальная точка движется от М' к М, то нашли бы во второй части формулы (1) знак (—). Это показывает, что сила давления движущейся материальной точки на плоскость А совершается в сторону противоположную вращению этой плоскости, когда материальная точка удаляется от оси ZZ', и в сторону вращения плоскости А, если материальная точка приближается к оси ZZ'.

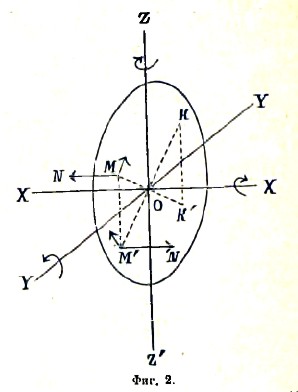
Вообразим (фиг. 2), что в плоскости YOZ лежит бесконечно тонкий материальный диск, вращающийся с весьма большой угловой скоростью 2 около оси XX', проходящей чрез центр диска О и перпендикулярной его плоскости, и допустим, что эта ось в свою очередь приведена во вращательное движение около перпендикулярной ей оси ZZ' с угловой скоростью ω. Каждая частица диска будет при этом давить на плоскость YOZ силой N, определяемой по формуле (1). Проведем из точки О ось YY', перпендикулярную к осям XX' и ZZ', и возьмем относительно ее две симметричные частицы диска М и М'. Называя через r расстояния этих частиц от центра 0 и через α — угол MOY, найдем по формуле (1) для силы оказываемого ими давлении величину

N=2mωΩrSinα.

При этом давление частицы М будет направлено в сторону вращения ω, а давление частицы М' — в обратную сторону. Эти две силы давления образуют пару (N₁—N), момент которой будет такой:

2mωΩrSinα.MM’ = 4mωΩr²Sin²α

Пара эта стремится повернуть диск около оси YY' так, чтобы ось вращения 2 приблизилась к оси вращения ω (оси мы считаем направленными в ту сторону, глядя из которой вращение совершается по солнцу). Такие же пары будут получаться для симметричных точек, взятых на площади диска за осью ZZ'. Если сложим найденную пару сил с парой сил давлений, происходящих от влияния симметричных точек К и К', радиусы ОК и ОК' которых тоже равны r, а по направлению перпендикулярны радиусам ОМ и ОМ', то найдем равнодействующую пару с моментом

4mωΩr²Sin²α + 4mωΩr²Cos²α = 4mωΩr²

Отсюда следует, что момент L равнодействующей пары, происходящей от давления всех частиц диска на плоскость YOZ, будет

L = 4ωΩΣmr²

где сумма распространяется на четверть диска, или

L =  ωΩΣmr²,  (2)

где сумма распространяется на весь диск.

Если бы мы имели не бесконечно тонкий диск, а какое-нибудь тело вращения относительно оси XX', то мы могли бы его разбить на бесконечно тонкие диски и, определив пару, соответствующую каждому из них, по формуле (2), сложить моменты всех этих пар (причем то обстоятельство, что ось ZZ', около которой совершается вращение ω, не будет лежать в плоскостях дисков, не окажет влияния на определение давлений N). Вследствие этого замечания формула (2) приложима к какому-нибудь телу вращения, причем входящую в нее сумму надо распространять на все частицы тела. Такая сумма называется моментом инерции тела относительно оси XX'.

Наконец, если бы ось вращения ω образовывала с осью вращения Ω некоторый угол β, то следовало бы разложить вращение ω на вращение, совершающееся около оси, перпендикулярной Ω, и на вращение, совершающееся около этой оси. При этом рассматриваемая нами пара будет зависеть только от первого вращения, и так как угловая скорость этого вращения есть ωSinβ, то момент пары будет:

L = ωSinβΩΣmr² (3)

Из всего сказанного получается наша основная теорема. Если какое-нибудь тело вращения вращается около своей оси с угловой скоростью Ω и мы будем повертывать ось этого тела около некоторой оси, образующей с осью тела угол β, с угловой скоростью ω, то явится пара с  моментом, равным произведению ωΩSinβ на момент инерции тела, стремящаяся повернуть ось тела к  оси сообщаемого вращения так, чтобы при совпадении осей вращения Ω и ω совершались бы в одну сторону.

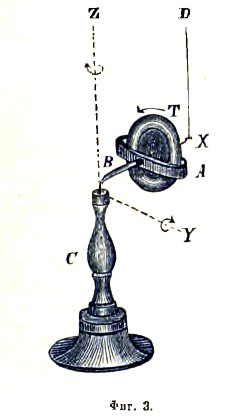
Гироскопы Фуко (Foucault) и Плюкера (Plucker). Фуко устроил два гироскопа, из которых первый представлен на (фиг. 3). Он состоит из тора Т, ось которого укреплена в кольце А; эго кольцо соединено с рычагом В, опирающимся с помощью острия О па подставку С. Тор приводится с  помощью особого механизма (системы зубчатых колес) в быстрое вращение Ω, которое мы будем воображать совершающимся по солнцу для наблюдателя, глядящего от Х к О. Потом рычаг опирают концом О на подставку и держат горизонтально с помощью нити XD; при этом натяжение нити будет таково, как если бы тор не вращался, потому что указанная нами пара L может явиться только при поворачивании оси тора. Если нить пережечь, то тор начинает падать, и ось его вращается около оси OY по солнцу. Вследствие этого является пара, которая, стремясь повернуть ось тора ОХ к оси OY, сообщит гироскопу вращение около оси OZ тоже по солнцу; от этого вращения в свою очередь явится новая пара, которая, стремясь повернуть ось ОХ к оси OZ, будет уничтожать скорость падения гироскопа и уравновешивать его вес. После нескольких колебаний (которые затухнут от трения точки опоры и сопротивления воздуха) гироскоп начнет вращаться около оси OZ с постоянной угловой скоростью ω, удерживаясь на весу действием пары L, определяемой по формуле (3). При этом вращение ω будет тем менее, чем более скорость Ω, что прямо видно из формулы. Когда, по прошествии некоторого времени, Ω начнет уменьшаться, то гироскоп начнет вращаться около оси ОZ все скорее и скорее. Если перед рычагом ВО поставить какое-нибудь неподвижное тело, например, держать карандаш, то, как только рычаг подойдет к карандашу, гироскоп сейчас же опустится вниз. Это происходит оттого, что при ω=0 имеем в формуле (3) L=0. Если хотим пустить гироскоп, удерживая его сначала рукой за точку Х, то следует сразу отнимать руку, потому что при робком отнятии можно уронить гироскоп.

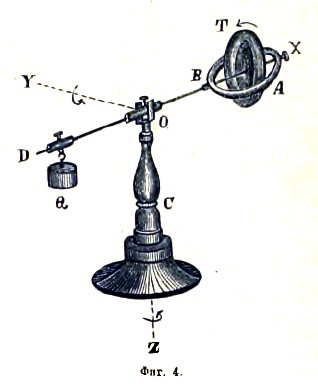
Гироскоп Плюкера, представленный на (фиг. 4), отличается от вышеописанного присоединением противовеса Q. Здесь рычаг BD, держащий кольцо А, проходит в точке О через муфту (которая может вращаться около горизонтальной и вертикальной оси) и несет на своем продолжении OD подвижный груз Q.

Поместив груз так, чтобы он перевешивал гироскоп, приведем тор с помощью нитки в быстрое вращение 2 по солнцу, для наблюдателя, глядящего от Х к О; потом, удерживая гироскоп рукой за точку Х, поставим рычаг горизонтально и быстро отнимем руку. Вследствие падения груза Q тор Т будет подниматься и вращаться около оси OY по солнцу. Это образует пару, которая, стремясь приблизить ось ОХ к оси OY, сообщит гироскопу вращение ω около вертикальной оси для наблюдателя, глядящего сверху, против солнца, а для наблюдателя, глядящего снизу от Z в О, по солнцу. От этого последнего вращения явится пара L, стремящаяся приблизить ось ОХ к оси OZ, которая будет уравновешивать груз Q. Это равновесие установится после нескольких колебаний, и гироскоп, держась на весу, будет равномерно вращаться около вертикальной оси против солнца для наблюдателя, глядящего сверху. Разумеется, что, передвинув или сняв гирьку, мы можем гироскоп Плюкера заставить двигаться так же, как гироскоп Фуко.

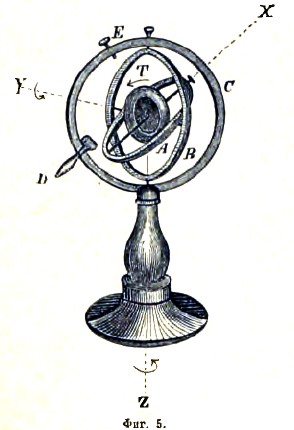
Гироскоп Броненберга (Bohnenberger). Броненберг  устроил гироскоп (фиг. 5), в котором тор Т имеет так называемый кардановский подвес, позволяющий ему свободно вращаться около всякой оси, проходящей через центр тора О. Приведем кольцо В в плоскость неподвижного кольца С и скрепим их штифтом Е; сообщим тору с помощью нитки быстрое вращение и толкнем кольцо А. Мы увидим, что это кольцо будет вращаться вместе с осью тора, как будто бы тор не имел вращения около своей оси. Это произойдет оттого, что вследствие штифта Е кольцо В не может вращаться от действующей на него пары, а если нет вращения кольца В, то нет и пары, стремящейся вращать тор около оси OY кольца А. Совсем другое явление представляется, когда мы вынимаем штифт Е. Тогда удар в кольцо А почти не приводит его в движение, и чем мы сильнее ударяем, тем более нам сопротивляется кольцо А, так что, пользуясь для удара небольшим деревянным молотком D, мы чувствуем, как будто ударяем по неподвижному телу. Это объясняется так: сообщая ударом угловую скорость кольцу А около оси ОY, мы развиваем пару сил, которая вращает гироскоп около оси OZ; от этого же вращения в свою очередь развивается пара, стремящаяся подвинуть ось ОХ к оси OZ и уничтожающая вращение кольца А, сообщаемое ударом молотка. В подтверждение сказанного, мы будем при всяком ударе молотка замечать поворот кольца В на некоторый угол около оси OZ.

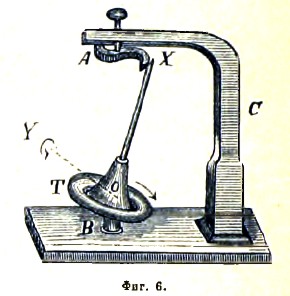
Гироскоп Сира (Sire). Этот гироскоп состоит (фиг. 6) из тора Т, ось которого своим нижним концом опирается острием па подставку В, а своим верхним концом может быть или укреплена в центре горизонтальной фигурки А (тогда ось будет стоять вертикально), или приложена к периметру этой фигурки. Центр тяжести тора лежит на его оси несколько ниже нижней точки опоры. Сначала, приподняв фигурку А с помощью верхней пуговки, укрепляют верхний конец оси в центре фигурки и приводят тор Т с помощью нитки в быстрое вращение. Потом, несколько подняв фигурку А, толкают ось тора в сторону так, что она начнет описывать некоторый конус (явление, объясненное на ст. 4). Далее несколько опускают фигурку А и стараются прикоснуться ее периметром к оси тора. Как только это случатся, то ось тора как бы прилипнет к периметру фигурки и будет катиться по нем, следуя за всеми его изгибами. Это явление объясняется так: когда мы прикоснемся краем фигурки А к оси тора, то, вследствие небольшого давления между фигуркой и осью, последняя покатится по периметру фигурки, вследствие чего образуется вращение около оси ОY, а это обстоятельство послужит  образованию пары сил, которая, стремясь повернуть ось ОХ к оси OY, будет нажимать ось тора на периметр фигурки А с довольно значительной силой, и эта ось, катясь по периметру, будет следовать за всеми его изгибами.

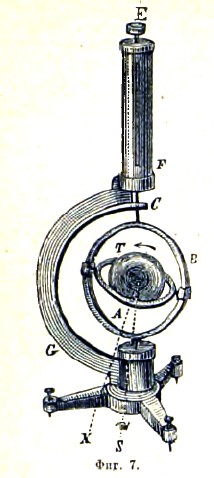
Второй гироскоп Фуко. Второй гироскоп был устроен Фуко для обнаружения вращательного движения Земли. По конструкции он схож с гироскопом Бопенбергера и отличается от него только приспособлениями для уменьшения трения. Эти приспособления (фиг. 7) заключаются в том, что концы оси кольца А заменены стальными призмами, опирающимися на агатовые пластинки в кольце В (наподобие точки опоры весов); кольцо же В верхним острием своей оси проходит чрез направляющую С и подвешивается на нити СЕ, заключенной в футляре F, а нижним острием D проходит чрез отверстие в подставке О. Прибор снабжен установочными винтами, с помощью которых ось его устанавливается в вертикальном положении, и хорошо центрирован, так что тор остается в равновесии во всяком положении. Кроме того мы можем сделать неподвижным кольцо В, опуская с помощью винта Е нить ЕС и опирая нижнее острие D в отверстие подставки, или связать в одно целое кольца А и В (с помощью особого приспособления), причем плоскости их будут взаимно перпендикулярны. Описываемый гироскоп позволит делать три рода наблюдений. Если, сохраняя свободу обоих колец, сообщить тору с помощью системы зубчатых колес быстрое вращение (до 250 оборотов в 1”), то ось тора ОХ будет сохранять свое положение в пространстве, и мы можем по прошествии некоторого времени наблюдать ее относительное перемещение вследствие вращения Земли. Для второго наблюдения мы опускаем нить и устанавливаем кольцо В в плоскости меридиана. Тогда замечаем, что ось тора начнет двигаться и после нескольких колебаний около положения, параллельного оси Земли, установится в этом положении так, что наблюдатель, глядящий сверху (в северном полушарии), будет видеть вращение тора против солнца. Это объясняется так: все движения подставки гироскопа, происходящие от движения Земли, может быть разложено на некоторое поступательное движение и на вращение по солнцу около оси OS, параллельной оси Земли, причем S направлено на юг; от этого вращения является пара, сил, стремящаяся ось тора ОХ соединить с осью OS, и так как этому движению сопротивляется только весьма малая сила трения призм, то после нескольких колебаний ось ОХ займет положение OS. Чтобы произвести третье наблюдение, скрепляем между собой кольца А и В и поднимаем нить, причем кольцо А становится горизонтально; тогда замечаем, что кольцо В по прошествии некоторого времени становится перпендикулярно к плоскости меридиана. Это объясняется так: вертикальная плоскость, проходящая чрез прямую OS, и есть плоскость меридиана; если ось тора ОХ не лежат в этой плоскости, то, стремясь приблизиться к OS, она будет двигаться в своей горизонтальной плоскости и после нескольких колебаний остановится в плоскости меридиана.

И. Жуковский.