Химия. Химическое равновесие

IV. Химическое равновесие. В механике мы принимаем, что система находится в равновесии, если силы, действующие на нее, взаимно уничтожаются. В химии понятие о равновесии есть понятие термодинамическое и значительно сложнее, чем в механике. В термодинамике мы пользуемся обобщенным понятием о силах; говорить о взаимном уравновешивании (нейтрализации) таких сил нельзя. В системе, находящейся в равновесии с точки зрения термодинамики, покоя нет; в такой системе непрерывно текут минимум два процесса во взаимно противоположных направлениях, причем взаимно уничтожаются не силы, а результаты двух процессов. Так, в замкнутой системе, содержащей жидкую воду и ее пар в состоянии равновесия при постоянных внешних условиях, протекают два процесса: парообразования и конденсации, причем во всякий момент столько же образуется пара, сколько его и конденсируется.

Рассматриваемые в химии системы (обособленные части пространства, содержащие материю и энергию) обладают физико-химическими свойствами; из их числа мы выделяем в особую группу термодинамические свойства; к последним относятся: объем, давление, температура, энергия, энтропия, концентрации веществ и все те свойства, которые являются функциями перечисленных основных свойств и только их. Опыт показал, что для определения состояния системы достаточно выбрать некоторое число свойств (начиная от двух) в качестве независимых величин (переменных), все остальные свойства будут их функциями. Обычно в качестве независимых переменных выбирают: температуру, объем (или давление) и концентрации веществ в системе. Мы говорим, что система находится в равновесии, если переменные, определяющие ее состояние, во времени не изменяются, другими словами, стационарное состояние мы принимаем за равновесие.

В основе учения о равновесии физико-химических систем лежит постулат Гиббса (см.), главнейшая форма которого гласит: «для того, чтобы замкнутая система находилась в равновесии, необходимо, чтобы изменения ее внутренней энергии при данном объеме и данной энтропии не превышали бесконечно малых величин 2-го порядка». Замкнутость системы характеризуется постоянством ее массы. Бесконечно малые изменения энергии первого порядка должны равняться нулю, второго же порядка могут быть больше, меньше или равны нулю, соответственно чему равновесие будет устойчивым, неустойчивым или безразличным. Другими словами, замкнутая система находится в устойчивом равновесии, если ее внутренняя энергия при данном объеме и данной энтропии имеет минимальное из возможных значений. Вместо полной внутренней энергии можно оперировать с той ее частью, которая носит название свободной энергии, причем условием устойчивого равновесия будет минимальное ее значение при данном объеме и данной температуре.

Мы различаем два класса систем. К первому классу принадлежат системы, в которых протекают физические процессы, в том числе изменения агрегатного состояния, но в которых химическая природа веществ ни качественно, ни количественно не претерпевает изменений; такие системы представляют собой или индивидуальные вещества или их смеси. Они могут быть в устойчивом, неустойчивом или безразличном состоянии равновесия. С опытной точки зрения неустойчивое равновесие бывает метастабильным (реализуемым, — например, состояние перегретой воды или переохлажденного пара) или лабильным (нереализуемым, ср. уравнение состояния ван дер Ваальса, XII, 313).

В системах второго класса наряду с физическими процессами протекают химические обратимые реакции, причем всякому бесконечно малому изменению внешних условий отвечает бесконечно малое изменение концентраций веществ, входящих в систему. Изменения концентраций управляются законами смещения равновесия и в частности законом действующих масс, открытым сначала Гульдбергом и Вааге эмпирически, потом выведенным, как следствие, из постулата Гиббса.

В системе протекает реакция n₁A₁ + n₂A₂ + … ↔ m₁B₁ + m₂B₂ +…;  пусть концентрации веществ

при равновесии равны  A₁,  A₂, …, B₁, B₂, … при равновесии равны С_A1,  С_A2, …, С_B1, С_B2, …  закон действия масс, правильнее, закон концентраций гласит, что при постоянной температуре и давлении

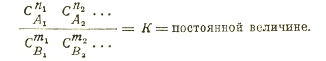
Системы первого класса могут или оставаться системами того же класса при всех доступных нам температурах и давлениях, как, например, инертные газы и их смеси, или же такие системы при высших температурах переходят в системы второго класса. Так, система из аргона и углекислоты при температурах ниже 1000° — 1 класса, при высших — второго, так как при температурах выше 1000° начинается диссоциация углекислоты и в системе происходит обратимая химическая реакция СО₂ ↔ СО + ½ О₂. Смесь водорода и кислорода — при невысоких температурах система первого класса, при высоких — второго класса (образование и диссоциация воды H₂O ↔ H₂ + ½ О₂. Однако, здесь мы встречаем нечто новое; система первого класса: водород +  кислород, оставаясь замкнутой, может быть переведена необратимым способом при помощи катализатора при средних и низких температурах в систему тоже первого класса, но отличного химического состава, а именно в систему из воды и избытка того или другого газа. Последняя система обладает меньшей свободной энергией, нежели первая. Термодинамика не может предвидеть существование в равновесных состояниях таких систем, как смесь водорода и кислорода в обычных условиях. Другими словами, всякий раз, когда термодинамика утверждает, что система в данных условиях будет в состоянии равновесия, это действительно имеет место; но могут быть случаи, что система будет в равновесии и при условиях, при которых, с точки зрения термодинамики, она не должна была бы быть в равновесии. Дюгем такие равновесия называл ложными; ряд ученых отрицает состояние равновесия в таких случаях и заявляет, что в них идут процессы, но с весьма медленной скоростью, недоступной измерению (Оствальд; «дрова горят не только в печке, но и перед печкой»). Урбен и др. ученые считают такие объяснения нелогичными; с точки зрения опытной система из водорода и кислорода ведет себя как система первого класса и должна рассматриваться как таковая. Такие системы с физической точки зрения могут быть в устойчивом, неустойчивом или безразличном равновесии, но каждое такое состояние неустойчиво с химической точки зрения. Критерий наиболее химически устойчивого (абсолютного) равновесия отсутствие катализатора, который мог бы перевести данную систему в еще более устойчивую систему.

В общем случае система может состоять из нескольких составных веществ и распадаться на части — фазы, отделенные друг от друга видимыми поверхностями раздела. Система, содержащая воду и соль, может состоять из четырех (или меньше) фаз: парообразной, жидкой (раствора), льда и твердой соли. Фазой называется комплекс образований, обладающих одинаковым составом и одинаковыми термодинамическими свойствами; следовательно, отдельные льдинки или кристаллики соли образуют одну фазу. Составными веществами системы называются те вещества, которые могут существовать в изолированном состоянии; следовательно, отдельные ионы соли не считаются составными веществами системы. Из числа составных веществ мы выбираем наименьшее число их, достаточное для того, чтобы с их помощью выразить состав любой фазы системы, находящейся в равновесии, и называем их компонентами (или независимыми составными веществами). В системах первого класса число составных веществ совпадает с числом компонентов, в системах второго класса компонентов меньше, нежели составных веществ, на число обратимых реакций, протекающих в системе в данных пределах температур и давлений.

Примеры. Система состоит из углекислого кальция (мела), окиси кальция (извести) и углекислоты, всего три составных вещества; в системе идет реакция СаСО₃ ↔ СаО + СО₂; независимых составных веществ (компонентов) 3—1 = 2. Система состоит из Н₂О, KCl, NaCl, Na₂SO₄, K₂SO₄, NaCl 2Н₂O и Na₃SO₄ 10Н₂O, всего 7 составных веществ; в системе идут реакции: 1) 2KСl + Na₂SO₄ ↔ K₂SO₄ + 2NaCl, 2) NaCl 2Н₂O ↔ NaCl + 2Н₂O и 3) Na₂SO₄ 10Н₂О ↔ Na₂SO₄ + 10Н₂O; компонентов 7—3=4.

Из постулата Гиббса о равновесии вытекают следующие условия устойчивого равновесия в случае многофазных (гетерогенных) систем, находящихся под влиянием одной только силы, давления: 1) температура и давление во всех фазах должны быть одинаковыми; 2) одинаковые значения во всех фазах должны иметь так называемые термодинамические (или химические) потенциалы¹⁾ каждого из компонентов; 3) число фаз в равновесной системе определяется законом Гиббса k ≤ n +2 (правило фаз: число фаз k равно или меньше числа n компонентов плюс два).

¹⁾ Внутренняя энергия системы состоит из различных частей (слагаемых); увеличение массы ∂m компонента влечет за собою увеличение ∂u энергии системы на величину, равную произведению из прироста массы компонента dm на термодинамический (химический) потенциал его μ = ∂u/∂m при прочих постоянных условиях. Химический потенциал вещества аналогичен температуре или электрическому потенциалу, но, к сожалению, для его измерения не существует таких методов и приборов, как для измерения температуры или электрического потенциала.

В однокомпонентных системах (n=1) максимальное число фаз, могущих находиться в равновесии, — три. Например, система, состоящая из воды, может состоять одновременно максимум из трех фаз: пара, жидкой воды и льда. В двухкомпонентных системах (n = 2) максимум фаз равен 4; например, в системе: вода соль, возможно равновесие четырех фаз: пара, раствора, соли и льда. Разность f =  n + 2 — k называют степенью свободы системы. Однокомпонентные системы при трех фазах, двухкомпонентные — при 4 фазах и т. д. не имеют ни одной степени свободы, т. е. они могут существовать только при строго определенных условиях давления, температуры и (для систем дву- и более компонентных) концентраций составных веществ. Так, пар, жидкая вода и лед (однокомпонентная система) могут существовать в равновесии при + 0,0076° и 4,579 мм  давления. Всякое изменение температуры или давления влечет за собою процесс, в результате которого одна из фаз исчезает. Такое состояние системы называется инвариантным. Если на оси абсцисс (рис. 1) будем откладывать температуры, на оси ординат давления, то инвариантное состояние однокомпонентной системы выразится точкой О на плоскости. В случае двухкомпонентных систем прибавится третья ось — ось концентраций, и инвариантное состояние такой системы выразится точкой в пространстве. Очевидно, что в случае 3 компонентов необходимы две оси для концентраций, и инвариантное состояние трех компонентных систем выражается точкой в четырехмерном пространстве. На практике прибегают к упрощенным обходным способам графического изображения многокомпонентных систем. Если число фаз в однокомпонентной системе 2 (двухкомпонентной — 3, и т. д.), то f = n + 2 — k = 1, система имеет одну степень свободы (моновариантная система, правильнее, система находится в моновариантном состоянии). В этом  случае одно из внешних условий (температуру, давление или концентрацию) мы можем в определенных конечных пределах изменять без того, чтобы число фаз изменилось. Так, в случае воды, система, состоящая из жидкой воды и пара, может существовать при разных температурах. Графически (рис. 1) моновариантное состояние системы выражается кривой линией, показывающей, как изменяется давление системы с температурой. Из трех фаз можно составить три комбинации по две, каждая комбинация на рис. 1 дает отдельную кривую равновесия (ОА — кривая равновесия пара и жидкости, ОВ — льда и пара, ОС — жидкой воды и льда). Все кривые исходят из точки О инвариантной системы, называемой тройной точкой. В случае двухкомпонентной системы получим 4 кривые (в пространстве) равновесия трех фаз, исходящие из точки инвариантной системы, называемой в этом случае четверной точкой, и т. д.

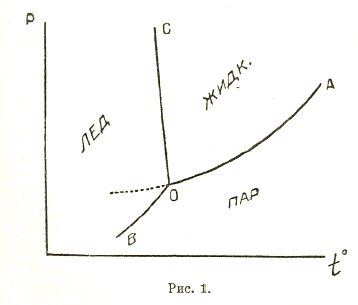
Все системы в моновариантном состоянии обладают замечательным свойством: в них давление не зависит от объема; так, в случае воды и пара, изменение объема не изменяет давления пара, а изменяет только относительные количества фаз.

При наличии в однокомпонентной системе одной только фазы, в двухкомпонентной — 2 фаз и т. д., система обладает двумя степенями свободы, т. е. в таких системах мы можем менять две переменные (например, давление и температуру или давление и одну из  концентраций) без того, чтобы число фаз изменялось. На рис. 1 таким бивариантным системам отвечают части плоскости между двумя кривыми; в случае двухкомпонентной системы — поверхности между кривыми, и т. д. Чем больше система содержит компонентов, тем больше может быть ее вариантность; системы, степень свободы которых больше 2, часто называются поливариантными.

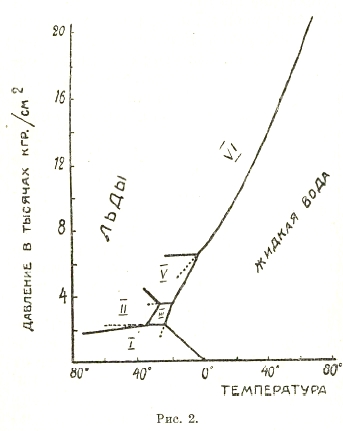
Следует отметить, что термодинамика дает точный ответ о характере данного равновесия системы; например, она определенно говорит, что однокомпонентная система может образовать инвариантную систему при наличии трех фаз и три моновариантных при наличии двух фаз, т. е. может дать тройную точку с 3 кривыми, исходящими из нее; но термодинамика не может сказать, сколько тройных точек может образовать такая система, это дело опыта, а опыт говорит, что тройных, четверных и т. д. точек у систем с данными компонентами может быть много. Так, в случае воды, может быть несколько родов льда, устойчивых при разных температурах и давлениях; одновременно в равновесии могут быть только три фазы, но при наличии разных льдов возможны различные комбинации по три фазы (различные тройные точки). Рис. 2 показывает диаграмму равновесия в системе из воды в различных состояниях. Здесь тройные точки: 1) O, см. рис. 1 (пар, вода, лед I — обыкновенный), 2) С — вода, льды I и III, -22° и 2115 кг/см² давления, 3) D — вода и льды III и V, — 17° и 3530 кг/см², 4) F — льды I, II, III, -34,7°, 2170 кг/см², 5) S — льды II, III, V, —24,3° и 3510 кг/см², 6) Е — вода, льды V и VI, + 0,16° и 6380 кг/см². Последняя кривая (моновариантная система: вода и лед VI) прослежена до + 80° и 20 000 кг/см² давления («горячий» лед). Различные льды являются полиморфными разностями, модификациями, представляющими каждая самостоятельную фазу. Так как каждое вещество может существовать в различных модификациях (теорией неучитываемых), то однокомпонентная система может иметь ряд тройных точек. В двухкомпонентных (и выше) системах четверные, пятерные и т. д. точки также возможны во множественном числе не только в силу существования полиморфных разностей веществ, но и в силу существования химических соединений, тоже теорией не учитываемых; так, в системе сернокислый натрий + вода имеется ряд инвариантных состояний в виду существования двух полиморфных разностей сернокислого натрия (ромбического и моноклинического) и кристаллогидратов Na₂SО₄ 10Н₂О и Na₂ SO₄ 7Н₂О, т. е., считая раствор и пар, возможны 6 фаз, существовать же одновременно могут только 4, следовательно, возможны разные четверные точки.

Правило фаз, частное, но весьма обширное следствие постулата Гиббса в равновесии, является классификационным началом в грандиозной области химического равновесия. Без него невозможно было бы современное развитие не только физической химии, но и неорганической и ряда глав химической технологии (ср., например, сплавы металлов, учение о силикатах в технике).

А. Раковский.