Исчисление (Исчисление бесконечно малых)

Исчисление бесконечно малых

Исчисление бесконечно малых, или высший анализ, представляет отдел математики, в основании которого лежит особый метод — метод бесконечно малых и тесно связанный с ним метод пределов. Метод бесконечно-малых применяется главным образом к изучению непрерывно изменяющихся величин, а затем и во всех тех случаях, когда искомая величина не может быть получена при помощи конечного ряда действий, но мы можем подойти к ней как угодно близко. Главные отделы исчисления бесконечно малых — исчисления дифференциальное и интегральное.

I. Бесконечно малые величины. Потребность в особом методе для решения указанных выше задач сознавалась уже давно. В  греческой геометрии (Евдокс, Евклид, Архимед) для этой цели применялся метод исчерпывания, сущность которого будет ясна из следующего примера. Чтобы доказать, что площадь круга равна площади треугольника, у которого основание равно окружности этого круга, а высота — радиусу, Архимед вписывает в круг ряд правильных многоугольников, из которых каждый следующий имеет вдвое более сторон, чем предыдущий; тогда каждый новый многоугольник получается из предыдущего через прибавление некоторой площади, Архимед показывает, что площади этих вписанных многоугольников как угодно близко подходят к площади круга — они исчерпывают эту площадь. Если теперь предположить, что доказываемая теорема не верна, и площадь круга меньше площади вышеупомянутого треугольника, то оказалось бы, что площадь круга меньше площади некоторого вписанного в него многоугольника, что невозможно; точно так же, если бы площадь круга была более площади вышеупомянутого треугольника, то она была бы больше площади некоторого описанного многоугольника, что также невозможно. Таким образом, площадь круга не может быть неравна площади упомянутого треугольника, и теорема доказана. Легко видеть, что это доказательство, в сущности, то же самое, каким пользуются и теперь в учебниках геометрии. Вообще, метод исчерпывания сохранился до сих пор в обычном изложении элементарной геометрии. Его главный недостаток в отсутствии общности; доказательство должно существенно видоизменяться для каждого отдельного предложения.  

В XVI—XVII веках, с возникновением точного естествознания в аналитической геометрии, явилась необходимость в математических методах, пригодных для изучения непрерывно-изменяющихся величин. Галилей, Кеплер решали задачи о движении тел, о вычислении объемов тел и длин линии и т. п., Кавальери (1635) в своем методе неделимых (methodus indivisibilium) рассматривает непрерывную величину, как состоящую из неограниченного множества неделимых частей; так, площадь рассматривается, как совокупность неограниченного множества параллельных линий, не делимых на более тонкие. Галилей, Кеплер также смотрели на непрерывную величину, как на составленную из бесконечного множества бесконечно малых частей. Эти взгляды подготовило появление анализа бесконечно малых.

Изобретение исчисления бесконечно малых, как особого метода, принадлежит Ньютону и Лейбницу, пришедших одновременно к основной идее этого исчисления. Лейбниц изложил основания дифференциального исчисления в мемуаре, напечатанном в 1681 г. в лейпцигских «Acta Eruditorum», под заглавием: «Nova methodus pro maximis et minimis itemque tangentibus quae nec fractas nec irrationales quantitates morutur, et singulare pro illis calculi genus». В другом мемуаре, напечатанном там же в 1686 г. — «De geometria recondita et analisi indivisibilium atque infinitorum» - Лейбниц изложил основания интегрального исчисления. Ньютон дал основные идеи своего «метода флюксий» в 1686 г. в знаменитой книге «Philosophiae naturalis principia mathematica», но самые обозначения метода флюксий появились в печати только в 1693 г. в письме Ньютона, напечатанном в собрании сочинений Wallis'а. Однако несомненно, что Лейбниц и Ньютон пришли к новым методам значительно ранее — Лейбниц около 1675 г., Ньютон около 1671 г. Впоследствии между Ньютоном и Лейбницем возник спор о первенстве в изобретении нового исчисления. Этот спор принял очень острый характер, так как сторонники Ньютона обвиняли Лейбница в том, что он заимствовал основную идею метода из необнародованных писем Ньютона. В настоящее время этот спор потерял большую часть своего значения; изобретение исчисления бесконечно малых уже было в то время в значительной степени подготовлено трудами предшествовавших ученых, и хотя Лейбниц не мог из переписки с Ньютоном узнать об некоторых его открытиях, но метод Лейбница настолько отличен от метода Ньютона, что и Ньютон и Лейбниц должны в равной степени считаться основателями исчисления бесконечно малых.

Метод Лейбница, основанный на применении бесконечно малых величин — дифференциалов, быстро распространился среди ученых континентальных стран   Европы, хотя в то же время принцип метода, вызывал и возражения, как недостаточно строгий. К ближайшим по времени ученым, содействовавшим дальнейшему развитию высшего анализа, принадлежат братья Бернулли (см.), Лопиталь, составивший первый систематический трактат по анализу бесконечно малых (1696), Даламбер (1717—1783). Эйлер (1707—1783) объединил исследования по высшему анализу в трех трактатах: «Introductio in Analysin Infinitorum» (1718), «Institutiones Calculi Differentialis» (1755) и «Institutiones Calculi Integralis» (1768—1770).

В Англии метод Ньютона разрабатывали далее Котес (1682—1716) Тэлор (1685—1731), Маклорен (1698—1746). Последний в своем «Treatise on Fluxions» успешно отразил возражения философа Беркли против основных принципов нового метода. Обозначения Ньютона исключительно употреблялись английскими математиками до 1820 г., когда изучению дифференциального исчисления было введено в английские университеты; с этого времени и в английской школе стали также пользоваться, как и на континенте, символами Лейбница.

Дальнейшему развитию и более строгому обоснованию высшего анализа содействовали, далее, Лагранж (1736—1813), стремившийся дать атому отделу математики чисто алгебраическое основание, и Коши (1789—1857), положивший в основание исчисления бесконечно малых метода пределов. Исследования Римана (1826—1866) открывают собой критический период математики, одной из задач которого является точное установление тех условий, при которых справедливы предложения высшего анализа.

К понятию бесконечно малой величины можно прийти следующим путем. Если мы имеем две однородных величины, рассматриваемые абсолютно, т. е. независимо от их знака, например, два промежутка времени или два прямолинейных отрезка, то такие величины обладают тем свойством, что повторив меньшую величину достаточное число раз, мы всегда можем получить величину большую всякой другой с ней однородной. Так, имея сколь угодно малый отрезок и отложив его достаточное число раз, мы можем получить отрезок, больший всякого другого заданного отрезка. Эго свойство, принадлежащее всем величинам, обыкновенно рассматриваемым в математике, носит название аксиомы Архимеда. Для величин, допускающих неограниченное деление на равные части, эта аксиома может быть, очевидно, выражена иначе: каждая величина может быть разделена на такие равные части, что каждая из них будет меньше любой другой величины, с ней однородной; так, каждый данный отрезок можно разделить на равные части, меньшие другого данного отрезка. Аксиоме Архимеда подчиняются и все действительные (вещественные) числа, целые, дробные и иррациональные, кроме нуля. Но рядом с величинами, подчиняющимися аксиоме Архимеда, в математике рассматриваются величины, ей не подчиняющиеся. Если мы имеем две таких величины а и а₁ что сколько бы раз мы ни брали а₁ мы никогда не получим величины, большей, чем а, и обратно, на сколько бы равных частей мы на делили а, мы никогда не получим величины, меньшей, чем а₁ — то величина а₁ называется по отношению к  а бесконечно малой, а величина а по отношению к а₁ — бесконечно большой. Основные величины, рассматриваемые обыкновенно в математике, относительно которых определяется характер бесконечно малых и бесконечно больших величин, как промежутки времени, отрезки, обыкновенные числа, называются величинами конечными. Величины а₁, обладающие высказанным выше свойством, называются также собственно (или актуально) бесконечно малыми, в отличие от несобственно бесконечно малых, о которых будет сказало далее.

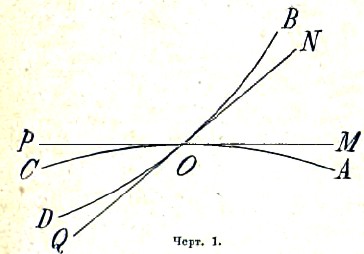
Идею бесконечно малых величин можно пояснить следующим примером. Обыкновенно за угол между двумя пересекающимися линиями на плоскости принимают угол между прямыми, касательными к обеим кривым в точке их пересечения, и в таком случае угол между двумя прикасающимися друг к другу кривыми равен нулю. Но мы можем смотреть на углы иначе и сказать, что величина угла зависит от формы его сторон, причем из двух углов с общей вершиной тот будет считаться меньшим, стороны которого, в непосредственной близости в вершине, заключены между сторонами другого. При таком условии мы будем, например, иметь (черт. 1).

Черт.1

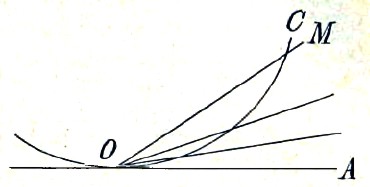
Угол АОВ > угла MON, угол COD < угла РОQ. При таком правиле сравнения углов, угол между кривой и касательной к ней уже не будет нулем, а будет представлять некоторую определенную величину, как это принимал и Евклид (III, 16); это так называемый угол прикосновения. Легко видеть (черт. 2), что если мы проведем через точку прикосновения секущую ОМ, то на сколько бы частей мы ни делили угол АОМ, получаемая часть будет все же более угла АОС; таким образом, угол АОС между кривой и касательной представляет величину бесконечно малую по отношению к каждому углу с прямолинейными сторонами.

Если величина а бесконечно мала относительно а₁ а величина ε бесконечно мала относительно а₁ то ε называется по отношению к а₁ величиной бесконечно малой высшего порядка, нежели а.

Так как бесконечно малая величина менее всякой конечной, то в тех случаях, когда мы ищем только конечные величины, мы можем отбрасывать бесконечно малые слагаемые или вычитаемые, так как при этом мы отбрасываем величины, меньшие, нежели все те, которые подлежат нашему рассмотрению; так, в случае угла между пересекающимися кривыми, например, угол АОВ (черт. 1), мы можем заменить этот угол углом  MON, так как отброшенные углы АОМ и BON бесконечно малы по отношению к углу MON. Но если в данной сумме все конечные слагаемые взаимно уничтожаются, и остаются только бесконечно малые, то ими не всегда можно пренебречь.

Черт. 2

Применение бесконечно малых в анализе основано на том, что действия над бесконечно малыми величинами могут в двух случаях давать в результате величины конечные. С  одной стороны, бесконечно малые величины могут иметь конечное отношение и, следовательно, давать в частном конечное число. С другой стороны, хотя сумма сколь угодно большого числа бесконечно малых слагаемых сама бесконечно мала, но сумма бесконечно большого числа бесконечно малых слагаемых может быть конечной. На первом свойстве основано применение бесконечно малых в дифференциальном исчислении, на втором — их применение в интегральном исчислении.

Вопрос о реальности бесконечно малых величин издавна занимал математиков и философов. Так как прежде всякое изменение мыслилось, как ряд последовательных переходов из одного определенного состояния в другое, то и при рассмотрении непрерывного изменения, например, движение, время и пройденный путь рассматривались, как состоящие из бесконечного множества элементарных неделимых частей, проходимых последовательно. Так смотрели, например, Виет, Галилей, Кавальери, Кеплер и др. Ньютон называл моментами бесконечно малые приращения изменяющихся величин, но не пользовался ими в своей теории, вводя вместо них конечные величины — флюксии.

Лейбниц, по-видимому, признавал реальность актуальных бесконечно малых величин и рассматривал первоначально свои дифференциалы как бесконечно малые приращения переменных величин; но в своем «Nova methodus» он определяет дифференциалы, как некоторые конечные числа, избегая употребления бесконечно малых. Однако, в первом трактате по дифференциальному исчислению, принадлежащем Лопиталю, дифференциалы вновь определяются, как разности двух последовательных значений переменной величины, следовательно, как величины бесконечно малые.

Введение в математику бесконечно малых величин вызвало с разных сторон возражения (Ниепентийт, 1694, Беркли, 1710, и др.). Главное возражение   заключалось в  том, что исследования бесконечно малых не точно, так как  в нем отбрасываются величины, которые хотя и бесконечно малы, но не равны нулю. В другом возражении указывалось на то, что бесконечно малые, как и неделимые, не могут состоять из частей, следовательно, не возможны бесконечно малые  или дифференциалы высших порядков, введение которых было существенно для нового исчисления. С математической  стороны, актуальные бесконечно малые представляют то неудобство, что частное двух таких величин, а также сумма бесконечного множества таких величин не имеют прямого смысла, и потому должны определяться косвенным путем, по способу пределов. Чтобы поставить высший анализ на более прочном основании, метод бесконечно малых был заменен методом пределов, как это предлагали уже Маклорен и Даламбер. Эта замена была выполнена Коши. Тем не менее, метод бесконечно   малых представляет такие удобства, особенно в различных приложениях высшего анализа к другим отделам чистой и прикладной математики, что бесконечно малые, тем не менее, сохранялись в анализе в измененном виде — в виде несобственных бесконечно малых величин, которые правильнее было бы называть, как это делал уже Ньютон, неограниченно малыми. Так как в настоящее время высший анализ имеет дело только с бесконечно малыми величинами этого второго рода, то в последующем мы будем понимать под бесконечно малыми только несобственно бесконечно малые величины. Что касается актуальных бесконечно малых величин, то они встречаются теперь только в общем учении о величинах и в учении о множествах. Бесконечно малые несобственные определяются следующим образом. Пусть мы имеем переменную величину α, которая при своем изменении может сделаться и оставаться меньшей по абсолютной величине каждого данного сколь угодно малого числа ε, |α|< ε; иными словами, пусть это число может при своем изменении сколь угодно близко приближаться к нулю. Такая переменная величина, рассматриваемая в этом ее изменении, и называется несобственно бесконечно малой величиной. Таким образом, тогда как актуально бесконечно малая величина есть величина постоянная или переменная, меньшая всякой конечной величины того же рода, — несобственная бесконечно малая величина есть такая переменная величина, которая при своем изменении может сделаться меньше всякой заданной величины.

С понятием о бесконечно малой величине связано и понятие о пределе. Если переменная х изменяется так, что разность между ней и постоянной а есть величина α бесконечно малая, — т. е., может быть сделана меньше всякой данной величины, то постоянная а называется пределом переменной х при данном ее изменении. Так, площадь круга есть предел площадей вписанных в него правильных многоугольников с увеличением числа их сторон, так как при увеличении числа сторон вписанного многоугольника площадь его неограниченно приближается к площади круга. То что а есть предел переменного х, изображается равенством а=limх, где lim — начальные буквы слова limes — предел. Так как разность х—а между переменным и его пределом равна бесконечно малому α, то х=а+α, т. е., переменное равно своему пределу, сложенному с бесконечно малой величиной. Из предыдущего следует, что бесконечно малое есть переменное, предел которого равен нулю; таким образом исчисление бесконечно малых может быть заменено исчислением пределов.

Если мы имеем несколько бесконечно   малых  α, β, γ, .., зависимых между собой, то одно из них, например α, принимается за главное; тогда, если lim(β/α) равен нулю, β называется бесконечно малым высшего порядка относительно α; если этот предел равен бесконечности, то β называется бесконечно малым низшего порядка; если же этот предел равен конечному числу, то β и α называются бесконечно малыми одинакового порядка. Во многих случаях бесконечно малому β соответствует такое положительное число n, что lim (β/αⁿ) — равно конечному числу; тогда β называется бесконечно малым n-го порядка относительно α. Например, если х стремится к нулю, то, по отношению к х, 2х будет бесконечно малым первого порядка, так как lim(2x/x¹)=2, 3x² – второго, 5√x – половинного; так как из тригонометрии известно, что

lim (sinx/x)
^x=0

т. е. предел sinx/x при x=0, равен единице, то  sin х будет относительно х бесконечно малым первого порядка. Не  нужно думать, что каждому бесконечно малому соответствует определенный порядок малости. Так, в анализе доказывается, что хотя 1/logx бесконечно мало вместе с х, но это бесконечно малое не имеет определенного порядка, так как при всяком n, как бы оно ни было мало, предел отношения (1/logx):xⁿ, при x=0 равен нулю.

II. Дифференциальное исчисление. Основное понятие дифференциального исчисления — понятие производной функции (ср. высшая математика). Производная дайной функции у = f(х) есть предел, к которому стремится отношение между приращением функции у и соответствующим приращением независимого переменного, или аргумента, х, когда последнее стремится к нулю (см. высшая математика). Таким образом, производная от у по х есть не что иное, как предел

lim (Δy/Δx) или
^Δx=0

lim (Δf(x)/Δx) или, что то же
^Δx=0

lim ([f(x+Δx)-f(x)]/Δx)
^Δx=0

Очевидно, что производная не зависит от Δx, так как она получается в пределе, когда Δx неограниченно приближается к нулю; но она, вообще, зависит от х и, следовательно, представляет некоторую функцию от х, определенным образом зависящую от начальной функции f(х). Производная функция обозначается по Лейбницу через dу/dx, по Ньютону у которого производная называется флюксией, через у, по Лагранжу — у’, или f’(х), по Коши df(x)/dx. Если, например, мы имеем y=x², то, чтобы найти производную, составляем разность Δy=(x+Δx)²-x²=2x.Δx+(Δx)², представляющую приращение функции у=х² при переходе от х к x+Δx; затем имеем Δy/Δx=2x+Δx, и, переходя к пределу при Δх = 0, находим производную у' = 2х. Если функция у представляет ординату кривой у = f(х), то производная у' представляет tgα — тангенс угла накопления α между касательной к кривой в точке (х, у) с осью х (ср. высшая математика). Ньютон выводил понятие производной из механики. Обозначим через t время, через s = f(t) расстояние движущейся точки от некоторой начальной точки О. Найдем скорость движения в данный момент времени t. В  этот момент движущаяся точка находится от О на данном расстоянии s. В следующий за моментом t промежуток времени Δt точка пройдет некоторое расстояние Δs. Если бы движение было равномерным, то скорость движения была бы Δs/Δt, т. е. получилась бы делением пройденного пути на время; но, на самом деле, это выражение дает только среднюю скорость за промежуток времени Δt. Чем меньше будет Δt, тем ближе будет эта средняя скорость к истинной скорости движения в момент t. Таким образом, истинная скорость есть предел, к которому стремится отношение Δs/Δt, когда Δt стремится к нулю; и, следовательно истинная скорость в момент t равна

lim Δs/Δt
^Δt=0

 т. е., равна производной от пройденного пространства s по времени t. По Ньютону это есть то значение отношения Δs/Δt, с которым величины Δs и Δt исчезают или возникают; поэтому Ньютон назвал свой метод методом первых и последних отношений. В связи с этим механическим толкованием производной, Ньютон рассматривал непрерывное изменение величин, как течение, и называл функцию флюэнтой, а ее производную, представляющую скорость изменения, флюксией.

В обозначении производной по Лейбницу у'= dy/dx числитель и знаменатель суть два произвольных числа, отношение которых равно производной у'; эти числа называются соответственно дифференциалами переменных у и х. С точки зрения актуальных бесконечно малых, dx и dy суть бесконечно   малые величины, в которые обращаются приращения Δх и Δу при своем неограниченном уменьшении; это — актуально бесконечно малые приращения х и у. Так смотрит на них, например, Лопиталь. Но, с устранением из высшего анализа актуально бесконечно малых, под dx и dy понимают, следуя Лейбницу и Коши, произвольные числа, имеющие отношение у'. Принимая dx равным Δх, получим dy = у'. Δх (см. высшая математика). Хотя, таким образом dx есть вполне произвольное число, но в приложениях анализа к геометрии, механике и естествознанию удобнее понимать под дифференциалами весьма малые числа.

Из определения производной, как предела отношения между приращением функции и приращением аргумента, следует, что производная есть мера быстроты роста функции сравнительно с ростом аргумента: чем больше производная, тем быстрее растет функция сравнительно с аргументом. Так как у' = lim Δy/Δx, то Δy/Δx = у' + ε, где ε стремится к нулю вместе с Δх. Поэтому, если у' положительно, то при Δх, достаточно малом, Δу и Δх имеют знаки одинаковые, а если у' отрицательно, то — разные. Это показывает, что с возрастанием аргумента функция возрастает, если ее производная положительна, и убывает, если производная отрицательна.

Прежде чем перейти к изложению правил дифференцирования функций, т. е. вычисления их производных и дифференциалов, мы приведем здесь некоторые нужные нам свойства функции тригонометрических, показательных и им обратных. Обыкновенно углы выражаются в градусах в их частях; но в анализе удобнее выражать углы в т. н. абсолютной мере, т. е., рассматривая каждый угол, как центральный, измерять его отношением дуги, на которую он опирается, к радиусу соответствующего круга, или, что то же, измерять угол соответствующею ему дугой в круге радиуса, равного единице. При таком измерении углов каждому числу х будет соответствовать свой угол; например, прямой угол будет измеряться не числом 90°, а отвлеченным числом 2π:4, или — π/2 , т. е. 1,57079...; таким образом, мы можем, например, паписать sin π/6 = ½, так как число π/6 соответствует 1/12  полной окружности, т. е. 30°. Что касается показательной функции а^х и логарифмической log_ax, то из них в анализе всего проще те, для которых основанием а служит т. н. Неперово число е, представляющее

lim (1+1/n)^n
n=∞

число е равно 2,718281828459... Логарифмы, вычисленные при этом основании, называются натуральными; мы будем их обозначать через logx.

Основные правила дифференцирования заключаются в следующих соотношениях, данных Лейбницем, которые легко вывести из определения производной. Обозначая через с постоянное, через u, v, w… функции от х, находим, что из u=v следует du=dv. Далее, имеем dc = 0, d(cu) - с.du, d(u±v) = du±dv, d(uv) = v.du + udv, d(u/v) = (vdu-udv)/v²

Деля обе части каждого из предыдущих тождеств на dx, мы получим из соотношений между дифференциалами соотношения между производными; например, последнее соотношение дает

(u/v)’=(vu’-uv’)/v²

Дифференцирование простейших функций приводит к следующим результатам: d(x^m)=mx^m-1dx при всяком действительном m, d sinx = cosх dx, d cosx = — sinx dx, d tgx = dx/cos²x,  d ctgx = - dx/sin²x, arcsinx = dx/√(1-x²), d arccosx = - dx/√(1-x²), d arcctgx = dx/(1+x²), d arcctgx = - dx/(1+x²), de^x = e^xdx, da^x = a^x loga dx, d logx = (dx/x)d, log_ax = dx/xloga.

Пусть теперь у представляет сложную функцию от х, т. е. пусть у зависит не непосредственно от х. а от некоторого переменного и, которое есть само функция от x. Если, например, у = sin²х, положив sinx = u представим у в виде у = u², и у будет сложной функцией от х. Правило дифференцирования сложной функции выражается формулой dy = (dy/du)du или ей равносильной dy/dx = dy/du∙du/dx, т. о., производная сложной функции равна производной от этой функции по тому переменному, от которого она непосредственно зависит, умноженной на производную от этого переменного по переменному независимому. Например, применяя это правило к функции у = sin²x, и полагая sinx = u, найдем d sin²x/dx = d(u²)/dx = d(u²)/du∙du/dx = 2u(d sinx/dx) = 2 sinx cosx.

Первоначально думали, что всякая непрерывная функция имеет производную, подобно тому, как всякая непрерывная кривая имеет касательные и всякое непрерывное движение имеет скорость. Ошибочность этого мнения выяснилась только из исследований Римана (1854). В 1861 г. Вейерштрасс дал пример функции непрерывной при всех значениях аргумента и не имеющей производной ни при одном из этих значений.

Основную теорему дифференциального исчисления представляет теорема конечных приращений, состоящая в следующем. Если для всех значении аргумента х, от х = а до х = b, функция f(х) конечна, (не обращается в бесконечность), непрерывна и имеет определенную производную f'(х), то между а и b есть по крайней мере одно значение х=с, для которого

f(b) — f(а) = (Ь — а) f'(с), или [f(b)-f(a)]/(b-a) = f'(с).

Из этой теоремы получаются все важнейшие предложения дифференциального исчисления. Ее значение состоит в том, что ей устанавливается связь между конечными приращениями функции и аргумента, с одной стороны, и производной, т. е. отношением бесконечно малых приращений, с другой.

Черт. 3.

Теореме конечных приращений можно дать простое геометрическое истолкование. Пусть будет f(х) уравнение кривой MN (черт. 3). Пусть будет ОА = а, OB = b абсциссы точек M, N, OC = c – абсцисса точки Р. Тогда AM = f(a), BN = f(b), и отношение [f(b)-f(a)/(b-a)] представляет tg OMN, т. е. tg угла наклонения хорды MN к оси х. Точно так же f'(с) есть tg угла наклонения касательной в точке Р к оси х. Таким образом теорема конечных приращений выражает, что на всякой дуге есть, по крайней мере, одна точка, касательная в которой параллельна хорде, соединяющей концы дуги.

Так как производная от функции есть сама также функция того же переменного, то от производной можно ваять новую производную и т. д. Таким образом получаются производные высших порядков, или высшие производные у''=(у')', у'''=(у'')' и т. д., или, по Ньютону, ỳ, ... Так же получаются и дифференциалы высших порядков d²у = d (dy), d³у = d (d²у)... Чтобы найти связь между производными и дифференциалами высших порядков, представим производную у' как отношение дифференциалов dy/dx; дифференцируя это отношение, как дробь, получим

dy' = (d²у dx — d²х dy)/(dx)²

Но dy'/dx = y'', поэтому

y'' = (d²у dx — d²х dy)/(dx)³. Так как мы видели выше, что дифференциал dx есть произвольная величина, то мы можем упростить последнее выражение, условившись считать, что дифференциал независимого переменного есть величина постоянная; так это всегда и принимается в анализе. Тогда d²х, как дифференциал постоянного, равна нулю, и выражение для у'' принимает по сокращении на dx вид у''=d²y/dx²; дальнейшее дифференцирование дает y'''=d³y/dx³, и т. д. Отсюда получаются выражения для дифференциалов высших порядков: d²у = y'' dx², d³у=у'''dx³...

Выражения производных высших порядков для большей части элементарных функций довольно сложны; но для некоторых функций можно дать общие выражения их производных высших порядков. Так, обозначая производную n-го порядка от y через y⁽ⁿ⁾, будем иметь

Замечательна также формула Лейбница, дающая выражение высших производных от произведения

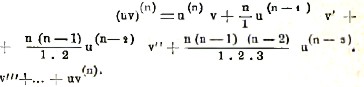
Функции от нескольких независимых переменных также имеют производные и дифференциалы. Если, например, мы имеем функцию трех переменных u=f(х, у, z), то мы можем исследовать изменение u в зависимости от изменения каждого из трех переменных х, у, z в отдельности; при этом всякий раз мы предполагаем изменяющимся только одно из независимых переменных, тогда как остальные переменные остаются без изменения. Таким образом, мы получаем т. н. частные производные от данной Функции по каждому из независимых переменных отдельно. В нашем случае мы будем иметь три частных производных, составленных в предположении, что изменяется только одно из трех переменных.

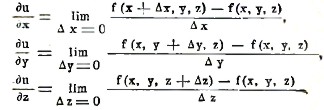
Если, например, мы имеем функцию двух переменных u = x^y, то найдем следующие выражения для двух частных производных (см. выше формулы дифференцирования):

Обозначение частных производных в виде ∂u/∂x, ∂u/∂y, ∂u/∂z, принадлежит Якоби. Оно отличается от приведенного выше обозначения обыкновенной производной dy/dx введением круглого ∂ вместо d.

Такое различие должно напоминать, что тогда как в обыкновенной производной dy/dx дифференциалы dy, dx имеют самостоятельное значение, - в выражении частной производной ∂u/∂x числитель и знаменатель отдельно значения не имеют. Умножая частные производные на соответствующие дифференциалы переменных dx, dy, dz, получаем частные дифференциалы.

Полным дифференциалом функции называется сумма ее частных дифференциалов

Если функция u — сложная, т. е. зависит от переменных r, s, t, которые сами зависят от х, у, z, то выражение полного дифференциала остается то же

причем dr, ds, dt суть сами полные дифференциалы; например,

Вставлял вместо dr, ds, dt их выражения и собирая коэффициенты про dx, dy, dz получим выражения частных производных, от сложной функции, например

Последовательное дифференцирование приводит к частным производным высших порядков. Например, функция u от двух переменных х, у имеет четыре частных производных второго порядка

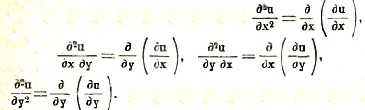
Основное свойство частных производных высших порядков состоит в том, что они не зависят от порядка дифференцирования, например, ∂²u/∂x∂y = ∂²u/∂y∂x. В выше приведенном примере u = x^y, дифференцируя полученные выражения для

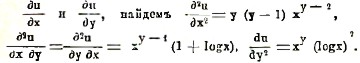
Из правил дифференцирования функции нескольких переменных выводится правила дифференцирования неявных функций (см. функция). Пусть у определяется, как неявная функция от х, уравнением φ (х, у) = 0. Дифференцируя обе части по х и имея ввиду, что у есть функция от х, получаем по правилу дифференцирования сложных функций ∂φ/∂x∙∂x/∂x + ∂φ/∂y∙∂y/∂x, и отсюда, так как dx/dx = 1, находим выражение производной неявной функции в виде

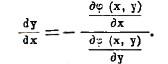
Если, например, у связано с х уравнением х²—у³—1 = 0, то мы получим dy/dx = 2x/3y². Очевидно, что если х дано, то у нельзя здесь брать произвольно, а необходимо брать для у то значение, которое вместе с взятым значением х удовлетворяет уравнению φ(х, у)=0. Таким же образом получаются и частные производные от неявных функций нескольких переменных. Например, рассматривая в уравнении x²+y²+z²-1=0 z как неявную функцию от х, у и дифференцируя по х, найдем 2х+2z(∂z/∂x)= 0, откуда ∂z/∂x = -x/z. Наконец, многократным дифференцированием получаются таким же образом производные высших порядков. Пусть, например, z' определено как неявная функция от х, у уравнением х⁴у³z²=1; и требуется найти ∂²z/∂x∂y. Найдем сначала производные первого порядка. Дифференцируя данное уравнение по х и по у, находим

4х³y³z² + 2х⁴у³z (∂z/∂x) = 0, 3х⁴y²z² + 2х⁴у³z (∂z/∂y) = 0, или по сокращении

2z + x(∂z/∂x) = 0, 3z + 2y(∂z/∂y) = 0. Дифференцируя затем первое из полученных уравнений по у, находим 2(∂z/∂y) + x(∂²z/∂x∂y) = 0, или заменяя (∂z/∂y) его выражением из второго уравнения

-3z/y + x(∂²z/∂x∂y) = 0, откуда получаем окончательно ∂²z/∂x∂y = 3z/xy. Если, например, x=2, y=1, то предложенное уравнение дает для z два значения: z = ±1/4. Этим двум значениям  z будут соответствовать значения производной ∂²z/∂x∂y = ±3/8.

Изложенное здесь представляет, в существенных чертах, теорию дифференциального исчисления. Не касаясь приложений дифференциального исчисления к геометрии и механике (см. соответствующие статьи), мы остановимся здесь на приложениях дифференциального исчисления к анализу. Важнейшие из них состоят в разложении функции в ряды, в изыскании наибольших и наименьших значений функции и в  нахождении главных значений неопределенных выражений.

Пусть мы имеем функцию f(х), которая, вместе с своими производными до (n—1)-го порядка f’(х), f”(x)… f^(n-1)(x) конечна при x=a; пусть, кроме того, n-ая производная f⁽ⁿ⁾(х) имеет определенные значения для всех значений х между а и а+h. Тогда, применяя теорему конечных приращений (см. выше), можно вывести формулу Тейлора:

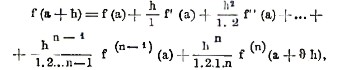
где θ - некоторое число, содержащейся между нулем и единицей. Последний член называется остаточным членом формулы Тейлора. Эта формула представляет обобщение теоремы средних приращений. Независимо от своего теоретического значения, эта формула может служить для приближенного вычисления функций. Если остаточный член настолько мал, что при данной точности вычислений им можно пренебречь, то зная значение функций и ее n—1 производных при х=а, мы можем вычислить значения функций для всех достаточно близких значений х=а+h. Если при неограниченном возрастании и остаточный член стремится к нулю, то в формуле Тейлора разложение может быть продолжено неограниченно, и мы получаем  разложение функции в бесконечный ряд Тейлора (Taylor, 1715, Joh. Bernoulli, 1694):

Отсюда при а = 0, заменяя h через х, получаем рад Маклорена (Maclaurin, 1742):

Этот ряд определяет функцию f(х) по значению функции и ее производных, при х=0, для всех значений х, для которых этот ряд сходящийся (см. ряды). Он дает разложение функции по целым положительным степеням аргумента, и, следовательно, представляет функции при помощи элементарных действий, умножения и сложения, и, кроме того, переход к пределу.

Подставляя в ряд Маклорена вместо f(х) различные функции, получаем их разложения в ряды; при помощи этих разложений удобно исследовать свойства функций, а также вычислять их значения. Ряды для sinx и cosx даны в ст. высшая математика. Из других рядов укажем на следующие:

(бином Ньютона);

Заменяя в разложении е^х х через iх, где i=√-1, получаем знаменитое соотношение Эйлера (1748): е^ix = cos х + i sin х, связывающее показательную функцию с тригонометрическими. Эта формула позволяет определить показательную функцию е^х для мнимых значений аргумента. Заменяя в формуле Эйлера снова х через iх, получаем е^х = cos iх + i sin iх, и меняя знак при х, е^х = соs iх — i sin ix.

Отсюда cos iх = (e^x+e^-x)/2 , sin iх = i(e^x-e^-x)/2  , формулы, определяющие тригонометрические функции для мнимых значений аргумента.

Ряд Тейлора может быть распространен на функции нескольких переменных. Например, для функции двух переменных он имеет вид:

Из формулы Тейлора можно вывести способы определения наибольших и наименьших значений — maxima и minima — функций. Под maximum и minimum, в собственном смысле, разумеются наибольшее и наименьшее из всех значений, которые может принимать данная функция. Но в анализе под maximum разумеют обыкновенно такое значение функции, которое больше всех близких значений той же функции, т. е. значений, соответствующих достаточно близким значениям аргумента. Другими словами, функция f(х) имеет maximum при х=а, если разность f(а)-f(а+h) положительна при всех достаточно малых значениях b, положительных и отрицательных; точно так же функция f(х) имеет minimum при х=а, если разность f(а)-f(а+h) отрицательна при всех достаточно малых значениях h. Например, функция у = (х²—1)² (черт. 4) имеет два minima при х=±1, так как при этих значениях она обращается в нуль, а при всех других она положительна. С другой стороны, она имеет maximum при х=0, причем этот maximum равен единице, хотя при других значениях х, например, при х=3/2, у получает значение 25/16 большее единицы. Значение функции при х=0 представляет maximum не потому, что оно больше всех остальных значений функции, а потому, что оно больше значений функции, при значениях аргумента х, близких к нулю. Действительно, при всяком х, близком к нулю, значение функции, очевидно, меньше ее значения при х=0, т. е. единицы, и потому значение у=1, соответствующее х=0, есть maximum.

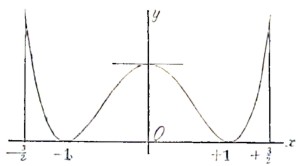
Черт.4

Возьмем формулу Тейлора, останавливаясь на втором члене: f(а+h) - f(а) = h [f’(а) + (h/2)f’(а+θh)].

Она показывает, что функция f(х) будет иметь при x=a maximum или minimum только в том случае, если f’(а) = 0; иначе с переменой знака у h разность f(а+h) - f(а) будет также менять знак, и мы не будем иметь ни maximum, ни minimum. Геометрически это значит, что в тех точках кривой, где ее ордината достигает maximum или minimum, касательная к кривой должна быть параллельна оси х. Положим, что при х=а производные f'(а), f''(а)... f^(n-1) (а) обращаются в нуль, а f⁽ⁿ⁾(а) равно нулю. Тогда формула Тейлора, дает

f(a+h)-f(a) = hⁿ/1,2…n[f⁽ⁿ⁾(a)+h/(h+1)f⁽ⁿ⁺¹⁾(a+θh]

Отсюда видно, что maximum или minimum будет только при n четном, и притом maximum будет, если f⁽ⁿ⁾(a) отрицательно, а minimum — если f⁽ⁿ⁾(a) положительно. Таким образом, чтобы функция f(х) имела при х=а maximum или minimum нужно, чтобы низшая производная, не обращающаяся в нуль при х=а, была четного порядка; если значение этой производной отрицательно, то мы имеем maximum; если положительно — minimum. В приложениях вопрос решается обыкновенно знаком второй производной. В предыдущем примере у = (х²—1)², или у = х⁴ — 2х² + 1, для определения maxima и minima составляем производную у' = 4х³ — 4х. Функция может иметь maxima и minima только при тех значениях х, при которых первая производная равна нулю; решая уравнение 4х³-4х=0, находим три корня: х = 0, х = ±1. Чтобы узнать, соответствуют ли этим значениям maxima или minima, составляем вторую производную у'' = 12х² — 4. Так как эта производная отрицательна при х = 0 и положительна при х = ±1, то значению х = 0 соответствует maximum, а значениям Х = ±1 — minima данной функции. Найдем еще прямоугольник, который при данном периметре имел бы наибольшую площадь. Обозначим периметр прямоугольника через 2а, его основание через х. Тогда высота прямоугольника будет а—х, а его площадь s = х(а— х), или s=ax—х². Чтобы найти maximum s, составляем первую и вторую производные от s по х, s'= а—2х, s'' = —2. Приравнивая нулю первую производную, находим x=a/2, а так как вторая производная отрицательна, то полученное значение дает, действительно, maximum площади s. Из x=a/2 находим: а—х= a/2,  т. е. высота равна основанию; таким образом из всех прямоугольников с данным периметром наибольшую площадь имеет квадрат.

Формула Тейлора применяется также к нахождени главных значений неопределенных выражений. Если в дроби φ(x)/f(x) обе функции обращаются при х=а в нуль, то при этом значении переменного эта дробь не имеет определенного числового значения; но мы можем искать предел, к которому стремится эта дробь, когда х неограниченно приближается к а; такой предел,

lim φ(x)/f(x)
^х=а

называется главным, или, хотя и неправильно, истинным значением неопределенного выражения. Полагая х = a+h и разлагая числитель и знаменатель по формуле Тейлора будем иметь:

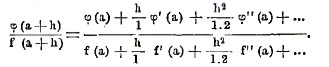
По предположению φ(а) = 0, f(а) = 0. Сокращая в правой части на h и переходя к пределу, получим

Найдем, например, главное значение дроби (2e^x-x²-2)/(x-sin x)  при х = 0. Заменяя числитель и знаменатель их производными, до тех пор, пока по крайней мере один из них не сделается при х=0 отличным от нуля, найдем:

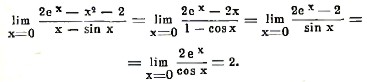
III. Интегральное исчисление. В  дифференциальном исчислении мы по данной функции ищем ее производную или еле дифференциал. Обратно, имея данную производную f(х) или дифференциал, мы можем искать ту начальную функцию F(х), которой соответствует эта производная или этот дифференциал. Эта начальная функция изображается по Лейбницу в виде ∫f(х)dx, так что равенство F(х) = ∫f(х)dx равносильно dF(х) = f(х)dx, или F'(х)=f(х). Из определения интеграла следует: d ∫ udx = udx, ∫ du=n+С, где С — произвольное постоянное. Переход от данного дифференциала к начальной функции называется интегрированием, а самая начальная функция — интегралом. Интегральное исчисление исследует свойства интегралов и способы их вычисления (см. высшая математика). Из указанного выше геометрического и механического значения производной следует, что интегрированием решается, между прочим, задача о нахождении кривой по данному направлению касательных в различных ее точках, а также задача о вычислении пути, пройденного движущейся точкой по данному закону изменения ее скорости. Первая задача интегрального исчисления — нахождение начальной функции по данному ее дифференциалу. Очевидно, что некая формула дифференцирования дает соответствующую формулу интегрирования. Таким образом, из приведенных выше дифференциальных формул получаем следующие формулы интегрального исчисления:

 ∫Сudx = C ∫udx,

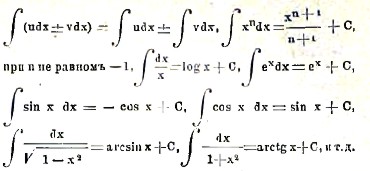
Такое интегрирование, когда выражение интеграла прямо получается из соответствующих формул дифференциального исчисления, называется непосредственным  интегрированием и возможно, конечно, только в простейших случаях. В тех случаях, где оно неприменимо, интеграл иногда может быть получен посредством вспомогательных приемов, из которых  главнейшие: разложение на слагаемые, интегрирование посредством подстановки и интегрирование по частям. Первый прием состоит в разложении подынтегральной функции на слагаемые, каждое из которых интегрируется проще, чем вся сумма, например

∫(4x+5)dx = ∫4xdx + ∫5dx = 2x²+5x+C. Второй прием заключается в том, что вместо независимого переменного — переменного интеграции — вводят новое переменное, причем при надлежащем выборе подстановки преобразованный интеграл находится более просто, чем первоначальный. Например, полагая в интеграле ∫dx/(2x-1), x=(y+1)/2, получим 2х—1 = у, dx=dy/2, и данный интеграл обратится в ½∫dy/y, который интегрируется непосредственно и дает ½ logy + C. Подставляя вместо у его выражение через х, у = 2х—1, получаем искомый интеграл в виде

∫dx/(2x-1) = ½ log(2x-1) + C

Интегрирование по частям основано на следующем дифференциальном соотношении (см. выше): d(uv) = udv+vdu. Отсюда, интегрируя, получаем ∫udv = uv - ∫vdu. Таким образом, интегрирование дифференциала udv приводится к интегрированию дифференциала vdu, которое может оказаться более простым.

Найдем, например, ∫х cosx dx. Полагая х=u, cosx dx = dv, получим du=dx, v=sinx, и формула интегрирования по частям дает ∫х cosх dx =  х sinx — ∫sinx dx. Последний интеграл находится непосредственно, и мы получим

∫x cosx dx = x sinx + cosx + C.

Применяя одновременно различные приемы, можно вычислять и более сложные интегралы. Найдем, например ∫dx/(x²-1). Разлагая подынтегральную функцию на слагаемые получим

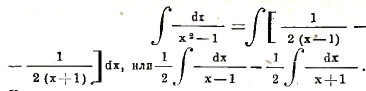
Подставляя в первом интеграле х=u+1, во втором x=v-1, получим ½ ∫du/u – ½ ∫dv/v или ½ log u – ½ log v + C. Заменяя теперь обратно u через x-1  и v через x+1 и пользуясь известными свойствами логарифмов, получим окончательно

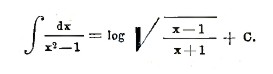
Интегрирование функций весьма редко приводит к функции той же степени сложности. Обыкновенно интеграл сложнее, чем подынтегральная функция. Так, мы видели, что производной 1/x соответствует интеграл log x, функции 1/(1+x²)-arctg x. Таким образом, интегральное исчисление представляет неистощимый источник новых классов функций (см. высшая математика). Только в особенно простых случаях интегралы выражаются в элементарных функциях — алгебраических, показательных, тригонометрических и им обратных. Именно, это бывает тогда, когда под знаком интеграла стоит функция рациональная, или функция, содержащая корень квадратный из многочлена первой или второй степени, и, в исключительных случаях, при интегрировании более сложных функций.

Обозначим через F(х) интеграл ∫f(x)dx.

Тогда разность F(b)—F (а) значений интегральной функции, взятых для значений переменного x=b и х=а, изображается в виде ∫_a^b f(х)dx и называется определенным интегралом от f(х); числа а и b называются нижним и верхним пределами определенного интеграла (см. высшая математика). Интеграл ∫f(x)dx называется, в отличие от определенного интеграла ∫_a^b f(х)dx – неопределенным интегралом. Например, имея ∫xdx = x²/2 + C, мы найдем

∫₃⁵xdx = (5²/2 + C) – (3²/2 + C) = 8

Очевидно, что при вычислении определенного интеграла по неопределенному произвольное постоянное всегда исчезает. Так как при вычислении определенного интеграла переменное интеграции х заменяется пределами интеграла а и b, то определенный интеграл не зависит от переменного интеграции х, а только от вида подынтегральной функции f(х) и от пределов интеграции, а и b, так, что

∫_a^bf(x)dx = ∫_a^bf(y)dy.

Далее, из самого определения определенного интеграла непосредственно следуют его основные свойства:

∫_a^af(x)dx = 0, ∫_a^bf(x)dx = - ∫_b^af(x)dx, ∫_a^bf(x)dx + ∫_b^сf(x)dx = ∫_a^cf(x)dx. Если в интеграле ∫_a^bf(x)dx  предел b стремится к бесконечности, то предел интеграла, если он существует, обозначается через

Например, зная, что

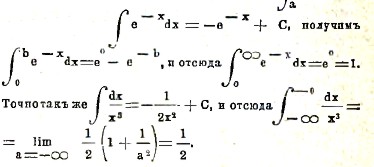
Будем рассматривать в равенстве ∫_a^bf(x)dx  = F(b) – F(a) верхний предел, как переменную величину. Тогда, дифференцируя по b, имеем d/db ∫_a^bf(x)dx = F’(b). Но, по определению F(x), как интеграла ∫f(x)dx имеем F’(x)=f(x). Поэтому, d/db ∫_a^bf(x)dx = f(b).

Таким образом, производная от определенного интеграла по его верхнему пределу равна значению подынтегральной функции на этом пределе.

Каждый неопределенный интеграл всегда можно представить в виде интеграла определенного, так как из

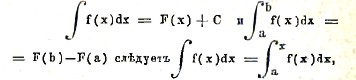
где а — постоянное, выбранное под условием F(а)=—С.

Так как главная задача интегрального исчисления состоит в определении начальной функции по ее производной, то интегральное исчисление представлять исчисление обратное дифференциальному. Но интегральное исчисление имеет и самостоятельное значение. Как в дифференциальном исчислении производная есть предел отношения двух бесконечно малых величин, так в интегральном исчислении определенный интеграл представляет предел бесконечно большого числа бесконечно малых слагаемых, т. е. предел, к которому стремится сумма, когда слагаемые неограниченно уменьшаются, а их число неограниченно возрастает. Именно, в интегральном исчислении доказывается следующее свойство определенного интеграла. Пусть мы имеем функцию f(х), непрерывную при изменении х в некотором промежутке. Возьмем в этом промежутке два числа а и b, причем пусть, например, b>а. Поместим между а и b ряд возрастающих чисел a₁, a₂, ... а_n и рассмотрим сумму f(а)(а₁-а) + (а₁) (а₂-а₁) + .... + t(а_n) (b-а_n). В этой сумме каждое слагаемое равно разности двух последовательных чисел а, умноженной на значение функции f(х) при втором из этих значений. Будем беспредельно увеличивать число промежуточных значений, так чтобы все их разности беспредельно убывали. Тогда оказывается, что предел, к которому стремится написанная сумма, есть не что иное, как определенный интеграл ∫_a^bf(x)dx. С этим свойством определенного интеграла связан и символ ∫, введенный для Лейбницем: этот символ происходит от буквы S, начальной буквы слова summa. Cимвoл ∫(х)dx представляет, по его первоначальному смыслу, сумму бесконечно большого множества бесконечно малых слагаемых f(х)dx, каждое из которых есть произведение значения функции f(х), на dx — бесконечно  малое приращение независимого переменного х.

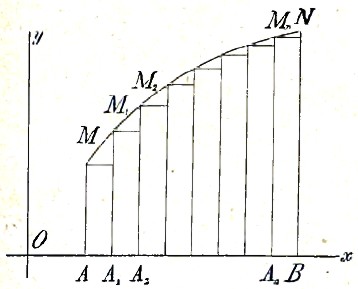
Черт. 5

Рассматривая определенный интеграл, как предел суммы, мы можем дать ему простое геометрическое истолкование. Пусть мы имеем кривую у = f(х) (черт. 5). Найдем выражение площади, ограниченной этой кривой, осью х и двумя ординатами AM, BN, восстановленными в точках х=а, х=b. Поместим между точками А, В, ряд точек А₁, А₂, ... А_n с абсциссами a₁, а₂, ... а_n и построим на полученных отрезках прямоугольники, высотами которых служили бы ординаты соответствующих точек кривой. Очевидно, что сумма площадей этих прямоугольников будет весьма мало отличаться от искомой площади кривой AMNB, и что по мере того, как число точек деления будет  увеличиваться, разность между площадью кривой и суммой площадей прямоугольников будет без предельно уменьшаться. Так как сумма площадей прямоугольников равна AM.AA₁ + A₁M₁.А₁А₂ + ... , или f(а)(а₁—а) + f(а₁)(а₂—а₁) + ... + f(а_n)(b—а_n), то площадь кривой будет равна пределу этой суммы, т. е. равна ∫_a^bf(x) dx. Таким образом, определенный интеграл ∫^bf(x) dx представляет геометрически площадь, ограниченную кривой y=f(x).

Так как вычисление площадей криволинейных фигур называется квадратурой, то и вычисление функции по ее производной или дифференциалу, т. е., интегрирование, получило в анализе то же самое название, так что квадратура и интегрирование функции — два равносильных термина.

Определенный интеграл имеет также простое механическое значение. Пусть точка движется в течение промежутка времени от t=а до t=b, причем скорость движения представляет определенную функцию времени f(t). Разобьем промежуток времени между t=а и t=b на части промежуточными моментами t = a₁, t = a₂,..t = a_n и предположим, что в течение каждого промежутка движение происходит равномерно, с постоянной скоростью, так что скорость движения меняется не непрерывно, а скачками в конце каждого весьма малого промежутка времени, на которые мы разбили весь промежуток от t = а до t = b. Так как в равномерном движении пройденный путь измеряется произведением скорости на время движения, то весь путь, пройденный таким образом, выразится суммой

f(a)(a₁-a) + f(a₁)(a₂-a₁) +…+ f(a_n)(b-a_n).

Этот путь не равен искомому, потому что в заданном движении скорость изменяется непрерывно, тогда как у нас она меняется скачками; но если промежутки времени будут уменьшаться, эти скачки будут все меньше и меньше, и в пределе мы получим истинный пройденный путь. Таким образом, если скорость движения выражается функцией f(t), то путь, пройденный от момента t = а до t= b, выразится определенным интегралом ∫_a^bf(t) dt. Найдем, например, путь, пройденный во время t телом, падающим под действием тяжести, если известно, что скорость падения выражается формулой v = gt, где g — постоянное. Тогда пройденный путь будет

S = ∫₀¹gt dt.

Неопределенный интеграл

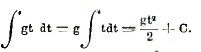
Подставляя пределы интеграции, найдем s = gt²/2 – 0 = gt²/2.

Хотя при данном виде подынтегральной функции интеграл зависит только от  пределов интегрирования, и, при постоянных пределах, сам есть величина постоянная, но, если подынтегральная функция, содержит, кроме переменного интеграции, еще другие переменные, т. н. параметры, то интеграл сам будет функцией этих параметров. Так, например,   мы имеем

Таким образом, интеграл

хотя его приделы постоянны, представляет переменную величину, функцию переменного параметра р. Некоторые из функций, выражаемых определенными интегралами, обладают особыми свойствами. Так, есть определенные интегралы, значение которых, при непрерывном изменении параметра, изменяются прерывно, скачками. Например, интеграл

∫₀^∞sinpx/x dx равен π/2 при р > 0, -π/2 при р < 0 и нулю при р = 0; здесь π есть отношение окружности к диаметру.

Если мы имеем функцию нескольких переменных, то, интегрируя ее последовательно по каждому из переменных, мы получим кратный интеграл; при этом в каждом из последовательных интегрирований все переменные, кроме того, по которому интегрирование производится, рассматриваются, как постоянные. Если ищется определенный кратный интеграл, то пределы каждого интегрирования могут быть или постоянными или зависеть от всех тех  переменных, по которым интегрирование еще не было произведено. Найдем, например,

который обыкновенно изображается в виде

 Чтобы вычислить это выражение, нужно проинтегрировать х + у + z по z между пределами 0 и х + у, затем полученное выражение проинтегрировать по у от 0 до х и, наконец полученный результат проинтегрировать по х от 0 до 1.

Первое интегрирование даст xz+yz+z²/2+φ(x,y), где φ(х, у), произвольная функция от х, у, стоит на месте произвольного постоянного, входящего в неопределенный интеграл. Это потому, что при интегрировании по z остальные переменные  х, у рассматриваются как постоянные, и следовательно, всякая функция от х и у представляет по отношению к z постоянную величину. Подставляя в неопределенный интеграл пределы 0 и x+y, получим

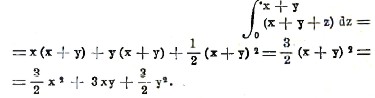
Интегрируя затем полученную функцию по у, получим неопределенный интеграл

3/2x² + 3/2xy² + 1/2y3 + φ(x), где φ(x) – произвольная функция от x. Подставляя сюда пределы 0 и x, получим

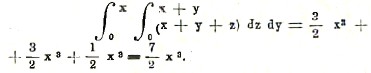
Наконец, интегрируя полученное выражение по x, получим неопределенный интеграл 7/8 x + C и, подставляя пределы 0 и 1, будем иметь окончательно

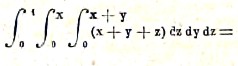 7/8

Когда определенный интеграл нельзя выразить формулой, удобной для вычислений, в приложениях довольствуются приблизительным вычислением интеграла с нужной степенью точности. Применяемые при этом приемы носят название механических квадратур. Простейший из этих приемов есть метод трапеций. Пусть нам нужно вычислить площадь кривой у = f(х) между ординатами х = а, х = b (черт. 6).

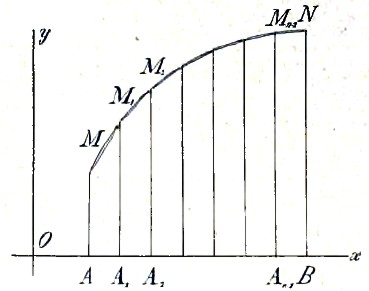
Черт. 6

Эта площадь, как мы видели, представляется интегралом ∫_a^bf(x) dx. Разобьем промежуток  АВ = b-a на n равных частей  — h =  (b-a)/n в точках A₁ , А₂,.. A_n-1,  восставим в каждой точке деления ординаты до пересечения с кривой и соединим концы ординат ломаной линией М M₁ M₂ ... N. При приближенном вычислении мы можем заменить площадь, ограниченную кривой МN, площадью, ограниченной этой ломаной; последняя представляет сумму площадей трапеций с высотами АА₁ = А₁А₂= ... = h. Отсюда, пользуясь формулой площади трапеции, получим приближенное выражение искомого интеграла,

где у₀, у₁, ... суть величины ординат AM, A₁M₁, ... , т. е. значения f(а), f(а₁), f(а₂) ...

Приложения определенных интегралов весьма разнообразны. Так, интегралами пользуются при вычислении длин линий, поверхностей и объемов тел, при определении центров тяжести и моментов инерции, в теории притяжения и мн. др.

IV. Дифференциальные уравнения. Дифференциальными уравнениями называются уравнения, в которые входят переменные, их функции и производные от этих функции. Дифференциальные уравнения делятся на обыкновенные дифференциальные уравнения, или уравнения с одним независимым переменным, например

dy/dx = y² + 2xy + 3x², и уравнения с частными производными, или уравнения с несколькими независимыми, например

∂²z/∂x² + ∂²z/∂y² = 0

Порядком дифференциального уравнения называется высший порядок входящих в него производных. Из приведенных выше двух уравнений одно — первого порядка, а другое — второго.

Функция, удовлетворяющая вместе с своими производными данному дифференциальному уравнению, называется его интегралом, или решением. Изыскание всех функций, удовлетворяющих данному уравнению, называется интегрированием данного уравнения.

Ближайшая задача теории интегрирования дифференциальных уравнений состоит в изыскании способов для приведения интегрирования данного уравнения там, где это возможно, к интегрированию другого дифференциального уравнения, более простого. Самое простое дифференциальное уравнение есть, очевидно, dy/dx = f(х), самое общее решение которого

y = ∫f(х) dx + С получается посредством квадратуры. Задача интегрирования других, более сложных, уравнений считается решенной, когда она также приведена к квадратурам, т. е. к интегрированию известных функций от одного независимого переменного. Самое выполнение квадратур составляет уже задачу собственно интегрального исчисления (см. выше).

Общий вид обыкновенного дифференциального уравнения n-го порядка с одной неизвестной функцией есть f (х, у, у', у''.... у⁽ⁿ⁾) = 0, где левая часть представляет данную функцию от х, у и производных от у по х да n-го порядка включительно. Каждое такое уравнение имеет общее решение, или общий интеграл у = F(x, С₁, С₂... С_n), представляющий определенную функцию от х и от n произвольных постоянных, С₁, С₂... С_n.

Давая в выражении общего интеграла постоянным различные частные значения, получим различные частные интегралы предложенного уравнения. Например, уравнение у'' + у = х имеет общий интеграл у = х+С₁ sin х+C₂ cosx,  удовлетворяющий данному уравнению при всех значениях постоянных С₁ и С₂. Некоторые дифференциальные уравнения имеют, кроме общего интеграла, еще т. н. особые решения, которые не получаются из общего интеграла ни при каких значениях произвольных постоянных. Например, уравнение первого порядка у = ху'—у'² имеет, кроме общего интеграла у = Сх—С², еще особое решение у = x²/2.

В случае дифференциальных уравнений первого порядка соотношение между общим интегралом и особым решением имеет весьма простое геометрическое истолкование. Общий интеграл у = F(х, С) представляет семейство кривых, члены которого соответствуют различным значениям параметра С; особое решение представляет огибающую этого семейства, т. е. кривую, касательную ко всем линиям, изображаемым общим интегралом. Так, в предыдущем примере, общий интеграл у =  Сх—С₂ представляет семейство прямых, соответствующих различным значениям постоянного С, а особое решение у = x2/2 — параболу (см. высшая математика), касающуюся всех этих прямых (черт. 7).

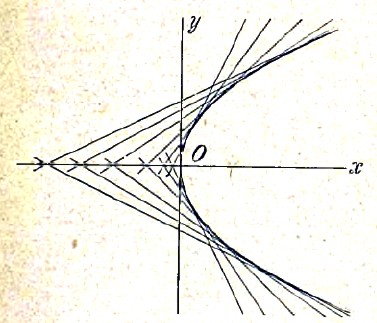
Черт. 7

Всякое дифференциальное уравнение первого порядка можно всегда привести к виду dy/dx = f(х, у), решив его относительно производной; но, для сохранения симметрии между обоими переменными х и у, ему обыкновенно дают вид Mdx + Ndy = 0, умножая обе части предыдущего уравнения на  M dx и перенося все в первую часть. Здесь М и N суть две  данные функции от х и у. Например, уравнение dy/dx = (x+y)/(x-y)  можно представить в виде (х+у) dx—(х — у) dy = 0; здесь М = х+у, N = — х+у. Уравнение М dx + N dy = 0 интегрируется непосредственно, когда M и N представляют частные производные по х и у от какой-нибудь функции и от х и у, т. е. когда М = ∂u/∂x , N = ∂u/∂y.

В этом случае дифференциальное уравнение обращается в ∂u/∂x dx + ∂u/∂x dy = 0; левая часть представляет теперь полный дифференциал du (см. выше), и потому интеграл уравнений будет ∫du = С, или u = С. Чтобы М и N представляли частные производные от некоторой функции, они должны удовлетворять определенному условию, т. н. условию интегрируемости; дифференцируя первое уравнение по у, а второе по х, получим  ∂M/∂y = ∂²u/∂x∂y, ∂N/∂x = ∂²u/∂x∂y, откуда следует условие интегрируемости ∂M/∂y = ∂N/∂x. Можно показать, что если это условие удовлетворено, то функция u находится по данным М и N посредством двух квадратур. Таким образом, в этом случае интегрирование уравнения первого порядка приводится к квадратурам. Например, в уравнении ydx+xdy = 0 имеем М = у, N = х, и условие интегрируемости удовлетворяется, так как ∂M/∂y = ∂N/∂x = 1.

Не трудно видеть, что  M = ∂(xy)/∂x, N = ∂(xy)/∂y, так что здесь u = ху; следовательно, общий интеграл будет ху = С, или у = C/x. Простейший случай, когда условие интегрируемости удовлетворяется, — тот, где переменные, как говорят, разделены, т. е. когда М зависит только от х, а N только от у. Действительно, в этом случае, ∂M/∂y = ∂N/∂x = 0, и общий интеграл будет

∫M dx + ∫N dy = C.

Например, уравнение x dx + y dy = 0 имеет общий интеграл x2/2 + y2/2 = C. Так как произвольное постоянное мы можем обозначить вместо С, через С/2, то этот общий интеграл можно представить также в более простом виде х² + у² = С.

В тех случаях, когда М и N не удовлетворяют условию интегрируемости, для каждого уравнения первого порядка существуют множители, обращающие М и N в частные производные от некоторой функции и приводящие таким образом интегрирование уравнения к предыдущему случаю. Такой множитель называется интегрирующим множителем, или просто множителем данного уравнения. Например, уравнение ху’—у=2х³, или (у + 2х³) dx — x dy = 0 имеет множитель -1/x².

Действительно, по умножении на этого множителя уравнение принимает вид (xdy – ydx)/x² — 2x dx = 0. Первое слагаемое представляет полный дифференциал от y/x, а второе от –x² (см. выше). Следовательно, левая часть уравнения обращается в d(y/x – x²), и общий интеграл предложенного уравнения получается в виде y/x – x² = C или y = Cx + x³.

Простейшие уравнения первого порядка, интегрирование которых приводится к квадратурам, суть уравнения однородные, уравнения линейные и уравнения Клеро (Clairaut). Уравнения однородные суть уравнения, приводимые к виду dy/dx = f(y/x), где f(y/x) – данная функция от частного y/x; подстановкой y = ux, где u – новая неизвестная функция, уравнение приводится к виду, в котором переменные разделяются. Например, уравнение (x+y) dx – (x-y) dy = 0 (см. выше) приводится к виду

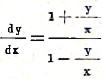
и, следовательно, есть уравнение однородное. Полагая y=ux, преобразуем это уравнение в

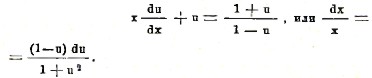
Здесь переменные разделены, и мы имеем интеграл уравнения в виде

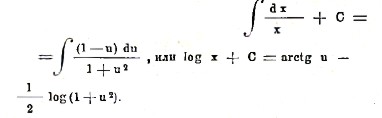
Заменяя здесь u его выражением y/x, получим интеграл предложенного уравнению в виде

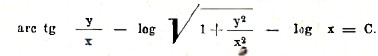
Линейным уравнениям называется уравнение вида dy/dx + Py = Q, где P и Q – данные функции от x. Его общий интеграл есть

 Например, в уравнении xy’ – y = 2x² (см. выше) имеем P = -1/x, Q = 2x², и отсюда общий интеграл

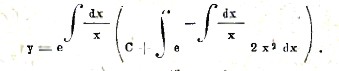
Так как одно из значений определенного интеграла

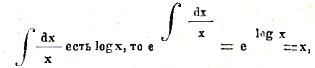
и потому имеем y = x(C + ∫2x dx) или y = Cx + x³. Уравнение Клеро имеет вид y = xy’ + f(y’); его общий интеграл есть y = Cx + f(C). Таково, например, уравнение y = xy’ – y² (см. выше) с общим интегралом y = Cx – C².

Интегрирование дифференциальных уравнений высших порядков, т. е. приведение их к квадратурам, возможно также только в немногих случаях. Обычный способ интегрирования уравнений высших порядков состоит в понижении их порядка, т. е. интегрирование данного уравнения стараются свести, когда это возможно, к интегрированию  нескольких уравнений низших порядков. Если, например, мы имеем уравнение n-го порядка f(х, у’,у’’.... у⁽ⁿ⁾)=0, в которое не входит искомая функция, а только ее производные, то, положив у'=u и приняв u за новую неизвестную функцию, найдем у”=u’,..y⁽ⁿ⁾ = n^(n-1). Произведя эту замену, мы получим, что интегрирование данного уравнения n-го порядка приведено к интегрированию уравнения (n-1)-го порядка f(x, u, u’,.., u^(n-1)) = 0 с неизвестной функцией u и к последующему интегрированию уравнения первого порядка y’=u с неизвестной функцией y.

Из дифференциальных уравнений высших  порядков особенно замечательны уравнения линейные, часто встречающиеся в механике и математической физике. Общий вид линейного уравнения n-го порядка следующий:

где Р₁ ... Р_n и Q —данные функции независимого переменного х. Интегрирование этого уравнения приводится, как будет показано ниже, к интегрированию более простого линейного уравнения, в котором Q=0:

т. н. однородного линейного уравнения, или уравнения без второй части. Лагранж показал, что общий интеграл такого уравнения имеет вид

y = C₁y₁ + C₂y₂ +…+ C_ny_n,

где y₁, y₂ ... y_n известные функции от х₁, а C₁, C₂...,С_n — произвольные постоянные. Например, общий интеграл уравнения 2-го порядка

есть у = C₁X + С₂е^х , как это можно проверить подстановкой.

Линейное однородное уравнение легко интегрируется в том случае, когда все коэффициенты Р — постоянные числа. В этом случае, как показал Эйлер, достаточно найти корни «решающего уравнения»

tⁿ + P₁t^n-1 + P₂t^n-2+..+ P_n-1 + P_n = 0.

Если все эти корни действительны и различны, то, обозначая их через t₁,  t₂... t_n, мы получим общий интеграл предложенного линейного уравнения в виде

Если среди корней решающего уравнения есть мнимые, например, t₁ = α+iβ, t₂ = α-iβ, где i = √-1, то соответствующие члены общего интеграла заменяются через С₁e^αtsin βt + С₂e^αtcos βt. Наконец, если решающее уравнение имеет равные корни, например, t₁ = t₂ = t_p, то соответствующие члены интеграла обращаются в

Найдем, например, общий интеграл уравнения d²y/dx² + a²y = 0, встречающегося в теории колебательных движений. Решающее уравнение будет в этом случае t² + а² = 0, и его корни t₁ = + аi, t₂ = —аi. Отсюда находим общий интеграл в  виде у = C₁sinax + C₂cosax .

Когда  общий интеграл линейного уравнения без второй части известен, то нахождению интеграла соответствующего уравнения со второй частью приводится, как показал Лагранж, к квадратурам, при помощи т. н. метода изменения произвольных постоянных. Сущность этого метода выяснится на следующем примере. Выше мы имели общий интеграл уравнения

y” – x/(x-1) y’ + 1/(x-1) y = 0 в виде у = С₁x + C₂e^x. Чтобы получить отсюда интеграл уравнения со второй частью

y” – x/(x-1) y’ + 1/(x-1) y = х—1, предположим, что в предыдущем выражении С₁  и С₂ суть не постоянные, а некоторые функции от х, которые мы выберем так, чтобы получающееся выражение для у удовлетворило предложенному линейному уравнению со второй частью.

Дифференцируя выражение у = С₁x + C₂e^x, в предположении, что С₁ и С₂ суть функции от х, получим y’ = C₁ + C₂e^x + x(dC₁/dx) + e^x(dC₂/dx). Подчиним С₁ и С₂ условию x(dC₁/dx) + e^x(dC₂/dx) = 0; тогда производная y’ примет вид y’ = C₁ + C₂e^x так, как если бы С₁ и С₂ были постоянными. Составляя затем у”, найдем у” = C₂e^x +  (dC₁/dx) + e^x(dC₂/dx). Подставляя эти выражения для у, у', у'' в предложенное уравнение со второй частью, получим после упрощений (dC₁/dx) + e^x(dC₂/dx) = x-1.

Присоединяя сюда предыдущее условие x(dC₁/dx) + e^x(dC₂/dx) = 0, найдем dC₁/dx = -1, dC₂/dx = xe^-x, и отсюда C₁ = c₁—х₁, С₂ = с₂—(х + 1) e^-x; где с₁ и с₂ – новые  произвольные постоянные. Выражение для С₂ получается здесь интегрированием их по частям (см. выше). Подставляя выражения, полученные для C₁ и С₂, в формулу у = С₁ + С₂е^х, будем иметь общий интеграл предложенного уравнения со второй частью в виде

y = c₁х + с₂е^х — x² — x — 1.

Интегрирование уравнения с частными производными представляет, вообще, задачу значительно более сложную, чем интегрирование обыкновенных дифференциальных уравнений. Для уравнений с частными производными первого порядка с одной неизвестной функцией задачу интегрирования всегда возможно привести к интегрированию системы обыкновенных совокупных дифференциальных уравнении с одним независимым переменным. Тогда как общий интеграл обыкновенных дифференциальных уравнений содержит, как было сказано выше, произвольные постоянные, в общий интеграл уравнений с частными производными входят произвольные функции от определенных аргументов. Так, например, общий интеграл уравнения 1-го порядка

y ∂z/∂x – x ∂z/∂y = 0 есть z = φ(x² + y²), где φ – произвольная функция от х² + у². Точно так же общий интеграл уравнения 2-го порядка ∂²z/∂x² = ∂²z/∂y² есть x = φ(x+y) + ψ(x-y), где φ и ψ – две производных функции соответствующих аргументов.

В случае двух  независимых переменных соотношение z = f(x,у) представляет геометрически некоторую поверхность, и интегрирование уравнения с частными производными можно рассматривать, как нахождение поверхности по данным ее дифференциальным свойствам, свойствам касательной плоскости, линий кривизны и т. п. В некоторых случаях, например для всех уравнений первого порядка, интегрирование уравнения с частными производными приводится к интегрированию некоторой системы обыкновенных дифференциальных уравнений. С геометрической точки зрения эти уравнения определяют па искомой поверхности семейство линий, которые Монж (1795) назвал характеристиками данного уравнения с частными производными. Группируя характеристики по тому или другому закону, мы получим различные поверхности, представляющие геометрически решения предложенного уравнения. Так, например, для уравнения x ∂z/∂x + y ∂z/∂y = z, дифференциальные уравнения характеристики будут dx/x = dy/y = dz/z.

Интегрируя их, получим два уравнения характеристики в виде y/x = c₁, z/x = c₂, где с₁ и с₂ произвольные постоянные. При данных значениях с₁ и с₂ эти два уравнения представляют одну из характеристик; в нашем примере это будет прямая. Чтобы получить интеграл предложенного уравнения с частными производными остается взять какую-либо последовательность этих характеристик, т. е. принять одно из постоянных, например, с₂, за произвольную функцию другого: с₂ = φ(с₁). Исключая постоянные из этого соотношения и двух уравнений  характеристик, получим общее решение предложенного уравнения в виде z = x φ(y/x).

Из предыдущего видно, что задача интегрирования, как обыкновенных дифференциальных уравнений, так и уравнений с частными производными разрешима только в сравнительно немногих частных случаях. Однако, можно доказать, что каждое дифференциальное уравнение, обыкновенное или с частными производными, имеет общий интеграл, зависящий от соответствующего числа произвольных постоянных или произвольных функций. Для обыкновенных уравнений эту теорему доказал Коши (1831), для уравнения с частными производными Ковалевская (1875).

Дифференциальные уравнения встречаются во всех приложениях математики. Хотя во многих случаях и невозможно дать точное выражение интегралов дифференциальных уравнений в закопченном виде, но для приложении важно, что эти интегралы можно представлять в виде бесконечных рядов, члены которых убывают настолько быстро, что на практике, при приближенных вычислениях, можно ограничиваться несколькими начальными членами ряда.

По высшему анализу есть много хороших руководств. Для первоначального ознакомления с основами высшего анализа можно указать Лоренца, «Элементы высшей математики», Пернет и Шлифлисс, «Основания высшей математики» Граве, «Энциклопедия математики». Из более подробных руководств — Носсе, «Курс дифференциального и интегрального исчислений», Гурса, «Курс математического анализа», Jordan, «Cours d’Anulyse», Serret, Lcrhbuch des Differential- und Integral rechnung.

Б. Млодзеевский.