Исчисление (Исчисление конечных разностей)
Исчисление конечных разностей
Исчисление конечных разностей есть одна из математических наук, в которой изучаются приращения функций, соответствующие конечным приращениям аргумента. Исчисление конечных разностей во многом аналогично исчислению бесконечно малых и распадается, как и это последнее, на три отдела: составление разностей, что соответствует дифференциальному исчислению, суммирование, — соответствует интегральному исчислению, и теория уравнений в конечных разностях, — соответствует теории дифференциальных уравнений. Но важно заметить, что исчислению конечных разностей, по существу, чуждо понятие непрерывности, являющееся основным в исчислении бесконечно малых. Одним из главнейших применений исчисления конечных разностей является интерполирование. Первое систематическое изложение исчисления конечных разностей принадлежит Тейлору и было опубликовано им в 1718 г. под заглавием «Methodus incrementorum directa et inversa». В 1730 г. появилось сочинение Стирлинга ««Меthodus differentialis, sive tractatus de sommatione et interpolatione serierum infinitorum». В 1800 г. Лакруа издал сочинение «Traité des différences et des séries». Исчислением конечных разностей много занимались Эйлер, Лагранж и Лаплас. Из работ русских математиков наиболее важны труды Чебышева и Маркова.
1. Пусть будет f(х) функция от х; дадим аргументу х какое-нибудь постоянное конечное приращение h и рассмотрим разность f(х+h)—f(х). Эта разность называется конечной разностью первого порядка от функции f(х) и обозначается символом Δf(х) = f (х+h) — f (х). Разность первого порядка есть, вообще, сама функция от х, и, составляя ее разность, мы получим разность второго порядка
Δ2f(х) =Δf(x+h)-Δf(x), и т. д… Δnf(x) = Δn-1f(x+h)- Δn-1f(x).
Например, если
f(x)=x2 и h=1, то Δx2=(x+1)2-x2=2x+1, и
Δ2x2=[2(x+1)+1]-[2x+1]=2.
При составлении разностей удобно пользоваться следующими теоремами. 1) Разность алгебраической суммы равна алгебраической сумме разностей; в самом деле, мы имеем
Δ[f(x)+φ(x)]=[f(x+h)+φ(x+h)]-[f(x)+φ(x)]=Δf(x)+Δφ(x).
2) Разность от постоянного числа равна нулю. Важно заметить, что разность всякой периодической функции от х также равна нулю, если h равно периоду; в самом деле, из самого определения периодической функции с периодом h следует, что f(x+h) = f(х). Например, если f(х) =sinх и h = 2π, то Δsinx = sin (х + 2π) — sinx = 0.
3) Постоянный множитель можно выносить за знак разности. В самом деле, мы имеем
ΔС f(х) = С f(х + h) — С f(х) = С Δ f(х).
Составим теперь разность от произведения двух функций. Обозначим, для краткости,
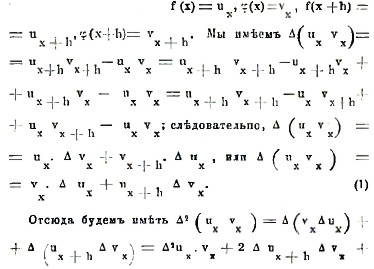
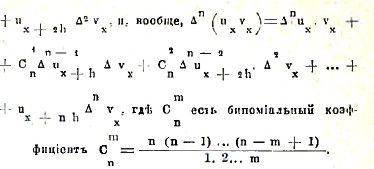
Вычислим разности некоторых простейших функций. Разность от степени xn равна
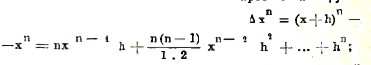
мы видим, что эта разность есть многочлен (n-1)-ой степени; отсюда следует, что Δnxn есть число, независящее от х. Разность от показательной функции ax будет
Δax=ax+h-ax=ax(ah-1), и вообще Δnax=ax(ah-1)n. Разность от логарифма равна
Δlog x = log (x+h) - log x = log (x+h)/x. Разность от sin x представится формулой
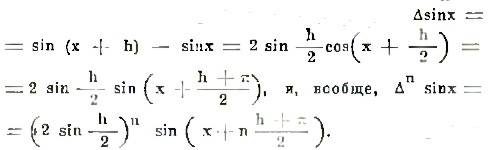
В исчислении конечных разностей важную роль играет функция
f(x) = x(x-h)(x-2h)…[x-(m-1)h]. Эта функция называется факториалом и обозначается символом x(m/h). Разность от факториала есть также факториал; в самом деле, мы имеем
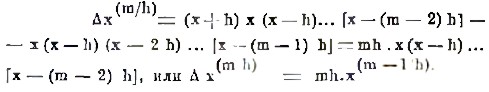
Мы видим, что эта формула вполне аналогична формуле производной от степени дифференциального исчисления. Составляя разности высших порядков от факториала, получим
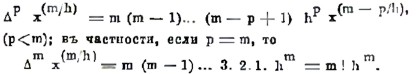
Всякую целую и положительную степень от х можно разложить по факториалам. Для кратнкости возьмем h=1 и обозначим x(k/1) через x(k).
Положим тождественно
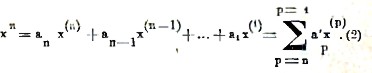
Чтобы вычислить все аР, расположим правую часть тождества (2) по степеням х и приравняем коэффициент при xn единице, а коэффициенты при остальных степенях х – нулю; тогда мы удовлетворим предыдущему тождеству и вместе с тем определим все числа аР. Эти числа аР можно представить следующим образом. Взяв от обеих частей тождества (2) разность р-го порядка и положим затем х=0, мы увидим, что все члены в правой части, за исключением содержащего коэффициент аР, обратятся в нуль, и мы будем иметь
![]()
Введем для
![]()
символическое обозначение ΔР0n; тогда аР=1/Pl ΔР0n, и формула (2) принимает вид
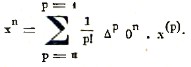
Числа ΔР0n называются числами Бринклея. Легко видеть, что при p>n все ΔР0n равны нулю. Вот значения первых из этих чисел:
![]()
Таким образом, мы имеем
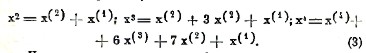
Частным производным дифференциального исчисления в исчислении конечных разностей соответствуют частные разности. Если мы имеем функцию, например, двух независимых переменных f(х,у), то ее частной разностью по х называется выражение
Δх f(х, у)=f(х + h,у)-f(х, у);
так же определяется частная разность по у:
Δу f(x, у)=f (х, у+k)— f (х, у),
причем приращение переменного у может быть уже другим, чем приращение переменного х. Составляя разности второго порядка Δу Δх f и Δх Δу f получим
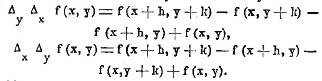
Мы видим, что Δу Δх f = Δх Δу f, т. е. значение разности не зависит от порядка, в котором она вычисляется. Поэтому эту разность обозначают короче символом
Δx,y1+1f(x, y), и, вообще символ Δx,ym+nf(x, y), обозначает частную разность от функции f(x, y), взятую m раз по х и n раз по y в каком угодно порядке.
Разность Δf(х) выражается через производные f’(х), f”(х), ... В самом деле, мы имеем по формуле Тейлора (см. исчисление бесконечно малых)
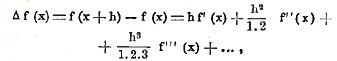
или, в обозначении Лейбница,
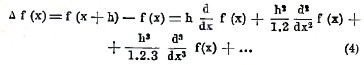
Так как eω=1 + ω + 1/1.2 ω2+ 1/1.2.3 ω3 +… (см. исчисление бесконечно малых), где е – неперово число, то из формулы (3) видно, что операция Δ связана с операциями d/dx, d2/dx2,… символической формулой
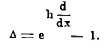
Выведем теперь весьма важную формулу, связывающую значение функции f(х+nh) с значением f(х) и разностями Δ f(х), Δ2 f(х),... до n-го порядка включительно. Из определения разности имеем f(х + h) = f(х) + Δ f(х); заменяя здесь х через х + h, получим f(х + 2h) = f(x + h) + Δ f(х + h). Вставляя сюда вместо f(х + h) и Δ f(х + h) их значения, выведенные из предыдущей формулы, мы будем иметь f(х + 2h) = f(х) + 2 Δ f(х) + Δ2 f(х). Если в этой формуле мы заменим х через х+h, то подобно предыдущему получим
f(х + 3h) = f (х) + 3Δ f(х) + 3Δ2 f(х) + Δ3 f(х), и, вообще,
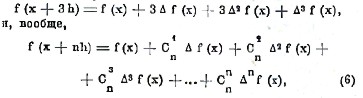
где биноминальные коэффициенты Сn1, Сn2,... имеют значения
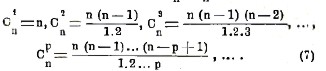
II. Перейдем теперь к изучению суммирования. Задача суммирования заключается в следующем: Определит функцию F(х), разность которой ΔF(х) = F (х + h) — F (x) равна данной функции f(х)
Δ F(х) = F (х+h) — F(х) = f(х). (8)
Если известна одна такая функция, то мы получим все остальные, прибавляя к ней произвольное постоянное или произвольную периодическую функцию от х с периодом h; в самом деле, функции F(х) и F1(х) = F (х) + С имеют одну и ту же разность F (х+h)-F(х). Зная функцию F(х), мы можем удобно вычислить сумму ряда
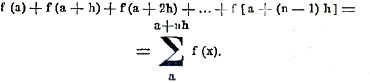
В самом деле, полагая в равенстве (8) последовательно х = а, а + h, а + 2h, ... а + (n—1)h, получим
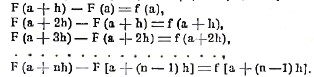
Складывая эти равенства, будем иметь основную формулу суммирования
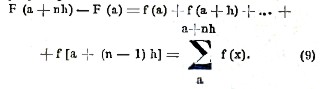
Отсюда и самая операция отыскания F(x) по данной функции f(x) называется суммированием и обозначается символом ∑, так что F(x)=∑f(x). Из самого определения символов ∑ и Δ следует, что
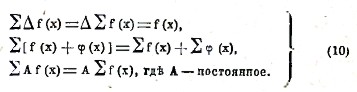
∑f(x) называется неопределенной суммой, а
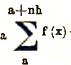
- определенной суммой от функции f(x).
Определение функции F(х) возможно только в очень ограниченных случаях. Приведем здесь несколько простейших примеров. Мы имели
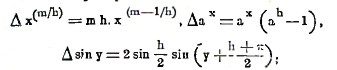
заменяя в первом из этих равенств m через m+1 и взяв в третьем равенстве вместо переменного у переменное х = у+(h+π)/2 мы получим
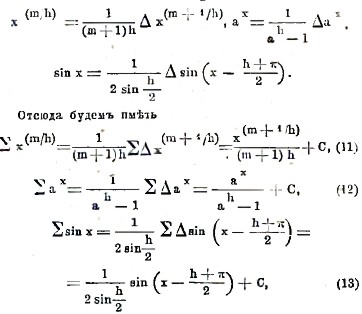
где С — произвольное постоянное.
Так как всякая целая положительная степень х разлагается по факториалам (формула 2), то формула (11) решает вопрос о суммировании всякого многочлена. Применим формулу (9) к суммированию рядов
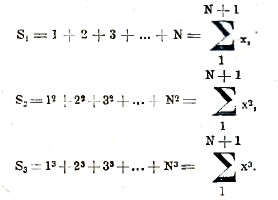
В силу равенств (3) мы имеем
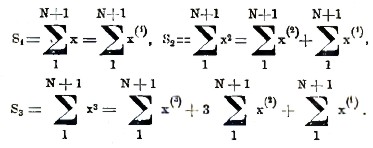
Но формула (11), где h = 1, дает
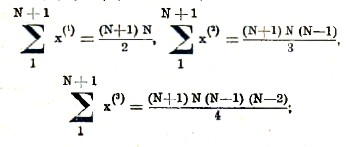
поэтому мы будем иметь

т. е. S3 = S12. Выведем теперь формулу суммирования по частям. Мы имели (формула 1)
Δ(uxvx) = vxΔux + ux + hΔvx; отсюда получаем vxΔux = Δ (uxvx) - ux + hΔvx , и
![]()
это и есть искомая формула. Так как ∑Δ(uxvx) = uxvx + С, то формула (14) сводит операцию ∑vxΔux к операции ∑ux+hΔvx, которая может быть значительно проще. Просуммируем, например, функцию xaх. Положим для простоты h = 1; тогда
∑xax = 1/(a-1) ∑xΔax, и задача приводится к вычислению ∑xΔax.
Мы видим, что в рассматриваемом случае
vx = x, ux = ax, ux+1=ax+1 Δvx = 1, и формула (14) дает
![]()
поэтому
![]()
Применим полученный результат к вычислению суммы
N
∑xax
1
мы будем иметь по формуле (9)
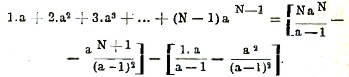
Если а<1, то при неограниченном возрастании числа N количество NaN и аN+1 стремятся к нулю, и в пределе мы получим сумму бесконечного ряда
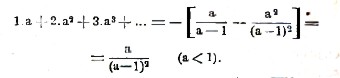
В частности, положим а = е-(ρ+√-1φ), где ρ>0. Тогда, так как
е-m(ρ+√-1φ) = e-mρ[cos mφ - √-1 sin mφ], то из предыдущей формулы мы найдем сумму ряда
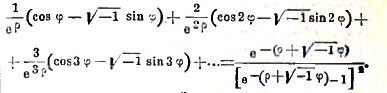
Сравнивая между собой действительные и мнимые части в обеих частях предыдущего равенства, мы будем иметь после различных упрощений

где
![]()
Определенная сумма и определенный интеграл связаны важной формулой, известной вод именем формулы Эйлера или Маклорена. Мы имели из формулы Тейлора (формула 4)

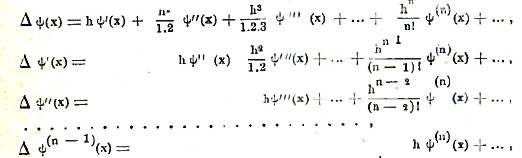
Умножая эти формулы последовательно на 1, A1h, A2h2,…, An-1hn-1… и, складывая между собой полученные результаты, мы будем иметь
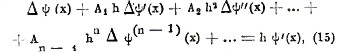
Если числа А1, А2,…, Аn-1… выбраны таким образом, чтобы они удовлетворяли уравнениям
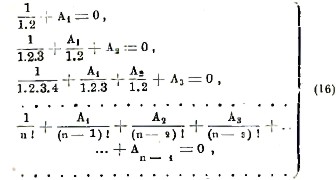
Заметим, что для краткости мы опустили остаточные члены в формулах для ΔΨ(x), ΔΨ’(x),…, а потому и формула (15) получилась без остаточного члена: его выражение можно найти в специальных сочинениях, указанных в конце статьи. Положим
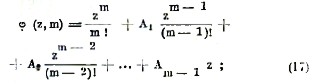
Функция φ(z1, m) называется функцией Бернулли, причем А1, А2, … определяются уравнениями (16). Очевидно, что φ(0, m) = 0, φ(1, m) = 0, и уравнения (16) можно представить в сокращенном обозначении φ(1, 2) = 0, φ(1, 3) = 0,.., φ(1, n) = 0. Нетрудно убедиться, что А1 = -1/2, что все остальные коэффициенты с нечетными указателями А3, А5, А7, … равны нулю, а коэффициенты с четными указателями А2, А4, А6, … попеременно положительны и отрицательны. Поэтому, полагая
![]()
мы можем представить уравнения (16) в виде

Числа В1, В2, В3, … называются числами Бернулли. Первые десять из этих чисел имеют следующие значения:

Все числа Бернулли положительны и неограниченно возрастают с возрастанием их указателя. Эти числа можно также определить, как коэффициенты разложения функции x/(ex-1) по степеням х при помощи формулы
![]()
В самом деле, отсюда имеем
![]()
разлагая ex по степеням, выполняя умножения и сравнивая между собой коэффициенты при одинаковых степенях х, мы придем к уже найденным уравнениям, определяющим числа Бернулли. Эти числа можно еще определить символической формулой Bp=|Csp|, где
![]()
Если условимся заменять Ck через Сk, т.е. заменять показатель указателем. Функции и числа Бернулли часто встречаются в математике, и им посвящено много работ; из русских математиков их теорией занимались Имшенецкий, Сопин, Вороной. Мы приведем здесь без доказательства еще следующие формулы

Вернемся теперь к формуле (15); заменяя в ней А1 через -1/2 и вводя вместо А2, А3 ... числа Бернулли, мы можем представить эту формулу в виде
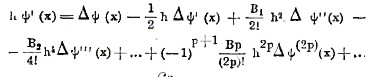
Положим
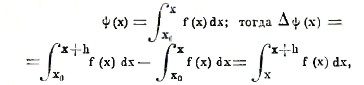
и предыдущая формула принимает вид
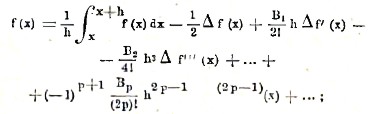
полагая в этой формуле последовательно x=a, a+h, a+2h,…, b-2h, b-h и суммируя полученные результаты, мы и придем к формуле Эйлера или Маклорена
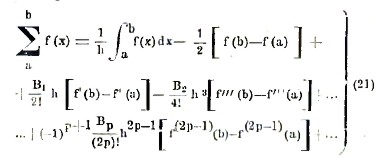
Этой формулой можно пользоваться и для вычисления суммы и для вычисления интеграла. Применим ее сначала к вычислению, например, интеграла
∫01dx/(1+x)= log 2. Здесь мы имеем а = 0, b = 1, f(х) = 1/(1+х); положим h = 1/10. Тогда

и мы получаем
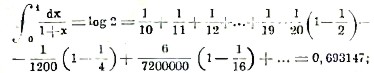
но, чтобы судить о точности полученного результата, всегда приходится обращаться к остаточному члену. Применим теперь формулу Эйлера к нахождению суммы, именно, выведем из нее формулу Стирлинга, служащую для приближенного вычисления произведения 1.2.3.4 ... (z — 1).z. Взяв логарифм от этого произведения, будем иметь выражение log (1.2.3... z) = log z +
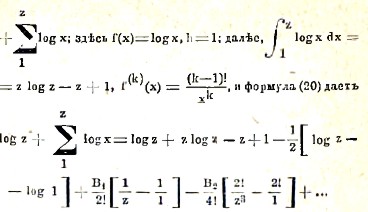
Обозначая постоянное, входящее в эту формулу, через log С, т. е. положив
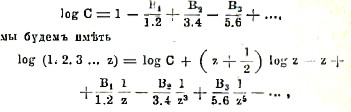
или, переходя от логарифма к числу,

Это — формула Стирлинга. Ряд φ(1/z) — расходящийся; сначала его члены убывают, а, после наименьшего члена, дальнейшие члены начинают неограниченно возрастать. Если в формуле (21) мы вычислим сумму членов этого ряда до его наименьшего члена и отбросим все остальные, то мы будем иметь тем более точное значение произведения 1.2.3...Z, чем больше число z. Постоянное С в формуле Стирлинга равно √2π. Это можно доказать, воспользовавшись формулой Валлиса
![]()
которую можно преобразовать следующим образом

Вставляя сюда из формулы Стирлинга значения произведений 1.2...n, 1.2...2n и переходя к пределу, мы и получим С = √2π.
Во многих вопросах исчисления конечных разностей удобно пользоваться производящими функциями, введенными Лапласом (Тhéorie des Probabilités). Пусть будет uх = f(х) функция от х; дадим х все целые значения от —∞ до +∞ и составим ряд
![]()
Функция ф(t) называется производящей функцией для функции uх (uх есть коэффициент при tx) и обозначается символом ф(t) = Guх. Зная Guх, не трудно найти GΔuх. В самом деле, разделив обе части равенства (23) на t, мы найдем, что коэффициентов при tx в t-1 ф(t) будет служить уже uх+1; следовательно,
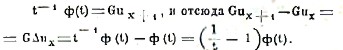
Повторяя ту же операцию любое число раз получим
![]()
Укажем на частном примере применение производящих функций. Мы получили
Guх+n = t-nφ(t); по
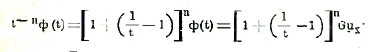
Разлагая
![]()
по формуле бинома, получим
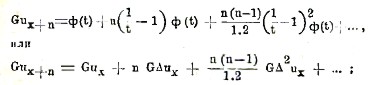
отсюда находим уже известную формулу (6)
![]()
Можно также искать
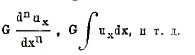
III. Перейдем теперь к уравнениям в конечных разностях. Уравнением в конечных разностях n-го порядка называется всякое уравнение вида
![]()
Так как Δux = ux+1-ux (для простоты мы положили b = 1) и Δkux = Δk-1ux+1 - Δk-1ux, то уравнение (24) можно представить также в виде
![]()
Это уравнение равносильно бесчисленному множеству уравнений
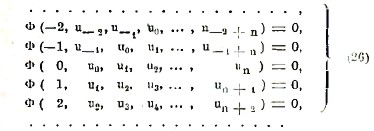
Отсюда видно, что давая, например, количествам u0, u1, u2,…, un-1 произвольные постоянные значения мы, вообще, можем определить из системы (26) все un, un+1, un+2,…, и все u-1, u-2, u-3,.. Таким образом, уравнение (26) имеет бесчисленное множество решений, каждое из которых определяется n производными постоянными u0, u1, u2,…, un-1. Решить или проинтегрировать разностное уравнение (25) это значит определить из него uх, как функцию только от х и от n произвольных постоянных. Мы здесь рассмотрим только самые простые случаи. Начнем с уравнения первого порядка
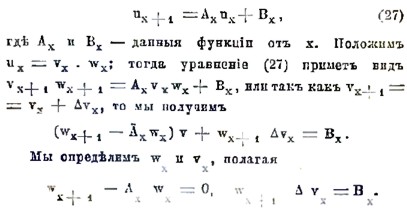
Из первого условия последовательно выводим

Определив wx+1, мы из второго условия получим
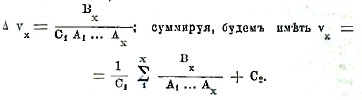
Таким образом окончательно, полагая С = С1 С2, найдем интеграл уравнения (27)
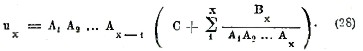
Рассмотрим, например, уравнение
ux+1 = 1/a ux + x, где а – постоянное. Здесь
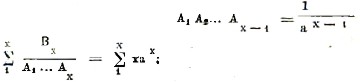
последнюю сумму мы уже умеем вычислять (по формуле 14), и, включая постоянные члены, получившиеся после суммирования, в произвольное постоянное С, мы будем иметь
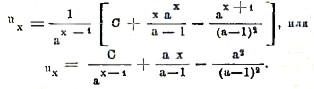
Особенно примечательны линейные уравнения с постоянными коэффициентами, т. е. уравнения вида
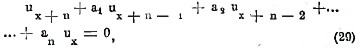
где а1, а2,.., аn — постоянные. Мы решим это уравнение, полагая ux=rx; тогда уравнение (29) обращается в
![]()
и, после сокращения на rx, мы получим алгебраическое уравнение n-ой степени
![]()
Пусть будут r1, r2,…, rn корни этого уравнения; тогда общий интеграл уравнения (29) будет
![]()
где С1, С2,...,Сn — произвольные постоянные.
Рассмотрим, например, уравнение
![]()
здесь уравнение по r будет r2-9r+20 = 0, и r1 = 5, r2 = 4; следовательно, ux = С15x+С24x. Если бы в правой части уравнения (29) стояла какая-нибудь функция f(х), то общий интеграл был бы равен какому-нибудь частному интегралу уравнения, сложенному с выражением (31). Например, проинтегрируем уравнение
![]()
Будем искать частный интеграл вида ux = Ax+B; тогда ux+1=A(x+1)+B, ux+2=A(x+2)+B.
Вставим эти значения в рассматриваемое уравнение; мы получим (12А — 1) х + 12 В — 7 А = 0, и мы удовлетворим рассматриваемому уравнению, взяв 12А—1 = 0 и 12В — 7А = 0, откуда А = 1/12, В = 7/144. Следовательно, общий интеграл данного уравнения будет
ux = x/12 + 7/144 + C15x + C24x. Можно также рассматривать системы совместных уравнений. Поясним это на следующем примере
ux+1+avx = 0, vx+1+aux = 0 (а — постоянная).
Положим ux = Mrx, vx = Nrx; тогда наши уравнения дадут Мr + Na = 0, Ма + Nr = 0. Исключая отсюда М и N, будем иметь
![]()
следовательно, r1 = а, r2 = -а. Вставляя значения r в уравнение Мr + Na = 0 мы получим или N1=-M1, или N2 = +М2, и общие решения предложенной системы будут
![]()
Можно рассматривать также уравнения дифференциально-разностные, как, например, уравнение
![]()
Попытаемся удовлетворить этому уравнению, положив uх = еmх; мы получим еmх (еm — 1 + m) = 0; следовательно, мы можем представить интеграл рассматриваемого уравнения в виде
u1 = С1em1x + С2em2x +…, где С1, С2... — произвольные постоянные, и m1, m2 — корни уравнения (еm — 1 + m) = 0. Такие смешанные уравнения встречаются, например, в анализе при разложении в ряды, в механике в теории движения сочлененных систем и т. д. Разностными уравнениями пользуются во многих вопросах математики и особенно в ее приложениях, но теория их разработана значительно менее теории дифференциальных уравнений.
IV. Задача интерполирования, не в самом ее общем виде, состоит в следующем: Даны значения f(х0), f(х1), f(xn) аналитически неизвестной функции f(х), соответствующие значениям x0, х1,…, xn аргумента; определит значение f(α), соответствующее значению х=α аргумента, заключающемуся между крайними значениями х0 и хn (х0 < α <xn). Как мы увидим из всего дальнейшего, решение этой задачи содержит много произвола.
1) Мы можем применить метод графического интерполирования. Для этого на плоскости прямоугольных осей координат отметим точки [у0 = f(х0), x0], [y1= f(x1), x1],...; соединив между собой от руки или при помощи лекал эти точки (х0, у0), (х1, у1),... непрерывной кривой, мы непосредственно на чертеже можем измерить ординату yα = f(α), соответствующую абсциссе х = α. Этот способ — самый удобный, когда не требуется большой точности (см. черт. 1).

Черт. 1
2) Метод параболического интерполирования. Подыскиваем многочлен вида f(х)=а0+а1х+а2х2+...-аnхn, коэффициенты и степень которого определятся из данных условий задачи. Если разности х1-х0, х2-x1,... различны, то можно воспользоваться формулой Лагранжа, которая дает для неизвестной функции f(х) приближенное выражение F(х)
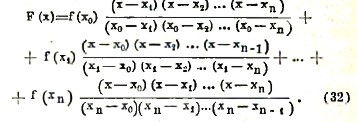
В самом деле, например, при х = х1, все дроби в формуле (32) обратятся в нуль, кроме второй, которая обратится в единицу, и мы получим F(x1) = f(х1); точно так же, при х = х0, мы будем иметь F(x0) = f(х0), при х = x2 получим F(x2) = f(х2) и т. д. Давая переменному х значение α, мы получим F(α), которое и будем считать приближенным значением количества f(α). Найдем, например, значение функции, соответствующее значению х = 3, если известно, что значениям х = 2, 4, 5 соответствуют значения функции 6, 8, 3. В этом случае х0 = 2, х1 = 4, х2 = 5, f(х0) = 6, f(x1) = 8. f(х2) = 3, α = 3, и мы имеем по формуле (32)
![]()
или, после упрощений, F (х)=(х-4)(х-5)-4(х-2)(х-5) + (х-2)(х-4). Вставляя сюда значение х = α = 3, получим приближенное значение для f(3)=F(3)= 9. Выполняя умножения в F(х), будем иметь F(х) = — 2х2 + 13х — 12. Если же все разности х1-х0=х2-x1=...=хn-хn-1 между собою равны, то можно воспользоваться также формулой Ньютона. Для этого обратимся к формуле (6). Положим в ней х=а, а+nh=х; тогда мы будем иметь n = (x-a)/h, n-p = (x-a-ph)/h, и биноминальный коэффициент Cnp примет вид Cnp =
![]()
Вставляя эти значения в формулу (6), мы и получим формулу Ньютона
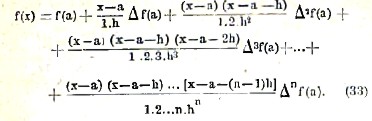
При вычислениях по этой формуле обыкновенно составляют такую таблицу (ограничимся n=4).
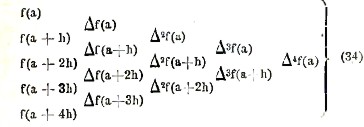
Пример. Даны: log 3,14 = 0,49693; log 3,15 = 0,49831; log 3,16 = 0,49969; log 3,17 = 0,50106. Найти приближенное значение log π = log 3,14159. В нашем случае x = 3,14159; a = 3,14; x-a = 0,00159; h = 0,01. Составляем таблицу (34):

или, удерживая только первый и второй член, log π = 0,49693 + 0,159. 0,00138 = 0,49715.
Для благонадежности результата h должно быть взято возможно меньше. Рассмотрим еще пример. Из русских таблиц смертности Борткевича имеем, что из родившихся 100 000 мужчин в возрасте 20 лет умирает 344, в возрасте 25 умирает 383, в возрасте 30 – также 383, в возрасте 35 умирает 429 и в возрасте 40 лет уже 515. Составляем таблицу (34)

Определим число умерших в возрасте 32 лет. Здесь h=5, a=20, x=32, x-a=12. Из формулы Ньютона имеем:

непосредственно же из таблиц Борткевича находим 397. Если бы h было меньше, то и разница была бы меньше. Если мы хотим, чтобы степень многочлена a0 + a1x +…+ anxn была на несколько единиц меньше числа данных значений функции, то мы можем определить коэффициенты по способу наименьших квадратов, излагаемому в теории вероятностей. Обозначим данное значение функции, соответствующее значению xi, через yi (i=0, 1, 2,.., n) и предположим, что требуется удержать только три первых члена a0 + a1x + a2x2. Мы получим достаточное число уравнений для определения a0, a1, a2, если выразим, что сумма квадратов уклонений
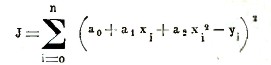
должна быть наименьшей, т. е. должно быть
![]()
Обозначая для простоты средние значения
![]()
Через [x], [x2], мы получим уравнения для a0, a1, a2

Чебышев дал другой способ параболического интерполирования. Существуют методы интерполирования и при помощи периодических функций.

Черт. 2
Из чертежа 2 видно, как должно осторожно относиться к результату интерполирования, если характер искомой функции совершенно неизвестен, особенно если число данных значений невелико. Так, интерполируя по трем данным f(x0), f(x1), f(x2) мы получим интерполяционную кривую А1А2А3 тогда как действительная кривая может иметь вид М0А1М1А2М2А3; мы видим, что уклонения очень невелики. Интерполирование применяется во многих задачах статистики, при вычислениях определенных интегралов (см. квадратура) и др.
Литература: Марков, «Исчисление конечных разностей» (1911); Тихомандрицкий, «Курс теории конечных разностей» (1890); Ващенко-Захарченко, «Лекции разностного исчисления»; Чеваро, «Элементарный учебник алгебраического анализа» (т.I, 1913); Чебышев «Сочинения».
А. Некрасов.
| Номер тома | 22 |
| Номер (-а) страницы | 332 |
