Излучение

Излучение. Излучением называется процесс передачи энергии материальными телами эфиру — той среде, которая заполняет собой все пространство и которая является носителем всех вообще электромагнитных явлений и, в частности, явлений света и лучистого тепла. Переданная телами через излучение в эфир энергия движется в нем в виде волн, распространяющихся со скоростью 300 000 километров в секунду. Вся энергия, доставляемая земному шару солнцем, — результат грандиозного процесса излучения, происходящего на солнце. Теория процессов излучения, т. е. процессов возникновения света — видимых или невидимых глазу волн, непосредственно примыкает к теории света изучающей условия распространения световых волн уже возникших.

Процессы излучения распадаются на несколько групп: а) «температурное излучение», — то излучение, которое появляется при повышении температуры твердого или жидкого тела; разлагая свет от такого источника при помощи призмы или решетки, мы получаем непрерывный спектр, т. е. непрерывную последовательность волн различной длины. От этого надо отличать b) свечение газа, например, раскаленного пара в пламени газовой горелки или светящийся газ под действием электрического разряда (см. разряд электричества в газах). Излучение  этого типа дает прерывный спектр, состоящий из линий или полос (Linien-spectrum, Banden-spectrum), и, наконец, с) весьма разнообразный и сравнительно мало изученный класс явлений т. н. люминесценции, т. е. свечения, вызываемого целым рядом причин — освещением (флуоресценция и фосфоресценция); механическими причинами (трибо-люминесценция), например, свечение разламываемого куска сахара; химическими процессами (хеми-люминесценция) и т. д. а) В двух последних случаях излучение представляет собой процесс более сложный, чем простое температурное излучение. Законы температурного излучения изучены в настоящее время наиболее детально. Всякое твердое или жидкое тело, нагретое до температуры в 500°С, начинает испускать свет, интенсивность света быстро возрастает с температурой; при этом меняется и характер испускания (например, красное и белое каление), т. е. распределение энергии между волнами, составляющими спектр данного тела, изменяется от температуры. Кроме того, степень и характер испускания зависит от природы светящегося тела. Существует, однако, один тип температурного излучения, при котором индивидуальные особенности излучающего тела совершенно не сказываются — это т. н. излучение абсолютно черного тела. Представим себе нагретое до какой-нибудь температуры t° тело А, заключающее в себе замкнутую полость, внутри которой находится какое-нибудь тело В; положим, что из этой полости выкачен воздух; тогда тепло от оболочки А будет передаваться телу В только излучением. Через некоторое время тело В нагреется до температуры оболочки. Если мы будем поддерживать температуру оболочки А, то температура В меняться не будет; наступит состояние подвижного равновесия: тело В будет получать от оболочки в единицу времени столько энергии, сколько оно испускает обратно к А. Если тело поглощает долю α_b и само испускает в единицу времени Е_b , то подвижное равновесие будет определяться равенством

Е_b = α_bе_а (1)

Так как процессы испускания и поглощения происходят в самом теле независимо от окружающих предметов, то тело В всегда будет при температуре t испускать и поглощать одинаково; так, например, если оно будет помещено в другую полость A₁ тела из другого вещества, но при той же температуре t, то оно, рано или поздно нагревшись до той же температуры t, будет испускать Е_b и поглощать долю α_b падающей на нее от оболочки A₁ энергии е_а1, по-прежнему мы будем иметь

Е_b = α_bе_а1 (2)

Сравнивая (1) и (2), получаем е_а = е_а1, т. е. два различных тела испускают в находящуюся внутри них полость при одной и той же температуре одинаково независимо от их способности испускать и поглощать; необходимо, однако, иметь ввиду, что тела, составляющие оболочку, должны быть абсолютно непрозрачны, чтобы не выпускать из полости лучистой энергии и не впускать ее извне. Такое излучение, существующее внутри замкнутой полости с непрозрачной оболочкой, поддерживаемой при постоянной температуре, носит название излучения абсолютно черного тела. Почему оно так называется, нетрудно выяснить. Если мы предположим, что тело В абсолютно черное, т. е. что оно поглощает всю падающую энергию, то α_b = 1 (α_b, вообще говоря, правильная дробь, показывающая, какая доля падающей энергии поглощается). Тогда на основании (1) или (2) Е_b = е_а, т. е. такое абсолютно черное тело так же испускает, как наша оболочка. Равенство (1) можно написать так:

Е_b/α_b = е_а (3)

что верно для любого тела В:

Е_b/α_b = Е_b1/α_b1 = Е_b2/α_b2 = е_а (3¹)

Откуда следует, что если тело В испускает сильнее тела В₁; то во столько же раз оно должно сильнее поглощать, так как при одной и той же температуре оба отношения Е_b/α_b и Е_b1/α_b1 равняются одной и той же величине е_а.

Кирхгофу (1859) удалось показать, что сказанное верно не только для всего излучения, но и для любой длины волны λ, выделенной из сплошного спектра:

Е_bλ /α_bλ = е_аλ (4)

Доказательство Кирхгофа и другие позже предложенные доказательства его закона (4) были подвергнуты строгой критике, и лишь в самое недавнее время (1912) Гильберту удалось дать безупречное с логической стороны доказательство этого закона. Таким образом, излучение черного тела не зависит от индивидуальных свойств этого тела, и, следовательно, задача сводится к выяснению распределения энергии в спектре и зависимости, как этого распределения, так и полного излучения от температуры, не принимая в расчет свойств вещества оболочки.

Вся теория «черного излучения», как часто сокращенно обозначают излучение абсолютно черного тела, основана на изучении указанного выше излучения внутри замкнутой полости. Из сказанного ясно, что в пространстве между оболочкой и телом В находится лучистая энергия, раз существует поток ее от А к В и наоборот. Следовательно, мы можем говорить о количестве энергии, заключенной в каждом кубическом сантиметре пространства, отделяющего А от В, или о плотности лучистой энергии, причем эта плотность будет тем больше, чем интенсивнее будут потоки энергии от А к В и наоборот, что в свою очередь обусловливается температурой. Отсюда мы можем говорить о «плотности» лучистой энергии (при установившемся подвижном равновесии), находящейся в равновесии с телом температуры Т, и приписывать этому излучению температуру Т того тела, с которым эта лучистая энергия находится в равновесии. Так как вещество оболочки (см. выше) не играет роли, то мы можем этой оболочке в наших рассуждениях приписывать какие угодно свойства и какую угодно форму: можем, например, представить ее себе в виде цилиндра с поршнем, а стенки или поверхности поршня наделять какими угодно свойствами; например, мы можем предполагать, что поверхность поршня представляет собой идеальное зеркало, т. е. отражает всю энергию, какая на нее падает; раз она ничего не поглощает, то она и ничего не испускает. Если тело В помещено в оболочку А с идеально отражающей внутренней поверхностью, то по-прежнему Е_b = α_bе_а. только е_а будет означать не испускаемую зеркальной поверхностью энергию, так как вполне отражающее, т. е. не поглощающее тело, и не излучает, а лучистую энергию, вышедшую из В и отраженную от А. Рано или поздно установится подвижное равновесие, когда тело В будет посылать в секунду столько энергии, сколько ее поглотится из отраженного от зеркальной стенки потока, а так как Е_b и α_b то же самое, то и е_а должно быть одинаково с прежним.

Представим себе цилиндр с поршнем; пусть внутренняя боковая поверхность этого цилиндра выложена идеальным зеркалом, а также и обращенная внутрь поверхность поршня; положим далее, что дно цилиндра пропускает свободно лучистую энергию и может быть приведено в соприкосновение с излучающим телом А какой угодно температуры Т. Тогда ясно, что в пространстве под поршнем будет находиться лучистая энергия, соответствующая черному излучению температуры того тела, к которому прикасается дно цилиндра. Медленно поднимая поршень и дожидаясь установившегося состояния, мы получим большой объем, занятый лучистой энергией той же плотности и соответствующей той же температуре тела Т. Закрыв дно цилиндра заслонкой, не пропускающей лучистой энергии, и опуская поршень, мы можем как угодно увеличить плотность запертой там энергии и довести, таким образом, ее до плотности, соответствующей более интенсивному обмену лучистой энергии телами более высокой температуры. Приводя теперь дно цилиндра в соприкосновение с телом более высокой температуры Т₁; вынимая заслонку и опуская поршень еще дальше, мы можем перевести лучистую энергию, взятую у тела А с температурой Т, телу В с более высокой температурой Т₁. Термодинамика (см.), или механическая теория тепла, показывает, что нагреть тело высокой температуры за счет тела низкой можно, только затратив известное количество работы, — это вытекает из второго основного закона термодинамики.

Отсюда два исхода: или мы должны признать, что второй закон термодинамики неприложим к явлениям излучения или что в изложенном воображаемом опыте мы при опускании поршня и при сдавливании лучистой энергии под поршнем совершаем работу, т. е. лучистая энергия — волны эфира — оказывали давление на поршень.

Рассуждая таким путем, Бартоли показал, что для того, чтобы согласить процессы излучение со вторым законом термодинамики, необходимо допустить существование давления волн, несущих лучистую энергию, причем численно это давление, рассчитанное на кв. см  поршня, должно равняться плотности энергии, падающей на поршень. Так как в пространстве под поршнем волны двигаются по всем направлениям, то при подсчете давления необходимо принять в расчет только ту часть ее, которая соответствует волнам, падающим на поршень, как показывают вычисления этой величины, 1/3  всей плотности энергии.

Весьма любопытно, что давление волн, переносящих лучистую энергию, которое необходимо допустить, чтобы согласить явление излучение со вторым принципом термодинамики, как раз совпадает с тем, что было выведено независимым путем основателем электромагнитной теории, Максвеллом. Классические опыты П. Н. Лебедева фактически подтвердили предположения Максвелла-Бартоли. Если мы примем существование давления на поршень и приложим к указанной системе — излучающее тело + цилиндр с лучистой энергией — оба закона термодинамики, то можно показать, как это сделал впервые Больцман, что плотность энергии «черного излучения», соответствующего абсолютной температуре Т, пропорциональна четвертой степени этой температуры, т. е.

U = аТ⁴ (4)

Этот результат был найден еще раньше эмпирически Стефаном и получил теперь название закона Стефана-Больцмана. В настоящее время закон этот весьма тщательно проверен на опытах с искусственным черным телом. Для этого делают в закрытом со всех сторон ящике, который поддерживается при определенной температуре, небольшое отверстие, из которого выпускают, следовательно, «черное излучение» полости, количество выходящей энергии в единицу времени, пропорционально плотности (4).

Закон Стефана-Больцмана, однако, не решает еще вопроса — в нем речь идет о полном излучении, и мы из него не можем извлечь решительно ничего относительно распределения энергии между волнами различной длины. Дальнейший шаг был сделан В. Вином. Если в цилиндре с зеркальными стенками сдавливать поршнем находящуюся там лучистую энергию, соответствующую определенной температуре, если, например, начать опускать поршень, то, благодаря уменьшению объема и сообщению извне энергии, увеличивается плотность энергии, но при отражении от движущегося зеркала изменяется и длина волны.

Чтобы выяснить изменение длины волны при отражении от движущегося зеркала, рассмотрим следующий простой процесс.

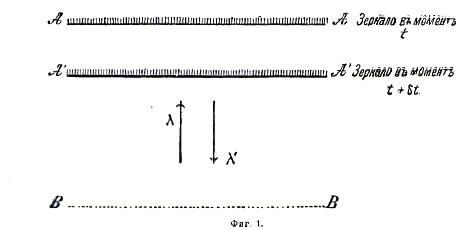
Волны λ, идущие к зеркалу, пусть после отражения имеют длину λ₁. В момент t зеркало занимает положение А, и на пространстве АВ находится АВ/λ волн λ и АВ/λ₁ волн λ₁ – всего АВ(1/λ + 1/λ₁). В позднейший момент t + δt в пространстве между A₁B волн будет меньше, именно А₁В(1/λ + 1/λ₁) составляется тем, что волны λ₁ за промежуток времени δt уходят в большем числе v₁δt, чем волны λ, поступающие в числе vδt в пространство между зеркалом и В. Итак (АВ – А₁В)(1/λ + 1/λ₁) = (v₁ – v)δt (4); а так как АВ – А₁В = АА₁ = Vδt пространству, проходимому зеркалом за время δt со скоростью V, то из (4) получаем (1/λ + 1/λ₁)v = v – v₁ (3), где v₁ и v числа волн, проходящих в секунду; так как все эти волны должны уложиться на с = 300 000 км пространстве, проходимом светом в течение секунды, то для длины волн λ и λ₁  получаем λ = с/v, λ₁ = с/v₁, а внося эти выражения в (5) и решая относительно v₁, получаем

V₁ = (c+V)/(c-V)v (6).

Это выражение и показывает, насколько изменяется частота колебаний при отражении от движущегося зеркала. Следовательно, на основании этой связи между изменением длины волны при отражении и скоростью движения зеркала и на основании выражения работы против силы давления можно, как показал Вин, вывести связь между плотностью энергии соответствующей определенной частоте v₁, частотой v и абсолютной температурой Т; получается выражение (скорость зеркала при этом расчете исключается — она входит и в выражение работы, и в выражение изменения частоты при отражении)

U_v = v³F(T/v) (7),

где F знак функции, относительно формы которой из рассуждения Вина ничего нельзя сказать. Таким образом, закон Вина только до известной степени ограничивает выбор функций, могущих изображать закон распределения энергии в спектре. Но уже и в такой форме из (7) можно извлечь весьма многое; найдя при данной температуре Т область спектра v_m, соответствующую максимуму излучения, мы можем составить выражение T/v_m = b (7), показываем, что максимум всегда будет при одном и том же значении b, так что определив раз навсегда b = T/v_m,  мы для любой температуры Т можем найти v_m, т. е. положение максимума энергии в спектре. Опыт вполне подтверждает это следствие теории. Закон Вина показывает, что может дать термодинамика для теории излучения. Дальше идти этим путем нельзя, мы должны глубже заглянуть в самый процесс излучения, составить себе определенную картину процесса — определенную модель и, отправляясь от нее, определить вид функции F в (7). Попыток в этом направлении было сделано несколько, но верной и полной картины изучаемых явлений все они, за исключением теории Планка, не дают. В своих исследованиях Планк отправляется от основных положений электромагнитной теории (см. свет), принимающей волны эфира любой длины, а, следовательно, и световые за волны электромагнитные, которые, следовательно, могут возникнуть только благодаря колебаниям электрических зарядов, находящихся в любом атоме.

Если мы себе представим ряд колеблющихся зарядов вибраторов или резонаторов, имеющих определенный период, заключенный в замкнутую зеркальную оболочку, то с течением времени установится подвижное равновесие. Различие с указанными выше случаями будет только в том, что волны будут соответствовать определенному периоду колебания резонатора; внутри полости получается «черное излучение», соответствующее определенной длине волны λ — определенному тону резонатора. Пользуясь законом электродинамики, Планк вывел связь между плотностью энергии U_λ, соответствующую черному излучению при этих условиях, и средней энергией резонатора Е. Получается простое соотношение

U_λ = 8π/λ⁴Е (7)

Если предположить, что резонаторы находятся в температурном равновесии с материей, их заключающей, то можно показать, что энергия резонатора Е в среднем должна равняться 1/3 энергии поступательного движения молекул при данной температуре, т. е.

E = ½ (RT/N)T  (8).

где R газовая постоянная, рассчитанная для граммолекулы газа, а N число молекул в граммолекуле. Вставляя (8) в (7), получаем

U_λ = 4π/λ⁴(RT/N) (9)

Если бы у нас было большое число резонаторов всевозможных периодов, находящихся друг с другом в температурном равновесии, то для всех них Е будет одинаково, т. е., следовательно, (9) представляет собой закон распределения энергии в спектре. Выражение (9) было выведено лордом Рэлеем и приложимо только к инфракрасной области спектра (т. е. для длинных волн, как на это указывал и сам Рэлей), где, однако, оно выражает ход явлений вполне удовлетворительно. Более того, определив количество излучаемой черным телом энергии для определенной длины волны λ, можно, зная величину газовой постоянной, определить N, т. е. число молекул в граммолекуле какого угодно вещества; измерения дали число N = 64∙10²², что находится в весьма удовлетворительном согласии с числами, получаемыми совершенно иными путями и лежащими в пределах от 60∙10²² до 75∙10²².

Как бы то ни было, указанная теория неприложима к коротким волнам — мы получаем непрерывное и быстрое возрастание энергии по мере уменьшения длины волны λ, тогда как в действительности существует максимум, за которым по мере уменьшения λ следует быстрое падение энергии. Это противоречие было устранено совершенно новой гипотезой Планка, введение которой в науку в 1901 г., без сомнения, составляет новую эпоху в развитии современной физики: всякий резонатор, испускающий волны, частота которых измеряется числом v, может испускать лучистую энергию не сплошным и непрерывным потоком, а лишь отдельными, вполне определенными порциями — «квантами» — или небольшими их кратными, причем величина такой порции пропорциональна частоте: hv, где h универсальная постоянная, и что, следовательно, те резонаторы, какие в любой данный момент испускают лучистую энергию, должны обладать энергией, кратной hv. Отсюда при определении средней энергии резонатора Е, находящегося в температурном равновесии с газом температуры Т, надо еще принять в расчет, что каждый резонатор не может иметь любой энергии, и для того, чтобы данный резонатор, дающий волны, лежащие в фиолетовой части спектра, мог излучать, он должен получить одну или несколько «больших порций» hv, так как v возрастает к фиолетовому концу спектра; следовательно, получение коротких волн требует особых условий большого предварительного поглощения энергии, а потому далеко не все резонаторы, соответствующие коротким волнам, будут излучать. Этим и объясняется падение энергии в спектре к фиолетовому концу. Точный подсчет, сделанный Планком, дает для средней энергии резонатора

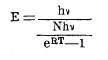
или, переходя от частоты v к длине волны λ:

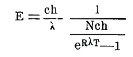
где l основание неперовых логарифмов, а для плотности энергии получаем:

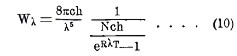
Если мы закон Вина (7) выразим в длинах λ волн, вместо частоты v, то получим

W_λ = (1/λ⁶)F₁(λT).

Таким образом, закон Планка (10) дает выражение той функции F, которая при выводе закона Вина оставалась неопределенной. Формула Планка была неоднократно подвергнута опытной поверке, и совпадение, получающееся между теорией и опытом, оказывается вполне удовлетворительным.

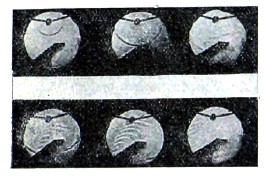
Теория Планка дает, таким образом, вполне определенный ответ на вопрос, какое распределение энергии должно быть у абсолютно черного излучающего тела, и опыты показывают, что именно такое распределение энергии и наблюдается. Но эта теория ничего не говорит о том, как возникают в теле колебания, образующие непрерывный спектр. Ведь, раз спектр непрерывный, то должно существовать, казалось бы, бесконечное число различных типов резонаторов, образующих непрерывный ряд v или, выражаясь терминологией акустики, мы должны иметь бесконечное число струн, дающих непрерывный переход от одного тона к другому. Оказывается, однако, что нет необходимости представлять себе такую сложную картину. Излучение  в твердом накаленном теле получается, когда заряженные электричеством частицы, составляющие атом, испытывают быстрые изменения скорости; такие быстрые изменения скорости происходят при столкновениях атомов, находящихся в непрерывных движениях или отщепившихся от них электронов. Интенсивность этих движений возрастает с температурой; при каждом толчке выделяется электромагнитная энергия, распространяющаяся в эфире со скоростью света, но не представляющая собой регулярные волны. То, что мы получаем от светящегося тела, есть сумма таких отдельных иррегулярных электромагнитных возмущений — импульсов. Из этого комплекса наши инструменты, дающие спектр, — призмы или решетки,  — улавливают отдельные периодические составляющие, они разлагают этот комплекс на правильную последовательность волн. Всего яснее можно представить себе этот процесс, происходящий в решетке, взглянув на следующий чертеж (фиг. 2), изображающий моментальные снимки в разные стадии отражения от ступенчатой фигуры — решетки уединенной волны — импульса. Мы здесь ясно видим такое преобразование отдельного импульса в правильную последовательность волн. То, что производится решеткой или призмой, можно изображать на бумаге математически, пользуясь так называемой теоремой Фурье. Исходя из подобных соображений, Лоренц и Томсон вывели законы распределения энергии в спектре, причем Лоренц ограничился задачей вывести закон распределения энергии для длинных волн. Он вывел закон Рэлея, а Томсон показал, что, сделав некоторые предположения относительно процессов, происходящих при столкновении двух заряженных тел (предположения, потому что точное решение этой задачи представляет колоссальные математические трудности), можно получить согласное с опытом распределение энергии в спектре – закон Планка, а также при несколько иных предположениях весьма близкие к нему, но отличные результаты.

b) Излучение, даваемое газами, значительно отличается от излучения, даваемого твердыми и жидкими раскаленными телами. Так, опыты Пашена показывают, что излучение паров натрия больше, чем излучение, соответствующее черному телу для части спектра, занимаемой линиями натрия той же температуры. Таким образом, это излучение не может быть объяснено одной температурой. Здесь, следовательно, не чисто температурное излучение, а быть может, важную роль играют химические процессы. Кроме того, резкое отличие от указанного в а) типа излучения заключается в прерывности спектра. После большого числа тщетных попыток найти какую-нибудь закономерность в спектральных линиях  для различных веществ, удалось, наконец, найти для некоторых тел простые формулы, определяющие распределение линий в спектре. Так, Бальмер (1885) показал, что числа колебаний (частоты), соответствующие спектральным линиям водорода, пропорциональны 1-4/m², где m целые числа 3, 4, 5 ... 15.

Далее, благодаря исследованиям Ридберга, Кайзера, Рунге и Ритца, удалось установить подобные открытым Бальмером «серии» линий для различных веществ. Но эти формулы, за исключением отчасти формул Ритца, представляют собой чисто эмпирические формулы.

В самое последнее время, благодаря попыткам Томсона и Рутерфорда — построить модели атома, удалось найти такие (наподобие планетной системы), в которых заряженные части атома — отрицательно-заряженные электроны и центральные положительно заряженные ядра могут совершать такие колебания, числа которых образуют ряды, совпадающие с исследованными рядами линий. Прежде всего здесь необходимо отметить попытки Гарбассо и Никольсона.

Литература: Д. Филипс, «Излучение (Radiation)» (русский перевод, изд. Печатник, 1913); Р. Drude, «Lehrbuch der Optik» (1912); М. Planck, «Theorie der Wärmestrahlung» (1912); R. Wood, «Physical optics» (1911); «Новыя идеи в физике», № 4: Природа света; статья И. И. Соколова: «Природа белого света», Л. Тимирязев, «Электромагнитная теория теплового излучения» («Журнал Русского Физ.-Хим. Общества», 1909); А. Garbasso, «Theoretische Spectroscopie» (1906);  Н. Konen, «Das Leuchten der Gase und Dämpfe» (1913).

А. Тимирязев.