Колебательное движение

Колебательное движение. Всякое движение точки, неопределенное число раз повторяющееся, причем каждый раз время (Т) движения одинаково, называется периодическим движением. Если мы в какой-либо момент времени определим положение точки, величину и направление ее движения, то окажется, что спустя время Т она находится на том же месте и обладает такой же по величине и по направлению скоростью. Периодические движения могут быть бесконечно разнообразны; простейшее по характеру периодическое движение есть равномерное движение по окружности. Из всех периодических движений представляется, однако, наиболее важным гармоническое колебательное движение, ибо всякое периодическое движение может быть получено, как результат сложения большего или меньшего числа (иногда бесконечно многих) гармонических колебательных движений.

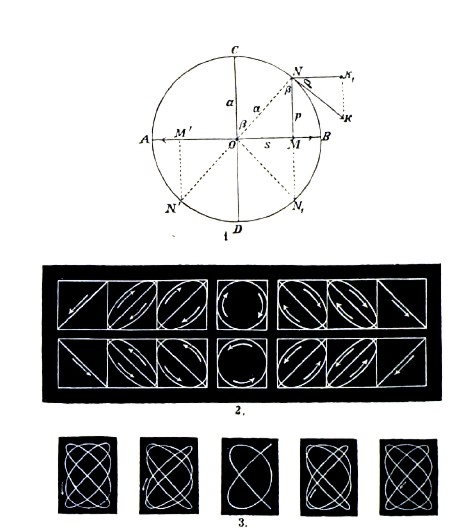
Положим, что некоторая точка N (рис. 1) равномерно движется по окружности AСBD, радиус которой а. Движение, которое в этом случае совершает  проекция М точки N на произвольный диаметр АВ, и есть гармоническое колебательное движение. Это движение совершается между крайними точками А и В, полурасстояние которых, равное радиусу окружности, называется амплитудой колебательного движения. Время Т, в течение которого точка N проходит всю окружность, а точка М совершает одно полное колебание взад и вперед, — называется периодом колебания или просто временем колебания. Угол CON называется фазой колеблющейся точки М, причем предполагается, что точка N движется по направлению от С к В, а точка М от О к В. Если точка М, занимая то же самое положение, движется по направлению от В к О, то точка N находится в N₁, и фаза равна углу CON₁. Точки М и М' находятся в противоположных фазах, т. е, их фазы отличаются на 180° или на π. Соответствующие им точки N и N' расположены на концах диаметра. Расстояние s = ОМ движущейся точки от среднего положения О, или так называемый пройденный путь выражается формулой

s = a sin2πt/T, если время t считать от момента, когда точка М находилась в среднем положении О. В общем случае пройденный путь s выражается формулой:

s = a sin(2πt/T + β₀), в которой β₀ так называемая начальная фаза, соответствующая тому моменту, от которого мы считаем время t. Скорость v точки М, совершающей гармоническое колебательное движение, пропорциональна длине перпендикуляра р = NM. Ускорение w в движении точки М выражается формулой

w = -(4π²a/T²)s, т. е. оно пропорционально расстоянию s точки М от среднего положения О и всегда направлено к точке О. Так как действующая сила пропорциональна ускорению, то отсюда следует, что материальная точка совершает гармоническое колебательное движение около некоторого среднего положения О, если она находится под влиянием силы, постоянно направленной к точке О и по величине прямо пропорциональной расстоянию точки от О. Средняя кинетическая и средняя потенциальная энергии при гармоническом колебательном движении равны между собой; они пропорциональны квадрату амплитуды. К гармоническим колебательным движениям принадлежат в простейших случаях колебания тел, вызванные упругими силами (струны, стержни, пластинки, частицы воздуха и т. д., см. звук). Сюда же относятся колебания маятника, магнитной стрелки и т. д. при весьма малых размахах. Два гармонических колебательных движения, одинаково направленных, обладающих одинаковым периодом, но различными амплитудами а и b и различными фазами β₁ и β₂, складываются в одно гармоническое колебательное движение, амплитуда А которого определяется формулой А2 = а₂+b₂+2abcos(β₁-β₂). Если разность фаз двух складываемых колебаний равна нулю (или четному числу π), то А = а + b. Если складываемые колебания находятся в противоположных фазах, т. е. разность фаз равна π (или нечетному числу π), то А = а — b; если при этом еще амплитуды а и b равны между собой, то получается А = О. Если разность фаз равна нечетному числу π/2, то

А² = а² + b². В этом случае энергия получающегося колебания равна сумме энергий слагаемых колебаний. При сложении произвольного числа одинаково направленных гармонических колебательных движений также получается гармоническое колебательное движение, амплитуда которого выражается сложной формулой. Два взаимно перпендикулярных гармонических колебательных движения, имеющих одинаковый период Т, складываются в одно движение по эллипсу. Эллипс превращается в прямую линию, и движение в гармоническое колебание, когда разность фаз складываемых колебаний равна 0 или π. Когда разность фаз равна π/2 или 3π/2, и, кроме того, амплитуды складываемых колебаний равны между собой, то в результате получается равномерное движение по окружности. Различные случаи показаны на рис. 2.

 Направление движения точек по эллипсу может быть двоякое: по или обратно часовой стрелке; направление движения зависит от разности фаз. При сложении двух гармонических колебательных движений, имеющих различные периоды Т и Т₁ и направленных одинаково, получаются сложные колебательных движения. При сложении двух взаимно перпендикулярных гармонических колебательных движений с различными периодами Т и Т₁, получаются движения, которые искусственно были воспроизведены Лиссажу. Он направил луч света на зеркальце звучащего камертона; после отражения луч падает на зеркальце второго камертона и после вторичного отражения на белую стенку, образуя на ней светлое пятно. Когда плоскости колебаний обоих камертонов взаимно перпендикулярны, то пятно, двигаясь весьма быстро, вычерчивает одну из фигур Лиссажу. На рис. 3 показаны некоторые из этих фигур для случая, когда времена колебаний Т и Т₁ относятся, как 3:4. Первый рисунок слева соответствует случаю, когда разность фаз двух колебаний равна нулю, остальные четыре — случаям, когда эта разность равна, π/12, π/6, 3π/2 и π/3. Когда материальная точка М находится под влиянием двух сил, из которых одна постоянно направлена к некоторой точке О и пропорциональна расстоянию точки М от О, а другая пропорциональна скорости v точки М и имеет направление, противоположное направлению движения точки М, то эта «последняя совершает так называемое затухающее колебательное движение, при котором последовательные полуразмахи или амплитуды составляют убывающую геометрическую прогрессию. Натуральный логарифм отношения двух последовательных размахов называется логарифмическим декрементом затухающего колебательного движения. Таковы движения тела, колеблющегося в сопротивляющейся среде, например, колебания маятника в воздухе или колебания магнита под влиянием успокоителя и т. д. Вещество, заполняющее часть пространства и обладающее по всем направлениям одинаковыми свойствами, называется изотропной средой. Допустим, что она состоит из отдельных частиц, и что одна из них начинает совершать гармоническое колебательное движение с амплитудой а и с периодом Т. Допустим далее, что частицы среды действуют друг на друга так, что движение одной из них вызывает движение соседних. В этом случае состояние движения, как бы передаваясь от точки к точке, распространяется через среду. Частицы, лежащие вдоль некоторой прямой, последовательно начинающие совершать гармонические колебательные движения, представляют то, что условно может быть названо лучом. Более точное определение термина луч вытекает из принципа Гюйгенса. Расстояние, на которое передается состояние движения в единицу времени, называется скоростью распространения колебания, или скоростью луча. Термины сохраняются и в том случае, когда распространяющееся движение не есть гармоническое колебательное движение. Частицы, расположенные вдоль луча, начинают свои движения в различные моменты времени, а потому вообще находятся при неодинаковых фазах. Длиной волны λ называется расстояние двух ближайших точек луча, находящихся при одинаковых фазах; это то расстояние, на которое колебательное движение распространяется во время одного периода Т. Длина волны λ, скорость v и период Т связаны равенством λ = vТ. Если считать время t от момента начала колебательного движения некоторой точки А, то удаление другой частицы М от ее положения равновесия во время t определяется формулой у = a sin2π(t/T-x/λ), в которой х расстояние точек М и А друг от друга, λ длина волны. Это равенство называется уравнением луча. Колебания, распространяющиеся вдоль луча, могут быть поперечные и продольные. В первом случае направление колебаний перпендикулярно к лучу; во втором случае они происходят вдоль луча. При продольных колебаниях мы имеем вдоль луча попеременные сгущения и разрежения в среде, причем в каждом данном месте попеременно происходит сгущение и разрежение. Два луча, вышедшие из одной точки Р и по различным путям дошедшие до одной и той же точки Q, вызывают в ней  два колебания, которые складываются по правилам, выше рассмотренным. Явления, которые при этом происходят, называются явлениями интерференции лучей, а про лучи говорят, что они интерферируют. Если колебания интерферирующих лучей одинаково направлены, то они складываются в одно гармоническое колебательное движение, амплитуда А которого определяется формулой

А² = а²+b² +2аb cos 2π(δ/λ), в которой а и b амплитуды колебаний двух интерферирующих лучей, λ длина волны и δ так называемая разность хода лучей, т. е. разность расстояний точек P и Q друг от друга, считаемых вдоль того и другого луча. Два луча, интерферируя, дают наибольшую амплитуду, когда разность хода δ равна четному, наименьшую, когда она равна нечетному числу полуволн. Два луча, интерферируя, взаимно уничтожаются (А = O), когда δ равно нечетному числу полуволн, и в то же время амплитуды интерферирующих лучей равны. При интерференции встречных колебаний, распространяющихся по одной и той же прямой в противоположных направлениях, образуются стоячие волны, Такое явление происходит при интерференции луча, направленного к какой-либо отражающей поверхности нормально к последней, с лучом отраженным. В стоячих волнах все частицы одновременно проходят чрез положение равновесия и одновременно достигают крайних удалений от этих положений, если амплитуды а и b двух колебаний равны между собой. Величина амплитуды вдоль луча в общем случае меняется периодически между пределами а+b  и а-b . Места, где амплитуды наименьшие, называются узлами, места, где они наибольшие, — пучностями. Если а = b, то в узлах частицы находятся в полном покое. При продольных колебаниях мы имеем в пучностях наиболее сильные движения, в узлах наиболее сильное изменение плотности, так как частицы, находящиеся с двух сторон от одного узла, всегда находятся в противоположных фазах, а частицы, расположенные между двумя узлами, — в одинаковых фазах. Если в изотропной среде из данной точки А распространяются колебания во все стороны, то амплитуда колебаний меняется обратно пропорционально первой, энергия — обратно пропорционально второй степени расстояния от А. Геометрическое место точек, до которых распространились во все стороны колебания, исходящие из некоторой точки, называется волновой поверхностью. В изотропной среде волновая поверхность есть поверхность шара. В анизотропной среде, например, в кристаллах, не принадлежащих к правильной системе, волновая поверхность есть поверхность эллипсоида, если кристаллы одноосные; в двуосных кристаллах волновая поверхность имеет весьма сложную форму. Гюйгенс дал способ построить волновую поверхность, если известны те одинаковые или различные моменты, когда колебания доходят до точек некоторой данной поверхности S. Способ Гюйгенса заключается в следующем. Все точки поверхности S следует принять за новые центры колебаний и построить около них волновые поверхности, которые образовались от моментов, когда колебательное движение достигло этих точек, до рассматриваемого момента. Огибающая (общая касательная) поверхность ко всем этим поверхностями есть искомая волновая поверхность в рассматриваемый момент. На основании этого принципа Гюйгенса объясняются законы отражения и преломления волн (волновых поверхностей) и лучей. При отражении луч падающий, нормаль к отражающей поверхности и луч отраженный лежат в одной плоскости, и угол падения равен углу отражения. При преломлении луч падающий, нормаль к преломляющей поверхности и луч преломленный лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух середин, на границе которых происходит преломление. Эта величина равна отношению скоростей распространения волн в двух средах и называется коэффициентом преломления. К распространяющимся волновым движениям прилагается принцип Допплера (см. звук, XXI, 18/19 и ХVIII, 632/3). Примерами колебательных движений, распространяющихся в среде или вдоль некоторой поверхности, могут служить явления звуковые и световые, электрические лучи Герца, волновые движения на поверхности жидкости и т. д. Принцип Гюйгенса дал возможность объяснить сложные явления дифракции, двойного лучепреломления, конической рефракции и т. д.

О. Хвольсон.