Колеса

Колеса.

Колесо имеет форму кольца, соединенного с центральной частью ступицы при помощи отдельных спиц пли при помощи сплошного диска. Колеса  разделяются на 1) экипажные и служат в этом случае для замены части работы трения скольжения работой трения качения, что представляется выгодным в смысле расхода энергии, для передвижения экипажа; 2) приводные — для передачи движения от одного вала к другому; приводные колеса, в свою очередь, разделяются на фракционные и зубчатые; 3) маховые — для уравнивания хода машин. Экипажные колеса приготовляются в большинстве из дерева (бука, дуба, вяза, гикори). Внешняя часть, или обод, колеса сгибается из одного куска, после того как дерево хорошо распарено; со втулкой соединяется при помощи спиц, вдолбленных как и во втулку, так и в обод. Для прочности на обод надевается в горячем состоянии железная полоса (шипа), сваренная в виде цельного кольца. Шипа скрепляет обод, а кроме того, уменьшает его изнашивание при езде. В некоторых случаях обод приготовляется из железа и снабжается резиновой шиной для более покойной езды. Ступина вращается на оси экипажа и для меньшего изнашивания от трения снабжается металлической втулкой, которая и трется об ось. Колеса железнодорожных вагонов и паровозов насаживаются неподвижно на ось, самая ось вращается в особых опорах (буксах). Вагонные колеса приготовляются из железа, со спицами, или из чугуна, со сплошными дисками вместо спиц. В некоторых случаях, в Америке, диск, соединяющий обод со ступицей, приготовляется из сильно спрессованного картона. Паровозные колеса приготовляются из железа и стали. Чтобы уменьшить истирание колес о рельсы, на обод надевается еще дополнительный стальной обод (бандаж). О велосипедных колесах см. IX, 355/6. Приводные фрикционные колеса представляют два массивных, правильно обточенных металлических цилиндра, насаженных на валы, между которыми должна быть устроена передача. При сближении валов и нажатии фрикционных колес друг на друга между ними устанавливается сила трения, которая передает движение от одного колеса к другому. Обозначим через w и w₁ угловые скорости одного и другого вала, через r и r₁, соответствующие радиусы фрикционных колес. Так как окружные скорости обоих колес одинаковы, то будем иметь wr = w₁r₁ откуда w/w₁ = r₁/r; следовательно, угловые скорости валов и числа их оборотов n и n₁ будут обратно пропорциональны радиусам фрикционных колес. Назовем через f коэффициент трения, тогда при нажатии колеса с сплой Т получим на окружности колес силу трения fТ. Передаваемая работа будет

N = (2πr.n.fT)/(60.75) = (2πr₁.n₁.fT)/(60.75)

Следовательно, для передачи N сил нужно прижать колеса  друг к другу с силой

Т = (N.60.75)/(2πr.n.f)

Отсюда видно, что чем больше коэффициент трения, тем меньше сила нажатия, что выгодно, так как при этом, уменьшается работа трения в  опорах. Для увеличения f поверхность цилиндров иногда обтягивается кожей, но такие колеса менее прочны.

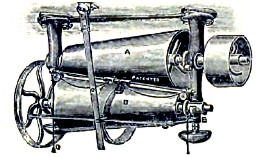
Рис.1

На фиг. 1. представлено устройство фрикционной передачи между двумя валами А и В. На валы насажены конические барабаны, между которыми проложено кожаное кольцо для увеличения коэффициента  трения. Передвигая кольцо вдоль барабанов, можно изменить отношение числа оборотов. Фракционную передачу можно устроить и между пересекающимися валами; в таком случае колеса из цилиндров обращаются в конусы.

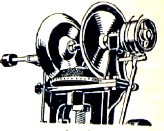
Рис.2

На фиг. 2 изображена коническая фрикционная передача в штамповальном прессе. На вертикальном валу насажен конус, составленный из кожаных дисков, плотно спрессованных (кожа имеет больший коэффициент трения); на горизонтальном валу сидят два конуса, которые могут  передвигаться вдоль вала. Прижимая тот или другой конус к кожаному конусу, можно, при постоянном направлении движения горизонтального вала, сообщать вертикальному валу движение в том или другом направлении. В фрикционных колесах возможно скольжение одного колеса по другому, а потому такая передача применяется там, где возможность такого скольжения желательна, например, при передачах с остановками; в таких случаях при включении происходит сначала скольжение, пока скорость включаемого в передачу вала не достигнет должной величины. Но ясно, что фрикционная передача совершенно не годится для тех случаев, когда необходимо точно соблюдать постоянство передаточного числа i (отношение числа оборотов одного и другого вала i = n/n₁), например, в часовом механизме.

Рис. 3

Зубчатые колеса (фиг. 3). Чтобы устранить необходимость в нажатии колеса и сообщить передаче постоянство отношений угловых скоростей, колеса снабжают зубьями. В такой передаче окружности, соответствующие соприкасающимся цилиндрам фрикционной передачи, называют начальными окружностями. Начальные окружности делят на равные части. Половина каждого такого деления будет соответствовать зубу одного колеса, а другая половина будет представлять впадину, в которую входит зуб другого колеса. Каждое такое деление на начальной окружности называется шагом колеса. Назовем через t шаг колеса, z₁ и z₂ — числа зубьев на одном и другом колесе, r₁ и r₂ — радиусы начальных окружностей, n₁ и n₂ — числа оборотов; тогда будем иметь:

t = 2πr₁/z₁ = 2πr₂/z₂, откуда z₁/z₂ = r₁/r₂ = n₂/n₁

т. е., числа зубьев прямо пропорциональны радиусам сцепляющихся колес начальных окружностей и обратно пропорциональны числам оборотов.

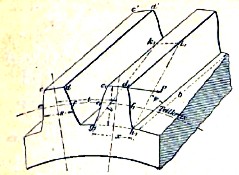
Рис. 4

Зубчатые колеса приготовляются в большинстве из чугуна, а кроне того из стали, бронзы к кожи. Каждый зубец представляет (фиг. 4) цилиндрическую поверхность, направляющая которой есть кривая, называемая профилем зуба, а образующая есть прямая сс', параллельная оси колеса. Очертание зуба симметрично относительно радиуса колеса, так как колесо должно вращаться в ту и другую сторону. Толщиной зуба называется его измерение по начальной окружности (ef=S, см. фиг. 4). Если бы колеса приготовлялись вполне точно, то шаг был бы равен двойной толщине (t = 2S). Но обыкновенно, вследствие поточности выполнения, между зубьями получаются зазоры, так что t=2S+δ, где δ — величина зазора. Измерение зуба, параллельное оси колеса (b), называется длиной зуба. Высота зуба (I) берется обыкновенно равной 0,7t. Часть, лежащая выше начальной окружности, называется головкой зуба (ее высота = 0,3t); часть, лежащая ниже начальной окружности, называется ножкой зуба (ее высота = 0,4t).

Для определения прочных размеров зуба его рассматривают как балку, ущемленную в основании зуба и нагруженную силой Р (окружное усилие), приложенной к вершине зуба (основание зуба х принимается равным 0,5t). Тогда, на основании уравнения крепости при изгибе, будем иметь: ломающий момент M = Pl = (bx²/6)B (B – допустимое напряжение материала). Вставляя сюда принятые соотношения, получим:

P.0,7t = (b(0,51)²/6)B, или P = Δbt,

где Δ — некоторый коэффициент, зависящий от допустимого напряжения материала. Для чугунных колес при ручных передачах можно принять Δ от 0,18 до 0,21 (при условии, что размеры даны в мм  и сила в кг). Для приводных передач нужно принять во внимание изнашивание зубцов и число оборотов вала; в таких случаях можно брать колеса по формуле Δ = 0,2—0,01√n, где n число оборотов в мин.

Из выражения P = Δbt видно, что нужную прочность зуба можно получить, увеличивая или шаг t или длину зуба b. Но слишком длинных зубьев делать не следует, так как в этом случае, при перекосе, давление может сосредоточиться на конце зуба (см. фиг. 4), причем зуб сломается не в основании, а по контуру g₁h₁i₁k₁. Точно так же не следует делать зубья слишком короткими, так как при этом на единицу длины придется слишком большое давление от окружного усилия, и зубья будут слишком скоро изнашиваться. При приводных передачах длина зуба может выбираться по формуле b = 0,4 t: Δ.

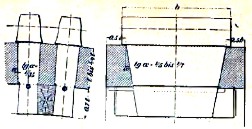
Рис.5

Иногда в чугунный обод колеса вставляются деревянные зубья (фиг. 5) для более мягкой, бесшумной передачи; в таком случае толщина деревянного зуба берется на 30% больше по сравнению с чугунным и на прибавочную толщину деревянного зуба увеличивается и величина шага.

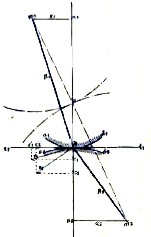
Рис. 6

Чтобы при помощи зубчатых колес движение передавалось от одного вала к другому при постоянном отношении угловых скоростей, для этого профили зубьев должны удовлетворять известным условиям. Вообразим, что на фиг. 6 m₁ и m₂ представляют оси валов, кривые a₁bd₁ и a₂bd₂ представляют части профиля зубьев, жестко связанные при посредстве стержней R₁ и R₂ с вращающимися валами. При вращении валов точка b₁, принадлежащая стержню R₁, будет двигаться со скоростью v₁, нормальной к R₁, а точка b, принадлежащая стержню R₂, будет двигаться со скоростью v₂, нормальной к R₂. Проведем линию t₁t₂, касательную к кривым a₁bd₁ и a₂bd₂ в точке b, и разложим скорости v₁ и v₂ на скорости с'₁с'₂, тангенциальные к кривым и нормальные с₁с₂. Для того, чтобы движению было возможно, необходимо, чтобы скорости с₁ и с₂, нормальные к соприкасающимся профилям зубьев, были равны, иначе зубья должны или врезаться друг в друга, или отходить один от другого. Из подобия треугольников имеем:

c₁/v₁ = ρ₁/R₁ и c₂/v₂ = ρ₂/R₂,

откуда c₁ = v₁(ρ₁/R₁) = w₁ρ₁ и c₂ = v₂(ρ₂/R₂) = w₂ρ₂,

здесь w₁  и w₂ угловые скорости одного и другого вала. Так как c₁ = c₂, то w₁ρ₁ = w₂ρ₂ или w₁/w₂ = ρ₂/ρ₁, а так как ρ₂/ρ₁ = m₂o/m₁o, то w₁/w₂ = m₂o/m₁o, а из этого следует, что для сохранения постоянства отношения угловых скоростей нормаль к кривым профилей зубьев в их точке соприкосновения должна всегда проходить через одну и ту же точку на линии, соединяющей центры вращения колес. Кривых, удовлетворяющих этому условию, может быть бесчисленное множество; профиль зуба одного колеса можно назначить произвольно, а профиль зуба другого колеса нужно будет соответственно построить. Наиболее употребительными являются следующие профили:

а) Циклические кривые. Вообразим внутри колеса А (фиг. 7) еще третью окружность С, которая имеет с окружностями А и В общую точку соприкосновения m и диаметр менее радиуса круга А. Положим, что эти три круга вращаются каждый около своего центра в направлениях, указанных стрелками, притом с такими угловыми скоростями, что окружные их скорости равны между собой. Тогда движение круга С относительно кругов А и В будет таково, как  будто бы он катился по ним, именно по наружной стороне окружности В и внутренней стороне окружности А, притом в направлении, противоположном направлению вращения этих кругов. При таком движении кругов их точки, совпадавшие в точке m, разойдутся; точка круга В перейдет в точку b, точка круга А перейдет в точку а, точка круга С перейдет в точку n, причем абсолютные пути их будут равные по длине дуги (am = bm = nm). Относительный путь точки круга С, описанный ей на плоскости вращающегося круга  В, будет эпициклоида bn, а на плоскости круга А — гипоциклоида аn. Эти 2 кривые имеют в m общую нормаль mn и, касаясь друг друга в n, нигде ниже не встречаются. Таким образом начерченная на плоскости круга А гипоциклоида an и на плоскости круга В эпициклоида bn, обе точкой m производящего круга С, при вращении кругов А и В с равными окружными скоростями будут скользить друг по другу, причем точка их касания будет перемещаться по дуге окружности С, и общая нормаль в точке касания будет проходить через мгновенный центр вращения круга С, т. о. через точку m. На этом основании эпициклоида bn может быть взята за профиль головки зуба у колеса В, а гипоциклоида an — за профиль ножки зуба у колеса А. При движении колес А и В по направлению стрелки, в случае, если ведущее колесо будет В, головка зуба колеса В начнет прикасаться к ножке зуба колеса А в точке m. Если головка зуба колеса В должна вести впадину зуба колеса А до точки n, т. е. если зубцы колес А и Б, перейдя линию центров АВ, должны сцепляться на протяжении дуги bm=am, то, соединив n с В, получаем на окружности В точку е, которая дает нам длину nе, равную высоте головки зуба у колеса В. Из этого видим, что высота зубьев ведущего колеса В тесно связана с длиной дуги bm = am = mn, которая называется дугой зацепления  после линии центров. Для того, чтобы получить профили для ножки зуба колеса В и головки зуба колеса А, нужно взять образующую окружность D внутри круга В, с диаметром не более радиуса В. Эта окружность дает нам гипоциклоиду do для ножки зуба и эпициклоиду со для головки. Если колеса вращаются по направлению стрелок и ведущее колесо есть В, то ножка его зуба будет вести головку зуба колеса А да линии центров АВ и на точке m ножка зуба колеса В оставит головку зуба колеса А. Если начало соприкосновения происходить в точке о, то по предыдущему высота головки зуба колеса А будет fo. Точка соприкосновения будет перемещаться по дуге mо, которая = dm = cm и будет дугой зацепления до линии центров. Кривая omn будет полной дугой зацепления. Ясно, что полная дуга зацепления должна быть длиннее шага колеса, так как иначе зацепление одной пары зубьев кончится раньше, чем пойдет в зацепление следующая пара, и передача будет нарушена. Если диаметр образующего круга взять равным радиусу начальной окружности, в которой он помещается, то гипоциклоиды в таком случае обращаются в прямые, проходящие черев центр колеса, и ножки зубьев   будут очерчены прямыми; такие зубья называются прямобочными. Если одно колесо должно сцепляться с несколькими другими колесами, то ясно, что диаметр образующих кругов, при вычерчивании профилей зубьев у этих колес, должен быть один и тот же.

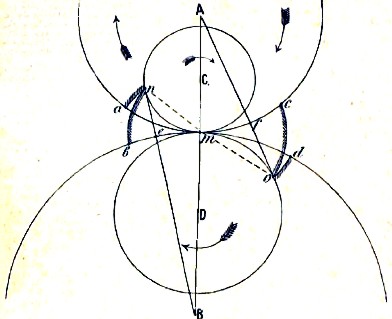
Рис. 7

Цевочное зацепление. Если мы возьмем диаметр образующего круга равным диаметру начальной окружности, т. е. начальную окружность обратим в образующий круг, то точка m на одном колесе все время будет совпадать с начальной окружностью, и профиль зубцов на этом колесе будет точка m, а на другом колесе точка m опишет эпициклоиду, которая и будет представлять профиль зубьев для этого колеса. Так как в виде точки зубцов выполнить нельзя, то их выполняют в виде цилиндров, которые называются цевками, а профили другого колеса вычерчивают, проводя кривые, параллельные эпициклоидам, на расстоянии, равном радиусу цевки. Совершенно так же, как для внешнего, могут быть вычерчены циклические профили зубьев для внутреннего зацепления.

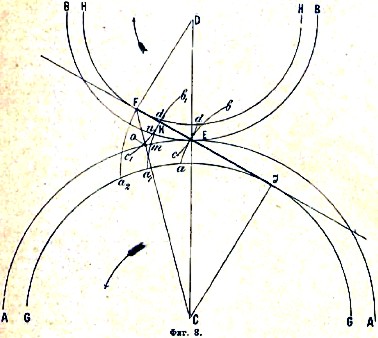
Рис. 8

Развертывающая окружности как профиль зубьев. На фиг. 8 АА и ВВ начальные окружности колес, касающиеся друг друга. Проведем через Е под произвольным углом (обыкновенно 72°—76°) к линии СD прямую FJ. Опустив из С и D перпендикуляры CJ и DF, проведем касательные окружности радиусами СJ и DF. Начертим точкой Е прямой EJ развертывающую ab окружности GG и концом Е отрезка EF развертывающую cd окружности ПП. Взяв на линии EF еще одну точку К, начертим развертывающие a₁b₁ и с₁d₁. По свойству развертывающих  1) кривая а₁b₁ может быть рассматриваема как кривая аb, повернутая вместе с кругом АА около его центра С на угол aCa₁, точно так же кривая c₁d₁ может быть рассматриваема как кривая cd, повернутая около центра D на угол dDd₁; 2) кривые ab и cd, и a₁b₁ и с₁d₁, касаясь взаимно, первые в точке Е, а вторые в точке К, имеют нормалью линию FJ, проходящую через точку Е прикрепления начальных окружностей; 3) дуга dd₁ равна отрезку КЕ, который также равен дуге аа₁ а потому аа₁ = dd₁. Означим угол аСа₁ через Θ₁, а угол dDd₁ через Θ₂; тогда аа₁ = Θ₁. CJ и dd₁ = Θ₂. DF. Если обозначим радиус окружности АА—R₁, а окружности BB-R₂, то по предположению, что ab неизменно соединена с АА и cd — с ВВ, будем иметь: дуга mЕ = Θ₁.R₁ и дуга nЕ = Θ₂.R₂; но из подобия треугольников FDE и CEJ следует:

FD/DE = CJ/CE или CJ/R₁ = FD/R₂, а потому дуга аа₁/дуга Em = CJ/R₁ = FD/R₂ = дуга dd₁/дуга En или aa₁/Em = dd₁/En, что по равенству aa₁=dd₁ дает Em=En, а это убеждает нас в пригодности развертывающей окружности для профиля зубьев, так как это равенство указывает, что при скольжении друг по другу кривых ab и cd, вращающихся около неподвижных центров С и D, скорости на окружностях АА и ВВ, неизменно соединенных соответственно с кривыми ab и cd и касающихся в точке Е, будут равны между собой.

Рис. 9

Из чертежа видно, что при вращении колес по направлению стрелок точка прикосновения зубцов не может идти дальше F. Соединив F с С, получим на окружности АА наиболее возможную высоту зубцов (FO) колеса С. Зацепление начнется в точке J и окончится в точке F; точка соприкосновения зубьев все время будет передвигаться по линии FJ, и эта линия будет линией зацепления.

Рис. 10

Зубцы, имеющие профиль развертывающей, выгодны тем, что оси колос могут быть несколько раздвинуты, причем правильность зацепления не изменяется (свойство развертывающей); при циклическом же зацеплении нужно очень точно устанавливать расстояние между зубьями. С другой стороны, зубцы, очерченные по развертывающей, соприкасаются всегда выпуклыми поверхностями, а у циклических колес выпуклая поверхность соприкасается с вогнутой, вследствие этого, при всех других равных условиях, давление на единицу поверхности зуба у колес с профилем по развертывающей больше, а потому такие колеса быстрее срабатываются, причем их профиль получает очертание, приближающееся к циклическим кривым, и вместе с этим утрачивается и вышеуказанное преимущество развертывающей. Кроме того, как показывает исследование, существующее в колесах трение при циклическом зацеплении меньше, чем при развертывающем, ввиду этого при точных установках всегда делаются колеса с циклическим профилем.

Если требуется передать движение между пересекающимися валами, тогда зубцы нарезаются не на цилиндрической поверхности. а на конической, и получаются конические зубчатые колеса (фиг. 9). Для того, чтобы передача происходила при постоянном отношении угловых скоростей, профили зубьев должны удовлетворять тем же условиям, как и в цилиндрических колесах.

При передаче движения между валами не параллельными и не пересекающимися применяются так называемые винтовые колеса (см. винт).

Исследования показывают, что между зубцами зубчатых колес, всегда происходит трение, на что затрачивается работа. Эти потери, для каждой пары колес, при хорошей обработке зубьев достигают 3%, а при плохой до 10%.

Зубья могут получаться отливкой, после чего они обрабатываются вручную, или же могут нарезаться на особых зуборезных машинах (специальные фрезовые и строгальные); в последнем случае зубья получаются более точными, а потеря работы на трение достигает минимальной величины. Чтобы сообщить зубьям более главное зацепление и большую прочность, их делают иногда в виде ломаной линии (фиг. 10). Такие зубья называются елочными, или шевронными.

Маховые колеса представляют массивные кольца, соединенные со ступицей при помощи спиц или сплошного диска, и назначаются для уравнивания хода машин. Неравномерность хода машины замечается в тех случаях, когда работа двигателя становится больше или меньше работы сопротивления, т. е. работы машины. Так как при вращении махового колеса центр тяжести его не перемещается, то весь избыток или недостаток работы двигателя идет на увеличение или на уменьшение новой силы маховика; последний служит как бы резервуаром  в котором накопляется избыток работы двигателя и затем снова отдается в те моменты, когда работы двигателя недостает. Чем тяжелее маховое колесо, тем в меньших пределах будет изменяться скорость машины при той же разнице в работах двигателя и сопротивлении. Но произвольно увеличивать вес маховика не следует, так как при этом увеличивается работа трения в подшипниках вала и понижается коэффициент полезного действия машины. Также необходимо обращать внимание на то, чтобы окружная скорость обода маховика не достигла слишком большой величины, так как при этом, вследствие центробежной силы, маховик может быть разорван, что может привести к большому несчастью; бывали случаи, когда куски разорвавшегося маховика пробивали крышу и стены здания и вылетали на двор, причиняя смертельные случаи. Если маховик приготовлен из чугуна, то окружная скорость на ободе не должна превосходить 30 метров в сек.

А. Гавриленко.