Кристаллическая структура

Кристаллическая структура есть понятие, относящееся к расположению частиц кристаллического вещества. Оно зародилось вместе с другими основными понятиями научной кристаллографии и приняло определенную форму в представлении основателя научной кристаллографии Гаюи. Но он, при недостаточности имевшегося еще тогда научного материала, связал это представление с представлением той формы, которая получается из однородного кристаллического вещества раскалыванием по плоскостям спайности, и этим впал в противоречие, так как в результате часто получаются формы, из которых нельзя сложить кристаллическое тело. Например, флюорит (плавиковый шпат) раскалывается на правильные октаэдры, которые нельзя сложить в одно сплошное вещество.

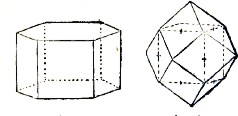
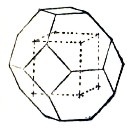
Такие тела, из которых, и притом в параллельном положении, можно выполнить пространство без промежутков, впервые получили полный геометрический вывод в «Началах учения о фигурах» Е. С. Федорова и названы параллелоэдрами (1880). По существу их можно свести к четырем основным типам, из которых один соответствует общеизвестной фигуре — кубу, а три остальные — гексагональная призма, ромбический додекаэдр и притупленный октаэдр — представлены на фигурах 1, 2 и 3. Так как каждое такое геометрическое тело всегда ограничено равными параллельными гранями попарно, то, соответственно числу пар параллельных граней, их общнее называть трипараллелоэдром (куб), тетрапараллелоэдром (гексагональная призма), гексапараллелоэдром (ромбический додекаэдр) и гептапараллелоэдром (притупленный октаэдр). Из фигуры 2 видно, что центры граней расположены как середины ребер куба, а из фигуры 3 видно, что центры граней (октаэдра) расположены как вершины куба. Обратим внимание на то, что в ромбическом додекаэдре 14 вершин, из которых в шести сходится по четыре, а в восьми — по три грани. Первые называются тетрагональными, а вторые тригональными. Первые шесть вершин можно рассматривать как вершины октаэдра, последние восемь — как вершины куба.

Фиг. 1.2

Фиг. 2.

Если бы выполнили пространство такими телами и задались бы вопросом о расположении точек, например, составляющих их центры, то получили бы пространственные решетки: точки эти располагались бы на равном расстоянии на прямых линиях (конгруэнтные ряды), а на плоскостях вообще образовали бы систему равных параллелограммов (плоских сеток)¹⁾. К такому представлению о расположении частичек кристалла, рассматриваемых как точки, подходили Зеебер (1824), Делафосс (1843), но наиболее систематически ими занялись Франкенгейм (1835-1842) и Бравэ, в сочинении которого «Мémoire sur les systèmes formés par de points distribués régulierèment sur un plan ou dans l’espace» (1850) сделан их полный вывод.

Фиг. 3.

Необходимость такого представления вытекала не только из закона Гаюи (см. кристаллография), который без него был бы непонятен, но и на основании изучения физических свойств, особенно свойств оптических, законы коих раскрылись с полной ясностью Френелем.

¹⁾ Впоследствии в «Reguläre Plan- n. Raumtheilung» (1906) Федоровым показано, что, сохраняя правильность в расположении, эти паралледоэдры, как ячейки, могут быть разнообразно ориентированы, и таких предусматриваемых расположений оказывается 754 для трипараллелоэдров, 358 для тетрапараллелоэдров, 217 для гексапараллелоэдров и 208 для гептапараллелоэдров.

Оказалось, что свойства сохраняют замечательное постоянство по прямым линиям любых направлений и изменяются с изменением этих направлений в вполне однородных кристаллах; при малейшем, можно сказать, самом ничтожном нарушении этой однородности, даже при простом сдавливании кристалла проявление однородности по одному направлению прекращается. Ничтожный поворот, то есть вывод частиц из параллельного положения, уже дает себя знать в изменении распределения физических свойств.

Из этого представления вытекает «заключение о весьма неодинаковом структурном значении разных, появляющихся на кристалле граней, в зависимости от плотности расположения точек для данной грани. Этот вывод получил полное подтверждение применением статистического метода, а именно оказалось, что преобладающее значение при развитии форм каждого кристалла имеют те грани, которым принадлежит наибольшая плотность. Физическая причина этому найдена в наибольшей растворимости граней, так как грани более слабой растворимости при процессе кристаллизации зарастают (хотя и очень медленно; часто процессы тянутся месяцами). Таким образом, была установлена связь между структурой кристалла и статистическим значением (частым проявлением) каждой данной грани, и явилось возможным установить (хотя только с известной степенью вероятности) структуру каждого изучаемого кристалла.

Структуры, соответственно параллелоэдрам, названы гексаэдрической (гексаэдр — куб), призматической, додекаэдрической и октаэдрической. Для призматической структуры расположение точек вполне ясно по взаимному расположению выполняющих пространство гексагональных призм. Кристаллы, удовлетворяющие этому условию, выделены в особый тип —  гипогексагональный. Кристаллы трех других видов структуры оказываются настолько тесно связанными между собой, что иногда нелегко вывести, к какой именно из этих структур относится расположение их точек, почему они соединены во второй — кубический тип. Чтобы наглядно себе представить различие в расположении точек этих трех структур, нужно вообразить себе куб; в гексаэдрической структуре точки располагаются как вершины этого куба, в октаэдрической структуре к этим точкам следует присоединить еще центр, а в додекаэдрической структуре, кроме центра, нужно вершины куба заменить серединами его ребер.

Установление структуры оказалось совершенно необходимым, чтобы придать точность самому понятию о форме кристалла и при переменности его комбинаций извлечь присущее ему постоянство, которое можно облечь в форму чисел, совокупность которых, при соблюдении известных условий, составляет символ комплекса. Так как эти числа, в свою очередь, можно расположить по порядку важности, и все символы комплекса в строгом порядке занести в таблицы, то ясно, что на этом можно основать распознавание веществ кристаллов, что и составляет сущность кристаллохимического анализа. Однако, из изложенного видно, что числа, кладущиеся в основу символов комплекса, имеют статистическое основание, то есть не достоверны, а только вероятны. Естественно, что наука ожидает появления метода, который дал бы возможность делать относительно структуры кристалла достоверные выводы. Надежды на появление такого метода связались со сделанными по инициативе Лауе опытами фотографирования кристаллов после пропускания через них очень узкого пучка рентгеновских лучей. Опыты эти были впервые произведены летом 1912 года Фридрихом и Книппингом и описаны в статье «Interferes - Erscheinungen bei Röntgenstrahlen» в «Sitzungsber. bayer. Akad. Wiss». S. 303, а первая теория этого явления дана Лауе в той же книжке, стр. 363.

Поразительные результаты дифракции рентгеновских лучей кристаллами вызвали необыкновенный интерес физиков и производство многочисленных новых опытов и теоретических объяснений. Между появившимися работами особенное значение получили работы Брагга, не только существенно изменившего теоретическое объяснение Лауе, но и введшего новые опыты отражения от кристаллов однородных рентгеновских лучей, получаемых заменой платиновых электродов родиевыми. При отражении однородными лучами можно было измерять энергию отраженных и вместе с тем интерферирующих лучей разных порядков, и в разных случаях энергия лучей разных порядков оказалась весьма различной, что дало в руки нить для важных заключений о расположении и абсолютном расстоянии отражающих плоскостей, представляющих, собственно, плоскости расположения частиц (скорее даже атомов) кристалла, то есть того, что в кристаллографии получило название плоских сеток. Первые появившиеся статьи были: «The diffraction of short electromagnetic waves by а cristal» («Proceed. of the Cambridge philos. soc.», XVII, 43), «The structure of some cristals as indicated by their diffraction of Х-rays» и «The structure of the diamond» (обе в «Proceed. of the Royal soc.», 89, 248 и 277).

В результате оказалось, что изображение, получаемое на фотографической пластинке, само по себе представляет определенную проекцию комплекса (гномоэллиптическую; см. кристаллографические проекции), что главным действующим фактором при этой дифракции являются атомы, а именно атомы с наибольшим весом, и что эти атомы слагают пространственные решетки и не только простые, но и сложные.

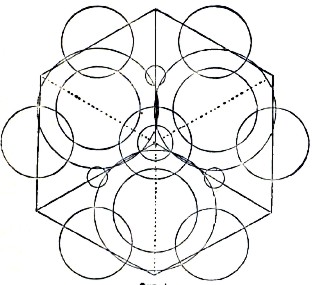
Результаты, к которым пришли физики Брагг относительно строения алмаза, наглядно представлены на фигуре 4 посредством кругов, коих центр указывает на тот перпендикуляр, на котором находится изображаемый атом углерода, а величина радиуса (уменьшенного в четыре раза) указывает относительное расстояние этой точки от плоскости чертежа. На этой фигуре, прежде всего, виден куб, три грани которого сходятся в центральной точке; ближайшие к плоскости чертежа есть те три точки, которые находятся на серединах ребер, сходящихся в этой точке, затем шесть точек находятся в одной плоскости, параллельной плоскости чертежа, и занимают положение середин шести ребер куба, и в той же плоскости располагается и центр куба; наконец, дальше на том же расстоянии располагаются три точки на серединах остальных ребер куба (задних).

Фиг. 4.

Однако, кроме этих точек, внутри куба располагаются еще четыре точки несколько ближе к плоскости, чем соответствующие середины ребер (одна из них посредине между центром куба и передней вершиной). Они образуют особый правильный тетраэдр. Таким образом, точки располагаются близкими парами и обусловливают две близкие пространственные решетки додекаэдрической структуры (см. выше). Можно ли эти пары точек принять за кристаллическую частицу алмаза, решит будущее. Последними успехами в этой области можно считать определения положения атомов в ряде минералов и искусственно полученных кристаллах, сделанные В. Л. Браггом в последней его работе «The analysis of crystals by the Х-ray spectrometer». В цинковой обманке ZnS расположение атомов совершенно такое же, как в алмазе, но положение вершин особого тетраэдра принадлежит атомам S (серы), а атомы Zn (цинка) занимают положение остальных атомов углерода в алмазе. Мы можем легко представить себе это положение из формы ромбического додекаэдра (фигура 2), если вообразим себе, что в его центре находится атом Zn, а в четырех тригональных вершинах (составляющих тетраэдр) атомы S. В плавиковом шпате CaF₂ в центре находится атом Са (кальция), а во всех восьми тригональных вершинах — атомы F (фтора). В каменной соли, NaCl, атомы расположены как вершины куба, причем, если в одной из них находится атом Na (натрия), то в трех ближайших помещаются атомы Сl (хлора). Таково же расположение атомов и в кристаллах солей BrNa (бромистого натрия), СlК (хлористого калия), ВrK (бромистого калия) и проч. Все эти соли кристаллизуются в кубиках, а по плоскостям их они очень легко раскалываются (весьма совершенная спайность). Наиболее интересное и сложное строение оказалось в кристаллах серного колчедана FeS и близких к ним. Эти, теперь определенные на опыте, структуры вполне совпали с теми, которые в полноте были предусмотрены около четверти столетия тому назад (заметки по этому поводу опубликованы Е. Федоровым в «Записках Горного Института» и в «Zeitschrift für Kristallographie»).

Е. Федоров.