Кватернионы

Кватернионы, комплексные числа вида d+ai+bj+ck, где d, а, b, с — вещественные числа, коэффициенты кватерниона, а l, i, j, k четыре основных единицы, умножение которых подчиняется следующим законам:

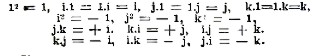
Как вещественные, так и обыкновенные комплексные числа вида d + а√-І или d + аi могут быть рассматриваемы, как частный случай кватернионов — первые при а = b = с = 0, вторые при b = с = 0.

Кватернион состоит из двух частей — скалярной части, или скаляра d и векториальной части, или вектора ai+bj+ck (см. векториальный анализ). Изображая числа а, b, с как отрезки на трех взаимно перпендикулярных осях, или, что то же, как координаты некоторой точки относительно тех же осей, мы можем рассматривать векториальную часть аи ai+bj+ck, как символ или числовое изображение некоторого вектора, именно, того вектора, который соединяет начало координат с точкой (а, b, с), определяемой координатами а, b, с. Скалярная часть d представляет число, не имеющее прямого геометрического значения; некоторые предлагают смотреть на скаляр d, как на некоторую числовую характеристику, связанную с вектором ai+bj+ck. Величина √a²+b²+c²+d² называется тензором кватерниона. Два кватерниона равны между собой, когда их соответственные коэффициенты попарно равны, так что равенство d+ai+bj+ck = d¹+а¹i+b¹j+с¹k равносильно совокупности, или системе четырех равенств d=d¹ а=а¹, b=b¹, с=с¹.

Правила сложения и вычитания кватернионов такие же, как и для обыкновенных комплексных чисел, именно сложение и вычитание кватернионов производится через сложение или вычитание их соответственных коэффициентов:

Умножение кватернионов производится по общим правилам умножения обыкновенных чисел, но произведения единиц l, i, j, k определяются приведенной выше таблицей. Отсюда можно видеть, что умножение кватернионов подчиняется закону сочетательному, т. е. для всяких трех кватернионов, А, В, С имеем (А.В).С=А.(В.С), и распределительному, т. е. (А+В).С=(А.С)+(В.С) и С.(А+В)=(С.А)+(С.В); но умножение кватернионов не подчиняется закону переместительному, т. е. для двух  кватернионов, А, В, произведение А.В вообще не равно В.А.

Деление кватернионов всегда возможно, если только делитель не равен нулю. Это следует из того, что каждому кватерниону А, не равному нулю, соответствует один вполне определенный кватернион 1/А или А^-1, дающий в обоих произведениях с А единицу: 1/А. А = А . 1/А = 1.

Значение кватернионов в математике и ее приложениях к механике и теоретической физике основано не только на том, что кватернионы имеют простой геометрический смысл, но и на том, что действия с кватернионами, в частности умножение на кватернионы, также представляют определенные геометрические действия. Вследствие этого кватернионы, имеют двоякое геометрическое значение — как величины и как операторы, так что посредством кватернионов действия над геометрическими величинами могут быть выражены при помощи действий над символами числового характера — кватернионами.

Пусть мы имеем в пространстве вектор А. Если начальная точка вектора остается неподвижной, то мы можем изменять вектор, вращая его около начальной точки и изменяя его длину. Это изменение, или преобразование вектора можно представить как его умножение на некоторый кватернион. Пусть мы имеем вектор А, которого длина, или тензор, равна ρ, а направление определяется тремя его углами α, β, γ, с осями i, j, k (см. выше); по предыдущему, этот вектор представится в виде ρ (i cosα + jcosβ + k cosγ). Повернем вектор А на угол ω около перпендикулярной к нему оси, образующей с осями i, j, k углы а, b, с, и вместе с тем изменим его длину из ρ в ρ¹. Оказывается, что эти изменения можно представить как умножение вектора А на кватернион.

М = ρ¹/ρ[cosω + sinω (i cosa + j cosb + k cosc)],

так что новый вектор А¹ изобразится произведением  

ρ¹/ρ[cosω + sinω (i cosa + j cosb + k cosc)]∙ρ(i cosα + j cosβ + k cosγ).

Здесь следует заметить; что, по примеру Гамильтона, при умножении кватернионов множитель ставится обыкновенно на первое место. Легко убедиться, что кватернион—множитель М имеет тензор ρ¹/ρ который показывает, в каком отношении первоначальный вектор А удлинился, или вытянулся при переходе в новое положение А¹ — отсюда и самое название тензор. Самый кватернион  М можно рассматривать как произведение его тензора ρ¹/ρ на кватернион

cosω + sinω (i cosa + j cosb + k cosc),

обусловливающий вращение вектора А около оси (а, b, с) на угол ω, и называющийся версором. Так как каждый кватернион  можно представить как произведение его тензора на его версор, то геометрически умножение на кватернион  представляет удлинение и поворот около оси кватерниона (вектора i cosa + j cosb + k cosc) на некоторый угол ω такого вектора, направление которого перпендикулярно к оси кватерниона. Значение векторов в геометрии, механике и теоретической физике основано главным образом на этом простом геометрическом истолковании умножения кватернионов (ср. VIII, 159/160). В 1895 г. была основана международная ассоциация для содействия изучению кватернионов и близких им математических систем.

См. Ромер, «Основные начала метода кватернионов», 1867; Сомов, «Векториальный анализ», 1907; Клиффорд, «Здравый смысл точных наук», 1910; Чезаро, «Алгебраический анализ», 1913; Laisout, «Introduction а la theorie des Q.», 1881; Molenbrock, «Theorie der Q.», 1891; Joly, « А manual of Q.», 1905.

Б. Млодзиевский.