Логарифмы

Логарифмы.

Не всякой формуле y = a^x, выражающей результат возведения в степень какого-нибудь числа, имеются три величины: число а, возводимое в степень; показатель степени х; и степень y. Всякое число y может быть представлено, как некоторая степень х другого числа и  в таком случае х называется логарифмом числа y при основании а. Если в то же время y может быть выражено как степень x’ другого числа b, т. е. если y = b^x’ , то x’ будет логарифмом числа y при основании b. Отсюда следует, что логарифмом какого-нибудь числа при некотором основании называется показатель степени, в которую надо возвести основание, чтобы получить данное число. Каждое число может, стало быть, иметь бесконечное число логарифмов, в соответствии с бесконечным числом возможных оснований. Логарифм принято означать символом lg, причем основание часто пишется внизу с правой стороны этого символа; таким образом, если y = a^x = b^x’, то lg_ay = x, lg_by = x’. Эти формулы могут вместе с тем писаться следующим образом:

Пусть y = a^x, и y’ = a^x’. Умножение и деление этих равенств дает формулы

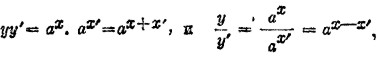
стало быть:

Кроме того

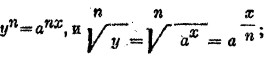
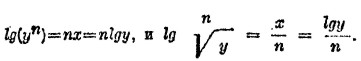
Эти отношения выражают четыре основных свойства логарифмов: 1) логарифм произведения равен сумме логарифмов множителей; 2) логарифм частного равен разности логарифмов делимого а делителя; 3) логарифм степени какого-нибудь числа равен произведению логарифма этого числа на показателя степени; 4) логарифм корня какого-нибудь числа равен частному от деления логарифма этого числа на показателя корня. Во всех этих формулировках предполагается, что основание в операциях берется одно и то же. Из приведенных свойств логарифмов вытекает возможность замены умножения сложением, деления вычитанием, возвышении в степень умножением, а извлечения корня делением: операции между числами заменяются операциями между их логарифмами, а потом по логарифму результата находят самый результат. В этом и заключается существенное значение логарифмов.

Логарифмы чисел, а также тригонометрических функций (синуса, косинуса, тангенса, котангенса) даются в таблицах логарифмов. За основание логарифмов берется либо число 10 (в десятичных, или бригговых, логарифмах), либо иррациональное число е=2,7132818284.., о котором речь будет ниже (в натуральных, или гиперболических, логарифмах). Каково бы ни было основание логарифмов, из равенств а⁰=1, а¹=а вытекает, что логарифм единицы при всяком основании есть нуль, а логарифм самого основания равен единице. Вместе с тем ясно, что логарифм числа, большего, основание, превышает единицу, тогда как логарифм числа, меньшего, чем основание, есть правильная дробь, — при предположении, что в обоих случаях само основание больше единицы.

Так, 4^1/2 = √4 = 2; 4^3/2 = √4³ = 8, и потому

lg₄8 = 3/2 = 1,5; lg₄2 = ½ = 0,5.

Остановимся теперь подробнее на логарифмах при основании 10. Что вытекает из формулы 10^х = у? Здесь может быть три случая:

1) у = 10ⁿ, где n — целое число, равное единице или большее единицы, и тогда х равно этому целому числу n;

2) у = 10^-n, где n — целое число, равное единице или большее единицы, и тогда х = -n, т. е., х выражается отрицательным целым числом;

3) у не может быть представлено в виде 10ⁿ, где n — целое число, положительное или отрицательное, и тогда х не может быть выражено ни целым, ни вообще конечным числом, а лишь дробным числом, положительным или отрицательным, с бесконечной дробью. Отсюда следует,  что, при основании 10, логарифмы могут быть точно выражены лишь в виде положительного или отрицательного целого числа, а именно для чисел, изображаемых единицей с нулями, или десятичных дробей, изображаемых единицей с нулями впереди. Логарифм числа, изображаемого единицей с нулями, равен числу нулей; а логарифм десятичной дроби, изображаемой единицей с нулями впереди, равен числу нулей до первой значимой цифры (считая и ноль перед запятой) с знаком минус. Так, lg 10000 = 4, а lg 0,00001 = —5, или, как еще пишут., =/5 . Логарифм всякого другого  числа выражается приближенно десятичной дробью, в которой берут, например, 5, или 7, иди 10 десятичных знаков. При этом целое число логарифма, стоящее с левой стороны запятой, называется характеристикой, а десятичные знаки, стоящие с правой стороны запятой, называются мантиссой логарифма. Из предыдущего следует, что характеристика логарифма всякого числа, большего единицы,  равна числу цифр целого числа минус единица.

Так, Іg8 = 0,…..; Іg 3429 = 3,…..; Іg 587,34 = 2,….

Что касается десятичных дробей, меньших, чем единица, то удобно писать их таким образом, чтобы мантисса оставалась положительной, а лишь характеристика была отрицательным числом. Возможность эта основана на том, что логарифмы двух чисел, находящихся в отношении 10ⁿ (n целое), отличаются характеристиками, но не мантиссами; в самом деле, если

y = a.10ⁿ, то lgу = lgа + lg(10ⁿ) = lga + n, lgy – lga = n.

т. е., два логарифма  различаются целым числом n. Отсюда видно, что логарифм всякой десятичной дроби имеет мантиссу, которая не отличается от мантиссы логарифма числа,  получаемого от десятичной дроби, если отбрасывается запятая. Что же касается характеристики десятичной дроби, то она равна характеристике целой части дроби;, если  же целой части нет, то мантисса равна положительной мантиссе целого числа, получаемого при отбрасывании запятой, а характеристика равна отрицательному числу, заключающему в себе столько единиц, сколько нулей стоит перед первой значимой цифрой дроби, считая и нуль перед запятой. Так, логарифмы, чисел 325,73 и 0,000489 имеют соответственно характеристики 2 и 4, а мантиссами положительные числа, равные мантиссам логарифмов чисел .32573 и 489. Часто вместо отрицательных характеристик пишут положительные дополнения их до 10, с подразумеванием —10.

Так, lg2 = 0,30103; а lg0,02 = /2, 30103 = 8,30103 (—10).

После того, как выяснено, как определяются характеристики логарифмов целых чисел и десятичных дробей, и каким образом определение мантисс логарифмов десятичных дробей сводится на  определение мантисс логарифмов целых чисел, остается показать, как вычисляются мантиссы логарифмов целых чисел. Это вычисление может быть, прежде всего, сделано методом непрерывных дробей. Пусть требуется найти Іg2=х. Это значит искать корня показательного уравнения 10^x=2. Так как искомый логарифм х меньше единицы, то можно положить x = 1/z, где z>1. Мы имеем 10^1/z=2, откуда 2^z=10. Так как 2³=8 и 2⁴=16, то z заключается между 3 и 4, и можно положить z = 3 + 1/t, где t>1. Наше уравнение получает вид:

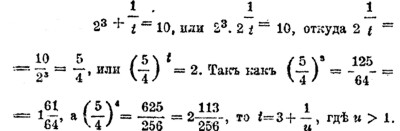
Продолжая подобным образом далее, мы можем получить логарифм числа 2 в виде непрерывной дроби:

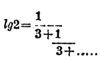
Можно взять столько звеньев непрерывной дроби, чтобы получилось желаемое приближение для величины логарифма. Данный метод  нахождения логарифмов требует кропотливых вычислений. В действительности же для вычисления логарифмов применяются формулы бесконечных рядов, связанные с теорией натуральных логарифмов.  Натуральные логарифмы еще называются неперовыми, так как они впервые были предложены Непером, изобретателем логарифмов. Они еще называются гиперболическими, на следующем основании: если в равносторонней гиперболе, отнесенной к ассимптотам, как осям, принять абсциссу вершины за единицу, то площадь криволинейной трапеции, заключенной между гиперболой, осью абсцисс и двумя ординатами — ординатой вершины и конечной ординатой  соответствующей абсциссе х, — выражается неперовым логарифмом logx (символ log часто служит обозначением неперова логарифма). В самом деле, уравнение равносторонней гиперболы может быть представлено в виде ху=1. Если разделить абсциссу, сторону криволинейной трапеции на р отрезков, возрастающих от вершины в геометрической прогрессии с  знаменателем отношения 1+α, то абсциссы будут

а соответственные ординаты будут

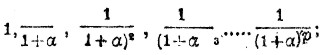
и расстояние между двумя последовательными ординатами будет

Если р очень велико, то узкую криволинейную трапецию между двумя последовательными ординатами, абсциссой и гиперболой  можно принять за прямоугольник, которого основанием есть ордината 1/(1+α)^Р, а высота α(1+α)^Р ; площадь подобного весьма малого прямоугольника будет, стало быть,

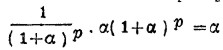
Площадь всей криволинейной трапеции, заключающей в себе р подобных прямоугольников, равна произведению рα. Но для конечной ординаты

х = (1+α)^Р, откуда lgx = plg(1+α), и, следовательно,

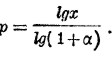
Искомая площадь выражается, стало быть, величиной

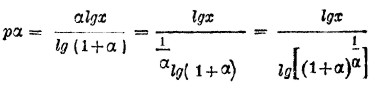
Если р бесконечно велико, то α бесконечно мало, и

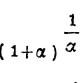
имеет пределом некоторое число е = пределу

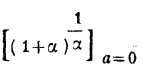
тогда формула lgx/lge выражает точно искомую площадь гиперболической трапеции. Если же за основание логарифмов взять число е, то loge = 1 и величина площади гиперболической трапеции выражается формулой logx/loge = logx, что и следовало доказать. Число е, или предел величины

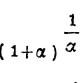
при бесконечно малом α, вычисляется при помощи бинома Ньютона:

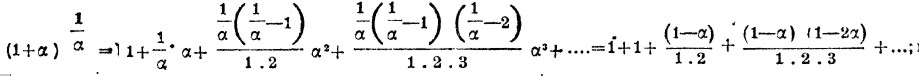
в предел, при α=0, е выражается бесконечным рядом

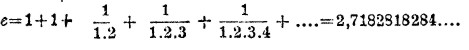
Вместе с тем нетрудно показать, что

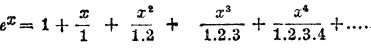
Выражает предел величины

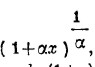
когда α стремится к нулю. Пусть теперь y = log(1+x), где х есть положительное или отрицательное количество, по абсолютной, величине меньшее единицы. Уравнение это дает

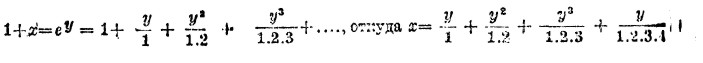
Чтобы найти, каким образом выражается y, как функция от х, можно представить y в виде бесконечного ряда

a₁x + a₂x² + a₃x³ + a₄x⁴ + ….

в котором величины а₁, а₂, а₃, а₄…. могут быть вычислены из предыдущего уравнения, по методу неопределенных коэффициентов, приравнивая нулю коэффициенты каждой степени х в уравнении

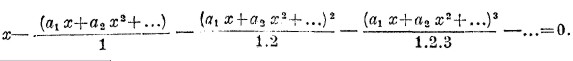
Отсюда получаются значения

а₁ = 1/1, а₂ = -1/2, а₃ = +1/3, а₄ = -1/4, и т. д.

Мы имеем, стало быть, формулу

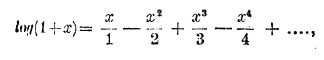
представляющую сходящийся ряд, если абсолютная величина х не больше единицы. Указанные формулы доказываются весьма просто и строго в дифференциальном и интегральном исчислении. Пусть х будет положительная дробь, меньшая единицы. Предыдущая формула дает

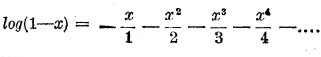
Вычитая эту формулу из предыдущей, мы получаем:

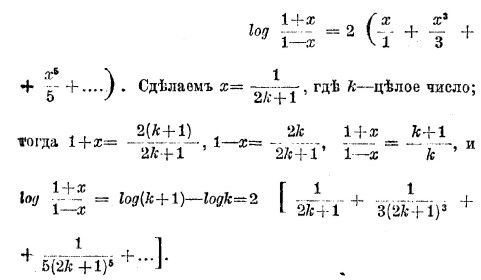
Последняя формула позволяет вычислить log(k+1), когда известен logk, при помощи быстро сходящегося ряда. Можно начать с

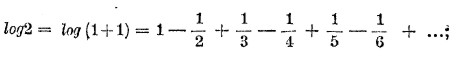
от 2-х восходят к 3-м, 4-м, и т. д., и таким образом могут быть вычислены неперовы логарифмы всех целых чисел. Как перейти теперь от неперовых логарифмов к бригговым? Существует весьма простая формула для перехода от логарифмов, вычисленных при одном основании, к логарифмам при другом основании. Пусть x=lg_lk; тогда k=І^х. Возьмем логарифмы обеих частей этого равенства при новом основании a; мы будем иметь

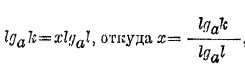
или

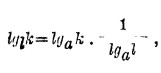
т. е. логарифм числа при основании I равен произведению логарифма этого числа при основании а на обратную величину логарифма основания I, вычисленного при основании а. Этот множитель

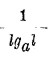
служащий для перехода от одной системы логарифмов к другой, называется модулем. При переходе от неперовых логарифмов к бригговым, модуль есть

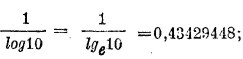
на это число надо помножить неперов логарифм, чтобы получить логарифм при основании 10. Подобным образом вычисляются всякие таблицы логарифмов. Покажем теперь на примере, как вычисляется помощью логарифмов какое-нибудь сложное выражение, заключающее в себе действия  умножения, деления, возвышения в степень и извлечения корня. Пусть требуется вычислить количество

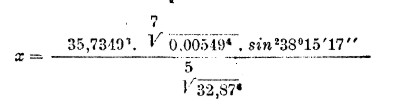
Перед тем, как логарифмировать это выражение, т. е. взять его логарифм, мы представим его в виде произведения только степеней — целых и дробных, положительных и отрицательных:

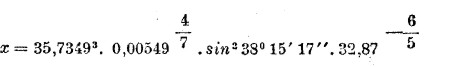
Логарифм этого количества выражается следующим образом:

При логарифмировании обыкновенно, ради простоты и единообразия, избегают вычитания логарифмов, а отрицательный логарифм заменяют его дополнением до 10 (подразумевая—10), что отмечается символом gonlg. Тогда искомый логарифм принимает следующий вид:

Вычислим теперь отдельные слагаемые этого выражения. В первом слагаемом Іg 35,7349 имеет характеристикой 1, а мантиссой — мантиссу числа 357349. Допустим, что у нас есть таблицы только 4-значных чисел. Вместо логарифма 6-значного числа 357349 будем искать логарифм числа 3573,49. Искомый логарифм заключается между логарифмами чисел 3573 и 3574. Таблицы дают мантиссу Іg 3573=55303, а мантиссу Іg 3574=55315; разность между обеими мантиссами составляет 55315—55303 = 12, причем эта разность соответствует разности чисел в 1  единицу. Допуская приближенно, что при небольших разностях чисел таковые пропорциональны разностям соответственных логарифмов, мы находим для мантиссы Іg 3573,49 сумму 55303 + 12·0,49 = 55303 + 5,88 = 55309. Итак, Іg 35,7349=1,55309. Помножая этот логарифм на 3, мы получаем 3·35,7349 = 4,65927. Переходя ко второму слагаемому, мы видим, что характеристика Іg 0,00549 равна 3, или 7—10; мантисса этого логарифма, равная мантиссе числа 549, дается таблицами, а именно 73957; следовательно, Іg 0,00549=7,73957—10. Чтобы найти произведение этого логарифма на 4/7, мы его умножаем сначала на 4, причем получаем 30,95828—40, а потом делим на 7, причем предварительно прибавляем 30 к вычитаемому и уменьшаемому для того, чтобы вычитаемое разделилось без остатка на 7; получаем   (60,95828-70)/7 = 8,70833—10. Мы имеем, стало быть, для второго слагаемого 4/7 Іg 0,00549 = 8,70833—10. Для вычисления третьего слагаемого мы прежде всего находим в таблицах Ig sin 38°15' = 9,79176(—10). Так как следующий логарифм Ig 38°16' = 9,79192, и разница между мантиссами для 1 минуты составляет 16, то для 17 секунд можно принять разницу пропорционально в 16·17/60 = 5 и Ig sin 38°15'17'' = 9,79181(—10). Помножая этот логарифм на 2, мы  получаем для третьего слагаемого 2 Ig sin 38°15'17 = 19,58362—20 = 9,58362 (—10). Переходя к четвертому слагаемому, мы видим, что характеристика Ig 32,87 равна 1; мантисса этого логарифма, равная мантиссе Ig 3287, дается таблицами: она равна 51680; следовательно, Ig 32,87 = 1,51680. Помножая этот логарифм на 6/5, мы получаем 6/5 Ig 32,87 = 1,82016. Дополнение этого  логарифма получается, если последнюю цифру справа вычесть из 10, а все остальные из 9:

gon 6/5 Іg 32,87 = 8,17984 (—10).

Таким образом, мы получаем следующую таблицу слагаемых:

Сумма этих слагаемых дает Іgх=1,13106. Остается теперь по логарифму результата найти число, или самый результат. Ищем в логарифмических таблицах и находим, что два последовательных логарифма с мантиссами 13098 и 13130, между которыми заключается мантисса нашего логарифма 13106, соответствуют числам 1352 и 1353. Разности чисел на единицу соответствует разность мантисс 13130—13098=32. Искомое число заключается между 1352 и 1353; оно превышает 1352 на дробь, составляющую такую же долю единицы, какую разница мантисс 13106—13098=8 составляет по отношению к разнице мантисс логарифмов 1353 и 1352, т. е. 8/32=0,25. Мантисса нашего логарифма соответствует, стало быть, числу 1352,25; а так как характеристика нашего логарифма есть 1, ибо Іgх=1,13106, то х=13,5225.

Таким образом, помощью логарифмов легко найден результат, который иначе мог бы быть получен лишь, путем крайне трудных вычислений, которые потребовали бы огромной траты времени.

Идея логарифмов, и основное свойство их были известны еще до Непера (М. Stieffel), и даже были составлены таблицы логарифмов, которые не были опубликованы (J. Byrge). Замечательно, что проекция географических карт Меркатора («морские карты»), в которой меридианы и параллели изображены системами параллельных линий, причем расстояния параллелей от экватора возрастают пропорционально натуральному логарифму тангенса полудополнения широты, была открыта Меркатором (Герардом Кауфманном) в 1569 году, задолго до изобретения логарифмов. Теорию этих карт, основанную  на суммировании секансов, дал, еще раньше появления  книги Непера, английский математик Райт (Wright) в 1589 году; теорема о расстоянии параллелей была  предложена Бондом (Bond) уже после изобретения логарифмов, в 1645 году, а впервые доказана она была Джемсом Грегори в 1663 году. Книга шотландского барона Джона Непера «Mirifici logarithmorum canonis descriptio» (John Napier) появилась на латинском языке в Эдинбурге в 1614 году. Название «логарифм» он составил из двух греческих слов λόγος, (слово, разум, отношение) и αριθμός (число). Книга отражает энтузиазм изобретателя.  Непер воображал движущееся тело, проходящее расстояния, изменяющиеся в геометрической прогрессии, когда время возрастает в арифметической прогрессии: расстояния были для него логарифмы времени. Тридцать три года спустя Грегуар де Сен-Венсан доказал, что если в гиперболе, отнесенной к асимптотам, площадь, заключенная между ординатой вершины, кривой и асимптотой, растет в арифметической прогрессии, как сумма равномерных кривых трапеций, то ординаты растут в геометрической прогрессии; это ведет к теореме о гиперболических площадях, как о неперовых логарифмах абсциссы. Немедленно после появления книги Непера, она обратила на себя внимание двух выдающихся математиков — упомянутого Райта и Генри Бригга. Первый перевел книгу Непера на английский язык, второй условился с Непером относительно перехода к системе логарифмов при основании 10. Непер умер в 1617 году. В этом же году появилась книга Бригга,  «Logarithmorum chilias prima», первое издание логарифмов при основании 10, всего в 60 страниц, in—8°. В 1624 году Бригг выпустил фолиант «Arithmetica  Logarithmica», в 300 страниц, в том числе 88 страниц введения и пояснений; книга эта заключала в себе логарифмы от 1 до 20 000 и от 90 000 до 100 000. Пробел был пополнен гентским математиком Адрианом Бланком. Бригговы логарифмы тригонометрических функций были впервые даны английским астрономом Эдм. Гунтером в книге «Canon triangulorum»  (1620), а потом (1628) Бланком в «Arithmetica logarithmica». Бланк дал логарифмы с 10 знаками.  Впоследствии появились труды Вега, Тейлора и Бремикера (7-значные логарифмы). Таблицы Лаланда дают 5-значные логарифмы.

Гауссом составлены таблицы для определения суммы и разности двух чисел по логарифмам этих чисел; это — гауссовы логарифмы.

Ю. Делевский.