Мажор

Мажор, общее выражение, объединяющее понятия: мажорный аккорд, мажорная гамма, мажорный лад (строй). Точно так же выражение «минор» объединяет понятия минорного аккорда, минорной гаммы, минорного лада (строя). Понятия мажора и минора в средневековой музыке не были еще ясно выражены и разграничены. Последним характеризуется только новая музыка (ХVIII-XIX вв.), гармония которой, а частью даже мелодиеобразование базируются на сопоставлении и противопоставлении этих двух основных акустических и художественных феноменов. Под мажорным аккордом (мажорным трезвучием) подразумевается одновременное сочетание трех тонов: основного (примы) и взятых от него вверх большой терции и чистой квинты. Мажорному аккорду свойствен основной характер света, радости, «твердости». Сочетание же основного тона (примы) и взятых от него вниз большой терции и чистой квинты дают аккорд минорный (минорное трезвучие: основной характер его — затемнение, печаль, «мягкость»).

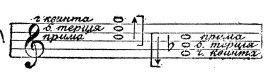
Пример 1.

Мажорный аккорд (мажорное трезвучие) может быть представлен и не всеми тремя своими тонами, а только двумя или даже одним, если только они воспринимаются нами в смысле этого аккорда (то есть как его составные элементы). Точно то же соответственно можно сказать и про минорный аккорд. Например, терция do-mi может входить и в состав мажорного аккорда do-mi-sol и в состав минорного аккорда la-do-mi. В зависимости от того, в смысле какого именно аккорда эта терция будет нами (в связи со всем предыдущим, и всем последующим) восприниматься, она и будет представлять трезвучие мажорное или минорное. Учение о гармонии, исходящее из понятий генерал-баса (см.), определяет мажорный аккорд, как аккорд, построенный вверх от основного тона, из двух терций, — большой и малой (то есть do-mi плюс mi-sol; см. пример выше); а минорный аккорда, как аккорд, построенный (тоже вверх от основного тона) из двух терций, — малой и большой (то есть fa-la бемоль плюс Іа бемоль — do). Происхождение мажорного аккорда (а с ним вместе и всей сущности гармонии) коренится в явлении, данном нам самой природой. Каждый звук человеческого голоса и наших музыкальных инструментов, как давно известно (и особенно хорошо исследовано Гельмгольцем), состоит из целого ряда простых тонов, более или менее различимых при напряженном внимании. Главный, самый сильный и слышный из этих тонов — нижний; от него звук получает и свое название. Все эти тоны называются обертонами (также тонами натуральными, гармоническими, парциальными, или частичными, аликвотными). Совокупность всех обертонов, создающих слышимый нами музыкальный звук, Риман называет созвуком (Klang). Если расположить все обертоны в порядке возрастающей высоты, то окажется, что число колебаний второго вдвое больше, чем первого (главного), третьего — втрое больше и т.д.

Пример 2.

Отношения между числами колебаний обертонов и числом колебаний главного тона образуют, таким образом, последовательный ряд чисел 1, 2, 3, 4 и т.д. Число обертонов не ограниченно, но чем они выше, тем звучат слабее, неуловимее и имеют меньшее значение для всего созвука. Ряд первых 16 обертонов созвука Do (большой октавы) изображен на примере 2.

Тоны, обозначенные белыми нотами, входят в состав мажорного аккорда, построенного на Do. Отсюда — мысль вывести музыкальное явление мажорного аккорда из акустического феномена созвука. В самом деле, исключим из этого ряда: 1) обертоны 7, 11, 13, 14 (со звездочками), как не совсем точно соответствующие высоте изображающих их нот;

Пример 3.

2) обертоны, обозначенные производными цифрами (9 = 3.3; 15 = 3.5; 25 и т.д.), как очевидно производные «обертоны от обертонов;

Пример 4.

3) все октавные удвоения (то есть 2, 4, 6, 8 и т.д.). По их исключении останутся только обертоны 1. 3. и 5, то есть те, которые образуют мажорный аккорд в широком положении (пример 5).

Минорный аккорд объясняется школой гармонических дуалистов (Эттинген, Риман и др.) подобным же образом; только здесь все частичные тоны (унтертоны) строятся вниз от основного тона, так что число колебаний 2-го унтертона вдвое меньше, чем число колебаний основного тона; число колебаний 3-го унтертона втрое меньше и т.д. Вот ряд унтертонов от do 2-й октавы (пример 4).

Если из этого ряда исключить (по тем же причинам, как и выше) унтертоны неточные (7, 11, 13, 14), производные (9, 15) и октавные удвоения, то получим унтертоны 1. 3. 5, дающие минорный аккорд в широком положении (пример 3).

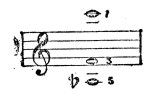
Пример 5.

Не следует, однако, забывать, что система унтертонов — не бесспорный, научно-исследованный феномен, как система обертонов; это только гипотетическое построение, практически и теоретически открывающее, однако, широкие горизонты. Мажорная и минорная гаммы, см. гамма. Мажорный и минорный строй, тональность, см. строй и тональность.

Ю. Энгель.