Механика

Механика (от греческого μηκανή — машина), наука, изучающая равновесие и движение физических тел. Сообразно с принятым в физике делением тел на твердые, жидкие и газообразные, нередко рассматривают в качестве отдельных научных дисциплин; а) механику твердого тела, б)  механику жидкостей, или гидромеханику, и в) механику газов, или аэромеханику. Кроме тел твердых, жидких и газообразных, в механике еще играет большую роль воображаемое тело, называемое материальной точкой. Это — такое материальное тело, все три измерения которого исчезающе малы. Если тело, действительно существующее в природе, удовлетворяет этому условию, то непременно будет ничтожно  малым и количество материи, в нем заключающееся: примером может служить атом. Однако в механике нередко воображают и такие материальные точки, в которых заключается значительное количество материи. Выгода, приносимая рассмотрением равновесия и движения материальной точки, заключается в большей простоте механических сил, сюда относящихся. Всякая совокупность материальных точек называется материальной системой. Любое тело есть материальная система. По характеру рассматриваемых явлений механика в  целом (а иногда также в отдельности механика материальной точки, механика твердого тела, гидромеханика и аэромеханика) делится на три части: кинематику, статику и динамику. Эти три части возникли не одновременно, развивались неодинаковыми путями и представляют собой как бы три самостоятельные науки.

Кинематика (от греческого κινημα — движение) рассматривает движение тел с внешней, геометрической стороны, не обращая внимания на физические причины, производящие это движение. Она не нуждается для своего изложения ни в каких постулатах или аксиомах, кроме аксиом математики; поэтому кинематику иногда называют «геометрией четырех измерений» (роль четвертого измерения играет время). Кинематика, как отдельная наука, установилась сравнительно недавно. Впервые Даламбер указал на важность изучения соотношений между временем и положением тел в пространстве; Кант в «Metaphysische Aufangsgründe der Naturwissenschaft» отстаивает, с философской точки зрения, право кинематики на существование в смысле самостоятельной науки под именем «форопомии». Ряд важных кинематических теорем был выведен Робервалем, Эйлером, Шалем; но только Ампер первый выяснил (в 1834 г.) необходимость того, чтобы изложению динамики предшествовала чисто геометрическая теория движения. В  1862 г. вышла в свет «Чистая кинематика» французского ученого Резали; тем самым  произошло окончательное установление кинематики, как самостоятельной научной дисциплины.

Предмет статики (от греческого корня sta — стоять) составляют два вопроса: 1) вопрос о равновесии тела под действием сил; 2) вопрос о замене одних сил другими, производящими то же действие. Из трех отделов механики статика является наиболее древним. Основателем статики был Архимед. Ему принадлежит,  между прочим, теория рычага, основанная на следующих двух положениях, принимаемых за аксиомы: 1) равные грузы, действуя на рычаг на равном расстоянии от точки опоры, находятся в равновесии; 2) равные грузы, действующие на неравном расстоянии от точки опоры, не дают равновесия, но тот из   них, который действует на большем расстоянии, перетягивает. Из этих предпосылок он путем чистого рассуждения выводит, что два груза находятся на рычаге в равновесии тогда, если величина их обратно пропорциональна их расстоянию от точки опоры.  Этим примером иллюстрируется тот важный факт, что в основе выводов статики лежат некоторые особые аксиомы, даваемые опытом. Выбор этих аксиом — различный у различных авторов. Статической аксиомой, наиболее богатой содержанием, является т. н. принцип возможных перемещений, установленный в общей форме Иоганном Бернулли и заключающийся в следующем: необходимое и достаточное условие равновесия системы состоит в том, что сумма работ внешних приложенных   сил для всякого возможного перемещения системы должна равняться нулю или быть меньше нуля.

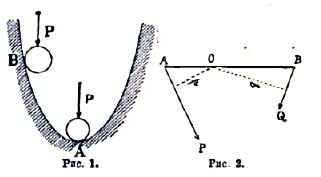
Рис. 1. Рис. 2.

Простой пример: пусть имеем внутри чашки (рис. 1) шарик, находящийся под действием вертикальной силы Р (например, силы веса шарика) и прикасающийся где-либо к поверхности чашки. Возможными перемещениями для шарика являются различные перемещения по поверхности чашки, а также перемещения, удаляющие его от этой поверхности. Но легко убедиться, что если представим себе шарик в какой-нибудь точке В, то среди возможных перемещений его будут такие, при которых работы силы Р больше нуля (это именно – перемещения книзу); только при нахождении шарика в самой нижней точке А работа силы Р будет нулем или отрицательной величиной для всех возможных перемещений шарика; итак, здесь и только здесь он будет в равновесии. Применим еще принцип возможных перемещений к выводу правила равновесия рычага. Пусть АВ (рис. 2) и будет рычаг, имеющий точку опоры в О и находящийся в равновесии под действием сил Р и Q, лежащих в плоскости чертежа. Возможным для нашего рычага перемещением будет вращение около точки О на бесконечно малый угол α. При таком перемещении точки А и В, служащие точками приложения сил, продвинутся по бесконечно малым дугам, длины которых будут АО.α и ВО.α. Сумма работ сил Р и Q при этом  будет выражаться формулой Р.АО.α.sin РАО — Q.ВО.α.sin OBQ. По принципу возможных перемещений, эта сумма есть нуль, откуда вытекает, что Р.АО.sin РАО — Q.ВО.sin ОBQ = О. Это и есть условие равновесия вашего рычага. Ясно, что произведения АО.sin РАО и ВО.sin OBQ соответственно равны длинам отрезков р и q, представляющих расстояния от точки опоры до направлении действующих сил; поэтому еще проще найденное нами условие равновесия рычага пишется так: Рр — Qq = о. Произведение силы на расстояние ее направления от точки опоры рычага, взятое со знаком + или —, смотря по тому, стремится ли данная сила вращать рычаг вправо или влево, называется статическим моментом, или просто моментом силы. Таким образом, условие равновесия рычага приобретает следующую форму: алгебраическая сумма моментов сил, действующих на рычаг,  должна быть нулем. Весьма важную роль играет в статике следующая аксиома: действие связей, стесняющих свободу движения тела, может быть заменено действием некоторых сил. Так, например, если некоторое тело имеет одну неподвижную точку, то мы можем рассматривать это тело, как вполне свободное, причем  лишь нужно считать, что к упомянутой точке приложена некоторая сила. Аксиома о замене связей силами имеет величайшее значение или практических применений механики к построению машин, также мостов, стропил и других конструкций. Так, силами связи здесь часто являются давления на опоры; их нужно знать для расчета прочности и устойчивости опор; определение этих сил производится на основании аксиомы, только что упомянутой. Нередко для разыскания условий равновесия различных систем пользуются следующей аксиомой: если система находится в равновесии, то равновесие ее не нарушается от наложения на систему новых связей, т. е. новых стеснений, ограничивающих возможные перемещения. Так, например, иногда, рассматривая равновесие системы, которая может изменять свою форму (как жидкость, гибкая нить и т. п.), находят удобным предположить, что система отвердела, или — точнее — сделалась вполне жесткой, «неизменяемой»; если до отвердения было равновесие, то оно и после отвердения не нарушается. Выгода такого предположения заключается в том, что к «неизменяемой» системе применяются условия равновесия твердого тела. Итак, вопросы о равновесии различных систем приводятся к простейшему случаю — к вопросу о равновесии твердого тела. Важнейшим отделом механики является динамика. Здесь изучается движение тел под действием сил; таким образом, в динамике мы имеем как бы синтез тех понятий и точек зрения, которые принадлежат, с одной стороны, кинематике, а с другой — статике¹⁾. Однако для того, чтобы этот синтез был возможен, необходимо с самого начала установить некоторые новые аксиомы (или, как их называют иначе, принципы), составляющие специальную принадлежность динамики. В первый раз две такие аксиомы были установлены Галилеем, вследствие чего он и считается основателем динамики. Первая из них называется принципом инерции и гласит, что материальная точка без действия внешних сил сохраняет свою скорость неизменной по величине и направлению; вторая называется принципом независимого действия сил и заключается в том, что силы действуют одинаково как на тело, находящееся в покое, так и на тело, находящееся в движении. Все вопросы, решаемые в динамике, сводятся к двум основным задачам: 1) по данным силам, действующем на тело при данных условиях, определить движение тела; 2) зная движение тела, найти силы, которыми это движение производится. Решение динамических задач упрощается благодаря ряду теорем, выводимых математическим методом в теоретической части динамики; из наиболее важных теорем мы назовем здесь две; теорему Даламбера и теорему живых сил. Первая из них указывает способ, посредством которого всякую задачу о движении можно трактовать, как задачу о равновесии; таким образом, вопросы динамики сводятся к вопросам статики, более трудное - к более легкому. Теорема живых сил изображает ту форму, в которой осуществляется в области механических соотношений закон сохранения энергии.

Большую важность имеют также: теорема о движении центра тяжести и теорема площадей. Когда система состоит из большого числа тел или отдельных материальных точек, то полное изучение ее движения может оказаться очень сложным и даже невыполнимым. В таких случаях, ранее подробного наследования движения частей системы, бывает полезно получить некоторое понятие об общем движении всей системы в совокупности. Для этой цели имеет особое значение определение движения центра тяжести системы. А именно оказывается, что центр тяжести свободной системы движется, как одна материальная точка, которая имеет массу, равную массе всей системы, и которая находится под действием всех сил, действующих на отдельные части системы. Например, представим себе бомбу, которая под действием тяжести летит по параболе и разрывается во время полета: тогда центр тяжести всех осколков будет после взрыва продолжать то же движение, какое он имел до взрыва.  

Теорема площадей указывает некоторую связь между движениями отдельных частей системы, могущей вращаться около некоторой оси. Так, например, если человек, стоящий на гладком полу с вытянутыми горизонтально руками, вертится около вертикальной оси и вдруг опускает руки, помещая их вдоль тела, то он чувствует, что его тело стало вращаться быстрее прежнего: здесь уменьшились площади, описываемые (в единицу времени) частями рук, но зато соответственно увеличились площади, описываемые остальным телом; общая же сумма площадей, описываемых (в единицу времени) всеми материальными точками тела, сохраняет прежнюю величину. Другой пример: если взять кошку за лапки и, держа ее висящей таким образом, выронить из рук, то она, падая, делает лапкой такие движения, которые за время падения сообщают ее телу поворот, нужный для того, чтобы ей упасть на лапки. Из числа основных теорем наиболее отвлеченной части динамики (так называемой аналитической динамики) назовем начало наименьшего действия²⁾.

¹⁾ Некоторые английские авторы (например, Кельвин и Тэт) динамику называют кинетикой; статику и «кинетику» объединяют под одним именем динамики; кинематику относят к чистой математике, а имя механики придают науке о машинах. Если иметь ввиду первоначальное значение слов (в частности, происхождение термина динамика от греческого δυναμις — сила), то нельзя не признать такую классификацию более логической.

²⁾ Действием называется двойная средняя живая сила системы за известный промежуток времени, умноженная на этот промежуток. Действие выражается формулой

^t1∫_t02Tdt,

где T = ½ ∑mv² есть живая сила системы, t – время. Так как сумма живой системы Т и потенциальной энергии системы U есть величина постоянная (T + U = h), то T = h-U, 2T = T-U+h; сделав, в выше написанном интеграле соответствующую замену, мы приблизим его к «форме Гамильтона».

Вот одна из форм (т. н. форма Гамильтона), в которой оно может быть представлено: если система тел в эпоху t₀ — имеет конфигурацию А, а в последующую эпоху t₁ конфигурацию В, то переход от первой конфигурации ко второй всегда совершается таким путем, что среднее значение разности между кинетической и потенциальной энергией системы за промежуток времени от момента t₀ до момента t₁ имеет минимальную величину.

Строго логическое изложение аксиом механики встречает значительные затруднения. Некоторые выдающиеся ученые (и в том числе Гельмгольц) делали попытки реформировать изложение механики о смысле приведения ее основных начал в форму, более удовлетворительную в логическом отношении. Из таких попыток особенно известна, сделанная Генрихом Герцем (см.). Герц ставит во главе своего изложения механики единственный основной принцип, представляющий обобщение принципа инерции и формулируемый так: всякая свободная система сохраняет свое состояние покоя или равномерного движения по прямейшему пути. Понятие прямейшего пути имеет у Герца следующий смысл. Представим себе точку, переходящую из одного положения в пространстве в другое. Мы можем составить себе совершенно ясное представление о ее траектории; если для нее по условиям, стесняющим перемещения, возможны различные траектории, то мы сумеем выбрать из них ту, элементы которой представляют наименьшую кривизну: такая траектория и будет прямейшим путем. Подобно этому определяется прямейший путь для системы, причем перемещением системы, по определению, считается квадратный корень из арифметического среднего квадратов перемещений отдельных точек системы. По Герцу, в природе существуют только связанные между собой системы, но не существует сил; если нам представляется система, движущаяся как будто под действием сил, то в действительности ее движение обусловливается связями ее с некоторыми другими системами, скрытыми от наших чувств (примером такой системы может служить эфир физиков). Надо сказать, однако же, что механика Герца представляет собой, по выражению Маха, «идеальную программу»; для применений же целесообразнее пользоваться обыкновенным строем изложения механики. Дальнейшего развития механика Герца до сих пор не получила.

Некоторые отделы механики имеют настолько большое теоретическое или практическое значение и при этом отчасти обладают настолько оригинальными методами исследования, что нередко рассматриваются и излагаются, как самостоятельные научные дисциплины. Сюда принадлежат: гидростатика, гидродинамика с аэродинамикой, теория притяжения и потенциала, гидравлика (см.), баллистика (см.), теория упругости с теорией сопротивления материалов, графическая статика, теория механизмов, теория машин.

I. Гидростатика. Гидростатика есть учение о равновесии жидкостей (капельных и газообразных) и о равновесии твердых тел, плавающих в жидкости. Основателем гидростатики является Архимед, написавший сочинение под заглавием  Περι κουμενων («О телах плавающих»), которое дошло до нас только в латинском переводе. Оно состоит из двух книг. В первой книге Архимед устанавливает следующие два принципа, которые он рассматривает, как данные опытом, и которые лежат в  основе всей его теории: 1) часть жидкости, менее сдавленная, выталкивается той, которая сдавлена более; при этом каждая часть всегда бывает сдавлена весом покоящегося на ней вертикального жидкого столба; 2) выталкивание жидкостью какого-нибудь тела кверху всегда происходит по направлению вертикальной линии, проходящей через центр тяжести выталкиваемого тела. Из первого принципа Архимед, прежде всего, заключает, что поверхность жидкости, все части которой тяготеют к земле, должна быть шарообразной при равновесии. Затем он выводит знаменитый закон, называемый его именем (см. жидкости, XX, 278/79). Из своего 2-го принципа Архимед выводит  законы равновесия плавающих тел; он доказывает, что плавающий сферический сегмент всегда располагается так, чтобы его основание было горизонтально. Во второй книге Архимед, исходя из тех же принципов, определяет положения равновесия плавающих тел, образованных вращением конических сечений; он рассматривает случаи, когда эти тела могут оставаться в наклонном положении, когда они должны держаться стоймя, и когда они должны опрокидываться или выпрямляться. Эта книга принадлежит к лучшим памятникам математического гения Архимеда.

Труды Архимеда по гидростатике нашли продолжение только в ХVI в., в руках голландца Стевина (1548—1620). Стевин первый применил Архимедовы положения к определению давления жидкости на дно и стенки сосуда, в котором она заключена, и к теории сообщающихся сосудов; он также открыл т. н. гидростатический парадокс; жидкость может давить на дно сосуда с силой, во много раз превышающей ее собственный вес.

В  сочинениях Архимеда и Стевина аксиомы и теоремы гидростатики излагались вне всякой связи с общими принципами статики. Галилей первый пытался установить эту связь, исследуя условия равновесия жидкостей в сообщающихся сосудах и другие вопросы на основании принципа возможных перемещений; впрочем, доказательствам Галилея недостает строгости. Более правильно был применен к гидростатике этот принцип Паскалем, который, между прочим, воспользовался им для доказательства т. н. «закона Паскаля» (см. жидкости).

Весьма значительным успехом гидростатика обязана Клеро, который впервые стал выражать ее законы с помощью дифференциальных уравнений (в 1743 г., в сочинении «Theorie de Іа figure de la Terre»). До Эйлера давление, действующее на какую-нибудь часть жидкости, обыкновенно рассматривалось, как вес некоторого находящегося над ней жидкого столба. Эйлер в мемуаре, появившемся в 1755 г., стал рассматривать давление, как силу, действующую на каждую частицу жидкости, вполне определяемую координатами этой частицы (а, следовательно, одинаковую во всех направлениях). При равновесии жидкости, разность сил давления, испытываемых какой-нибудь частицей с двух противоположных, друг другу параллельных сторон, должна равняться внешней силе, приложенной к частице по направлению, перпендикулярному к этим сторонам. Отсюда Эйлер получает дифференциальные уравнения гидростатики.

От этого способа отличается способ Лагранжа, который в своей «Меcanique Analytique» (1788) излагает гидростатику, как часть общей статики, исходя из начала возможных перемещений и из определения жидкости, как собрания частиц, обладающих свойством совершенной удобоподвижности. В настоящее время при изложении гидростатики большей частью пользуются методом Эйлера.

Из вопросов, рассматриваемых в гидростатике, упомянем в отдельности теорию равновесия плавающих тел и теорию вращательного движения жидкости. Теорию плавания в новейшее время разрабатывали Дюпен, Давидов, Буняковский, Слудский и др. Здесь весьма большое практическое значение (для мореплавания) имеет вопрос об устойчивости плавающих тел. В общем можно сказать, что равновесие плавающего тела является устойчивым, если центр тяжести тела, при отклонении последнего, оказывается лежащим ниже т. н. метацентра, т. е. точки, в которой вертикальная линия, проходящая через центр тяжести объема жидкости, вытесняемой отклоненным телом, встречается с направлением силы тяжести в теле при его равновесии.

Жидкость, находящаяся в равномерном вращательном движении и при этом не изменяющая своей формы, может быть рассматриваема, как покоящаяся, если приложить к ее частицам центробежную силу, на основании теоремы Даламбера. Если частицы вращающейся жидкости находятся только под действием взаимного притяжения по закону Ньютона, то жидкая масса может принять различную форму: сплющенного эллипсоида вращения, мало отличающегося от шара; очень сально сплющенного эллипсоида вращения; трехосного эллипсоида двух различных видов; наконец, она может принимать некоторые цилиндрические и грушевидные формы. Возникающие здесь задачи имеют большую важность для определения фигур небесных тел. Из старых авторов в этой области работали Клеро, Якоби; из новых — Пуанкаре, Джордж Дарвин.

II. Гидродинамика. Гидродинамикой называют учение о движении жидкостей. Основателем гидродинамики можно назвать Торричелли, который, исследуя истечение воды из малого отверстия в сосуде, открыл, что если вытекающей струе дать вертикальное направление, то высота ее почти достигает уровня воды в сосуде. Торричелли допускает, что вода поднялась бы в точности до этого уровня, если бы можно было устранить все сопротивления, и отсюда выводит, что скорость вытекающих частиц воды равняется той скорости, какую получили бы они, падая с высоты уровня воды в сосуде. Этот закон Торричелли выражается формулой v = √2gh, где v — скорость вытекающих частиц, h — вертикальное расстояние между отверстием и свободной поверхностью жидкости, g — ускорение тяжести. Изложение знаменитой «Гидродинамики» Даниила Бернулли (1738) основано на принципе сохранения живых  сил. В этом сочинении выведена, между прочим, следующая весьма важная теорема: если под действием тяжести происходит установившееся течение жидкости, и если мы означим буквой g ускорение силы тяжести, буквой z — высоту рассматриваемой частицы жидкости над некоторым постоянным уровнем, буквой р — гидродинамическое давление в рассматриваемой точке, буквой ρ — плотность жидкости и буквой v — ее скорость, то для определенной «линии тока» (т. е. траектории частиц жидкости) трехчлен gz+р/ρ+v²/2 имеет постоянное значение во всех точках. Отсюда выяснится существенное различие между давлением гидростатическим, которое вполне определяется глубиной, и гидродинамическим, которое зависит еще от скорости: так что если где-нибудь на линии тока скорость течения v велика (вследствие сужения струи), то гидродинамическое давление здесь будет мало. Оно, может даже сделаться отрицательным, например, когда жидкость, текущая по трубе, попадая в суженное место, отстает от стенок; если в этом месте проделаем отверстие, то сюда будет всасываться воздух. На этом основано устройство гидродинамических насосов.  Впоследствии Лагранж усмотрел, что при известных условиях соотношение, аналогичное теореме Бернулли, имеет место не только для определенной линии тока, но сразу для всей жидкости. Этим объясняется, например, следующий опыт: если продувать воздух через трубку мимо висящего поблизости легкого шарика, то он качнется по направлению к выдуваемой струйке, т. е в ту сторону, где гидродинамическое давление меньше.

Методы, помощью которых получал свои выводы Д. Бернулли, страдали недостатком общности и в некоторых случаях оказывались неверными. Строго точные уравнения движения жидкостей в дифференциальной форме были даны в 1752 г. Даламбером, который применил свою общую динамическую теорему к уравнениям равновесия жидкости, выведенным Клеро. Но в самой простой и общей форме дифференциальные уравнения гидростатики были даны гениальным математиком Эйлером. В зависимости от того, интересуемся ли мы состоянием в одной и той же точке пространства, занятого жидкостью, или же следим за состоянием определенной жидкой частицы, уравнения гидростатики пишутся в двух различных формах; второй из этих видов часто называют Лагранжевым. После того как установлены дифференциальные уравнения гидростатики решение всех ее задач (т. о. полное определение обстоятельств движения и действия жидкости, движимой какими-нибудь силами) сводится вообще к интегрированию этих уравнений, применительно к данным частным условиям; но весьма часто такое интегрирование бывает сопряжено с большими трудностями. Из вопросов, которые частью удалось решить, назовем: течение жидкости в двух измерениях (т. е. такое, которое является одинаковым во всех плоскостях, перпендикулярных к некоторому направлению); распространение волн (см.); движение вихрей (см. вихревые движения); движение твердого тела, имеющего полости, наполненные жидкостью; движение твердых тел в жидкости. В направлении последнего вопроса очень интересны исследования норвежского математика Бьеркнеса о пульсирующих телах (см. притяжение).

Упомянутые выше исследования относятся к т. н. «идеальной» жидкости, — которая не обнаруживала бы внутреннего трения (вязкости). Ни для одной действительной жидкости это требование в точности не выполняется; поэтому является надобность дополнить уравнения гидростатики новыми членами, зависящими от вязкости. Это впервые сделал Навье в 1827 г., а затем, в более общей форме, — Сен-Венан в 1843 г.

III. Аэродинамика. Аэродинамикой называется учение о движении газов. Аэродинамика пользуется теми же математическими методами, что и гидродинамика; однако в гидродинамике обыкновенно плотность движущейся жидкости считается неизменной, тогда как в аэродинамике плотность газа считают, согласно закону Мариотта, пропорциональной его упругости. Из задач, решаемых в аэродинамике, особенно важной является задача о движении твердого тела в газообразной среде; находимые здесь результаты имеют широкое применение к артиллерийскому делу и к авиации (см. воздухоплаванье).

IV. Теория притяжения. Известно, что всякие две материальные частицы притягиваются между собой по закону Ньютона f = k(mm¹/r²), где f – сила притяжения, m и m¹ – массы частиц, r – расстояние между ними, k – коэффициент пропорциональности, зависящий только от выбора единиц. Вообразим материальное тело определенной формы; спрашивается, с какой силой и по какому направлению будет оно притягивать материальную частицу, расположенную известным образом по отношению к нему? Спрашивается также, как будут притягиваться между собой два материальные тела (например, два шара, два эллипсоида)? Вот характерные вопросы, решаемые теорией притяжения. При решении подобных задач весьма большую пользу приносит одна математическая функция, называемая потенциалом. Пусть m₁, m₂, m₃ и т. д. будут массы притягивающих частиц; тогда потенциал их в какой-нибудь точке О пространства выражается формулой

k(m₁/r₁ + m₂/r₂ + m₃/r₃ +…), где r₁, r₂, r₃ и т. д. суть расстояния от каждой из наших частиц до точки О. Легко обнаружить, что численное значение потенциала в точке О равно численному значению той энергии или работы, которую выделяет система действующих масс, когда она, притягивая свойственными ей силами массу, равную единице, приводит ее из бесконечно удаленной части пространства в рассматриваемую точку О; оно также равно численному значению той работы, которую должен затратить какой-нибудь внешний агент, когда он, побеждая притяжение системы масс, удаляет единичную массу из точки О в бесконечную даль. (Нередко дают самое определение потенциала в этой форме, и отсюда уже выводят его математическое выражение.) Так как по закону прямой пропорциональности массам и обратной пропорциональности квадрату расстояния протягиваются не только частицы материи, но также электрические заряды и магнитные полюсы, то теория потенциала оказывает существенное содействие также при решении задач из области электричества и магнетизма. Но этого мало: дифференциальные уравнения, к которым приводит теория потенциала, оказываются аналогичными тем, с которыми имеет дело гидродинамика, а также тем, которые служат для изображения процесса распространения теплоты в каком-нибудь теле путем теплопроводности. Благодаря этому, различные задачи теории притяжения материальных, электрических и магнитных масс, а также теории теплопроводности и гидродинамики становятся в соответствие друг с другом; и через посредство теории потенциала механика приводится в близкую связь с  математической физикой.

V. Теория упругости и теория сопротивления материалов. Теория упругости занимается исследованием деформации, которым подвергаются тела под действием внешних сил. Основная задача теории упругости заключается в том, чтобы выразить усилия в деформированной среде в зависимости от характеристических элементов деформации в каждой точке, а затем получить отсюда уравнения равновесия и движения среды под действием данных внешних сил. Наиболее простым является тот случай, когда деформации очень малы; тогда усилие можно считать пропорциональным соответствующей деформации (закон Гука).

Теория упругости, примененная к целям строительства, носит название теории сопротивления материалов. Здесь главной целью является определение внутренних усилий, разливающихся в различных частях какого-нибудь сооружения, причем для прочности его эти усилия не должны превышать установленных предельных значений. Другой задачей является определение форм и размеров сооружения таким образом, чтобы, с одной стороны, была соблюдена возможная экономия в материале, а с другой — чтобы сооружение удовлетворяло условиям прочности.  Начало научного исследования законов упругости было положено в 1638 г. Галилеем, который исследовал прочность бруса, свободно лежащего на двух опорах, и установил, что наибольший груз, поддерживаемый таким брусом, пропорционален его ширине, пропорционален квадрату вышины и обратно пропорционален длине. В XVIII веке вопросом о сопротивлении материалов занималась Эйлер и Лагранж. В 1807 г. Юнг ввел весьма важное понятие о модуле упругости: это — коэффициент, характеризующий в известном смысле упругие свойства вещества и измеряющийся той силой, которая должна действовать на каждую единицу площади основания призматического тела, чтобы длина этой призмы увеличилась вдвое (предполагая, что при этом не перестает соблюдаться закон Гука). Особенное развитие получила теория упругости в XIX в. как в чисто теоретическом направлении (трудами Навье, Пуассона, Коши, Ламе), так и в техническом направлении (работами Навье, Понселе и др.).

VI. Графическая статика. Представим себе сооружение, состоящее из стержней, соединенных между собой (например, стропильную или мостовую ферму); пусть отдельные части этого сооружения находятся как под действием собственного веса, так и под действием различных грузов и других сил, приложенных к ним. Вся эта система сил пусть будет такова, что на твердом теле она уравновешивается. Под действием этой системы сил в стержнях разминаются некоторые напряжения. Основная задача графической статики заключается в том, чтобы определить эти напряжения графическим путем.   Одним из основных понятий в графической статике является т. н. веревочный многоугольник. Пусть мы имеем n точек А₁, А₂, А₃,..., A_n-1, А_n, соединенных нерастяжимыми веревками A₁ А₂, А2 А₃, А₃ А₄..., A_n-1 А_n. К точкам A₁, А₂, А₃,... А_n-1, А_n приложены данные силы Р₁, Р₂, Р₃,.., P_n-1, Р_n, действием которых натягиваются веревки А₁ А₂ и т. д. Такая система веревок, расположенных по ломаной линии, концы которой суть А₁ и А_n, и называется веревочным многоугольником. Если заменить веревки твердыми стержнями, то получится многоугольник плеч. Чтобы узнать, может ли такой многоугольник данными вилами удерживаться в равновесии, и какой вид будет он иметь при этом, строят т. н. силовой многоугольник таким образом. Из  произвольной точки О проводят прямом отрезок (О₁), имеющий величину и направление силы P₁; из конца его I проводят другой отрезок (l₂), равный и параллельный силе Р₃, и т. д. Продолжая это построение, дойдем наконец до отрезка (n-ln₁), равного и параллельного силе Рn. Если конец n этого обрезка совпадет с начальной точкою О, т. е. если силовой многоугольник замкнется, то наша система может находиться в равновесии, а именно в таком положении, что веревка или плечо А₁ А₂ будет параллельна прямой (О₁), А₄ А₃ будет параллельна диагонали (О₂), А₂ А₄ будет параллельна диагонали (О₃) и т. д.; длины же диагоналей будут изображать величины натяжений соответственных веревок или плеч.

VII. Теория механизмов и теория машин. Подобно тому, как статика находит себе непосредственное техническое применение в теории сооружений, так  и другие два отдела общей механики — кинематика и динамика — дают начало двум соответственным отделам прикладной механики — теории механизмов и теории машин (см. машина, механизм).

Литература по общей механике: Бачинский, «Учение о силах и движении», 1914; Кирпичев, «Беседы о механике», 1907; Мах, «М.» (историко-критический очерк ее развития), 1909; Жуковский, курсы механики под различными названиями; Аппел, «Руководство теоретической механики», 3 тома, 1911. См. также библиографию в   Encycl. der mathem. Wissenchaften (Teubner), Band IV.

А. Бачинский.