Многоугольник и многогранник

Многоугольник и многогранник.  Полным плоским n-угольником называется совокупность n точек плоскости, из которых никакие три не лежат на одной прямой, и совокупность n(n-1)/2 прямых, определяемых этими точками. Полным  плоским n-сторонником называется совокупность n прямых на плоскости, из которых никакие три не проходят через одну точку, и совокупность n(n-1)/2  точек пересечения этих прямых. Простым n-угольником называется такая система n отрезков, в которой каждая из конечных точек одного отрезка совпадает с конечной точкой одного и только одного из остальных отрезков. Простой n-угольник тождествен с простым n-сторонником и полный n-угольник содержит n(n-1)/2 простых.  

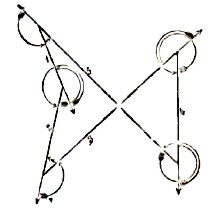
Рис. 1.

Если мы выберем на простом n-угольнике положительное направление обхода всех его сторон (периметра) и будем считать положительным направление вращения против стрелки часов, то угол, на который нужно в положительном направлении повернуть сторону, чтобы она совпала с положительным направлением следующей стороны, называется внешним. Угол, на который нужно в положительном направлении повернуть сторону, чтобы она совпала с отрицательным направлением предыдущей стороны, называется внутренним (черт. 1). Если все внутренние углы меньше π, то многоугольник называется выпуклым. Сумма внешних углов равна 2аπ (1≤а≤n-1); число а называется родом многоугольника. Многоугольник, в котором все стороны и углы между собой равны, называется правильным; каков бы ни был  его род, около него всегда можно описать и в него вписать окружность.

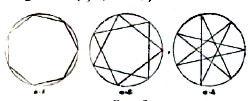
Рис. 2.

Если α, β, … суть различные первоначальные множители числа n, то существует всего N = n/2(1-1/α)(1-1/β)… правильных n-угольников.

Так, существует всего три правильных 7-угольнпка первого, второго и третьего родов (черт. 2). Правильные многоугольнике первого рода изучаются в элементарной геометрии.

Полным телесным n-угольником называется совокупность n точек, из которых никакие четыре не лежат в одной плоскости, прямых, соединяющих эти точки попарно, и плоскостей, проходящих через каждые три из этих n точек. Полный n-гранник состоит из n плоскостей, из которых никакие четыре вообще не проходят через одну точку, и из прямых и точек пересечения этих плоскостей. Простым n-гранником называется совокупность n плоских n-угольников, у которых все стороны каждого совпадают с сторонами некоторых из остальных n-угольников.

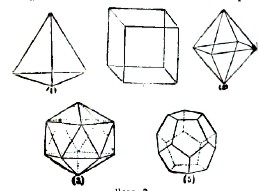
Рис. 3.

Совокупность этих многоугольников образует связную поверхность многогранника. Если мы обозначим через Е, К, Р число телесных углов, ребер и граней односвязного двухстороннего многогранника, то Е — К + F = 2 (закон Эйлера). В случае n-связного многогранника имеем Е — К + F = 3 — n. Коши доказал, что всякий выпуклый эйлеров многогранник вполне определяется его поверхностной сетью. Многогранник называется правильным, если все его грани суть конгруэнтные правильные многоугольники и все его телесные углы также правильны и конгруэнтны. Возможны только пять правильных многогранников: 1) тетраэдр, 2) октаэдр, 3) икосаэдр, 4) гексаэдр, 5) додекаэдр (черт. 3). Литература предмета очень обширна; укажем: Max Brückner, «Viеlecke und Vielflache, Theorie und Geschichte» (1900).

А. Некрасов.