Небесная механика

Небесная механика. Небесная сфера. Орбита.

1. Небесная механика есть отдел астрономии, в котором исследуется на основании принципов и теорем механики движение небесных тел под действием сил, влияющих на их движение, прежде всего, главным образом и часто исключительно под действием сил взаимного притяжения их по закону Ньютона.

1. Ньютон показал (см. планеты), что законы движения планет, эмпирически найденные Кеплером, объясняются механически, если предположить, что Солнце притягивает каждую планету с силой, величина которой зависит от расстояния между Солнцем и планетой и уменьшается пропорционально квадрату этого расстояния. Исходя из этого, Ньютон точнее формулировал закон взаимного притяжения, а именно, что каждая частица вещества в солнечной системе притягивает каждую другую частицу с силой, изменяющейся обратно пропорционально квадрату расстояния между ними и пропорционально количеству вещества в каждой частице, или пропорционально массе каждой частицы. Поэтому при рассмотрении взаимного притяжения двух каких-либо тел мы должны вообразить себе, что каждая частица одного из них притягивает по указанному закону каждую частицу другого; все эти силы — малые, так как объем, а следовательно, и массу каждой частицы мы воображаем сколь угодно малыми, но по правилам механики все эти силы можно сложить и заменить их все одной равнодействующей; подробное расследование показывает, что эта равнодействующая в общем случае не проходит чрез центр тяжести тела, но ее можно заменить совокупностью 1) силы, приложенной в центре тяжести тела, которая стремится изменить движение центра тяжести, и 2) пары сил, стремящейся изменить вращение тела около его центра тяжести. Таков же результат получается и в том случае, когда имеется не два, а несколько взаимно притягивающихся тел; в результате действия каждой частицы всех прочих тел на каждую частицу одного из них получается сила, приложенная к его центру тяжести, и пара сил, вращающая тело около этой точки. Таким образом наследование движений небесных тел под действием их взаимного притяжения приводится к двум независимым задачам: 1) задача о движении центров тяжести небесных тел; центр тяжести каждого тела движется так, как будто бы в нем было сосредоточено все вещество, вся масса тела; он является в этом случае тем, что называется материальной точкой; 2) задача о вращении тела около его центра тяжести; это вращение происходит независимо от движения центра тяжести, как будто бы он был неподвижен.

2. Если тела имеют сферическую форму и каждое — равномерную плотность во всем объеме, или если слои одинаковой плотности имеют сферическую форму, то равнодействующая взаимных притяжений частиц сводится только к одной силе, без пары сил, и величина этой силы в точности обратно пропорциональна квадрату расстояния между центрами тяжести и пропорциональна произведению масс обоих взаимно тяготеющих тел; вообще говоря, это условие в природе точно никогда не осуществляется, но существенно важно для небесной механики, что, если размеры тел малы сравнительно с расстоянием между ними, то величину равнодействующей, приложенной в центре тяжести каждого из них, с очень большой точностью можно все-таки считать обратно пропорциональной квадрату расстояния между центрами тяжести, и допускаемая при этом неточность тем меньше, чем меньше размеры тел сравнительно с их расстоянием друг от друга; пара сил при этом не исчезает, но ее момент также тем меньше, чем меньше размеры тел сравнительно с их расстоянием (он уменьшается приблизительно пропорционально кубу этого расстояния); таковы именно условия взаимного притяжения Солнца и планет. Более того, не только размеры планет очень малы сравнительно с их расстояниями, но даже и размеры орбит их спутников также достаточно малы, поэтому равнодействующие сил взаимного притяжения между этими системами (планета + ее спутники) с достаточной точностью могут считаться обратно пропорциональными квадратам расстояний между центрами тяжести этих систем. Поэтому, например, движение Земли относительно Солнца разлагается на две задачи: 1) движение общего центра тяжести Земли и Луны относительно Солнца в 2) движение Земли относительно этого центра тяжести.

3. На основании законов динамики доказывается, что если сила, притягивающая материальную точку по направлению к неподвижной топке (т. н. центр притяжения), изменяется обратно пропорционально квадрату расстояния между материальной точкой и центром притяжения, то материальная точка описывает коническое сечение (эллипс, параболу или гиперболу), в одном из фокусов которого находится центр притяжения, причем радиус-вектор материальной точки описывает площади, пропорциональные времени (иными словами, площадь, описываемая радиусом-вектором в единицу времени, одинакова во всех частях орбиты; или: скорость материальной точки в каждой точке орбиты обратно пропорциональна длине перпендикуляра, опущенного из центра притяжения на касательную к орбите в этой точке). Если неподвижного центра притяжения нет, а есть две материальные точки с массами m₁, m₂, взаимно притягивающие друг друга с силой ньютоновского притяжения (сила   F = k²(m₁m₂)/r², где r — расстояние между m₁ и m₂, а  k² — коэффициент, величина которого зависит от принятых единиц длины, массы и времени), то общий центр тяжести этих материальных точек либо неподвижен, либо движется прямолинейно и равномерно, а каждая точка движется вокруг него по коническому сечению, как около неподвижного центра притяжения; оба эти конические сечения одинаковы по форме (т. е. у них одинаковый эксцентриситет), размеры же их обратно пропорциональны массам материальных точек: большая масса  описывает меньшую орбиту, меньшая — большую. Из этого можно вывести, что движение любой массы, например, m₁, относительно другой m₂ таково, что m₁ описывает относительно m₂ коническое сечение той же самой формы, как пути их относительно общего центра тяжести, и с тем же законом движения, так что движение каждой из них относительно другой таково, как будто бы последняя была неподвижным центром притяжения. При этом, если коническое сечение есть эллипс, то в течение некоторого времени одна точка совершает полный обход по эллипсу вокруг другой, это есть время обращения Т; если обозначить через а половину большой оси эллипса (она же есть среднее расстояние между m₁ и m₂, то можно доказать, что величина T²(m₁+m₂)/a³ есть величина постоянная во всех случаях, она равна 4π²/k² где π – отношение длины окружности к диаметру, а k вышеупомянутый коэффициент; следовательно, величины Т, а и (m₁+m₂) не могут быть произвольными; если известны две из них, то третью можно вычислить. Сообразно со всем изложенным, если есть два небесные тела, частицы которых взаимно притягиваются по закону Ньютона, а размеры их достаточно малы сравнительно с их расстоянием друг от друга, то центры тяжести их движутся вокруг общего центра тяжести по указанным законам; мы не можем видеть этого движения, так как общий центр тяжести не видим, мы наблюдаем лишь движение геометрического центра одного тела относительно другого, но, как указано, это относительное движение подчиняется тем же законам; эти законы выражают собой все свойства движений в этой задаче, т. н. задач о двух телах.

4. Задача о трех телах, т. е. о движении трех материальных точек, взаимно притягивающих друг друга по закону Ньютона, в общем виде, т. е. при любых массах, при любом расположении тел и любых скоростях в какой-либо момент движения, не решена до сих пор, т. е. не получено ни каких-либо общих законов движения каждого тела в отдельности, ни полной формулы, по которой можно было бы вычислить положение каждого тела в любой момент времени. Однако, хотя такого общего и точного решения задачи о трех и о многих телах и не получено, астрономы могут вычислять с достаточною точностью движения тел в солнечной системе, но это возможно лишь потому, что 1) масса Солнца, а потому и его притягательная сила, гораздо больше массы и притягательной силы каждой планеты (см. таблицу масс при ст. планеты), и 2) ни одна из больших планет не подходит очень близко ни к Солнцу, ни к другой большой планете. Вследствие этого движение каждой планеты главным образом зависит от взаимного притяжения между нею и Солнцем, другие планеты своим притяжением лишь немного видоизменяют (возмущают, как говорится) эллиптическое (невозмущенное) движение планеты относительно Солнца, которое было бы, если бы другие планеты не существовали.

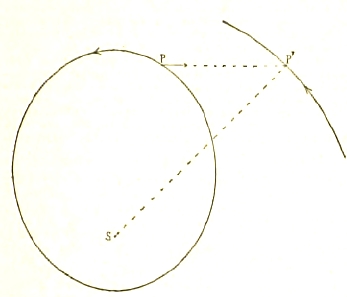
Пусть (см. рис.) S — Солнце, Р — планета, которая при отсутствии других планет описывала бы относительно Солнца эллипс, означенный на рисунке; в каждый момент она имеет некоторую скорость, определенную по величине и по направлению ее; величина и направление ее непрерывно, без скачков, меняются вследствие взаимного притяжения Солнца и планеты. Вообразим теперь, что существует еще другая планета Р', движущаяся по какой-либо орбите. Она своим притяжением видоизменяет движение планеты Р относительно S, и притом изменение это, так сказать, двухстороннее: во-первых, она притягивает к себе планету Р' по закону Ньютона и этим непрерывно изменяет величину и направление ее скорости, но, кроме того, планета Р' притягивая к себе Солнце, заставляет и его перемещаться немного иначе, чем оно двигалось бы в отсутствии ее (вокруг общего центра тяжести Солнца и планеты Р); можно сказать, что планета Р', кроме непосредственного действия на планету Р, еще меняет место того фокуса (центр Солнца), относительно которого планета Р должна описывать эллипс. Если, как это и есть на деле в солнечной системе, масса планеты Р' мала сравнительно с массой Солнца, то оба указанные влияния планеты Р' на движение планеты Р относительно Солнца изменяют величину скорости Р относительно S лишь на очень малую долю ее и направление скорости лишь на очень малый угол; поэтому и возмущенное планетой Р' движение планеты Р относительно Солнца лишь немного отклоняется от невозмущенного. Эти отклонения (т. н. возмущения) можно вычислить с достаточно большой, для целей естествознания, точностью именно потому, что они невелики; если бы среди планет была хоть одна, масса которой не очень много разлилась бы от массы Солнца, то движение остальных планет было бы гораздо сложнее, чем оно есть нa деле, и вычисление их движений было бы несравненно труднее, чем при настоящих условиях в солнечной системе. Существенно при этом, что степень точности, которая может быть достигнута и достигается при вычислении возмущений, вполне соответствует точности даже теперешних наблюдений, так что, сопоставляя результаты вычислений с наблюдениями, астрономы могут судить о том, действительно ли движение планет управляется лишь притяжением Солнца и их взаимными притяжениями, или к этому присоединяются еще какие-либо силы природы, а также и о том, точно ли взаимное притяжение выражается законом Ньютона (обратно пропорционально квадрату расстояния); ср. сказанное в ст. Планеты и Луна. Отклонения движения планет от эллиптического движения, или т. н. возмущения, разделяются на 1) периодические и 2) вековые. Первые таковы, что они изменяют движение небесного тела то в одну, то в другую сторону, например, то ускоряют его, то замедляют; периоды этих колебаний могут быть в разных случаях весьма разнообразны: от немногих недель до нескольких десятилетий или столетий. Вековыми возмущениями называются такие, которые изменяют движение в одну и ту же сторону, например, все время ускоряют его; некоторые из этих возмущений суть, говоря строго, тоже периодические, но с огромными периодами в несколько тысячелетий, так что в течение нескольких сотен лет изменение движения сохраняет один и тот же характер.

5. Если расстояние между взаимно тяготеющими телами не очень велико сравнительно с размерами хоть одного из них, то форма их оказывает уже заметное влияние на величину равнодействующей взаимного притяжения их частиц; если, как, например, в случае планет, тело более или менее сплюснуто, то вследствие этой сплюснутости сила притяжения между телами, например, между планетой и ее спутником, меняется уже по более сложному закону, чем квадрат расстояния между их центрами тяжести, и от  этого движение получается не эллиптическим, а более сложным. Эти обстоятельство учитывается при исследовании движения спутников вокруг их планет. Кроме того, на движение каждого спутника влияет еще притяжение других спутников той же планеты, а главным образом притяжение Солнца, опять таки вследствие его большой массы. Это влияние зависит от  различия влияния Солнца на движение планеты и на движение ее спутника; притяжение Солнца в каждый момент изменяет скорость планеты и скорость спутника, но не одинаково, потому что и их расстояния от центра Солнца, вообще говоря, не одинаковы, и направления от их центров к центру Солнца не совпадают; различие этих непрерывных изменений скорости и ее направления у планеты и у спутника вносит непрерывное изменение в то движение спутника относительно планеты, которое было бы при отсутствии Солнца. Чем дальше отстоит спутник от планеты, тем больше это влияние Солнца на его движение вокруг планеты; с другой стороны, чем дальше планета со спутником от Солнца, тем меньше возмущающее действие Солнца на движение спутника; оно уменьшается пропорционально кубу расстояния; так что, например, возмущающее действие Солнца на движение спутника Нептуна вокруг Нептуна приблизительно в 27 000 раз меньше возмущающего действия его на движение луны вокруг Земли (Нептун дальше Земли от  Солнца приблизительно в 30 раз, а его спутник находится приблизительно на таком   же расстоянии от него, как Луна от Земли). В случае Луны и Земли возмущающая сила Солнца может достигать 1/75-й доли взаимного притяжения между Землей и Луной; она значительно больше той возмущающей силы, которая происходит от сплюснутости Земли. Подобно Солнцу, на движение спутников вокруг планеты действуют и прочие планеты, но по малости их масс их действие очень мало сравнительно с действием Солнца.

6. Из предыдущего ясно, что при практическом применении общих теорем и формул небесной механики к исследованию движений планет, их спутников, комет нужно знать их массы и, для начала хоть приблизительно, их пути относительно Солнца, чтобы можно было для каждого момента вычислить возмущающее действие любого небесного тела на каждое из остальных. Конические сечения, приближенно представляющие действительные пути планет и комет относительно Солнца, выводятся из видимых движений их на фоне звездного неба; массы же проще и точнее всего получаются для тех планет, у которых есть спутники, и именно из движений спутников вокруг планет. Из вышеприведенной (см. § 3) формулы  T²(m₁+m₂)/a³ = 4π²/k² следует, что величина отношения пропорциональна сумме взаимно тяготеющих масс m₁ и m₂ исходя из этого, можно определить отношение масс различных планет и Солнца. Например, Земля с Луной движутся вокруг Солнца на расстоянии, которое приблизительно в 389 раз больше среднего расстояния от Земли до Луны, и время обращения Земли с Луной вокруг Солнца приблизительно 365 дней, а Луны вокруг Земли 27,3 дней: отсюда: масса (Солнце + Земля + Луна) больше массы (Земля + Луна) в 389³/365² : 1/27,3², т. е. в 329000 раз; значит, масса (Земля + Луна) значительно меньше массы Солнца, и мы можем принять, что масса Солнца в 329 тыс. раз больше массы (Земля + Луна). Из других, более сложных явлений в соображении (которых по их сложности мы здесь не касаемся) можно определить, что масса Земли приблизительно в 80 раз больше массы Луны; значит, масса Солнца приблизительно в 333 тыс. раз больше массы одной Земли. Подобным же образом для каждой планеты, имеющей спутника, можно вычислить, во сколько раз ее масса меньше массы Солнца. Массы планет, у которых спутников не найдено (Меркурий и Венера) можно определить только гораздо более сложным путем, а именно, на основании учета тех возмущений, которые они оказывают на движение либо других планет, либо комет, в особенности тех комет, которые проходят недалеко от них; например, масса Меркурия определяется в исследование движения кометы Энке, которая заходит внутрь орбиты Меркурия и иногда проходит близко от него. Массы малых планет и комет так малы, что притяжение, оказываемое ими на другие небесные тела, до сих пор не обнаружено наблюдениями.

7. Как указано ранее, равнодействующая притяжений, которые оказывают частицы одного тела на частицы другого, вообще говоря, не проходит через центр тяжести последнего тела, и потому ее действие равносильно совокупному действию такой же по величине и направлению силы, приложенной в центре тяжести, и действию некоторой пары сил. Эта пара сил влияет на характер вращения тела (предполагаемого абсолютно твердым) около его центра тяжести, непрерывно изменяя направление оси вращения в скорость вращения. В астрономии это обстоятельство имеет особенно важное значение применительно к Земле, с которой мы наблюдаем все движения во вселенной, и движение которой самой мы должны знать возможно точнее, чтоб принять его во внимание при исследовании движения других небесных тел. Вследствие того, что Земля не точный шар, а имеет форму сфероида, равнодействующая сил притяжения какого-либо внешнего тела не проходит через ее центр тяжести, и поэтому возникает пара сил, стремящаяся изменить ее вращение. Заметное влияние при этом оказывают лишь Солнце и Луна; массы планет слишком малы, а расстояния их от  Земли слишком велики, чтоб их влияние могло быть заметным; действие Луны, несмотря па ее малую массу, вдвое с лишком превосходит действие Солнца, именно потому, что она значительно ближе к Земле, чем Солнце. В каждый момент времени пара сил, получающаяся, например, от Луны, стремится повернуть земной сфероид около того диаметра его экватора, который в этот момент перпендикулярен к линии, соединяющей центр Земли с центром Луны, и в такую сторону, чтоб земной экватор совпал с плоскостью орбиты Луны; но по теореме механики, по причине вращения Земли около оси никакого поворота около этого диаметра не происходит, а напротив, ось вращения Земли стремится совпасть с указанным диаметром экватора, и таким образом возникает принужденное перемещений земной оси в пространстве;  подобным же образом действует и Солнце; в результате получается то движение земной оси в пространстве, которое известно под именем прецессии и нутации (см.). По существу дела такое движете оси вращения Земли, возникающее от того, что внешняя сила стремится повернуть Землю около диаметра ее экватора, совершенно аналогично с движением т. н. гироскопа (волчок в оправе), подвешенного на нитке за верхний конец так, что ось вращения его не вертикальна; если волчок вертится, то эта ось описывает конус около вертикальной линии вследствие того, что сила тяжести стремится повернуть волчок около горизонтальной линии; в обыкновенном волчке, без оправы, опирающемся на стол, движение с внешней стороны похоже, но динамически сложнее. В небесной механике выводятся точные формулы, устанавливающие скорость движения земной оси и ее положение в пространстве в любой момент времени в зависимости от видимого движения Лупы и Солнца.

8. При рассмотрении вышеуказанных вопросов небесные тела рассматриваются как абсолютно твердые; в действительности этого не бывает; все тела более или менее сжимаемы, некоторые находятся хотя отчасти в капельно-жидком состоянии, либо в газообразном; кроме того, те из них, которые теперь, можно думать, отвердели или, по крайней мере, покрылись корой, когда-то были в капельно-жидком или газообразном состоянии. Эти соображения вызывают ряд задач небесной механики, вообще говоря, более сложных и трудных для исследования, чем вышеуказанные. Таковы вопросы о форме небесных тел, которая зависит от условий их образования, их вращения и действия на них других близких тел; о движении двух тел, находящихся в жидком или газообразном состоянии вокруг общего центра тяжести; о движении жидких масс на поверхности более или менее твердого тела (приливы и отливы на Земле); вопросы космогонического характера: о переходе небесных тел из одного состояния в другое, о движении их при иных условиях, чем те, при которых мы их теперь наблюдаем; вопросы о роли в мироздании иных сил, кроме силы взаимного притяжения по закону Ньютона, и т. п. вопросы.  Для подробного ознакомления с методами и результатами исследований в небесной механике необходимо основательное знание высшей математики и механики. Основным руководством в настоящее время служит: F. Tisserand, «Traité de méсanique céleste», 4 т.; краткий курс для общего ознакомления с небесной механикой: F. Moulton, «Аn introduction to celestial mechanics».

Небесная сфера есть воображаемая сферическая поверхность произвольного радиуса, служащая для удобного рассмотрения различных вопросов астрономии, относящихся к видимому расположению небесных светил и изменению этого расположения от различных причин. Непосредственное наблюдение простым ли глазом или с помощью астрономической трубы дает нам только направление, по которому мы видим в  момент наблюдения то или иное небесное светило: звезду, центр Солнца, ядро кометы и т. п.; мы не можем непосредственно видеть, ни даже судить, как далеко оно от населения. Представим себе наблюдателя где-нибудь на земной поверхности, вообразим себе прямые линии, по которым он видит различные небесные светила, сферу, центр которой в глазу наблюдателя, и точки пересечения этих прямых с поверхностью сферы, тогда ясно, что, каков бы ни был радиус сферы, видимое расположение этих точек при рассматривании сферы из ее центра таково, как видимое расположение небесных светил для указанного наблюдателя; мы можем даже вообразить центр сферы где угодно, вообразить через него прямые, параллельные тем направлениям, по которым наблюдатель видит небесные светила, и точки пересечения сферы с этими прямыми; расположение этих точек будет одинаково с предыдущим; мы можем условно изобразить эту сферу на бумаге, моделировать ее в виде глобуса и по расположению на ней точек  изучать видимое расположение небесных светил для указанного наблюдателя: мы можем самого наблюдателя воображать где угодно, например, в центре Земли, в центре Солнца и т. д., и тогда мы получим т. н. геоцентрическое, гелиоцентрическое и т. д. видимое расположение светил в тот или другой момент времени. Смысл введения небесной сферы заключается в том, что удобнее, наглядно исследовать взаимное расположение точек на ней, чем взаимное расположение прямых линий, исходящих из ее центра; такая сфера является для нас подобием той сферической поверхности, которую наблюдатель намеренно или невольно воображает вокруг себя и на которой он воображает расположенными наблюдаемые им небесные светила, представляя себе радиус ее громадным в сравнении с размерами либо глаза, либо астрономического инструмента, либо Земли, либо солнечной системы, хотя нет надобности воображать этот радиус бесконечно большим;  для вполне ясного понимания дела необходимо всегда представлять себе и точки на небесной сфере и соответствующие направления из ее центра. Видимые движения небесных светил мы представляем как движения соответственных точек на небесной сфере, и из них уже теоретическим путем астрономы выводят действительное расположение небесных тел в пространстве и их действительные движения; и обратно, для проверки астрономических теорий необходимо из вычисленного расположения в какой-либо момент небесных светил в пространстве вывести их видимые положения в тот же момент, т. е. положения соответственных точек на небесной сфере. Для этих целей нужно 1) условиться, как определять на небесной сфере положение каждой точки, 2) исследовать от каких причин и как именно меняется видимое расположение светил независимо от действительного движения их  в небесном пространстве. Эти вопросы составляют содержание основ т. н. сферической астрономии.

Положение точки на сфере определяется при помощи особых координат, т. н. сферических; в астрономии употребляются различные системы их; в основе каждой лежит некоторая определенная линия и перпендикулярная к ней плоскость, по имени которой называется и сама система координат.

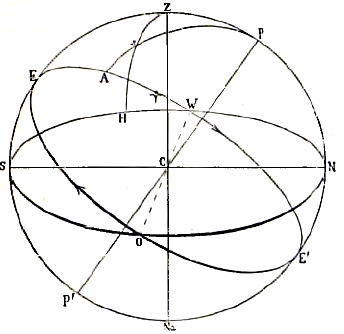
Рис. 1.

Вообразим (см. рис. 1) в какой-нибудь точке С на земной поверхности небесную сферу и отвесную, или вертикальную линию, т. е. параллельную направлению силы земной тяжести; она встречает небесную сферу в точках Z и Na; положим, направление от С к Z есть направление от поверхности Земли вверх; тогда Z называется зенит, Na — надир, перпендикулярная к CZ, т. н. горизонтальная плоскость, проходящая через С, пересекает небесную сферу по большому кругу N OS W (т. н. горизонт); половина небесной сферы кверху от горизонта доступна непосредственному наблюдению из точки С, нижняя половина небесной сферы закрыта телом Земли, предполагая, что С находится на море или в степи, где высокие предметы не загораживают части небесной сферы у горизонта и не закрывают находящиеся здесь небесные светила. Вообразим прямую РСР’, параллельную оси вращения земли, Р и Р’ суть точки пересечения ее с небесной сферой; это (см. Земля) суть полюсы мира; пусть Р есть тот из них, который лежит в созвездии Малой Медведицы, то есть так называемый северный полюс; мы выбрали для рисунка место на Земле так, чтобы Z было ближе к Р, чем к Р’, следовательно, это место С лежит в северном полушарии Земли; если бы взять диаметрально противоположную точку на Земле (например, вместо северного конца Байкальского озера западный конец Огненной земли), то на чертеже нужно было бы переместить Z и Na. Вообразим плоскость, проходящую через С и перпендикулярную к РР'; она пересекает небесную сферу по большому кругу OЕWE’, которая называется экватор; он и горизонт взаимно делятся пополам, пересекаясь в точках О и W. Большой круг небесной сферы, проходящий через Z и Р (а следовательно, и Р‘) называется  меридиан, плоскость его пересекает земной сфероид по земному меридиану точки С; меридиан пересекается с горизонтом в точках N (ближе к Р) и S (ближе к Р'); с экватором — в точках Е (ближе к Z) и Е' (ближе к Na). Наблюдателям на Земле, вследствие вращения Земли, кажется, будто вся вселенная, или небесная сфера, которая ее условно представляет, вращается, как глобус, около оси РР’, так что светила, близкие к Р, описывают круги вокруг Р по направлению против часовой стрелки, а близкие к Р' — вокруг Р’ по направлению часовой стрелки; направление этого кажущегося суточного вращения небесной сферы показано на рисунке стрелкой на экваторе. Вследствие этого вращения небесной сферы светила восходят над горизонтом на его половине NOS и заходят под горизонт на другой половине SWN; точки N, О, S, W, делящие круг горизонта па 4 равные части, называются точками севера, востока, юга, запада; на рис. половина небесной сферы на восток от меридиана обращена к   читателю; на ней все круги проведены более толстыми линиями. Прохождение светила через меридиан называется кульминацией его; если оно пересекает меридиан между Р и S, то это — верхняя кульминация, если между Р и N — нижняя. Горизонт с точкой S на нем составляет основу одной системы координат — горизонтальной. Пусть s — какая-нибудь точка на небесной сфере (Cs — направление от наблюдателя к соответствующему светилу); вообразим большой круг через Z и s, пересекающий горизонт в точке Н; он называется кругом высоты; sН есть высота h точки s, u Zs — ее зенитное расстояние z; дуга ZН равна 90°; следовательно, всегда s + h = 90; дуга круга горизонта SH = а, считаемая от точки юга до круга высоты по направлению на запад, север, восток от 0° до 360°, называется азимутом; очевидно, если известен азимут а, то известно положение точки Н и круга высоты, а если, кроме того, известно s или h , то вполне определенно и точно известно положение точки s на небесной сфере; азимут и высота (или, вместо высоты, зенитное расстояние) суть координаты точки s в этой системе координат. Иногда азимут считается от S в обе стороны, к 0 и к W, от 0° до 180°; иногда, например, в мореплавании при отсчетах компаса, азимуты, румбы, считаются и от S, и от N, и к О и к W, например, N45°W. Дуга ZP, зенитное расстояние полюса, и PN, высота полюса над горизонтом, зависят от положения места С на земной поверхности (см. Земля); PN = географической широте φ места С; ZP=90°—φ. В другой, экваториальной, системе координат основная плоскость есть экватор с точкой Е на нем, лежащей в меридиане над горизонтом, в верхней кульминации (нижняя кульминация точки на экваторе приходится под горизонтом, точка Е'); вообразим дугу большого круга небесной сферы через P и s, пересекающую экватор в точке А; дуга Ps называется полярным расстоянием р точки s, дуга sА —ее склонением δ; р считается от северного полюса Р от 0° до 180°, δ считается от экватора к Р и тогда называется северным (положительным) склонением (+δ) и к Р' и тогда называется южным (отрицательным, —δ); принимая во внимание знак при δ, всегда имеем: р + δ = 90°; круг PsA называется кругом склонения точки s. Дуга экватора ЕА, считаемая от Е до круга склонения по направлению к W, Е', О от 0° до 360°, называется часовым углом t; обыкновенно он выражается в часах, минутах и секундах, считая 360° за 24 часа; так что, например, t = 65°5'0” = 4 ч. 20 мин. 20 сек. Очевидно, часовой угол и склонение (или, вместо него, полярное расстояние) вполне однозначно определяют положение точки s на небесной сфере, подобно а и h, если дано положение полюса и зенита. Поэтому, если, например, известны φ, δ и t, то можно вычислить а и h. Именно, применяя к сферическому треугольнику PZs три осиовыые формулы сферической тригонометрии, получаем:

Отсюда по φ, δ, t вычисляются h и а; это пример т. н. формул для преобразования координат. Если для того же самого момента времени вообразим себе горизонт и зенит другого места С' на земной поверхности, то точка Z переместится на небесной сфере, и от этого все координаты, кроме δ (п р), для места С' будут иными, чем для места С. При этом, если C’ лежит на том же земном меридиане, как и С, то и небесный меридиан у них общий, а потому остаются одинаковыми и δ и t, но φ разное, а потому различим h и а; если же земные меридианы С и С' различны, то часовые углы небесного светила в один и тот же момент времени разнятся па разность географических долгот этих мест; если С' лежит к востоку от С на λ (градусов или часов), то для него часовой угол t’ светила = t + λ; а если к западу, то t’ =  t — λ.

Чтоб определять положение любой точки s на небесной сфере независимо от какого бы то ни было места на земной поверхности, т. е. независимо от меридиана, введена некоторая точка на экваторе, обычно обозначаемая знаком   (знак Овна); это есть точка пересечения экватора и эклиптики, т. е. того большого круга небесной сферы, вдоль которого совершается видимое годичное движение центра Солнца, и именно та точка, где центр Солнца пересекает экватор, переходя из южного полушария неба в северное, что бывает при начале весны в северном полушарии Земли; от этого эта точка и называется точкой весеннего равноденствия; видимое годичное движение Солнца вдоль эклиптики совершается по направлению обратному видимому суточному вращению небесной сферы, т. е. против стрелки на рисунке.^*) Дуга экватора от точки весеннего равноденствия до круга склонения светила, т. е. на рисунке до точки А, называется прямым восхождением его, считается в направлении обратном суточному вращению небесной сферы от 0° до 360°, чаще выражается в часах, подобно часовому узлу, и обыкновенно обозначается буквой α. Промежуток времени между двумя последовательными верхними (или нижними) кульминациями точки весеннего равноденствия есть основная единица времени, — звездные сутки, за начало которых в каждом месте земли принимается момент верхней кульминации точки весеннего равноденствия; дуга экватора Е , т. е. часовой угол точки весеннего равноденствия, будучи выражена в часах (15° на 1 час), показывает, сколько часов звездного времени прошло после начала звездных суток; это есть звездное время в рассматриваемый момент; обозначим его θ: тогда ясно, что θ = α + t и, где α и t относятся к любому светилу. Когда светило находится в верхней кульминации, то t = о и θ = α, т. е. звездное время = прямому восхождению светила, находящегося в верхней кульминации. Заметим еще, что географическая широта φ и звездное время θ могут быть рассматриваемы как склонение в прямое восхождение зенита, это вполне согласуется с определением понятий: склонение прямого восхождения (см. рисунок); φ в каждом месте Земли постоянно, θ — конечно, непрерывно меняется. Вследствие годичного движения Солнца вдоль эклиптики его прямое восхождение увеличивается за сутки приблизительно на 1°; небесная сфера поворачивается на 1° за 4 минуты, следовательно, промежуток времени между двумя последовательными верхними кульминациями Солнца приблизительно на 4 минуты дольше звездных суток; но эти истинные солнечные сутки не постоянны по продолжительности, потому что прямое восхождение Солнца возрастает неравномерно с течением времени 1) вследствие неравномерности углового движения Солнца вдоль эклиптики, 2) вследствие наклонения эклиптики к экватору; поэтому для счета времени по Солнцу введено воображаемое солнце, движущееся равномерно по экватору со средней угловой скоростью действительного Солнца вдоль эклиптики; кульминации этого экваториального солнца то упреждают кульминации действительного Солнца, то запаздывают против них; разница между этими кульминациями (т. н. уравнение времени) может доходить до ¼  часа; промежуток времени между двумя последовательными верхними кульминациями экваториального солнца есть т. н. средние солнечные сутки; этот промежуток делится на 24 час. среднего времени, постоянен и равен 24 ч. 3 мин. 56,555 сек. звездного времени; обратно, 24 ч. звездного времени =23 ч. 56 мин. 4,091 сек. среднего времени. Часовой угол экваториального солнца есть т. н. среднее время в рассматриваемый момент; это — то время, по которому мы все живем и которое признаны показывать наши часы; момент верхней кульминации экваториального солнца есть средний полдень, в этот момент верные часы должны показывать ровно 12 ч. 0 мин. 0 сек., а астрономические часы 0 h. 0 m. 0 s., потому что астрономы считают часы от 0 h. до 24 h., и средние сутки (и числа месяца) у них начинаются со среднего полудня.

^*)  Строго говоря, движение центра Солнца на небесной сфере, рассматриваемое из центра Земли, совершается не по большому кругу, а по очень сложной кривой, вьющейся около некоторого большого круга, но отклонения от него центра Солнца малы и редко превышают 1”; этот большой круг, но очень просто определяемый по видимому движению центра Солнца, и есть эклиптика; поэтому, если желать быть вполне точным, нельзя говорить, что центр Солнца движется по эклиптике; но ввиду сложности определения понятия «эклиптика» этим неточным выражением часто пользуются; чтобы оттенить эту неточность, в тексте принято несколько неопределенное выражение: вдоль эклиптики.

 

Положим, что в рассматриваемый момент времени часовой угол точки весеннего равноденствия, т. е. звездное время в этот момент, есть θ (в градусах или, делением на 15, часах, мин. и сек. звездного времени), что часовой угол среднего солнца, т. е. среднее время в этот же момент есть Т (в градусах или часах, мин., сек. среднего времени); тогда, по общему правилу, θ — Т есть прямое восхождение М среднего экваториального солнца в этот же момент; если оно известно, то, зная Т, можно вычислить θ (θ=Т+М), и обратно, если дано θ, то можно вычислить Т; в астрономических календарях М дается для каждого среднего Гринвичского полдня под названием, понятным на основании предыдущего, «звездного времени в средний Гринвичский полдень»; оно меняется пропорционально времени на 3 мин. 56,555 сек. за 1 средние сутки; поэтому его можно вычислить и для любого момента по любому местному времени; нужно только уметь перевести местное время в гринвичское, т. е. надо знать географическую долготу места от Гринвича. От суточного вращения небесной сферы около оси РР' из координат любой точки а меняются h и а, но не α и δ (однако α и δ могут меняться с течением времени от других причин); но зная α и δ (место светила на небесной сфере), а также φ и θ (место зенита на небесной сфере) в рассматриваемый момент времени, имеем t = θ — α, а зная φ, δ, t, по выше приведенным формулам можно вычислить h (или s) и α. Эти формулы позволяют решать всякие вопросы, относящиеся к суточному вращению неба; например, для определения моментов восхода и заката какого-либо светила нужно лишь обратить внимание на то, что в эти моменты h=0, или z = 90°; поэтому первая из указанных выше формул дает: О = sin φ sin δ + cos φ cos δ cos t, откуда cos t = — tgφ tgδ; если φ и δ даны, вычисляем t (т. н. полудневная дуга), и если к тому же известно α, то имеем θ_в = α — t, звездное время восхода, и θ_з = α + t, звездное время заката; из θ_в и θ_з можно вычислить и соответствующие часы и минуты среднего времени; здесь предположено, что α и δ в оба момента одни и те же; это допустимо только для звезд, у которых α и δ меняются очень медленно; для Солнца же, Луны и планет нужно брать из астрономических календарей α и δ, соответствующие тому моменту восхода или заката, который вычисляют. Рефракция и параллакс влияют на моменты видимого восхода и заката, т. к. от рефракция восхода происходит раньше, а закат позже, чем было бы без рефракции; параллакс же влияет обратно рефракции; не останавливаясь на выводе формулы, укажем лишь, что для учета влияния рефракции и параллакса нужно к углу t, вычисленному из формулы cos t = -tgφ tgδ, прибавить величину (35’-π)/(cos φ cos δ sin t), где 35' есть рефракция у горизонта, а π обозначает горизонтальный параллакс светила в минутах дуги, или же нужно вычислить t из формулы: sin (π—35')  = sin φ sin δ + cos φ cos δ cos t. Из рисунка нетрудно видеть, что вообще говоря, не все звезды неба восходят и заходят в каждом месте Земли. Звезды, у которых расстояние от полюса, который над горизонтом, равно или меньше высоты полюса над горизонтом (т. е. географической широты места на Земле), не могут заходить под горизонт, и у них не только верхняя, по и нижняя кульминация приходится над горизонтом; напротив, звезды, у которых расстояние от другого, противоположного (что под горизонтом) полюса меньше географической широты (не обращая внимания на ее злак + или —), не могут восходить: они невидимы в этом месте Земли. На каждом из полюсов Земли зенит совпадает с тем или другим полюсом неба, поэтому там звезды не восходят и не заходят: они описывают круги, параллельные горизонту; напротив, на земном экваторе ось мира РР' лежит в горизонте, поэтому все звезды неба там восходят и заходят, и полудневные дуги у всех равны 90°; полусуток каждая звезда находится над горизонтом.  Эклиптика с точкой весеннего равноденствия на ней лежит в основе третьей системы сферических координат, применяемой в астрономии, —  эклиптической. Представим себе (рис. 2) на небесной сфере экватор и полюс Р, точку весеннего равноденствия и эклиптику; точка II небесной сферы, находящаяся на 90° от всех точек эклиптики в северном полушарии неба (т. е. в том, где находятся созвездия Медведиц), называется северным полюсом эклиптики; эклиптика наклонена к т. н. среднему (см. прецессия) экватору под углом ε = (в начале 1900 года) 23° 27' 8”,26, который в наше время ежегодно уменьшается на 0”,4б8; ее полюс II находится на расстоянии ε от полюса Р в созвездии Дракона (см. рисунок при сл. прецессия). Представим себе большой круг небесной сферы, проходящий чрез II и светило s и пересекающий эклиптику в точке L. Дуга Ls называется широтой b светила s, она считается к северу и к югу от эклиптики (т. е. к созвездию Дракона и от него) — северная и южная широта, аналогично с северным и южным склонением, — и выражается в градусах от 0° до 90°; дуга эклиптики L называется долготой I светила s, считается от точки весеннего равноденствия в ту же сторону, как прямое восхождение, и выражается в градусах от 0° до 360°; нетрудно видеть, что если даны широта b и долгота I, то положение точки s на небесной сфере определено вполне. Следующие формулы, получаемые от применения основных формул сферической тригонометрии к треугольнику lIps, показывают связь между l, b, α, δ:

по ним можно вычислить l и b, если известны α и δ; аналогичные формулы применяются для обратного перехода от I и  b к α и δ.

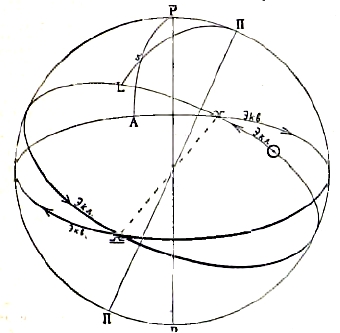
Рис. 2.

Указанные три системы сферических координат суть главнейшие из применяемых в астрономии. Эклиптическая применяется при теоретических исследованиях движений небесных тел в солнечной системе; горизонтальная применяется исключительно в практической астрономии; экваториальная — и в практической, и в теоретической.  Для теоретических исследований нужно бывает знать направления прямых к исследуемому светилу из центра Земли, т. е. геоцентрические сферические координаты светила в известные моменты времени; это совсем не то, что непосредственно дает наблюдение; оно дает направление, по которому наблюдатель на поверхности Земли в известный монет видит светило. Но лучи света, проходя через земную атмосферу, преломляются, и наблюдатель видит светило не по тому направлению, по которому он видел бы его, если бы этого преломления лучей, т. н. рефракции, не было; поэтому нужно уметь освободить сферические координаты, определенные наблюдением, от влияния рефракции. Кроме того, вследствие движения наблюдателя как от движения центра Земли вокруг Солнца, так и от вращения Земли около оси, направление, по которому наблюдатель видит светило, не есть направление прямой линии, соединяющей в этот момент глаз наблюдателя и светило (конечно, по учете рефракции); разница между этими направлениями (видимым и истинным местом светила на небесной сфере) называется аберрацией, и нужно уметь исправить видимые координаты от аберрации. Далее, направление прямой от наблюдателя к светилу в общем случае не совпадает с направлением прямой, соединяющей центр Земли и светило в тот же момент; поэтому нужно уметь из истинных сферических координат, отнесенных к месту наблюдения, вывести истинные сферические координаты, отнесенные к центру Земли, геоцентрические координаты; разница между теми и другими называется параллаксом (см.); нужно, следовательно, освободить наблюдения от параллакса. После всех этих исправлений мы получаем истинные геоцентрические координаты светила на небесной сфере, например, α и δ, отнесенные к тому положению экватора и точки весеннего равноденствия на нем, которое было в момент наблюдения. Но место полюса Р на небесной сфере, а следовательно, в положение экватора на небесной сфере и точки весеннего равноденствия на экваторе меняются с течением времени (т. н. прецессия и нутация; см.), меняется, следовательно, положение самой системы сферических координат, а от этого, независимо от самостоятельного изменения направления прямой от центра Земли к светилу, меняются координаты этого светила на небесной сфере; например, склонение Арктура, главной звезды в созвездия Пастуха, уменьшается ежегодно, около 1915 г. — на 18”,83, но это вовсе не значит, что направление от Земли к Арктуру меняется ежегодно на этот угол; главным образом это изменение склонения происходят от того, что полюс Р удаляется от Арктура, и именно на 16”,83 в год, так что собственное движение Арктура по склонению составляет лишь — 2”,00 в год. Ясно, следует, что для исследования движения небесных светил необходимо, кроме всех упомянутых поправок, учитывать еще влияние на их координаты того обстоятельства, что экватор и эклиптика меняют свои расположения на небесной сфере. Все α и δ какого-либо светила, найденные из наблюдении в разные дни и годы и относящиеся каждый раз к экватору и эклиптике (обыкновенно говорят проще: к равноденствию) момента наблюдения, нужно свести к какому-нибудь одному и тому же положению их, к одному равноденствию. Это приведение делается в два приема: 1) освобождают α и δ, отнесенные к истинному равноденствию (истинное положение экватора и эклиптики) момента наблюдения, от влияния только мутации и получают α и δ, отнесенные к т. н. среднему равноденствию, т. е. к такому положению экватора и эклиптики в момент наблюдения, какое было бы, если бы существовала прецессия, но не было нутации (это деление чисто условное, для удобства рассуждений и вычислений); 2) полученные таким образом т. н. средние α и δ освобождают от прецессии, сводя их к избранному для поставленной задачи среднему же равноденствию какого-либо момента, обыкновенно к началу какого-либо астрономического года, например, года наблюдения, либо началу десятилетия и т. п.; за начало астрономического (т. н. Бесселева) года (annus fictus) считается момент, когда прямое восхождение среднего экваториального солнца, отнесенное к среднему равноденствию и обремененное аберрацией, равняется 18 ч. 40 мин., по продолжительности астрономический год есть год тропический. Не входя в детали вычислений всех этих поправок и приведений, приведем лишь основные законы и (иногда приближенные) формулы.

Рефракция уменьшает зенитное расстояние, так что истинное зенитное расстояние = z + 60”,2(B/760)·(273/273+t°)·tg z, где В — барометрическое давление в миллиметрах, t° —  температура воздуха в градусах Цельсия, z — наблюдаемое зенитное расстояние. Аберрация годичная, от движения Земли вокруг Солнца, приближает светило к той точке небесной сферы (так называемый апекс), в которую направлено движение центра Земли в момент наблюдения, на величину 20”,47 х sin углового расстояния светила от апекса; аберрация суточная, от вращения Земли около оси  приближает светило к точке востока на величину 0”,32.cos φ. sin углового расстояния светила от точки востока; φ — географическая широта места наблюдения.

От параллакса зенитное расстояние, наблюдаемое на поверхности Земли, больше геоцентрического земного расстояния приблизительно на угол π.R.sin s, где π — экваториальный, горизонтальный параллакс (см.) светила, R — расстояние места наблюдения от центра Земли в долях экваториального радиуса Земли, z — наблюдаемое зенитное расстояние. На основании этих простых формул при помощи теорем сферической тригонометрии можно вывести влияние рефракции, аберрации и параллакса на различные сферические координаты.  От прецессии прямое восхождение α и склонение δ какого-либо светила изменяются через один год на величины:

Δα = + 3^δ,0726 — 1^δ,3364 sin α tg δ, Δδ = + 20'',046 cos α; числовые коэффициенты даны для 1915 года; они медленно изменяются с течением времени. Влияние нутации приближенно выражается так:

α, освобожденное от влияния нутации, = α с нутацией +15”,81 sin Ω + 6'',86 sin Ω sin α tg α +9”,21 cos Ω cos α tg δ; δ₁ освобожденное от влияния нутации, = δ с нутацией + 6”,86 sin Ω cos α — 9”,21 cos Ω sin α; здесь Ω обозначает долготу восходящего узла лунной орбиты.

Все эти поправки необходимы для обработки наблюдаемых координат; что касается получения этих последних, то они измеряются при помощи целесообразно построенных угломерных инструментов; не входя в технические детали, укажем лишь основные идеи главных методов, которые для этого применяются. Существеннейшие астрономические наблюдения для определения координат небесных светил производятся во время кульминации светила при помощи меридианного круга (см.) или заменяющих его инструментов (пассажный инструмент и вертикальный круг). С ним можно 1) определить зенитное расстояние в момент кульминации, 2) определить по часам, идущим по возможности точно, момент кульминации. Положим, что наблюдатель определил зенитное расстояние Z_в какой-либо яркой околополярной звезды (например, α Малой Медведицы) в верхней кульминации, и через полсуток (может быть, днем, для того и выбирается яркая звезда, чтоб ее можно было видеть в трубу днем) ее же зенитное расстояние Zn в нижней кульминации; допуская, что полярное расстояние ее в обоих наблюдениях одинаково (малое изменение от прецессии, нутации и аберрации можно вычислить и принять во внимание), замечаем, что полюс Р лежит как раз посредине между первым и вторым положением звезды; следовательно, ½  (Zв+Zn) есть зенитное расстояние полюса Р, точки, явственно па небесной сфере ничем не отмеченной, на которую, следовательно, нельзя навести трубу; тогда 90°— ½ (Zв+Zn) есть высота полюса Р над горизонтом, т. е. (см. Земля) географическая широта с места наблюдения. Кроме того, ½ (Zn-Zв) есть полярное расстояние наблюдаемой звезды, а следовательно, 90° - ½ (Zn-Zв) есть ее склонение. Угол φ   есть также расстояние от зенита до экватора (считаемое по меридиану); положим, что наблюдатель определил еще зенитное расстояние z какого-либо светила между зенитом и точкой юга; тогда, как можно видеть из рис. 1, φ—z есть склонение этого светила; если z есть наблюденное зенитное расстояние светила между зенитом и полюсом, то его склонение δ = φ+z, а для нижней кульминации 90°—δ = z — 90° + φ. Таким путем, измеряя зенитное расстояние в меридиане, можно определить склонение любого светила в момент его кульминации. Одновременно с этим наблюдатель на меридианном круге определяет также и моменты кульминации звезд и других светил по своим часам, которые должны идти по звездному времени (см. выше). Положим, что часы идут совершенно верно, т. е. за звездные сутки делают ровно 24 ч. 0 мин. 0 сек. 00; тогда разности наблюдаемых моментов кульминаций различных звезд суть как раз  разности их прямых восхождений. Если, как это всегда бывает, часы идут неточно (ибо совершенно точных часов нет и по несовершенству человеческому быть не может), то можно определить, на какую долю секунды они за сутки уходят вперед или отстают: для этого через сутки определяют моменты кульминации тех же звезд (теоретически при идеальном инструменте и наблюдателе достаточно было бы одной из них), что и накануне; если часы идут верно, то эти моменты будут те же, что и накануне; если часы разнятся, то эта разница и есть суточный ход часов; конечно, для точности нужно принять по внимание изменения за сутки прямых восхождений от прецессии, нутации и аберрации. Тогда неточность хода часов можно учесть, принимая однако что они и днем и ночью идут одинаково (см. часы), и таким образом получить точные разности прямых восхождений наблюденных звезд и других светил. Тогда, чтоб знать самые прямые восхождения, достаточно знать хотя бы одно из них; будь точка весеннего равноденствия отмечена на небесной сфере какой-либо звездой, дело было бы просто, но этого нет, и потому приходится прибегать к более сложным приемам, а именно, наряду со звездами непременно наблюдать и Солнце, определяя склонение его центра и момент его кульминации. Положим, что около дня весеннего равноденствия (см. рис. 3) в один день определено склонение центра Солнца δ₁ и разность а прямых восхождений Солнца и какой-либо яркой звезды s, и в другой день — склонение центра Солнца с₂ и разность b прямых восхождений Солнца и той же звезды; тогда из чертежа по правилам элементарной геометрии имеем: прямое восхождение звезды = b + δ₂(a-b)/(δ₁+δ). Раз прямое восхождение хотя бы одной звезды известно, то по известным уже разностям вычисляются прямые восхождения всех наблюдаемых звезд.

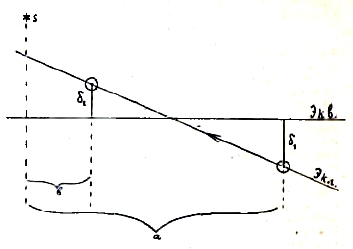
Рис. 3.

Конечно, это рассуждение, чертеж и формула дают лишь идею метода: небесная сфера не плоскость, зависимость разных величин выражается простой пропорцией, на деле нужно применять формулы сферической тригонометрии, а для точности результатов — и другие методы; приведенное рассуждение призвано лишь указать суть вопроса и пояснить, как наблюдения Солнца могут дать то, что нужно для определения прямых восхождений. Если прямые восхождения нескольких звезд известны, то можно определить, на сколько часы идут вперед или отстают, так как в момент кульминации звезды с прямым восхождением α верные часы должны показывать столько часов, мин. и сек., сколько их содержится в α. Наблюдая наравне со звездами другие, подвижные, светила (планеты, Луну, кометы), можно определить и их прямые восхождения, относящиеся, конечно, к моменту кульминации каждого из них.   Более подробно все затронутые вопросы рассматриваются в курсах сферической и практической астрономии; на русском языке курсы профессора Р.Ф. Фогеля (Киев) и профессора А. А. Иванова (Петроград).

Орбита (астрономическая, от латинского orbita — путь), общее название пути какого-либо небесного светила в пространстве, например, пути планеты или кометы относительно Солнца, пути одной звезды в двойной звезде относительно другой и т. п. Эти пути, вообще говоря, представляют сложные кривые, но мало отличаются от конических сечений (эллипс, парабола, гипербола), и потому очень часто орбитой называется коническое сечение, приблизительно представляющее действительный путь небесного светила. 1) Вообразим себе две точки М₁ и М₂ пути и моменты t₁, t₂, когда действительная планета, движущаяся под притягательным действием и Солнца, и других планет, проходит через эти точки; можно определить такое коническое сечение с фокусом в центре Солнца, в котором воображаемая планета под действием только одного, Солнца движется так, что в те же моменты t₁ и t₂ проходит чрез те же точки М₁ и М₂ и лишь немного не совпадает с действительной планетой в другие моменты времени, потому что притягательные силы планет малы в сравнении с притягательной силой Солнца. Это соображение применяется при первоначальном приблизительном определении путей планет и комет относительно Солнца. Математический разбор этой задачи, составляющий предмет т. н. теоретической астрономии, показывает, что если непосредственными наблюдениями даны видимые положения планеты или кометы на небесной сфере в три момента времени, разделенные один от другого несколькими днями или неделями, то возможно вычислить коническое сечение только что указанного характера (первый и третий моменты соответствуют указанным ранее t₁ и t₂); движение воображаемой планеты во этому коническому сечению очень мало отличается от действительного движения планеты, и поэтому, всходя из этой орбиты, предвычисляют наперед движение планеты и таким образом способствуют тому, чтобы можно было легко находить ее на небе и наблюдать. Такой прием всегда применяется к новооткрытым планетам и кометам; обыкновенно первая орбита, полученная по наблюдениям в первые 3—4 дня после открытия, требует некоторого исправления, и это производят по прошествии нескольких недель на основании наблюдений, разделенных друг от друга большим промежутком времени. 2) Вообразим себе положение планеты (или кометы) относительно Солнца в какой-нибудь момент времени и скорость ее в  этот момент; если бы в этот момент прекратилось действие других планет на Солнце и на эту планету, то она, начиная с этой точки, под влиянием уже только одного Солнца описывала бы некоторое коническое сечение, которое прикасалось бы в этой точке к действительному пути ее; движение ее по этому коническому сечению не совпадало бы с действительным, более сложным, движением под действием и Солнца, и планет, но и немного отличалось бы от него, т. к. притяжение планет гораздо слабее притяжения Солнца; такое коническое сечение называется соприкасающейся или оскулирующей орбитой. Вычисление оскулирующей орбиты производится после того, как получено уже достаточно большое число наблюдений планеты или кометы, например, в случае кометы после того, как она перестала быть видимой, удалившись от Солнца. Так как действительный путь светила не есть коническое сечение и даже не есть плоская кривая, то при оскулирующей орбите всегда указывается момент оскуляции, т. е. момент, когда действительное и воображаемое светила находятся в одной точке и имеют одинаковую скорость. Для характеристики орбиты служат т. н. элементы ее. Два из них (долгота восходящего узла и наклонение) определяют положение той плоскости, в  которой расположена орбита, по отношению к плоскости эклиптики в определенную эпоху (положение эклиптики в небесном пространстве медленно изменяется, см. небесная сфера); вообразим себе обе эти плоскости, проходящие через центр Солнца, и орбита в ее плоскости; прямая пересечения этих плоскостей называется линией узлов; орбита пересекает эту прямую в двух точках; в одной из них светило бывает при переходе из южного по отношению к эклиптике полушария неба в северное, и направление из центра Солнца в эту точку называется восходящим узлом орбиты, а направление в другую — нисходящим узлом; угол между направлением из центра Солнца в   точку весеннего равноденствия и восходящим узлом называется долготой восходящего узла и считается от точки весеннего равноденствия так, как вообще все долготы (см. небесная сфера). Угол между указанными плоскостями называется наклонением орбиты к эклиптике; наклонение измеряется от 0° до 180°; представим себе сначала, что обе плоскости совпадают, и движение светила происходит в ту же сторону, как движение Земли вокруг Солнца, тогда наклонение = 0°; при увеличении угла между плоскостями наклонение увеличивается, переходит через 90° (плоскости взаимно перпендикулярны) и, постепенно возрастая, доходит  до 180°: тогда плоскость орбиты опять совпадает с плоскостью эклиптики, но теперь движение светила совершается в направлении обратном направлению движения Земли вокруг Солнца; наклонение планетных орбит  все меньше 90°; у некоторых комет наклонение больше 90°. Третий элемент есть угол между направлениями из центра Солнца в восходящий узел и в перигелий, т. е. ближайшую к Солнцу точку орбиты; он называется расстоянием перигелия от восходящего узла и считается в направлении движения светила по ее орбите от 0° до 360°; у планет иногда дается сумма (долгота восходящего узла + расстояние перигелия от узла), которая называется долгота перигелия (иногда прибавляется: в орбите); этот элемент характеризует расположение орбиты относительно линии узлов. Четвертый и пятый элементы суть: у эллипса — длина половины большой оси и эксцентриситет, у гиперболы — длина половины действительной оси и эксцентриситет; у параболы же, т. к. эксцентриситет всегда = 1, а большая ось бесконечно велика, вместо двух этих элементов фигурирует один: расстояние от центра Солнца до перигелия; этими элементами характеризуются форма и размеры орбиты. Наконец, шестой (а у параболы пятый) элемент указывает положение светила на его орбите в известный момент времени; например, для этого дается момент прохождения светила чрез перигелий. Последними тремя (у параболы двумя) элементами определяется движение светила на его орбите, и, зная их, можно для любого момента определить ту точку орбиты, где оно находится; каждая точка характеризуется двумя величинами: 1) истинной аномалией ее, это есть угол между направлениями из центра Солнца в перигелий и к светилу, и  2) радиусом-вектором, т. е. расстоянием от центра Солнца до светила. В теоретической астрономии выводятся формулы, при помощи которых можно по элементам орбиты для заданного момента вычислить истинную аномалию и радиус-вектор, а затем и гелиоцентрические координаты светила (широту и долготу его); а так как по таблицам движения Земли относительно Солнца можно определить для того же момента гелиоцентрические координаты Земли, то из комбинации гелиоцентрических координат можно вычислить и геоцентрическое положение светила. Из учебников теоретической астрономии укажем новейшие: Т. Bauschinger, «Die Babnbestimmung der Himmelskörper»; А. А. Иванов, «Теоретическая астрономия».

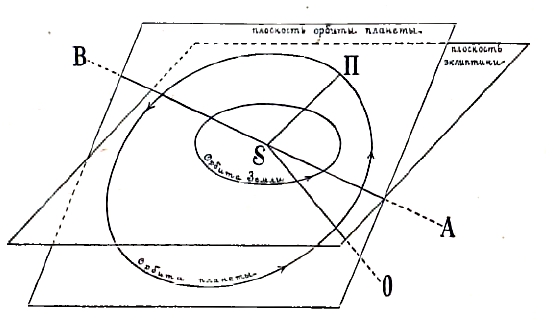
Плоскость эклиптики и пересекающаяся с ней плоскость орбиты некоторой планеты; АВ есть линия пересечения этих плоскостей, на ней находится центр Солнца S; линия SО лежащая в плоскости эклиптики, указывает направление из S в точку весеннего равноденствия; стрелки на орбитах указывают направления движений Земли и планеты; Н есть перигелий орбиты. При указанном на рисунке направлении движения планеты SA есть направление в восходящий узел орбиты, угол OSA есть долгота восходящего узла; наклонение J, как видно из рисунка, менее 90°, угол АSН есть расстояние перигелия от узла. Если же при таком же расположении орбиты движение по ней совершается в обратном направлении, навстречу стрелке, то тогда SB есть направление в восходящий узел, долгота его есть угол ОSB, считаемый от SО в сторону движения Земли, следовательно, он равен OSА + 180°, т. е. больше 180°; наклонение в этом случае больше 90°, оно равно 180°—I; расстояние перигелия от восходящего узла есть угол BSH.

С. Блажко.