Непрерывная дробь

Непрерывная дробь. Непрерывной дробью называется выражение вида:

Числа а_i, b_i подчинены только условию, чтобы выражение Р_n имело смысл.

Отдельные дроби а_i/b_i (b₀ = 1) называются звеньями. Если число звеньев бесконечно, то непрерывная дробь называется бесконечной; когда в такой дроби звенья повторяются в определенном порядке, то непрерывная дробь называется периодической. Всякую непрерывную дробь можно привести в нормальный вид, когда все а_i =+1(i>1). Удерживая одно звено, два и т. д. и производя вычисления, получим подходящие дроби нулевого, первого, второго и т. д. порядков:

причем всегда

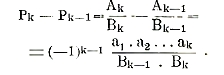
Когда все а_i > 0, b_i > 0, то при возрастании числа и все подходящие дроби четного порядка убывают, оставаясь больше непрерывных дробей, а подходящие др. нечетного порядка возрастают, оставаясь меньше непрерывной дроби. Если даны две неограниченные последовательности чисел а_i, b_i, то составленная из них непрерывная дробь называется сходящейся, если

Причем число Р называется значением бесконечной непрерывной дроби. Так как

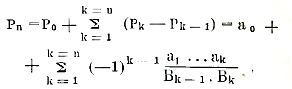
то непрерывная дробь будет сходящейся вместе с рядом

Лежандр доказал, что если а_i и b_i — целые числа, и а_i≥ b_i>0, то соответствующая бесконечная непрерывная дробь всегда представляет иррациональное число, меньшее единицы. Бесконечная непрерывная дробь может быть развернута в бесконечный ряд и бесконечное произведение, и обратно. Сходящаяся периодическая непрерывная дробь, период которой содержит m звеньев (а_i/b_i, …, а_m/b_m), представляет корень квадратного уравнения

B_m–1x² + (B_m – A_m–1)x – A_m = 0, и обратно. Если все a₁=1 и b₁ суть целые положительные числа, то непрерывная дробь называется правильной. Всякую рациональную дробь можно представить в виде конечной правильной непрерывной дроби, а всякое иррациональное число можно обратить в бесконечную правильную непрерывную дробь, причем подходящие дроби будут представлять его приближенные значения. Неправильные дроби имеют большое теоретическое и практическое значение. Так, например, посредством них Ламберт доказал иррациональность чисел е^х , log х при всяком рациональном х; Лаплас выразил через них интегралы уравнений теории приливов. См. Stern, «Lebrbuch der algebraischen Analysis» (1860); Journal für Mathematik», 1833,1834; Legendre, «Тhéоrie des nombres» (1830).

А. Некрасов.