Определитель

Определитель (детерминант) n-го порядка есть схема из nⁿ количеств:

вычисляемая по некоторому закону. Каждое количество а_ik называется элементом определителя; элемент а_ik принадлежит к i—ой строке и к k—му столбцу. Вычисление определителя: составим произведение элементов а₁₁а₂₂а₃₃...а_nn, лежащих на главной диагонали: сохраняя, например, первые указатели, переставим в рассматриваемом произведении всеми возможными способами вторые указатели и будем брать получаемые произведения со знаком + или — в зависимости от того, будет ли перестановка указателей четная или нечетная. Перестановка называется четной (нечетной), если она содержит четное (нечетное) число нарушений возрастающего порядка указателей, или инверсии;  например, а₁₃а₂₄а₃₂а₄₁ содержит 2 + 2 + 1 = 5 инверсий. Определитель Δ_n имеет 1,2...n членов, причем половина из них должна быть взята со знаком +, а половина с —.

Вычеркивая из определителя_Δn i-ую строку и k-й столбец и взяв полученный определитель с множителем (—1)^i+k, мы получим минор первого порядка I_ik определителя Δ_n, соответствующий элементу а_ik. Тем же приемом из миноров I_ik можно образовать миноры второго порядка и т. д. Можно доказать, что определитель разлагается по элементам любой строки или столбца; именно:

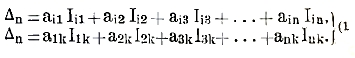
Сверх того

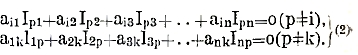
Из последнего вытекает, что определитель, имеющий две одинаковых строки (столбца), тождественно равен нулю, и значение определителя не изменяется, если к элементам какой-нибудь строки (столбца) мы прибавим элементы какой-нибудь другой строки (столбца), умноженные на одно и то же количество. Отсюда получается удобный способ вычисления определителя. Например:

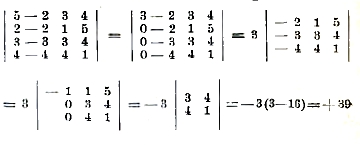
(Операции: прибавление к элементам первого столбца элементов второго столбца и разложение по элементам первого столбца).

Решение системы линейных уравнений приводится к вычислению определителя. Так, умножая уравнение

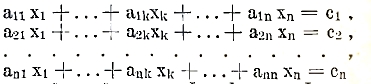
соответственно на I_1k, I_2k, …, I_nk и складывая, получим по (2) и (1)

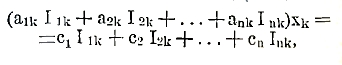
или

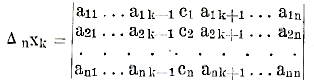
В случае однородных уравнений, когда все с равны нулю, неизвестные х имеют решения, отличные от нуля, только в том случае, если Δ_n = 0; тогда х пропорциональны минорам любой одной и той же строки.

Функциональным определителем, или определителем Якоби называется определитель

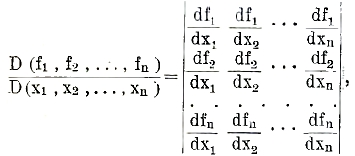
где f₁, f₂, …, f_n суть функции от x₁, x₂, …, x_n. Если D(f₁,…,f_n)/D(x₁,…,x_n) = 0, то между функциями f₁, . . . , f_n существует некоторое соотношение F (f₁ , f₂, . . . , f_n) = 0, не зависящее от x₁,…,x_n. См. Чезаро, «Элементарный учебник алгебраического анализа», кн. I; Нетто, «Начала теории определителей».

А. Некрасов.