Параллельные линии

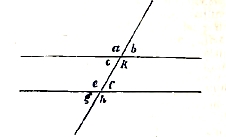
Параллельные линии, линии, лежащие в одной плоскости и не пересекающиеся, сколько бы их ни продолжали в ту или в другую сторону. При пересечении двух параллельных линий третьей получаются 8 углов (см. чертеж), носящих следующие названия: а, b, g и h называемые внешними; с, k, е и f — внутренними; а и g, с и е, лежащие по одной стороне пересекающей прямой, называются односторонними; односторонние углы (а и е, или с и g), из которых один внутренний, а другой внешний, называются соответственными; углы, лежащие по разным сторонам пересекающей, называются накрест лежащими (например, а и h, с и f и др.). Между углами, образуемыми параллельными линиями, существуют следующие отношения: внутренние накрест лежащие углы равны; внешние накрест лежащие углы равны; соответственные углы равны; сумма односторонних углов равна двум прямым углам. Обратно, если существует одно из этих равенств, то линии параллельны.

Основная аксиома о параллельных линиях: через точку, лежащую вне прямой, можно провести лишь одну прямую, параллельную данной (11-я аксиома Евклида). Отрицание этой аксиомы привело знаменитого русского ученого Н. И. Лобачевского к открытию интересных в философском отношении «неевклидовских геометрий» (см. основания математики). Теоремы о параллельных линиях: две линии, параллельные третьей, параллельны между собой; отрезки параллельных между параллельными равны. Линия и плоскость или две плоскости, которые при продолжении не встречаются, также называются параллельными.