Пасхалия

Пасхалия, церковные правила для определения дня празднования святой Пасхи в каждом году. В первые века христианства различные церкви не имели общей пасхалии, и каждая праздновала Пасху, руководствуясь различными соображениями: одни — одновременно с евреями, другие, иногда намеренно, в иные дни, чем евреи; из различия оснований, которыми определялся день Пасхи, выходило, что первые праздновали Пасху раньше (иногда на месяц) вторых; первые получили поэтому название «протопасхитов»; отсюда происходили вполне понятные взаимные неудовольствия и споры, доходившие до объявления протопасхитов еретиками. Наконец, этот вопрос подвергся обсуждению на Никейском (326 г.) соборе. Акты этого собора, если они и были составлены, до нас не дошли, из других же документов того времени, дошедших до нас, ясно, что собор с осуждением отнесся к протопасхитам, постановил, что Пасха везде должна праздноваться в один и тот же день и поручил александрийской церкви наперед устанавливать день Пасхи и сообщать его заблаговременно другим церквам. Были ли собором выработаны или утверждены вполне определенные правила вычисления дня Пасхи — остается неизвестным: несомненных утверждений этого современниками до нас не дошло, и общераспространенное по этому вопросу (в утвердительном смысле) мнение в последнее время некоторые исследователи подвергают сомнению. Как бы то ни было, в александрийской церкви уже ко времени собора установилось правило, что Пасха празднуется в первое воскресенье после первого весеннего полнолуния, весенним же полнолунием считается или то, которое приходится на 21 марта (день весеннего равноденствия), или же первое, следующее за 21 марта. Сообразно с этим правилом составлялись в III, IV и V веках и пасхальные «каноны», содержавшие правила предвычисления и предвычисленные дни Пасхи. Таких канонов, сменявших друг друга, было несколько. Тот, который в конце коцнов был принят во всей христианской церкви и до сих пор применяется в восточной церкви, приписывается св. Кириллу, епископу александрийскому от 412 до 444 г.; этот канон был составлен на время от 437 до 631 г. (по последним исследованиям — до 612 г.) и был затем продолжен Дионисием Малым в VI в. Различие канонов заключалось в способе установления дня пасхального полнолуния; для этого предлагались различные циклы, по истечении которых фазы луны, и в том числе день пасхального полнолуния, повторялись в прежнем порядке. В окончательно принятом церковью каноне для этой цели был принят цикл в 19 лет юлианского календаря, аналогичный Метонову циклу и, вероятно, от него и происходящий. В пределах каждых 19 лет были распределены лунные месяцы по 29 и 30 дней таким образом, что начало каждого календарного месяца довольно близко совпадало с днем действительного новолуния в те века. Получился, таким образом, лунно-солнечный календарь, в котором «пасхальные», т. е. первые весенние, в указанном выше смысле, полнолуния приходились на вполне определенные числа марта или апреля, и эти дни пасх, полнолуния повторялись и повторяются в прежнем порядке через 19 лет; эти дни зависят, следовательно, от номера года в этом 19-летнем цикле; для установления этого номера за 1-ый год «цикла» был принят тот, в котором январское новолуние приходилось на 23 января (а мартовское на 23 марта); таким годом в принятой схеме был, между прочим, 1-ый год до Рождества Христова; номер года в цикле получил название: «золотое число»; отсюда правило: если N есть номер года общепринятого летосчисления от Рождества Христова, то остаток от деления N+1 на 19¹⁾ есть золотое число а; условно это обозначается так:

а = R(N+1/19), R — означает остаток; в византийской церкви было принято иное начало «лунного цикла», на 3 года позже, номер года в нем называется в нашей церкви «круг луны» и определяется по формуле: круг луны,

с = R(N-2/19).  Если дано золотое число или круг луны, то день пасхального полнолуния можно вычислить, если знать распределение 29-ти и 30-дневных лунных месяцев в 19-летнем цикле.

¹⁾ Если N+1 делится на 19 без остатка, то считается, что остаток есть 19, т. е. равен делителю; ток же и в других, ниже встречающихся, аналогичных случаев.

В приведенной таблице для каждого круга луны с и соответственного золотого числа а даны дни пасхальных полнолуний. Если для какого-либо года день пасх, полнолуния известен, то для определения дня Пасхи нужно только знать, на какие числа марта и апреля в этом году приходятся воскресенья. В юлианском календаре через каждые 28 лет (28 = 4х7, 4 - период юлианского летосчисления, 7 — период дней недели) дни недели приходятся на прежние числа месяцев. Сообразно с этим введен 28-летний период, и в восточной церкви по отношению к юлианскому летосчислению он был так расположен, что 9-ый г. по Рождеству Христову оказывался 1-м годом солнечного цикла; номер года в этом цикле называется «круг солнца», и получается правило: круг солнца С = R(N-8/28); в 1-м году этого цикла первое воскресенье в марте приходится на 3-е марта; в приведенной таблице указаны числа 3-го мартовского воскресенья, соответствующие всем 28-ми кругам солнца.

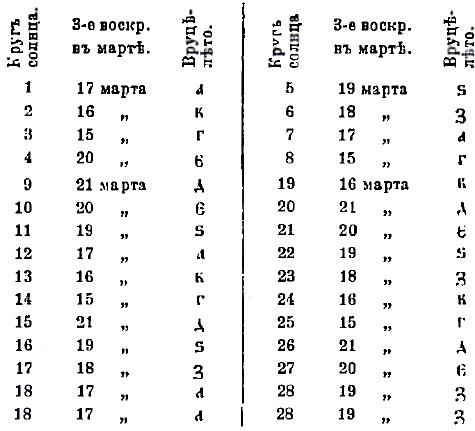
С помощью этих двух таблиц определение дня Пасхи в восточной церкви производится так: вычисляют круг луны, с, и находят число пасхального полнолуния; вычисляют круг солнца, С, находят дни воскресений в марте и апреле; из них первое воскресенье после пасхального полнолуния есть день Пасхи. Например, для 1916: N=1915;

с = R(N-2/19) = 13; C = R(N-8/28) = 3; пасхальное полнолуние 21 марта, 3-е воскресенье в марте —  15 марта, а следующее, 22 марта приходится после пасхального полнолуния и, следовательно, день Пасхи. Так как день Пасхи зависит от двух несоизмеримых периодов, 19 и 28 лет, то периодом его является 532 г. (19х28), который называется великий индиктион; через 532 г. дни Пасхи в марте и апреле повторяются в прежнем порядке. Заметим, что в византийском летосчислении, начинающемся с 5508-го г. до Рождества Христова, первый год есть первый год и круга луны, и круга солнца, и великого индиктиона; поэтому в восточной церкви теперь считается 14-ый индиктион, начавшийся с 1409 г. по Рождеству Христову (5508+1408=532х13).

Так как соответствие 235 лунных месяцев с 19-ю годами юлианского календаря только приблизительное, и приблизительно за 300 лет образуется ошибка в 1 день, то полнолуния, вычисленные по правилам пасхалии, теперь уже не согласуются, как прежде, с действительными полнолуниями на небе, они получаются приблизительно на 4 дня позже действительных. С другой стороны, т. к. весеннее равноденствие не приходится уже теперь по юлианскому календарю на 21 марта, то церковные полнолуния не всегда бывают первыми после действительного равноденствия. Это именно несоответствие вычислений с действительностью, замеченное в средние века, и привело к реформе календаря. При этом и правила вычисления пасхальных полнолуний были изменены с целью большего приближения к действительности и, понятно, должны были стать сложнее, так что в западной церкви нет такой простой периодичности дня Пасхи, как в восточной (532 г.), там этот период = 10 000 лет. От различия вычисления (принцип: первое воскресенье после весеннего полнолуния был, конечно, сохранен) происходит, что дни Пасхи в обеих церквах иногда совпадают, иногда расходятся. В церковных календарях даются еще: эпакта, основание, вруцелето, ключ границ, индикт.

Эпакта какого-либо года указывает, какого числа марта следующего года оканчивается лунный месяц календаря, притом в эпоху установления пасхального канона; основание какого-либо года указывает число дней лунного месяца, протекших к 1-му марта этого же года в более позднюю эпоху, когда ошибки 19-летнего цикла были исправлены на 3 дня; оба числа характеризуют расположение месяцев лунного года на месяцах солнечного; из них можно вычислить день пасхального полнолуния, но он прямо дан в таблице. Каждому дню года приписана навсегда одна из семи букв церковно-славянского алфавита. Эти буквы, начиная с 1 марта, идут в таком порядке:

и т. д., повторяясь: значит, если бы знать, какой букве в заданном году соответствуют воскресенья (эта буква и называется вруцелето), то мы бы знали вообще, как распределяются дни недели в этом году; это достигается тем, что каждому году в 28-летнем круге солнца приписана надлежащая «воскресная» буква. В вышеприведенной таблице для каждого круга солнца указано вруцелето. Для наиболее простого применения вруцелета нужно, как это и делается в восточной церкви, считать начало года с 1 марта, а январь и февраль гражданского года относить к предыдущему мартовскому году; тогда 29 февраля будет последним днем в году и для всякого года, как простого, так и високосного, будет одна воскресная буква; если же, как в западной церкви, год считать с 1 января, то у високосных годов непременно должны оказаться две воскресные буквы: одна для января и февраля, другая — для прочих месяцев. Каждому из 35-ти дней марта и апреля, на которые вообще может падать день Пасхи, начиная с 22 марта и кончая 25 апреля, приписана буква церковно-славянского алфавита по их порядку в алфавите; эти буквы называются ключ границ; сказать, что в каком-либо году ключ границ есть г, все равно, что сказать: в этом году Пасха — 25 марта, и т. п. Индикт — есть номер года в 15-летнем цикле, начинающемся с 313 г. по Рождеству Христову, так что индикт i = R(N-312/15); индикт не имеет никакого отношения к пасхалии, но указание индикта, а также, хотя реже, золотого числа, круга луны, круга солнца, часто сопровождает указание года в средневековых летописях и поэтому имеет значение для хронологии.

С. Блажко.