Приливы и отливы

Приливы и отливы. На берегах океана можно наблюдать, что уровень воды в течение суток дважды подымается и дважды опускается; между каждым поднятием и опусканием уровня проходит приблизительно 6 часов. Самое высокое стояние уровня называется полной водой, самое низкое — малой водой; как полная, так и малая вода бывает дважды в сутки. Явление поднятия уровня от малой воды до полной называется приливом, понижение уровня от полной воды до малой — отливом. Вертикальное расстояние между уровнями полной и малой воды называется амплитудой прилива. Под именем высоты полных и малых вод обозначают поднятие уровня над принятым для карт нулем глубин (так, для карт Мурмана ноль глубин принят на 7,05 фут. ниже среднего уровня моря). Обычно за нуль глубин принимают на картах средний уровень самых низких малых вод.

Ближайшее наблюдение показывает, что время наступления как полной, так и малой воды падает каждый день на другой час, а именно, в сравнении с предыдущим днем запаздывает приблизительно на 40—50 минут. Так, на Мурмане, в Екатерининской гавани, утренняя полная вода 4 (17) июля 1910 г. наблюдалась в 3 ч. 5 мин. утра, а на следующий день, 5 (18) июля, уже в 3 ч. 57 мин. утра, т. о. на 62 мин. позже. В среднем же для Екатерининской гавани промежуток между двумя последовательными полными или малыми водами равен 12 ч. 26 мин. Отсюда ясно, что приливы и отливы в своем ходе сообразуются не с солнечными сутками, а с лунными, продолжительность коих равна 24 ч. 50 мин. У же древним (Страбон) была известна связь между приливами и отливами, с одной стороны, и фазами луны, с другой. Исследования Ньютона показали, что причина явления заключается в притяжении, оказываемом солнцем и луной на легкоподвижную водную оболочку вращающейся вокруг солнца земли. Главное влияние оказывает луна; хотя ее масса в 27 миллионов раз меньше массы солнца, но луна в 388 раз ближе к земле, чем солнце; поэтому приливоотливная сила  луны оказывается в 2,17 раз более сильной, чем солнца. Хотя приливы и отливы главным образом повинуются луне, но, конечно, и солнце оказывает на них заметное влияние, и результаты такого совокупного влияния легко обнаружить. Оказывается, что высота полных и малых вод изо дня в день не одинакова, а меняется: когда солнце и луна находятся на одной линии, т. е. в сизигии, все равно в соединении или противостоянии, тогда, амплитуда прилива оказывается наибольшей, так как действия луны и солнца соединяются; это бывает в новолуние и полнолуние. Напротив, когда луна и солнце бывают в квадратуре, когда влияния их противодействуют друг другу, тогда высота прилива оказывается наименьшей; это бывает во время 1-й и последней четверти луны. Так для Екатерининской гавани в январе  и феврале (старого стиля) 1910 г. мы имеем два максимума высоты полных  и малых вод и два минимума, выражающиеся для вечера так:

Мы видим из этой таблицы, что амплитуда прилива в полнолуние и новолуние достигает наибольшей высоты (10,0—10,6 фут.), а во время 1-й и последней четверти — наименьшей (3,7—6,6 фут.). Явление это носит название полумесячных неравенств приливов и отливов. Наиболее высокая полная вода за полумесяц называется сизигийной полной водой (vives eaux, Springtide, springtide), низшая — квадратурной полной водой (mortes eaux, Nipptide, neap tide). Кроме полумесячных неравенств, имеются еще суточные, выражающиеся в том, что высота утренней полной воды не равна высоте вечерней за те же сутки, как это видно из следующей таблички для Екатерининской гавани за 19 ноября 1910 г. старого стиля:

Полная вода:

7 ч. 25 мин. -  утра 10,0 фут.;
7 ч. 27 мин. вечера – 11,4 фут.;
Разница – 1,4 фут.

Малая вода:

1 ч. 27 мин. ночи – 3,4 фут.;
1 ч. 12 мин. дня – 3,5 фут.;
Разница – 0,1 фут.

Объяснение суточного неравенства заключается в том, что путь луны не совпадает с экватором, а составляет с эклиптикой угол в 5°8’; как следствие, наибольшая высота прилива приходится обычно не на экватор, а на ту широту, для которой луна в данное время в зените. Так как земля вращается вокруг своей оси, то за большим приливом через 12 часов наступает малый. Дважды в течение 27 ¼  суток луна проходит через экватор, и дважды за это время суточного неравенства, обязанного луне, не бывает. А кроме того, и путь земли (эклиптика), как известно, не совпадает с экватором, и склонение солнца меняется от +23 ½° до —2З ½°; только дважды в году, в весеннее и осеннее равноденствие, солнце бывает на экваторе. В соответствии с этим, и амплитуда приливов, и время наступления полных и малых вод меняется. Но, кроме того, на высоту приливов и отливов оказывает влияние расстояние луны и солнца от земли, которое в течение года меняется (параллактическое неравенство). Зимой, когда солнце в перигелии, солнечные приливы выше, чем летом. 2 января расстояние земли от солнца равно 22 949 земным радиусам, 2 июля — 23 731; сообразно с этим, январская приливная сила солнца относится к июльской как 110,6 к 100. Расстояние луны от земли изменяется количеством от 57,03 до 63,66  земных радиусов; сообразно с чем и отношение приливной силы луны меняется как 100:139. Формы приливо-отливной кривой, зависящие от луны, повторяются через 18,6 лет, зависящие от солнца — через 20 800 лет.

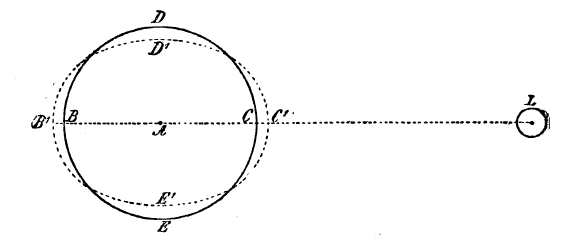
Рис.

По теории Ньютона (или т. н. теории равновесия) приливы и отливы следует представлять себе следующим образом. Допустим, что земля сплошь покрыта океаном равномерной глубины. BDCE окружность земли, L луна, расположенная на экваторе. В точке С частицы притягиваются к луне сильнее, чем в центре А; они поэтому стремятся приблизиться к луне, сила притяжения преодолевает центробежную силу, и в точке С образуется выпуклина, прилив: С перемещается в С'. Напротив, в точке В, наиболее удаленной от L, притяжение наименьшее, центробежная сила берет верх, и частица В стремится удалиться от центра, перемещаясь в В'; здесь тоже образуется выпуклина. Таким образом, в точках, удаленных друг от друга на 180°, прилив наступает одновременно¹⁾.

¹⁾ Если бы земля была неподвижным телом, т. е. если бы не было центробежной силы, то выпуклина образовалась бы только на стороне, обращенной к луне.

Что касается полюсов, т. е. точек D и Е, то в то время как в В и С наблюдается прилив, здесь имеет место отлив; это объясняется тем, что масса воды, необходимая для образования выпуклин у В и С, стягивается с полюсов. Но, кроме того, вода стягивается и с мест, лежащих к востоку и западу от В и С, и больше всего, очевидно, с мест, лежащих по экватору на 90° от В и С; здесь тоже и будет отлив. Из этого ясно, что высота прилива должна быть больше, чем  соответственная высота отлива, что действительно и имеет место. Так как земля в течение 24 часов обращается вокруг своей оси, то в каждом данном месте через каждые 12 час. бывает полная вода и через 12 — малая. Если представить себе землю покрытой сплошь океаном, то можно вычислить, что высота прилива, производимого в С солнцем, составит 168 мм, а луной 364 мм, всего, следовательно, в сизигий 532 мм. В точке В прилив почти такой же. Что же касается отлива, как на полюсах, так и на 90° к востоку и западу от В и С, то вычисление показывает, что он вдвое меньше, чем прилив в В и С, т. е. для солнца 84 мм, для луны 182 мм, а всего, в случае максимального отлива, 266 мм. Наибольшая амплитуда прилива составит таким образом 632 + 266 мм = 799 мм. Все эти вычисления относятся к теоретически возможным приливам, при допущении сплошного океана одинаковой глубины. Но присутствие материков и неравномерность глубин вносит на практике существенные изменения. Кроме того, в предыдущем изложении допускалось, что образовавшийся водный эллипсоид все время находится в состоянии равновесия, чего на самом деле нет. Далее, не приняты во внимание: различная плотность масс воды и суши, инерция водных мисс, трение частиц воды друг о друга, о дно и о берега, притяжение частиц внутри водного эллипсоида. Все это на практике так усложнит явление, что предсказать теоретически для данного пункта берега высоту и время наступления полных и малых вод является невозможным. Лаплас усовершенствовал теорию Ньютона, рассматривая приливы как явление динамическое, своего рода грандиозные волны; в том же направлении пошел далее Эйри (Airy). Наконец, некоторые смотрят на приливы и отливы как на стоячие волны, или сейши (ем).

На практике максимальные (сизигийные) полные воды не падают на день новолуния или полнолуния, а запаздывают на 1—2 ½  дня. Кроме того, полная вода никогда не совпадает с моментом прохождения луны через меридиан. Разница во времени между кульминацией луны и солнца в день новолуния и полнолуния и следующей за ней полной водой называют прикладным часом. Эту разницу нужно прибавить к полудню, чтобы получить время наступления полной воды во время сизигия. Зная прикладной час для сизигия, легко приблизительно вычислить время наступления полной воды для любого дня, если приложить некоторые поправки. Для Екатерининской гавани на Мурмане прикладной час равен 6 ч. 56 мин. Высоту же полных и малых вод знать наперед чрезвычайно трудно. Ее можно вычислить, располагая наблюдениями в данном месте за известный промежуток времени, при помощи гармонического анализа.   В некоторых местах, вследствие интерференции приливоотливных волн, происходящей от влияния конфигурации берегов, приливы и отливы наблюдаются только раз в сутки; это имеет место, например, в северной части Амурского лимана, в устье Мезени и др. На Таити интерференция ведет к тому, что лунная приливоотливная волна совсем исчезает, и развиваются только солнечные приливы и отливы. На океанических островах приливные амплитуды обычно невелики: на острове Св. Елены 0,9 м, на острове Вознесения 0,6 м, Таити 0,4 м. Напротив, на берегах континентов, особенно в бухтах, вдающихся клином в сушу, прилив бывает особенно высок. Наивысшие приливы в Европе бывают в Англии, именно в Бристольском канале до 16 м, во Франции в заливе С. Мишель до 11 м и, наконец, в Северной Америке в бухте Фунди (между Нов. Брауншвейгом и Нов. Шотландией) до 16—16 м. Приливы и отливы выбывают у берегов точения (см). См. G. Н. Darwin, «Ebbe und Flut» (1912, 2 изд.); F. Bidlingmaier, «Ebbe und Flut» (1908); О. Krümmel, «Handb. d. Ozeanographie» (II, 1911).

Л. Берг.