Пропеллор

Пропеллор (с латинского propеllo — гоню вперед), движитель; в широком смысле понятие может быть применено ко всем движущим аппаратам: автомобильное колесо, горящая смесь в ракете, гребное колесо, гребной винт. В русской технической литературе термин пропеллор удержался лишь за гребным винтом (см.) преимущественно воздушным, см. приложение.

Пропеллер

Рассматривая в общем случай пропеллера, как механизм опирающийся на жидкость с силой Р и движущийся в ней со скоростью V, причем площадь сечения струи ABCDЕF (рис. 1), захваченной пропеллером, будет F, получим следующую картину: весьма далеко впереди пропеллера, в сечении AD, скорость жидкости относительно пропеллера равна скорости движения V; в плоскости пропеллера, в ВЕ, скорость будет несколько больше V₁ = V+u; весьма далеко позади пропеллера в СF, жидкость получит полное приращение скорости u₂, так что V₂ = V+u₂. Секундная масса протекающей через пропеллер жидкости будет m = ρFV₁, где ρ – плотность, т. е. масса единицы объема жидкости. Для воздуха ρ = 1/8 kg.sec².mt^-4, для воды ρ = 102 kg.sec².mt^-4. Сила тяги равна секундному приращению количества движения: P = mu₂ = ρFV₁u₂. Затраченная работа

T_m = m/2(V₂² – V²) = mu₂(V+u₂/2).

Полезная же работа T_u = PV = mu₂V. Здесь мы рассматриваем идеальный пропеллер – без потерь на трение жидкости, на удар и на закручивание ее, и все-таки видим, что коэффициент полезного действия

[η] = T_u/T_m = V/(V+u₂/2) всегда меньше единицы. Отсюда теорема: при всяком реакционном пропеллере подвижность точки опоры вызывает потерю в коэффициент полезного действия. Из другого выражения затраченной работы: Tm = PV₁ = P(V+u) находим 2u = u₂, и, следовательно, пропеллер находится в том месте струи, где приращение скорости равно половине полного ее приращения. Следовательно, пропеллер подсасывает к себе жидкость, которая, пройдя через него, еще продолжает ускоряться. Предположение, что пропеллер входит в невозмущенную жидкость, и все приращение ее скорости происходит на протяжении его лопастей, неточно.

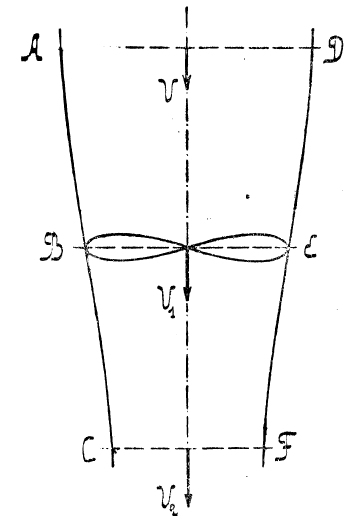
Рис. 1

Инженеру С. К. Джевецкому принадлежит весьма плодотворная мысль рассматривать винт как бы разрезанным соосными цилиндрами на небольшие участки (рис. 2), причем считать каждый элемент лопасти, работающим независимо от других в потоке,  полученном через развертывание цилиндрической поверхности в плоскость. При этом поступательная скорость V для всех элементов одинакова, и скорость жидкости по отношению к лопасти выражается формулой:

W = √V²+(Ωr)², где Ω=2πn/60 есть угловая скорость винта и r – расстояние рассматриваемого элемента от оси винта. Разлагая действующую на элемент лопасти силу Q на составляющие Х и Y по направлению винтовой линии и по нормали к ней (причем сила Х зависит от трения жидкости о лопасть и в идеальной жидкости равна нулю), легко можно составить выражения для силы тяги и работы мотора на весь винт. Тэйлор приноравливает эти формулы к подсчету существующих винтов настоянного шага при произвольно заданной форме и ширине лопастей, С. К. Джевецкий приноравливает их к проектированию новых винтов, причем ставит условием, что шаг может быть переменный, но угол встречи β (между хордой лопасти и касательной на винтовой линии) должен быть постоянный и притом лучший, при котором отношение μ = X:Y было бы наименьшее; ширину лопасти он принимает постоянной (С. К. Джевецкий, «Теория воздушных винтов»). Остроумие идеи вызвало широкую известность и распространение винтов Джевецкого водяных и воздушных (см. XVI, 4 75/76, приложение, рис. 6), но вычисления не вполне совпадали с действительностью: вследствие преуменьшенного значения для скорости подходящей к винту слишком вновь спроектированные винты получались у жидкости малого шага, вычисленные же по Тэйлору работа и сила тяги при заданных скорости и числе оборотов для винтов существующих получались более наблюденных (Харкевич, «Гребной винт в теории и действительности»). Работу мотора и тягу для винтов, работающих на месте (а point fixe) можно было вычислять, но непонятно было, откуда к ним подходит жидкость.

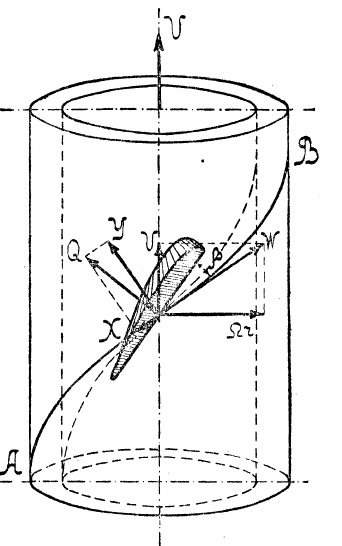
Рис. 2.

Студенты Императорского Московского Технического Училища Сабинин и Юрьев первые (в 1911 г.) стали проектировать винты, приняв во внимание подсасывание и подбирая ширину лопасти под условием, чтобы вся сметаемая винтом площадь была нагружена равномерно (т. е., чтобы u₂=const).

Рис. 3.

Профессор Н. Е. Жуковскому удалось (в 1912 г.) охватить математическим анализом явление, происходящее около гребного винта, и дать правильную теорию его.

Рис. 4.

Основанием к этой теории послужили опубликованные О. Фламмом («Судовый гребной винт и его действие в воде», русский перевод, 1910) моментальные фотографии с моделей гребных винтов, работающих в наполненном водой бассейне со стеклянными стенками. Из гидродинамики известно, что находящийся в воде воздушный пузырек двигается в сторону, в которую давление понижается, и не выходит из области, где давление minimum; известно также, что на осях вихревых нитей имеется minimum давления; на них, следовательно, и должен скопляться находящийся в воде воздух. Именно такое явление обнаруживается на фотографиях Фламма (см. XVI, 475/76, прил., 4, рис. 7) располагающийся за винтом воздух собран на осях вихревых шнуров — винтовых, сходящих с концов лопастей, и осевого, идущего от втулки. Если вместо лопастей представить такие же вихревые шнуры, то можно определить изменение потока, вызванное совокупностью всех вихрей, и развивающиеся при этом силу тяги и работу мотора для всего винта в жидкости без трения. Ширину, форму сечения и углы наклона лопастей на разных радиусах нужно определять под условием, чтобы лопасти развивали те самые вихри, которые были заданы в начале подсчета. Влияние трения, взятое сначала приближенно, вычисляется затем точно, по выяснении формы лопастей. Манера подсчета сохраняется такая же, как у Джевецкого — по элементарным дужкам между радиусами r и r+dr, причем обычно налагаются условия u₂=coust. Т. к. действующие на винт силы вполне известны, то возможен точный подсчет его на прочность. Условия прочности не позволяют соблюдать постоянный угол встречи; шаг винта также получается переменным. Подсчет нескольких испытанных в лабораториях винтов в самом трудном для теории случае — а point fixe — и опыты, произведенные над винтом типа Н. Е. Жуковского в Аэродинамической лаборатории Императорского Технического Училища (также а point fixe) показали правильность созданной им «Вихревой теории гребного винта» («Труды Отд. Физ. Наук О. Л. Е., А. и Э. в Москве», т. XVI и XVII). Построенные на основании ее воздушные винты (рис. 3) на испытаниях показали преимущественно перед винтами Шосьера (рис. 4).

Вернемся к теории идеального пропеллера. Замечая, что Р:ρF=u₂V₁, разделим обе части равенства на квадрат скорости движения; тогда получим отвлеченный коэффициент нагрузки на ометаемую винтом площадь

отсюда находим коэффициент колесного действия идеального пропеллера:

Коэффициент полезного действия действительных пропеллеров, конечно, ниже идеального и для лучших воздушных винтов в пределах функционирования их (0,2 < В < 2,0) может быть приблизительно выражен формулой: η = [η]—0,15, где последний член идет на образование вихрей и на трение. Для водяных винтов разность [η]—η значительно больше нередко превышает 0 4 (см. Харкевич). Столь большая потеря часто может быть объяснена явлением кавитации, т. е. разрыва жидкости с образованием пустоты позади лопастей. В воздушных винтах кавитация не имеет места: чтобы водяной винт работал в таких же условиях относительно кавитации, как воздушный, надо представить его работающим в воде под давлением 800 атмосфер. На рис. 5 представлена кривая коэффициента полезного действия идеального пропеллера, а также самая верхняя и самая нижняя из кривых коэффициентов полезного действия двадцати лучших воздушных винтов, испытанных в аэродинамической лаборатории Эйфеля в Париже. Из нее видно, что наибольший коэффициент полезного действия винтов получается при В равном приблизительно 0,2; при еще меньших значениях В трения начинают играть преобладающую роль. Винты Н. Е. Жуковского дают высокий коэффициент полезного действия и при очень малых В; но, чтобы осуществить винт, работающий при малом значении коэффициента В, надо сделать его очень большим, что иногда невозможно вследствие недостатка места; для деревянных воздушных винтов с большим числом оборотов, кроме того, трудно удовлетворить условиям прочности.

На различных судах военного флота значения коэффициента В меняются от 0,1 до 0,5, на аэропланах различных систем при нормальном горизонтальном полете В меняется от 0,15 до 0,4; таким образом, коэффициент В численно одинаков для правильно функционирующих винтов как водяных, так и воздушных.

Если бы полезная мощность Т^u возрастала точно с кубом скорости, то коэффициент В на данном аппарате оставался бы постоянным при всех скоростях; так бывает на подводных лодках и дирижаблях при горизонтальном перемещении. На кораблях, вследствие лобового сопротивления, полезная мощность растет быстрее, нежели с кубом скорости; приближенно

(Афанасьев); поэтому на кораблях В несколько растет со скоростью.

Аэроплан находится в условиях, совсем отличных от указанных: скорость его полета должна быть такова, чтобы поддерживающая сила крыльев была равна весу аппарата (Дюшен, «Технические беседы об аэроплане»). Меня при помощи руля высоты угол встречи главных планов, можно достигать этого при различных скоростях. При этом, если тяга винта больше необходимой для поддержания аэроплана, то аэроплан будет подниматься, причем составляющая его веса на направление полета поглотит избыток тяги винта; если тяга винта меньше, то аэроплан будет снижаться, и составляющая веса пополнит недостаток тяги. Т. н. авиационные моторы в огромном большинстве случаев все время развивают свою максимальную мощность, но аэроплан летит горизонтально или под данным углом к горизонту с вполне определенной скоростью, причем как нетрудно сообразить по рис. 5, положив мощность мотора T_m постоянной, тяга винта при уменьшении скорости возрастает, при увеличении его падает. Вследствие такой особенности аэроплана коэффициент нагрузки за ометаемую винтом площадь на одном и том же аппарате резко меняется при разных режимах полета, начиная с отрицательных значений при планирующем спуске, когда мотор выключен и винт вертится, как мельница, и возрастая до значения учетверенного против нормального при быстром подъеме, когда скорость полета значительно уменьшается.

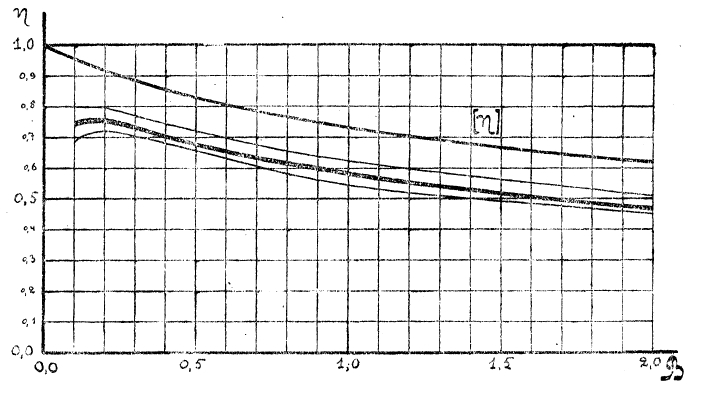
Рис.5

Рассмотрим еще один важный фактор, характеризующий работу пропеллера – скольжение (recul). Винтовой пропеллер постоянного шага Н, двигаясь в жесткой гайке, прошел бы за секунду путь NH, где N число оборотов винта в секунду. В действительности он проходит путь V; отношение S=N(H-V)/NH называется скольжением винта, притом кажущимся, если винт находится за кормой корабля, в спутной струе (см. гребной винт). Т. к. скорость спутной струи – величина весьма неопределенная и неизмеренная, то лучше иметь дело с кажущимся скольжением, наивыгоднейшая величина которого задается в зависимости от обводов корабля, числа винтов и расположении их относительно кормы, от 0,06 до 0,28; верное для тяжелых, тихоходных судов, второе для очень быстроходных – крейсеров, миноносцев (Харкевич, на основании опытов Fligge и собственных).

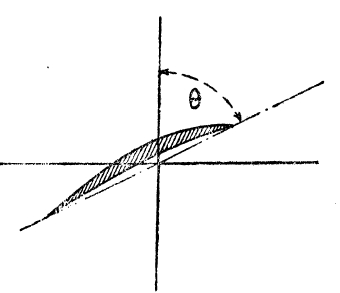
Рис. 6.

Рассматривая формулу скольжения, мы видим, что шаг гребного винта выбирается не произвольно, но есть величина вполне определенная, связанная, главным образом, с числом оборотов его и со скоростью судна. Выясним поэтому понятие о шаге винта. В геометрическом винте шагом называется тот путь, который бы винт прошел параллельно своей оси в соответствующей ему гайке за один оборот. Если такой винт (представляющий очень тонкую винтовую поверхность), вращаясь в воздухе, будет двигаться поступательно так, как он двигался бы в неподвижной гайке, то он не будет возмущать воздуха и не разовьет силы тяги. Поэтому можно сказать, что шаг геометрического винта равен тому пути, который пробегает винт за время одного оборота при отсутствии силы тяги. Формулой это выразится так:

В винте, для которого нельзя указать соответствующей гайки, принято шаг винта характеризовать динамически, именно: по аналогии с геометрическим винтом, шагом винта произвольной формы называют путь, который проходит  он за один оборот, когда его сила тяги равна пулю. При таком определении шага уравнение (3) будет иметь силу не только для геометрического винта, но и для винта любой формы.

Рис. 7.

Обычно шаг винта определяют по углу Θ наклона лопасти к образующей цилиндра (см. рис. 6):

Так весьма удобно чертить и строить винты; но это значение шага не будет соответствовать динамическому шагу Н, определяемому по уравнению (3). Из аэродинамики известно, что вогнутая пластинка, которая движется в воздухе параллельно своей хорде, имеет еще некоторую подъемную силу, перпендикулярную к направлению встречного потока и обращенную в сторону выпуклости пластинки (рис. 7); согласно с рис. 1, эта сила Y дает винту еще некоторую силу тяги по направлению оси винта. Чтобы подъемная сила вогнутой пластинки была равна нулю, необходимо, чтобы встречный воздух ударял на нее сверху под некоторым углом β₀ к ее хорде (см. рис. 8), равным обычно 3—5°. Из этого следует, что тяга винта равна нулю, когда  воздух в относительном движении набегает на его лопасть под углом Θ— β₀ образующей, как на рис. 9. Такое толкование соответствует понятии о динамическом шаге винта, который выражается формулой

Отсюда видим, что для исполняемых на практике винтов динамический шаг Н₀ всегда больше шага Н, которым обычно оцениваются винты. По испытаниям, произведенным в лаборатории Эйфеля над воздушными винтами при отношении шага к диаметру от 0,5 до 1,26, оказалось, что динамический шаг более определяемого по хордам на 25—15%; это дает для угла β₀ значения 3—5°, т. е. такие же, как и по наблюдениям над моделями аэропланных крыльев в потоке воздуха. Указанное превышение динамического шага над принятым для характеризования винта при построении делает понятным заявление некоторых авторов, что винты иногда работают при скольжении равном нулю и даже отрицательном, тогда как теоретически непременным условием существования силы тяги является положительное и не равное нулю скольжение винта, ибо иначе прошедшая через него жидкость не будет отброшена назад в абсолютном движении.

Рис. 8.

В теории идеального пропеллера средним скольжением называется отношение

ρ_μ = u/V₁, откуда следует, что идеальный коэффициент полезного действия

Если бы скорость возрастала от V до V₂ не непрерывно, но мгновенно, скачком, то на удар тратилась бы дополнительная работа mu₂²/2, т. ч. в этом случае мы имели бы коэффициент полезного действия

[η]_y = V/V₂ = 1-ρ, где ρ = u₂/V₂ называется просто «скольжением» (Polland et Dudcbout, “Théorie du navire”). Последнее равносильно скольжению NH-V/NH, если бы жидкость сходила с геометрического винта в направлении касательных к его лопастям; но это предположение точно лишь для пропеллера с большим числом весьма тонких лопастей.

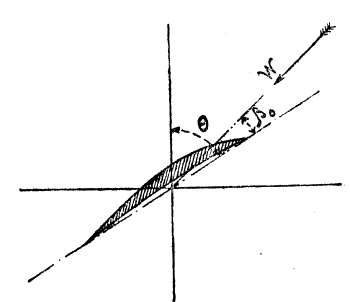
Рис. 9.

А. Н. Харкевич приводит предложенный Fligge способ расчета корабельных винтов: кажущееся скольжение выбирается, как было указано. Сила тяги определяется по формуле сопротивления судна или же по формуле:

P = 75N_eη/V = 145,8N_eη/W; здесь N_e – эффективная мощность (в НР) машины на валу винта, равная приблизительно 0,85N_i, где N_i мощность индикаторная; η – к.п.д. собственно винта, V и W – скорость судна в м/сек и в узлах (или морских милях в час; морская миля 1852 м); оба определения тяги должны совпадать. Упорное давление   р на единицу проектированной (на плоскость вращения) площади лопастей выбирается по типу судна от 0,5 kg/cm² для тяжелых до 1,70 kg/cm² для легких и быстроходных судов. Индикаторная мощность и число оборотов машины в минуту n считаются данными; остается определить (в метрах) диаметр и шаг винта Н (последний предварительно уже определен по скольжению, но может быть несколько изменяем), что делается по формуле

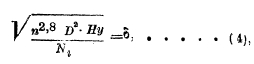
где показатель уменьшается от 2,52 до 2,42, а коэффициент δ – от 446 до 558; последние цифры для быстроходных судов. Коэффициент δ меняется не только с типом судна, но и с формой лопастей винта: именно, он уменьшается, когда лопасть становится более широкой к концу, чем было принято при опытах для определения δ.

Мощность (индикаторная) N_i, потребная для сообщения судну скорости W (в узлах), определяется по формуле В. И. Афанасьева так:

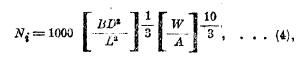
где В и L - наибольшая ширина подводной части судна и длина между перпендикулярами в футах, D — водоизмещение его в тоннах и А — характеристика судна, равная приблизительно 25 для хороших обводов корпуса и правильно подобранного винта.

В. Ветчинкин.