Работа

Работа. В обиходной речи словом: «работа» мы обозначаем различные виды телесной и умственной деятельности, а также результаты этой деятельности, причем вообще не бывает речи, о единой числовой мере работы. Физика дает термину «работа» точный смысл на основании анализа обширной группы процессов, которые с точки зрения обычного словоупотребления соответствуют «совершению работы», или «производству работы». Здесь, прежде всего, обнаруживается, что, например, такой вид работы, как подъем груза, всегда требует наличия некоторой силы, приблизительную оценку которой мы можем произвести при помощи мускульного  чувства. (Точно измерить любую силу можно путем сравнения ее с силой тяжести одного килограмма, т. е. с той силой, с какой килограммовая масса давит — вследствие своей тяжести — на покоящуюся подставку). Но одного наличия силы еще недостаточно для производства работы в физико-механическом смысле. Сила должна быть еще деятельной, т. е. она должна двигать точку своего приложения. В таком случае оказывается, что величина производимой работы тем больше, чем больше работающая сила и чем больше расстояние, пройденное точкой приложения силы по направлению этой последней. На этом основании установлено определение: работа измеряется произведением силы на путь, пройденный по направлению силы. Так, работа поднятия груза измеряется произведением тяжести груза на высоту подъема. Если же мы, например, держим в течение нескольких минут килограммовый груз в горизонтально вытянутой руке, то (с точки зрения физико-механической) работа здесь равна нулю, потому что нет никакого перемещения точки приложения силы. Что же касается непосредственного ощущения, которое говорит нам, что и здесь произведена некоторая работа, сказывающаяся известным утомлением, то оно истолковывается тем, что сократившиеся мышцы производят физиологическую работу, которую нужно выражать не произведением силы на путь, а иначе. Часто применяемой единицей работы является килограмм-метр — работа силы, равной 1 кг, на пути в 1 м; о других единицах работы см. единицы измерений, XIX, 604, приложение.

В теснейшей связи с понятием работы стоит понятие энергии (см.). Всякий раз, как совершается работа, происходит или передача энергии от одного тела другому (например, когда человек поднимает груз, то часть запаса энергии человека передается грузу и принимает форму потенциальной энергии этого последнего), или превращение энергии (например, когда тело падает под действием силы тяжести, то его потенциальная энергия превращается в кинетическую). При этом совершенная работа как раз равняется переданной или превращенной энергии. Это расширенное определение позволяет произвести подсчет работы и в тех случаях, где это было бы невозможно на основании первоначального определения (работа = сила · путь); например, в физиологическом примере сократившейся мышцы, поддерживающей груз, работа равняется затрате энергии мышцей.

Примеры и применения понятия работы

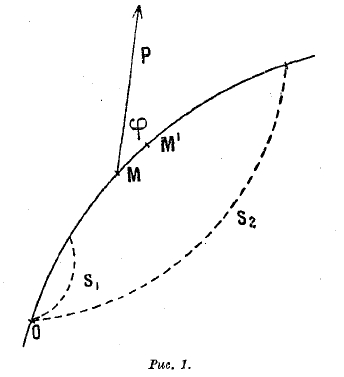
Рис. 1.

1. В общей механике. Если точка приложения М силы Р (рис. 1) проходит исчезающе малый путь MM' = ds, причем φ есть угол, составляемый силой Р и «элементом» пути ММ', то работа силы Р на этом пути равна Pds cosφ; это — так называемая элементарная работа. Если перемещение происходит на конечном пути s₂—s₁ (где s₁ и s₂ — расстояния, отсчитываемые по траектории от начальной точки О), причем сила Р может менять свою величину и направление, то работа на этом пути равна сумме элементарных работ; поэтому она выразится определенным интегралом

Это выражение графически представляется площадью ABCD кривой, изображающей зависимость между проекцией Pcosφ силы Р на касательную к траектории и расстоянием s по траектории от начальной   точки (рис. 2). Заштрихованная полоска представляет элементарную работу.

Весьма важное применение понятия работы — в «принципе возможных перемещений» (см. механика, XXVIII, 576').

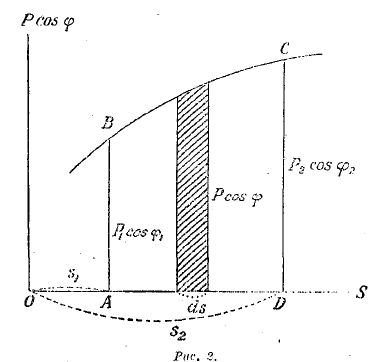
Рис. 2.

2. В теории притяжения (см. тяготение, XLII, 1). Две массы m и m' на расстоянии r притягивают друг друга с силой G(mm’)/r², где G – гравитационная постоянная. Вообразим, что масса m удерживается неподвижно, а масса m' действием некоторой силы, преодолевающей силу тяготения, отодвигается от массы m, так что расстояние r увеличивается на dr. Работа, совершенная при этом, будет G(mm’)/r²dr; эта работа равняется приращению запаса потенциальной энергии системы масс m и m'. Если расстояние r увеличилось на конечную величину R—r (так что в результате рассматриваемого изменения обе массы находятся на расстоянии R), то совершенная работа (или приращение потенциальной энергии системы) будет Gmm' (1/r – 1/R). Если масса m’ = единице массы и если она удаляется на бесконечно большое расстояние от притягивающей массы m (так что В = ∞), то совершаемая работа получает выражение V=G(m/r).

Это выражение называется потенциалом. Итак, потенциал в данной точке «поля тяготения» численно ранен той работе, которую нужно совершить (нередко говорят — «затратить»: подразумевается затрата энергии), чтобы притягиваемую единицу массы из данной точки удалить в бесконечность¹⁾. Это определение сохраняет годность и в том случае, если притягивающих масс не одна, а несколько: m₁, m₂, m₃...; тогда потенциал в точке Q, отстоящей от m₁ на r₁ от m₂ на r₂ и т. д. (рис. 3), будет равен G(m₁/r₁ + m₂/r₂ + …), т. е. он равняется сумме потенциалов, создаваемых в точке Q каждой из притягивающих масс в отдельности. Подсчитать общее действие любой системы притягивающих масс на притягиваемую массу, помещенную в какой-нибудь точке Q «поля тяготения», можно двумя способами: а) складывая геометрически силы, с которыми действует на притягиваемую массу каждая из притягивающих масс, б) исходя из выражения потенциала, создаваемого данной системой масс в точке Q. Второй способ — проще, потому что потенциалы (как выше было указано) складываются арифметически. Этим обусловливается большое значение, которое имеет потенциал в теории притяжения.

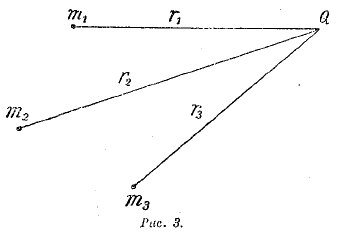
Рас. 3.

3. В теории упругости. Представим себе упругий стержень АВ (рис. 4), закрепленный на одном конце и растягиваемый силой Р, приложенной к другому  концу. Сила Р уравновешивается упругими силами, развиваемыми стержнем. Пусть l — длина стержня до растяжения, σ - его поперечное сечение, λ — удлинение, получаемое им благодаря действию силы работы.

¹⁾ Из данного определения потенциала вытекает, что работы, совершаемая внешнего силой, передвигающей в поле тяготения притягиваемую массу m' из точки 1 в точку 2, равна произведению m' (V₁—V₂) притягиваемой массы на разность потенциалов в этих точках. Работа  действующей в поле силы тяготения при том же перемещении будет раина m’ (V₂—V₁); различие между обоими выражениями обусловлено тем, что внешняя сила по направлению противоположна силе поля.

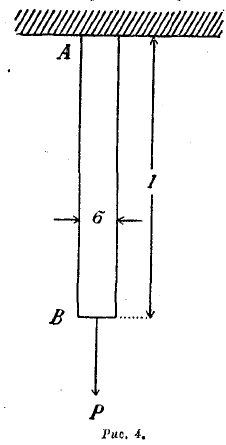
Рис. 4.

Тогда (при небольших удлинениях) λ=Pl/σE, где Е — постоянная величина, характерная для данного вещества и называемая модулем Юнга. Если сила Р увеличивается, начиная от значения Р = 0 и кончая значением Р=Р так, что стержень все время остается в равновесии, то работа этой силы будет

¹⁾ Можно иначе найти этот результат, строя график, аналогичный рис. 2. Зависимость силы Р от пути λ изобразится в данном случае прямой, проходящей через начало координатных осей; ее работа представится площадью прямоугольного треугольника, у которого один катет — окончательное удлинение λ, а другой — окончательное значение силы Р.

 

Эта работа перейдет в упругую энергию стержня. Количество упругой энергии, содержащееся в каждой единице объема растянутого стержня, будет

lP²/2σE : lσ = ½ P²/σ²E = ½ p²/E, где p=P/σ есть «растягивающее усилие» (т. е. сила, приходящаяся на единицу поперечного сечения стержня). Если представить себе, что сила, растягивающая стержень, все время сохраняет постоянное значение Р, то к моменту, когда удлинение сделается равным λ, работа силы Р будет равна Рλ; половина этой работы пойдет на создание упругой энергии ½  Рλ, другая половина превратится в кинетическую энергию частей стержня.

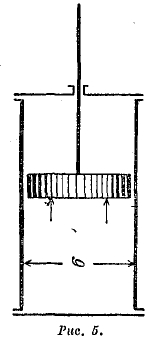
Рис. 5.

4. Работа газообразных тел. Важный пример работы газов и паров дается «рабочим» процессом тепловых двигателей. Газ или пар, заставляя двигаться поршень (рис. 5), производит работу расширения. Если давление внутри цилиндра равно Р, площадь поршня есть σ, то сила, с которой газ или пар действует на поршень, будет рσ; если действием этой силы поршень перемещается на расстояние ds, то совершенная при этом (элементарная) работа будет pσds, или pdv, где dv = σds есть приращение объема v газа или пара при перемещении поршня на ds. Если газ или пар расширяется таким образом от начального объема  до конечного объема v₂ то работа расширения будет

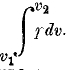
Если на оси абсцисс будем откладывать v, на оси ординат р, то эта работа представится площадью (рис. 6), которая ограничена слева и справа ординатами, соответствующими началу и концу процесса, снизу — отрезком оси абсцисс, сверху — кривой линией, изображающей процесс (т. е. представляющей зависимость между объемом и давлением газа или пара).

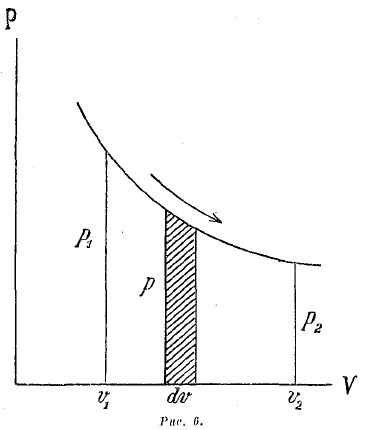
Рис. 6.

Если некоторая внешняя сила заставляет поршень двигаться в обратном направлении, то совершается работы сжатия, которую также можно графически представить площадью. Если процесс является замкнутым или круговым (так что газ или пар, сначала расширявшийся при больших давлениях, затем подвергается сжатию при меньших давлениях, и поршень, сделав ход туда и обратно, возвращается к концу процесса в начальное положение), то полная работа, совершаемая газом или паром за время такого процесса (ABСDA на рис. 7), представится площадью той замкнутой кривой, которая изображает процесс (потому что из работы расширения EABСF нужно вычесть работу сжатия CDAEF). Подобными «диаграммами» весьма часто пользуются при рассмотрении работы тепловых двигателей (см. двигатели внутреннего сгорания, XVIII, приложение; паровые машины, XXXI, 276/80; индикатор, XXI, 616).

Формула работы

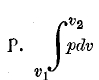
и ее представление остаются верными и тогда, если тело, подвергающееся расширению или сжатию, не заключено в цилиндр, а ограничено произвольной поверхностью (лишь бы только давление р было одинаково во всех точках этой поверхности). Этим обусловливается обширное применение указанной формулы и ее графика в термодинамике.

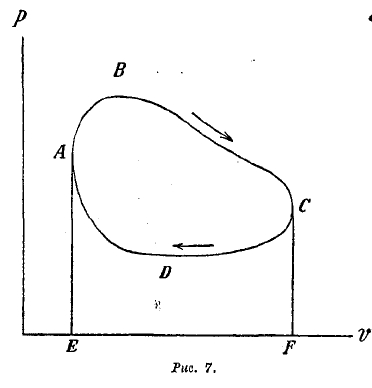
Рис. 7.

5) Работа сил поверхностного натяжения. Предыдущие рассуждения могут быть применены и к жидким телам: расширяясь под действием внешнего давления, жидкость производит работу; сжимаясь, она «поглощает» работу. Но у жидкостей производством или поглощением работы сопровождаются не только изменения объема, но также изменения величины поверхности: чтобы поверхность жидкости увеличивалась, внешние силы должны совершить некоторую работу; наоборот, уменьшая свою поверхность, жидкость производит работу. На рис. 8 изображена проволочная рамочка ABCD с одной подвижной стороной AD, затянутая пленкой из мыльного раствора; пленка, стремясь сократиться, тянет проволочку AD с некоторой силой F кверху; эту тягу можно уравновесить, приложив к проволочке AD силу F по направлению книзу. Если эта сила F получит бесконечно малое приращение, проволочка AD будет двигаться вниз, поверхность пленки будет увеличиваться. Пусть AD переместилась вниз на расстояние а, так что поверхность жидкой пленки увеличилась на 2АD.а (множитель 2 появляется потому, что пленка имеет две стороны — переднюю и заднюю); при этом внешняя сила F совершит работу, равную Fа, эта работа идет на приращение «поверхностной энергии» жидкости¹⁾.

¹⁾ Однако, из этого не следует, что приращение поверхностной энергии равно работе, затраченной извне. Дело в том, что растягиваемая пленка охлаждалась бы, если бы к ней не притекала теплота из окружающей среды; при условии же изотермичности процесса, поглощаемое пленкой тепло также пойдет на увеличение поверхностной энергии.

 

Для данной жидкости при данной температуре сила F, прилагаемая к данному участку AD проволочки, является величиной совершенно определенной (что касается АВ и а, то они могут меняться). Таким образом, имеется пропорциональность между приращением поверхности жидкости и затрачиваемой работы; эта пропорциональность выражается равенством 2AD.аα = Fa, где α = F/2AD есть коэффициент пропорциональности, называемый поверхностным натяжением (см. жидкости, XX, 283). Силы, с которыми пленка стремится сократиться, называются силами поверхностного натяжения.

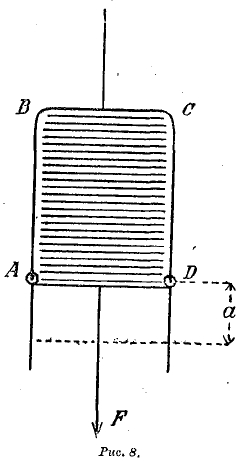
Рис. 8.

6) Работа электрических сил. Под действием электрических сил положительное электричество стремится переходить от высшего потенциала (см. электричество) к низшему, а отрицательное — от низшего к высшему. Если такой переход совершается в действительности, то электрические силы совершают работу, равную произведению q (V₁—V₂) перемещающегося заряда q на разность электрических потенциалов в начале и в конце пути¹⁾.

¹⁾ Существует явная аналогия между электрической работой и работой в поле тяготения (см. выше). Но аналоги эта не полна: электрическая работа выражается через q(V₁-V₂), тогда как работа сил тяготения m’(V₂-V₁): между обоими выражениями – различие в знаке. Это различие обусловлено тем, что весомые массы притягиваются друг к другу, между тем как одноименные электрические заряды отталкивают друг друга.

Измерение работы двигателей производится на практике с помощью динамометров (см. XVIII, 377); измерение электрической работы — с помощью электрических счетчиков.

Мощность. Различные источники работы (например, машины-двигатели) и приспособления, поглощающие работу (например, электрические лампы), сравниваются друг с другом по их «мощности». Так называется работа, производимая (или потребляемая) в одну секунду. Об единицах мощности см. единицы измерений, XIX, приложение 5, 7, 8.

А. Бачинский.