Растворы

Растворы. I. Дисперсные системы. Данное вещество может быть распределено различными способами в другом веществе; первое вещество, находящееся в относительно большем количестве, чем второе, и образующее с макроскопической точки зрения непрерывную среду (фазу), называется дисперсионной средой, или растворителем; второе вещество, находящееся в раздробленном состоянии, частицы которого окружены со всех сторон дисперсионной средой, образует дисперсированную, или растворенную фазу (см. XLV, ч. 2, 335 сл.). Так как оба вещества могут быть в различных агрегатных состояниях, то, очевидно, возможны разные случаи распределения. Обозначим газообразное, жидкое и твердое состояния соответственно буквами Г, Ж и Т; возможными оказываются следующие комбинации дисперсионных (первая буква) и дисперсированных (вторая буква) фаз:

1. Г+ Г  4. Ж+Г  7. Т+Г

2. Г+Ж  5. Ж+Ж  8. Т+Ж

3. Г+Т  6. Ж+Т  9. Т+Т

Необходимо далее провести различие между химическим и физическим определением молекулы (см.). С химической точки зрения молекула — наимень-шее количество однородного вещества, способное химически реагировать; с физической же точки зрения молекулы это отдельные частицы вещества, распределенные в данной среде, они могут совпадать с химической молекулой, но могут, что бывает чаще, представлять собой агрегат химических молекул: физико-химический (например, ассоциированные молекулы, см. XXXII, 492/93) или физический (мельчайшие кусочки вещества, например пылинки). Первая комбинация распределения Г+Г дает один класс смесей, или раствор; это газовые смеси, или раствор газов в газах. Под именем газа мы разумеем собрание химических или физико-химических молекул, распределенных в пустоте; газы смешиваются во всех отношениях (см. ХІI, 306), и их смеси с точки зрения учения о равновесии (см. XLV, ч. 2, 332 сл.) образуют одну газообразную фазу. Вторая комбинация Г+Ж охватывает туманы и газы в момент сжижения; здесь разрозненные частицы в силу жидкой природы обладают шарообразной формой и являются физическими молекулами, могущими состоять из огромного количества химических или физико-химических молекул. Если взвешенные в газе частицы тверды, а, следовательно, в общем случае неправильной формы, то получается третий класс образований Г+Т, например дымы, пыльный воздух. Оба класса, Г+Ж и Г+Т, в зависимости от величины взвешенных частиц, или образуют грубые смеси, в которых частицы заметно не участвуют в броуновском движении (см. VI, 495/97) при обыкновенном давлении и температуре (их часто называют туманами в широком смысле слова), или же образуют аэрозоли с измеримой амплитудой броуновского движения (табачный дым, пары хлористого аммония, туман серной кислоты, цементная пыль, дымовые завесы и т. д.). Аэрозоли в настоящее время являются предметом особо внимательного изучения (см. Б. Гиббс, «Аэрозоли», русский перевод, Лнг. 1929). По мере уменьшения величины взвешенных частиц (увеличения степени дисперсности) оба класса образований делаются все более устойчивыми, а когда их частицы переходят в физико-химические или химические молекулы, то теряется различие между всеми тремя классами, мы получаем смесь паров с газом, или раствор пара в газе, обладающий свойствами первого класса Г + Г. Недостаточно изучены образования с твердой дисперсионной фазой (7, 8 и 9-й классы). К ним принадлежат твердые пены (например, пемза: Т + Г), кристаллы, в частности минералы, с жидкими и твердыми включениями. Если дисперсированная фаза состоит из очень малых частиц, то такие образования называются твердыми растворами, например рубиновое стекло, в котором дисперсированной фазой является золото, ультрамарин, которому распыленная сера сообщает синий цвет, далее опал, аметист и т. п. В предельном случае, когда распыленные частицы имеют размеры обыкновенных молекул, мы получаем настоящие твердые растворы, в частности смешанные кристаллы (ср. XXV, 597/98, и ХХVІІI, 688/89). Наилучше изучены образования с жидкой дисперсионной фазой, особенно комбинации Ж+Ж и Ж+Т. К классу Ж+Г принадлежат пены различной степени дисперсности. Когда газ молекулярно дисперсирован, получаем обыкновенный раствор газа в жидкости. Особо важными являются комбинации Ж+Ж и Ж+Т. Если взвешенные частицы достаточно велики, то получаются грубо дисперсированные системы, при первой комбинации называемые эмульсиями (например, эмульсии масел в воде), при второй — суспензиями (например, взвесь глины в воде). Если дисперсированная фаза состоит из очень малых частиц, но в общем случае больших, чем химические или физико-химические молекулы, то получаем коллоидные растворы. Хотя в таких растворах частицы часто бывают так малы, что трудно говорить об их агрегатном состоянии, их все-таки иногда делят на основании аналогии со свойствами эмульсий и суспензий на эмульсоиды и суспенсоиды. Наконец, когда взвешенными частицами являются химические или физико-химические молекулы, мы имеем дело во всех трех комбинациях с обыкновенными растворами. Между тремя группами, грубо-, высоко-дисперсированными системами и обыкновенными растворами, имеются непрерывные переходы. Итак, термин «раствор» применяется к молекулярно-дисперсированным системам (обыкновенные растворы, если дисперсионная среда — жидкость, твердые растворы, если дисперсионная среда — твердая), к высокодисперсированным системам при жидкой дисперсионной среде (коллоидные растворы) и иногда к смесям газов (паров).

В дисперсных и в молекулярно-дисперсированных системах мы имеем дело с двоякого рода молекулами — растворителя и растворенного вещества. В растворителе всегда имеются или химические, или физико-химические молекулы, растворенное же вещество, или в общем случае дисперсированное, может быть или в виде тех же молекул, или в виде физических молекул, агрегатов подчас огромного количества обыкновенных молекул. Такие частицы в дисперсных системах играют роль молекул, что доказывается общностью некоторых явлений у всех дисперсных систем. Такими общими явлениями оказываются распределение концентраций в дисперсоидах с высотой и характер движения молекул (частиц) их.

Под концентрацией мы разумеем количество растворенного (дисперсированного) вещества в единице объема раствора (дисперсоида); это количество может быть определено также числом молекул или частиц. Лаплас дал гипсометрическую формулу, показывающую, как падает давление газа с высотой. Оказывается, что давления р₀, р₁, р₂, р₃,... на разных высотах, равноотстоящих друг от друга, относятся между собой, как числа, образующие геометрический ряд р0:р1:р2:р3… = а:а.2:а.2²:а.2³... Поскольку давления газа пропорциональны числам молекул в соответствующих слоях на разных высотах, в данной формуле мы можем вместо давлений подставить, числа молекул. Если действительно видимые под обыкновенным микроскопом частицы в грубых суспензиях и эмульсиях играют роль физических молекул, то к ним должна быть применима формула Лапласа. Опыты Перрена с эмульсией краски гуммигута в воде вполне подтвердили это предположение (см. брауново движение). Оказалось, что эти шарики располагаются на разных высотах по тому же закону, что и молекулы газа. В столбе чистого водорода надо подняться на высоту в 80 км, чтобы наблюдать половинное давление. В столбе кислорода давление падает наполовину на высоте 5 км, а в случае воздуха — на высоте в 6 км. В эмульсии гуммигута с шариками радиуса в 0,212 μ надо подняться на 30 μ, чтобы в горизонтальном слое число частиц равнялось половине числа частиц на дне. При радиусе шариков в 0,52 μ достаточно подняться на 6 μ. Нетрудно вычислить, что в таком случае средняя молекула воздуха должна составлять 10^—9 часть шарика (физической молекулы) гуммигута в воде. Очевидно, что в смеси газов с высотой будет изменяться и состав смеси, более тяжелые молекулы будут скучиваться в нижних слоях. Так, в случае воздуха на высоте в 80 км, где давление падает до 0,0192 мм, имеется кислорода только 1%. Понятно, что и в обыкновенных растворах при условии очень высоких столбов их концентрация будет следовать той же формуле Лапласа. Значения соответствующих высот будут определяться размерами молекул растворенного вещества, а так как последние того же порядка, что и газовые молекулы, то и высоты должны измеряться километрами. Коллоидные растворы дают в этом отношении промежуточные значения между эмульсиями и обыкновенными растворами.

В газах молекулы находятся в непрерывном движении (см. ХII, 315/17); при обычных температурах и давлениях средний свободный путь молекул в газе превышает их диаметр приблизительно раз в триста, число столкновений молекулы с другими в секунду огромно, около 10⁹. В случае жидкости, размеры расстояний между молекулами того же порядка, что и размеры их диаметров, эти молекулы также находятся в постоянном движении и испытывают весьма частые столкновения (см. XX, 279). Если в жидкости, скажем воды, находятся частицы много большие, чем молекулы воды, то такие частицы испытывают удары молекул воды одновременно с разных сторон; поскольку движения молекул воды беспорядочны, результаты ударов их в частицу могут уравновешиваться со статистической точки зрения в случае огромного количества ударов. Если же частицы недостаточно велики, то они под влиянием неуравновешивающихся ударов со стороны молекул воды будут беспорядочно двигаться; такое движение называется броуновским движением (см. брауново движение). Наблюдаемое нами броуновское движение частиц в жидкости, превышающих размеры молекул последней, действительно является результатом молекулярного движения в жидкости; оно так же, как и молекулярное движение, вечно и беспорядочно. Теория этого движения, данная Эйнштейном и Смолуховским, вполне подтверждена была опытами Перрена с эмульсиями разных веществ, в частности гуммигута. Эта теория приводит к определению подвижности броуновского движения, в формулу же для подвижности входят наряду с другими величинами газовая постоянная и авогадрово число N (число молекул в грамм-молекуле вещества); путем изучения броуновского движения в эмульсиях Перрен определил численное значением оно оказалось равным в среднем 6,4.10²³. Этими опытами, подтвержденными рядом других исследований доказано, что дисперсоиды и обыкновенные растворы представляют образования одного и того же рода; в дисперсоидах даже видимые под микроскопом частицы играют роль молекул. Зная вес таких частиц, скажем, в эмульсии и умножив его на число N, мы найдем грамм-молекулярный вес того комплекса, который в эмульсиях играет роль молекул растворенного вещества; в эмульсиях он оказывается равным миллионам килограммов. Таким образом, одни и те же законы приложимы к веществам, грамм-молекула которых изменяется от 2 г до миллионов килограммов. Молекулы вследствие взаимных столкновений не только постоянно изменяют величину и направление своего поступательного движения, но и приходят в беспорядочное вращательное движение. Вращаются так же и большие частицы в дисперсоидах; броуновскоо вращательное движение изучено теоретически и экспериментально и еще раз подтверждает правильность концепции об общности свойств дисперсоидов и обыкновенных растворов. Ряд и других свойств растворов, являющихся функциями величин молекул, оказывается общим для всех дисперсных систем; только подход к их изучению должен быть различным в зависимости от величины молекул растворенного (дисперсированного) вещества. К таким свойствам относятся диффузия (см.), диализ, фильтрация окраска и т. д.

II. Обыкновенные растворы. В таких растворах размеры молекул растворителя и растворенного вещества — одного порядка и колеблются от 0,1 до 1—1,5 μμ. Подход к изучению свойств обыкновенных растворов троякий: эмпирический, термодинамический и кинетический. Эмпирическое изучение растворов дает не только огромное количество фактов и численных значений свойств растворов, но и пытается дать связь и зависимость между ними.

1) Смеси газов (паров) по существу принадлежат к обыкновенным растворам, хотя этот термин не всегда применяется к ним. Во многих отношениях смеси газов обладают теми же свойствами, что и отдельные газы (см.), но имеется ряд свойств, характерных для смесей, особенно в критической области (см. критическое состояние). Самообразование смеси (раствора) газов сопровождается увеличением энтропии. В теории этих смесей мы исходим из определения, согласно которому свободная энергия смеси газов при данной температуре и объеме равна сумме свободных энергий компонентов смеси, взятых в объеме смеси при той же температуре. Из этого определения и термодинамики вытекает стройный ряд следствий, оправдываемых опытом и охватывающих все свойства смесей газов. В случае реальных газов мы наблюдаем ряд особенностей, не имеющихся в отдельных газах, особенно при сжижении их достаточно сказать, что в бинарных смесях имеются две критические точки: одна, отвечающая концентрации смеси, выше которой все смеси находятся в газовом состоянии, а ниже — в жидком; другая, в которой исчезает различие между газовым и жидким состоянием. Существование двух критических точек влечет за собой своеобразные явления в области конденсации; так, например, имеются случаи, когда увеличение давления (при постоянной температуре) на жидкую смесь вызывает образование парообразной фазы.

Изучение смесей газов составляет задачу термодинамики, для теории же растворов такие смеси представляют огромный интерес в критической области, в каковой другие растворы почти не изучались: ценность этого отдела термодинамики для общего учения о растворах скажется в будущем.

2) Растворы в жидком растворителе — растворы в узком смысле слова — делятся на три группы: растворы газов, жидкостей и твердых веществ (см. жидкости, XX, 286/91). Особо важным моментом здесь является представление о насыщенности растворов. Обозначим два вещества через А и В; если оба они — жидкости, то могут быть случаи, когда А и В смешиваются во всех отношениях, и тогда мы говорим о растворах вещества В в А, если последнего в смеси много больше, чем первого, или о растворе вещества А в В в обратном случае; если в смесях количество А и В одного порядка, мы говорим просто о их смеси. Если А — жидкость, а В — газ или твердое вещество, то имеется предел растворимости В в А, и можно говорить только о растворе В в А; предел растворимости часто имеется и в том случае, если и В — жидкость: это случаи несмешивающихся жидкостей — например, воды и эфира, воды и бензола и т. п. В общем случае здесь мы имеем для каждой пары жидкостей два предела растворимости: В в А и А в В; между этими пределами лежит гетерогенная область двух жидких несмешивающихся слоев, каждый из которых является насыщенным раствором одной жидкости в другой.

Раствор  называется насыщенным, если его концентрация при данной температуре не изменяется в присутствии излишка растворенного вещества, другими словами, если он находится в равновесии с другой фазой (газовой, жидкой, твердой). Явление насыщенности растворов обусловливает существование трех видов растворов — ненасыщенного, насыщенного и пересыщенного; последний может иметь место только в отсутствии второй фазы, состоящей из растворяемого вещества, пересыщенные растворы — неустойчивы, и часто достаточно ничтожного количества (пылинки) растворенного вещества, чтобы уничтожить пересыщенность и вызвать выделение во вторую фазу излишка растворенного вещества. Явление пересыщенности играет видную роль в природе и в технике, но планомерно не исследовано. В дальнейшем мы будем говорить только о насыщенных и ненасыщенных растворах.

а) В области растворов газов в жидкостях (см. XII, 314) мы имеем основной закон Генри: «Растворимость газа в жидкости при данной температуре пропорциональна давлению»: с=ар, где с — концентрация газа в жидкости, р — давление его, а — коэффициент пропорциональности. О растворах газов можно говорить только при наличии двух фаз: жидкой — раствор и газовой (смесь газа и пара растворителя). Пусть в растворе имеется n₁ молей (грамм-молекул) растворителя и n₂ молей растворенного газа, тогда концентрация последнего N₂ = n₂/(n₁+n₂) (по определению); если парциальное давление газа в газовой фазе обозначим через р₂, то закон Генри может быть переписан так:

р₂ = kN₂ (1).

Коэффициент эмпирический, но можно дать ему физическое толкование: это — упругость пара р₂° сжиженного газа, если бы он был удержан в жидком состоянии выше своей критической температуры; значение р₂° может быть найдено путем экстраполирования упругостей сжиженного газа. В таком случае из (1) получим

N2 = р²/р₂° (2),

из последнего же выражения сразу вытекают следующие следствия:

(а) При данной температуре и данном парциальном давлении газ одинаково растворим во всех растворителях, так как характер растворителя не входит в выражение р²/р₂°; пример: растворимость азота в бензоле 4,1, в хлороформе 4,3.

(b) Газ с высшей критической температурой более растворим, чем газ с низшей критической температурой.

Присоединив к данному закону теорему Клаузиуса-Клапейрона¹⁾, найдем, что

(с) растворимость газа с увеличением температуры падает.

¹⁾ Теорема Клаузиуса-Клапейрона, — результат приложения первых двух принципов термодинамики к взаимным превращениям фаз, — дает связь между возрастанием упругости системы с температурой (dp/dT), теплотой превращения одной фазы в другую (L) и разницей между удельными объемами двух фаз (v₂—v₁) при заданной температуре Т:

dp/dT = L/(v₂-v₁)T

Если первая фаза находится и жидком или твердом состоянии, а вторая — парообразна, то при температурах, далеких от критической, удельным объемом первой фазы можно пренебречь по сравнению с удельным объемом второй фазы (например, для воды при 100°С v₁ = 1 см³, v₂ = 1674 см³), тогда dp/dT = L/v²T; если, далее, применить газовый закон pv=RT к парам, то уравнение Клаузиуса-Клапейрона примет форму:

dp/dT = Lр/RT² или dlnр/dT = L/RT²

от этой дифференциальной формы можно перейти к интегральной:

ln(p₂/p₁) = L/R (1/T₁-1/T₂)

где R — газовая постоянная, а р₁ и р₂ — упругости пара системы при абсолютных температурах Т₁ и Т₂.

 

Растворы  газов, подчиняющиеся закону Генри, особенно в форме (2), называются идеальными растворами (ср. XII, 306). Реальные растворы уклоняются, подчас очень сильно (аммиак), от этого закона, о причинах уклонений см. ниже.

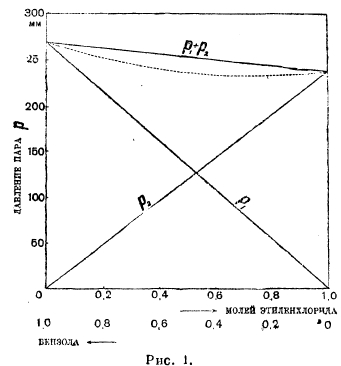
Рис. 1.

b) Раствор жидкостей в жидкостях. Общий случай — смешиваемость жидкостей во всех отношениях (см. XX, 289); так как обе жидкости обладают упругостями паров, то исходным пунктом в их изучении являются взаимоотношения между составом жидкой фазы и парциальными давлениями компонентов в парообразной фазе. Пусть количества молей в растворе первой жидкости n₁ второй n₂ тогда молярная концентрация первой жидкости

N₁ = n₁/(n₁+n₂), второй N₂ = n₂/(n₁+n₂). Пусть упругость пара первой жидкости (при данной температуре) р₁°, после растворения в ней n₂ молей второй жидкости упругость пара первой уменьшится до р₁; выражение (р₁°-р₁)/ р₁° называется относительным понижением упругости пара первой жидкости; по эмпирическому закону Рауля

(р₁°-р₁)/ р₁° = n₂/(n₁+n₂)

или после небольшого преобразования

р₁ = р₁° n₁/(n₁+n₂) = р₁° N₁… (3).

Аналогично найдем для второй жидкости

Р₂ = Р₂° N₂… (4)

Закон Рауля в форме (3) и (4) может быть положен в основу изучения всех растворов, причем те из них, которые строго подчиняются этому закону, называются идеальными. Закон Рауля есть частный случай закона Генри (1), в котором k — эмпирический коэффициент. Форма закона Генри (2) объединяет обе группы растворов. Нетрудно сообразить, что закон растворов может быть распространен на смеси или растворы нескольких веществ.

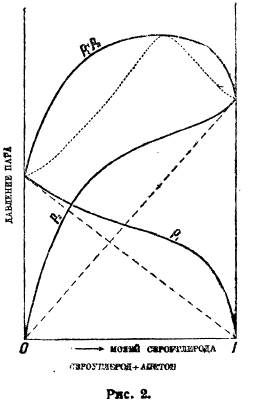
Рис. 2.

На рис. 1 на оси абсцисс отложены молярные концентрации обоих компонентов в жидкой фазе, на оси ординат упругости паров: парциальные р₁ и р₂ и полная р₁ + р₂. В идеальных растворах все три зависимости упругостей от состава линейны. Такую картину дают, например, смеси бензола и этиленхлорида. В других случаях мы имеем уклонения от линейного хода этих кривых, т. е. уклонения от закона Рауля. Мы имеем два главных типа уклонений: рис. 2 показывает положительные уклонения, рис. 3 — отрицательные. На рисунках показаны непрерывными кривыми реальные зависимости парциальных и полных упругостей от состава смеси, прерывными — идеальный ход, требуемый законом Рауля. Рис. 2 отвечает смесям сероуглерода и ацетона, рис. 3 — ацетона и хлороформа. Смешанные типы — очень редки. Очень характерно течение кривых парциальных давлений в верхней части (линейная часть), свойственное только не электролитам.

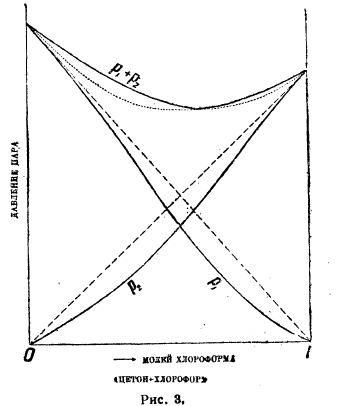
Рис. 3.

Для учета уклонений берут ln(p₁/p₁°N₁) и, разлагая его в ряд Маргулеса, связывают с уравнением Дюгема,  в результате чего вытекает ряд ценных правил и формул; такое уклонение в логарифмической форме может быть приравнено выражению ½βN₂, где β – коэффициент пропорциональности. При высших значениях кривые уклонений получают S-образный вид (рис. 4)  - это отвечает расслоению смеси на два жидких слоя (состава А и С на рис. 4). При некотором значении β возможна касательная, параллельная оси абсцисс, такой случай отвечает критической температуре смесей двух жидкостей.

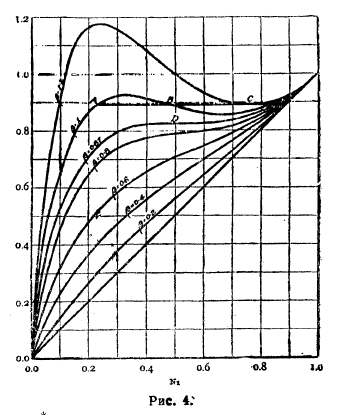
Рис. 4.

Общий случай расслоения смесей показан на рис. 5 (никотин+вода) с нижней (60°) и верхней 210° критическими температурами: ниже 60° и выше 210° никотин и вода смешиваются во всех отношениях, между этими же температурами образуются два несмешивающиеся раствора: раствор никотина в воде и раствор воды в никотине. Более частыми случаями являются смеси с одной верхней критической температурой, где, чем ниже температура, тем резче выражено расслоение (например, вода и анилин, критическая температура 167°), менее часты случаи с одной нижней критической температурой (например, вода и триэтиламин, критическая температура 18,6°). Наконец, многочисленны случаи, когда критическая температура расслоения лежит выше критической температуры превращения жидкости в пар, очевидно тогда нет такой температуры, при которой бы две данные жидкости смешивались во всех отношениях (примеры: вода + эфир, вода + бензол, вода + хлороформ и др.). Два жидких раствора, не смешивающиеся между собой, образуют одну и ту же парообразную фазу, т. е. два раствора весьма разного состава образуют пар одного и того же состава.

Закон Рауля, положенный в основу эмпирического изучения растворов, ценен тем, что уклонения от него могут быть сопоставлены с рядом других свойств растворов и что такое сопоставление приводит к большому ряду правил и законов, общих всем растворам и дает ценные указания  на внутренние свойства веществ в жидком состоянии. Так как эти обобщения справедливы и для растворов твердых веществ в жидких растворителях, то, прежде чем переходить к обобщениям, надо ознакомиться с приложением закона Рауля к таким растворам.

Рис. 5.

с) Растворы твердых веществ в жидкостях. На рис. 6 по оси абсцисс отложены молярные концентрации растворенного (твердого вещества) от N₂=0 до N₂ = 1, в последней точке мы представляем себе растворяемое вещество в жидком состоянии при данной температуре. Диагональная прямая есть кривая парциальной упругости этого вещества в растворе; мы полагаем, что, как бы мала ни была эта упругость, она все же имеется. Здесь р₂° — упругость изучаемого вещества, если бы оно было при данной температуре в расплавленном состоянии, р₂^s — упругость пара его в твердом состоянии; так как р₂^s всегда меньше р₂° (ибо расплавленное состояние при данной температуре неустойчиво), то растворимость твердого вещества должна быть ограниченной, как это видно из рис. 6:

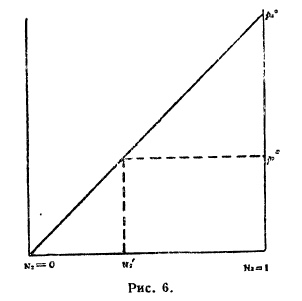
Рис. 6.

насыщенным будет раствор состава N₂’, у которого парциальная упругость растворенного вещества равна упругости его в твердом состоянии р₂^s; насыщение наступит при р₂ = р₂^s  тогда по (4)

N₂’ = р₂^s/ р₂°

Применив к данному случаю термодинамическую теорему Клаузиуса-Клапейрона, найдем замечательную формулу

Ln N₂’ = -L/R (1/T – 1/T_m),

где L — теплота плавления растворяемого вещества; Т_m — абсолютная температура его плавления; Т — заданная температура, R — газовая постоянная. Из этой формулы непосредственно вытекают следующие правила.

α) Растворимость твердого вещества тем больше, чем выше температура (см. XX, 287/88); редкие обратные случаи — результат уклонений от закона Рауля.

β) Твердое вещество с высшей температурой плавления менее растворимо, чем вещество с низшей температурой плавления.

γ) Если два твердых вещества имеют одинаковую температуру плавления, то менее растворимо то, у которого теплота плавления больше.

d) Обобщения. Известно, что растворение сопровождается тепловым эффектом (см. термохимия, XLI, ч. 7, 570/71) и что объем раствора не равен сумме объемов компонентов его (см. XX, 288).

Сопоставление этих фактов с законом Рауля приводит к следующим правилам. Если раствор подчиняется закону Рауля в широких пределах температуры и давлений, то теплота смешения двух жидкостей равна нулю, а в случае растворения твердого вещества теплота растворения равна теплоте его плавления (с поправкой на изменение этой теплоты с температурой), объем же раствора равен сумме объемов компонентов в жидком состоянии. В случае положительных уклонений от закона Рауля наблюдается расширение раствора, что же касается теплоты, то при смешении двух жидкостей наблюдается поглощение теплоты, а в случае твердого вещества теплота растворения (поглощение тепла) больше теплоты плавления; при отрицательных уклонениях — обратно. Уклонения от закона Рауля влияют и на величину растворимости: а именно, у газов и твердых веществ положительные уклонения отвечают меньшей растворимости, а отрицательные — большей, чем в случае идеального поведения. Весьма важным моментом в учении о растворах является выяснение причин уклонений растворов от закона Рауля; таких причин много: внутреннее давление жидкостей, образование химических соединений в смесях (например, амальгамы), ассоциация компонентов, полярность их и, наконец, сольватация. Эти причины тесно связаны друг с другом, сопоставление их с законом Рауля приводит к ряду восьми ценных выводов; правда, что такое изучение растворов ново и что только в будущем можно ожидать цельной картины. Равенство внутренних давлений смешиваемых веществ является условием подчинения их смесей закону Рауля. Различия внутренних давлений и ассоциация молекул ведут к положительным уклонениям, тенденция к образованию химических соединений и полярность — к отрицательным уклонениям. Особый интерес представляет полярность веществ; у неполярных (нормальных) веществ поле сил вокруг молекул симметрично, у полярных (ненормальных) оно несимметрично, вследствие чего такие молекулы сильнее притягиваются и тем вызывают повышенные кохезию (сцепление), поверхностное напряжение, внутреннее давление, теплоту испарения и т. п.; такие жидкости являются растворителями электролитов (вода, аммиак, серная кислота, расплавленные соли и др.). В группе растворов ненормальных веществ видную роль играют растворы электролитов (см. электрохимия). Сольватация состоит в том, что вокруг молекулы растворенного вещества группируются молекулы растворителя более тесно, чем в массе жидкости; такой комплекс не имеет резкой границы и на периферии постепенно переходит к обычным условиям в данной жидкости; сольватация возникает в силу ненормального притяжения между разными молекулами и влечет собой отрицательные уклонения от закона растворов; понятно, что явление сольватации очень часто наблюдается при смешении веществ с высокой полярностью. Если растворителем является вода, то вместо сольватации говорят о гидратации. Учение о сольватации берет начало в теории растворов Д. И. Менделеева, который считал, что в водных растворах мы имеем дело с определенными гидратами (см.) в состоянии диссоциации. Поскольку сольватация и полярность приводят подчас к резким отрицательным уклонениям раствор от закона Рауля, становится понятным, почему в случае электролитов процессы ионизации и coльвaтaции вызывают увеличение растворимости и приводят часто к ненормально высоким растворимостям. Необходимо отметить, что современное эмпирическое учение о растворах, положив в основу закон Рауля, не ограничивается качественными выводами, а пытается дать (часто успешно) и количественный учет явлений; особенность этого учения – охват  всех растворов независимо от агрегатного состояния растворимого вещества и от концентрации их, широкое использование термодинамики и внесение новых понятий.

Такими новыми понятиями являются летучесть (fugacity) вещества и активность его. Летучесть —  это мера стремления компонента уйти из данной среды (фазы); она равна давлению в случае идеального газа, в реальных случаях она есть исправленное давление и может быть определена из отношения f/P = P/P_i , где f — летучесть, P — реальное давление, Р_i — давление, вычисленное из газового закона P_i = RT/v. Положив в основу понятие летучести, мы должны писать закон Рауля так:

f₁ = f₁⁰N₁, f₂ = f₂⁰N₂, …

Активность — это эффективная концентрация вещества в системе, она совпадает с аналитической в пределе; она определяется отношением

a₁ = f₁/f₁⁰, a₂ = f₂/f₂⁰…

Отсюда закон Рауля может быть формулирован так: a₁ = N₁, a₂ = N₂…

Исторически учение о растворах развилось из изучения растворов нелетучих твердых веществ. У этих растворов был открыт закон Рауля, на свойствах их же основано учение вант-Гоффа. Последний обратил особое внимание на осмотическое давление, рельефно проявляющееся, если водный раствор нелетучего вещества в сосуде, нижняя часть которого состоит из полупроницаемой перепонки (пергамента, пузыря или искусственной перепонки, см. XX, 290), погрузить в чистую воду. Вода проникает в сосуд, и жидкость в трубке поднимается вверх до некоторого предела; гидростатическое давление столба жидкости уравновешивает и измеряет ту силу, названную осмотическим давлением, которая вталкивает воду через перепонку внутрь раствора. Осмотические давления растворов, содержащих 0,1 и 1,0 гр./молекулу тростникового сахара в 1 000 г воды при 0°, равны соответственно 2,42 и 24,45 атм. Вант-Гофф показал, что это давление в пределах ошибок опытов (старых) подчиняется закону Бойля, т. е. что оно пропорционально концентрации раствора, закону Гей-Люссака, т. е. что коэффициент возрастания давления на каждый градус повышения температуры равен 1/273 и закону Авогадро, — другими словами, он показал, что осмотическое давление равно тому газовому, которое проявлялось бы, если бы растворенное вещество находилось в объеме раствора в газовом состоянии при данной температуре; в этом случае основным уравнением раствора является уравнение, по внешности тождественное с газовым, πv = n₂RT, в котором n — осмотическое давление, v — объем раствора, R — газовая постоянная, Т — абсолютная температура, n₂ — число гр./молекул растворенного вещества. После того, как удалось связать осмотическое давление с рядом других свойств раствора, в том числе с законом Рауля, и удалось с помощью понятия об осмотическом давлении вывести формулы для повышения точки кипения и понижения точки замерзания раствора, имеющие большое практическое значение для определения молекулярного веса растворенных веществ, учение об осмотическом давлении заняло центральное место в формирующейся в то время физической химии. Вначале смущающим моментом была неприменимость этого учения к растворам электролитов: у последних осмотическое давление было значительно выше вычисляемого. Но после того как Аррениус дал свою теорию электролитической диссоциации, согласно которой электролиты в растворах распадаются на ионы, растворы электролитов не только подкрепили теорию вант-Гоффа, но и создали ей одно из лучших оснований. Оба учения, вант-Гоффа и Аррениуса, тесно сплелись (см. электрохимия.) и на долгие годы определили развитие физической химии в данной области.

Газовое давление — результат бомбардировки молекулами газа стенок сосуда. Что же представляет собой с кинетической точки зрения осмотическое давление? Простейшие представления не выдерживают критики, и только в последнее время Эйнштейну удалось нарисовать сложную картину, в результате которой удары молекул растворенного вещества о перепонку и участие в явлении молекул растворителя приводят к кинетическому пониманию осмотического давления. Позднейшие опыты Морзе, Фрезера, Берклея и Гартлея и др. точных измерений осмотического давления показали, что между газовым и осмотическим давлениями нет тождества и что они тем ближе, чем разведеннее раствор. Дальнейшие исследования показали, что переход к концентрированным растворам и охват всех растворов с точки зрения осмотического давления невозможен.

Критика учения об осмотическом давлении и его кинетического толкования была начата со стороны чистой термодинамики (ван-Лаар, ван-дер-Ваальс); она показала, что осмотическое давление является одним из равноправных свойств растворов и что оно не годится в качестве обобщающего начала. Термодинамика положила в основу учения о растворах понятие о химическом потенциале и привела к весьма обобщенному уравнению, охватывающему в дифференциальной форме все бинарные двухфазные системы. Для того чтобы термодинамически подойти к осмотическому давлению, надо уклониться в сторону и выводить уравнение независимо от только что указанного обобщенного уравнения; этот факт отвечает тому, что осмотическое давление имеет место только при наличии особых условий: раствора и растворителя, разделенных перепонкой; об осмотическом давлении раствора самого по себе говорить нельзя. Термодинамика приводит к следующей формуле для осмотического давления:

πv = -RT ln (l-N₂); если разложим In в ряд и отбросим все высшие члены ряда, то

(N₂ = n₂/(n₁+n₂), n₁+n₂ = 1, N₂=n₂) получим формулу вант-Гоффа. С термодинамической точки зрения нет тождества между газовым и осмотическим давлением, имеется совпадение формул в предельных случаях.

Если по одну сторону перепонки находится растворитель, по другую — раствор, то химический потенциал растворителя по обе стороны перепонки не одинаков, так как со стороны раствор к единице поверхности перепонки прилегает меньшее число молекул растворителя (часть места занята молекулами растворенного вещества), чем со стороны чистого растворителя. Равновесие наступит тогда, когда этот потенциал по обе стороны перепонки будет одинаковым, вследствие чего растворитель будет входить в раствор до тех пор, пока гидростатическое давление, равное осмотическому, в растворt не уплотнит молекулы так, что по обе стороны перепонки на единицу площади числа молекул растворителя станут одинаковыми.

Обобщенное уравнение, пригодное для всех двухфазных бинарных систем, к сожалению, для своего использования требует знания уравнения состояния смеси двух веществ, между тем как нам неизвестно точное уравнение состояния и для индивидуального вещества. Во всяком случае, попытка ванн-дер-Ваальса дать такое уравнение для смесей двух веществ и использование его в указанном выше смысле дало очень много ценного материала, хотя и в мало доступной форме. Новое учение Льюиса и Гильдебранта, вернувшееся к эмпирическому источнику (закону Рауля), уже тесно связанное с термодинамикой, имеет полную возможность широко использовать пути, указанные ван-дер-Ваальсом. В синтезе этих двух учений надо видеть ближайшее будущее учения о растворах.

Термодинамический подход к растворам шире охватывает вопрос; так,  например, он ставит и решает вопрос о взаимоотношениях между составами жидкой фазы (раствор) и парообразной. Как правило, состав жидкого раствора отличен от состава пара, находящегося в равновесии с ним. Мы получаем две кривые полной упругости пара, если станем относить ее один раз к составу жидкой фазы, другой раз к составу пара. На рис. 7 кривая abc отмечает упругости пара взаимных растворимых веществ А и В, отвечающих данным составам жидких растворов, кривая же adc — те же упругости, если на оси абсцисс нанесен состав пара. Раствор  и его пар в равновесии обладают одинаковым давлением (например, прямая fc), следовательно, жидкому раствору состава h отвечает пар состава g. Из этой двойственности кривых упругости пара вытекает большой ряд следствий, имеющих огромное практическое значение: так, вся теория и практика перегонок жидких  смесей основана на этом явлении (см. фракционированная перегонка). В тех случаях, когда раствор подчиняются закону Рауля, первая кривая — прямая, вторая —  гипербола (рис. 1). Положительные уклонения от закона Рауля могут дать кривые, проходящие через максимум давления (рис. 2), а отрицательные — через минимум (рис. 3). По закону Гиббса-Коновалова, обе кривые имеют общую точку в экстремумах, следовательно, только в этих точках состав пара и жидкости одинаков; смеси, отвечающие при данной температуре экстремуму давления или при данном давлении (например, 1 атм.) экстремуму точки кипения, называются нераздельно кипящими, так как перегоняются в одной температурной точке и ведут себя как индивидуальные вещества. Однако, нераздельнокипящие смеси не являются химическими соединениями, так как с изменением давления непрерывно изменяется их состав.

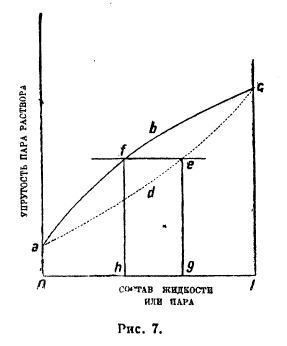
Рис. 7.

Такие явления мы наблюдаем и в более сложных тройных смесях; изучение их привело к новым способам технического получения чистых веществ (например, абсолютного спирта). Эта глава учения о растворах получила название ацеотропизма. В качестве примеров можно указать на раствор этилового спирта и воды. При 1 атм. спирт кипит при 78,30°, вода при 100°, смесь, содержащая 95,57% спирта по весу кипит при 78,15°; никакой перегонкой спиртсодержащей жидкости нельзя получить спирта крепче 95,57% по весу. Поскольку полярные вещества в растворах показывают отрицательные уклонения от закона Рауля, они часто дают резко выраженные максимумы точек кипения (минимумы упругостей пара); так, при 1 атм. вода кипит при 100°, хлористый водород — НСІ при 85°, раствор же в воде, содержащий 20,2% НСІ, кипит при 110° и перегоняется без изменения.

Когда два раствора двух веществ не смешиваются друг с другом, то картина взаимоотношений между ними и общим паром сложнее; изучение таких случаев очень ценно и с теоретической и с практической точки зрения; так, например, оно дает обоснование перегонок с паром.

Разведенные растворы. Часто, когда говорят о теории растворов, понимают узкую область разведенных растворов нелетучих веществ, а иногда даже только растворы электролитов. Действительно, первые теоретические исследования были сделаны в области разведенных растворов; наличие очень слабых концентраций позволяет ввести много упрощений и придти таким образом к простым закономерностям. Сама концентрация N₂ = n₂/(n₁+n₂) при очень малом n₂ в сравнении с количеством n₁ растворителя может быть представлена в виде N₂ = n2/n₁, а закон Рауля в виде p⁰-p/p⁰ = n₂/n₁ или Δp/p⁰ = N₂; если навеска и молекулярный вес растворителя g и М₁, а растворенного вещества g и М₂, то n₁ = g/M₁, n₂ = g/M₂, а тогда из закона Рауля следует, что молекулярный вес растворенного вещества М₂ = p⁰/Δp · gM₁/g; эта формула позволяет определять молекулярный вес растворимых веществ. Воспользовавшись теоремой Клазиуса-Клапейрона, можно заменить понижение упругости пара раствора понижением температуры его замерзания или повышением температуры его кипения (см. криоскопия, ХXV, 626, и эбулиоскопия). Полная термодинамическая теория разведенных растворов была дана Планком.

О вопросах, относящихся к ионизации растворов (электролитическая диссоциация) см. электрохимия.

Твердые растворы. Молекулярное распределение одного вещества в другом в твердом состоянии ведет к понятию о твердых растворах. Если ограничить термин «твердый» кристаллическим состоянием, то твердые растворы совпадают с изоморфными смесями (см. XXV, 598, 613 сл.). Если условиться называть также твердым состоянием состояние очень вязких переохлажденных жидкостей, например, стекла (ср. XLI, ч. 7, 290/92), то понятие твердых растворов будет шире понятия об изоморфных смесях. С термодинамической точки зрения все то, что говорится о бинарных жидких смесях, может быть перенесено и на твердые растворы. Существенная разница между жидкими и твердыми растворами лежит в кристаллографическом строении последних (см. кристаллическая структура, кристаллография, сплавы).

III. Коллоидные растворы (золи). В таких растворах частицы растворенного вещества, играющие роль физических молекул, обладают размерами от 1 μμ до 0,1 μ; понятно, что переходы коллоидных растворов в обыкновенные, с одной стороны, и в обычные взвеси (суспензии и эмульсии), с другой стороны — непрерывны и что отмеченные границы в известной степени произвольны; так, при величине частиц около 1 μμ в зависимости от природы вещества его раствор может в большей или меньшей степени  обладать свойствами обыкновенных растворов. Частицы в коллоидных растворах неразличимы при помощи микроскопа, они являются, по терминологии Жигмонди, «ультрамикронами»; из них частицы, размером больше 5 μ, видимые в обыкновенном ультрамикроскопе, были названы субмикронами, меньшие же частицы — амикронами. С изобретением иммерсионного ультрамикроскопа граница между суб- и амикронами отодвинута до 2 μμ.

Различие порядка размеров молекул растворителя и растворенного вещества в коллоидном растворе делает последний с оптической точки зрения гетерогенным, что особенно ярко сказывается в явлении Тиндаля. Это явление состоит в том, что путь светового луча в коллоидном растворе при рассматривании его сбоку в результате рассеяния света ультрамикронами имеет вид опалесцирующей полосы. Интенсивность света в явлении Тиндаля зависит от числа и объема частиц и от длины световой волны. В случае амикронов и субмикронов до 100 μμ, эта интенсивность, по закону Рэли (Raleigh), обратно пропорциональна четвертой степени длины волны, при больших субмикронах — третьей и даже второй степени. Этот рассеиваемый свет линейно поляризован.

Явление рассеяния света ультра-микронами позволяет сделать их видимыми, несмотря на то, что их размеры меньше разрешающей силы обычных микроскопов. В ультрамикроскопе (см. XXVIII, 617'/19'), изобретенном Зидентопфом и Жигмонди, луч света входит в коллоидный раствор сбоку, а наблюдение ведется в микроскоп, поставленный перпендикулярно к направлению луча. Этим простым методом достигается темное поле зрения в микроскопе, на фоне которого видны светящиеся точки или дифракционные кольца (см. ХХХVIІ, 558 сл.) в результате рассеяния света коллоидными частицами. В ультрамикроскопе видны не сами частицы, а свет, рассеиваемый ими. Полное сближение осветительной и наблюдательной частей прибора позволило построить иммерсионный (см. ХХVIII, 613') ультрамикроскоп, обнаруживающий присутствие частиц размером до 2 μμ. Имеются и другие типы ультрамикроскопов, как, например, ультрамикроскопы с особыми конденсаторами различных конструкций, в которых темное поле зрения достигается на принципе полного внутреннего отражения.

Цвет коллоидных растворов, весьма разнообразный, часто изменяется в зависимости от размеров частиц: так, раствор золота с частицами от 40 μμ и ниже — красного цвета, а растворы с большими частицами имеют различные цвета вплоть до синего и фиолетового. Часто густота окраски огромна: окраска раствора золота раз в 400 сильнее окраски фуксина. В общем, окраска коллоидных растворов зависит от многих факторов, в настоящее время вполне не изученных.

Различиями и размерами частиц растворенных веществ в обыкновенных и коллоидных растворах объясняется в большой степени, хотя и не вполне, явление диализа. Явление диализа было открыто Грегемом (Graham) и первое время считалось главным отличием коллоидов от кристаллоидов. Оно состоит в том, что примеси к коллоидному раствору, образующие обыкновенные растворы (и часто называемые кристаллоидами), проходят через ряд перепонок, вернее через поры в таких перепонках, между тем как ультрамикроны не могут пройти через них. Такими перепонками являются пергаментная бумага, рыбий, бычачий и др. пузыри, коллоидные мешки. Диализ играет видную роль в получении коллоидных растворов; такие растворы часто после своего получения содержат значительное количество примесей; сырой коллоидный раствор наливают в диализатор, последний помещают в чистый растворитель; указанные примеси, но не ультрамикроны, переходят через перепонку в растворитель; периодическая смена или непрерывный ток последнего позволяет удалить значительное количество указанных примесей из коллоидного раствора.

Если поры перепонки более значительны, то через них могут проходить и ультрамикроны. Обычные бумажные фильтры имеют поры шириной от 1,5 до 3,3 μ, следовательно, пропускают без изменения коллоидные растворы. Размеры пор в керамических фильтрах — от 0,16 до 0,41 μ, следовательно, тоже слишком велики, но в данном случае, как и в случае фильтров из порошкообразных веществ, проявляется их адсорбционная способность, допускающая, по крайней мере в начальный период, частичное отфильтрование растворителя. Такими фильтрами являются колбы Пукалля, свечи Чемберлена и др. Для разделения коллоидных растворов по размерам их частиц прибегают к ультрафильтрам, в которых фильтрующим материалом являются перепонки из коллодия или нитроцеллюлозы. Различные способы приготовления таких перепонок вызывают образование пор различной ширины; путем испытания их известными коллоидными растворами можно составить серии ультрафильтров для последующего разделения и характеристики неизвестных коллоидных растворов.

Ультрафильтрация дает эмпирический и часто грубый способ определения размеров частиц в данном коллоидном растворе. Более точные способы основаны на явлении диффузии (см.) их и   на скорости падения частиц под влиянием силы тяжести. По закону Стокса, в случае шарообразных частиц их радиус r = √9ηv/(D-d)g, где η – вязкость, d — плотность среды, D — плотность частиц, v — скорость их падения в данной среде, g — ускорение силы тяжести.

Оптические способы, ультрамикроскопический и основанный на явлении Тиндаля (закон Рэли), дают возможность вычислить размеры частиц в предположении их шарообразности. Однако, наиболее мощным способом является рентгенологический, позволяющий во многих случаях определить не только величину частиц, но и их внутреннее строение.

Величина ультрамикронов такова, что они должны испытывать резко выраженное броуновское движение; чем меньше частицы, тем оживленнее это движение, и по море приближения частиц к размерам обычных молекул оно переходит в молекулярное движение. Изучение броуновского движения в коллоидных растворах дало одно из самых мощных доказательств атомо-молекулярного строения вещества.

Малая величина частиц обусловливает огромную их суммарную поверхность: так, куб с ребром в 1 см имеет поверхность в 6 см²; если этот куб разделить на кубики с ребром в 0,01 μ, то их суммарная поверхность будет равна 600 м². Этот громадный рост поверхности частиц по мере уменьшения их растворов вызывает проявление энергии поверхности в коллоидных растворах, наличием каковой объясняются многие их свойства (см. адсорбция, и XII, 314/15).

Указанные выше методы позволяют вычислять размеры ультрамикронов косвенным путем, а именно в предположении их шарообразности. Изучение двойного преломления и магнитооптических явлений у ряда коллоидных растворов позволило определенно приписать таким частицам палочко- или таблицеобразную формы. Вместе с тем возникает вопрос о строении ультрамикронов, поскольку они, являясь физическими молекулами, представляют комплексы химических молекул или атомов. При образовании ультрамикрона молекулы (атомы) или частицы значительно меньшего размера могут или сливаться в одно целое с резким уменьшением суммарной поверхности, или же такие первичные частицы (α-частицы, «протоны» — по терминологии Жигмонди) не сливаются, а образуют тесный агрегат, вторичную частицу (β-частицы, «полионы»). Как те, так и другие окружаются молекулами растворителя, более тесно сближенными, чем в массе его, в случае же полиона молекулы проникают и уплотненно укладываются в промежутках между первичными частицами (ср. сольватацию, выше). Применение рентгенологического способа изучения показало в ряде случаев кристаллическую природу первичных частиц и даже позволило определить число атомов в коллоидной частице. Так, амикроны золота — кубы, а в одном из изученных растворов амикрон золота состоял из 380 атомов. Не все коллоидные частицы в основе кристалличны, есть безусловно аморфные, есть и такие, в аморфную массу которых включены ультрамикроскопические кристаллики.

Однако, представление о коллоидных частицах и растворах будет далеко не полным, если не принять во внимание их электрических свойств. Ультрамикроны, как правило, заряжены положительным или отрицательным электричеством, только в исключительных случаях они не несут зарядов. Положительно заряжены частицы в коллоидных растворах окисей железа, кадмия, алюминия и других металлов, основных красок и т. д., отрицательно заряжены частицы в растворах золота, платины, серы, сернистых соединений и т. п.

Если в коллоидный раствор погрузить электроды и пропускать ток, то в области одного электрода раствор просветлевает, в области другого делается более концентрированным; такео явление переноса коллоидных частиц к катоду или к аноду называется катафороезом. Если растворенное вещество в коллоидном растворе несет заряд одного знака, то, очевидно, растворитель должен нести заряд другого знака. Перрен построил прибор, в середине которого помещена диафрагма из порошка вещества, которое является растворенным веществом в изучаемом коллоидном растворе, по обе стороны диафрагмы впаяны электроды. Если прибор заполнить растворителем и потом пропустить ток, то растворитель передвигается через диафрагму в одну сторону, к катоду или аноду, в зависимости от знака заряда, свойственного коллоидным частицам в изучаемом случае. Такое явление носит название электроосмоса.

Скорость переноса при катафорезе ультрамикронов того же порядка, что и скорость переноса ионов (за исключением ионов водорода и гидроксила). Эти факты привели Дюкло к следующему представлению о строении коллоидных растворов. В таких растворах всегда имеются, кроме ультрамикронов, еще ионы; ультрамикрон — комплекс химических молекул растворенного вещества + сольватирующий его растворитель — может быть обозначен, например в случае раствора окиси железа, так:

такой ультрамикрон адсорбирует ион железа Fe''', обусловливающий его заряд; очевидно, в растворе должен быть противоположный ион, комбинация заряженного ультрамикрона и иона с противоположным, но эквивалентным зарядом

образует мицеллу; остальная жидкость со всеми другими растворенными веществами называется интермицеллярной жидкостью. Очевидно, что электропроводность коллоидных растворов слагается из электропроводности мицелл и интермицеллярной жидкости.

Электрическими свойствами коллоидных растворов в значительной степени обусловливается процесс коагуляции их. Если к коллоидному раствору прибавить раствор электролита, то дисперсированная фаза свертывается и выпадает в осадок. В одних случаях (коллоидные растворы главным образом неорганических веществ) выпавший осадок неспособен непосредственно переходить в раствор, в других — он после отделения от фильтрата при взбалтывании с водой вновь растворяется (например, белки). Первые называются необратимыми, вторые — обратимыми коллоидами. Процесс коагуляции проще в случае необратимых коллоидов; достаточно незначительных количеств солей, чтобы высадить в осадок коллоид; большую роль играет значность ионов прибавляемого электролита: наибольшей коагулирующей способностью обладают трехзначные ионы, например алюминия Аl'''. Так, чтобы вызвать коагуляцию раствор As₂S₃ понадобилось прибавить миллимолей на литр: хлористого натрия (NaCl) — 51,0, хлористого магния (MgCl₂) — 0,717, хлористого алюминия (АlСl₃) — 0,093. Коагулирующее действие здесь производят ионы Na', Mg'', Аl''', осаждающие их способности относятся во многих случаях как 531:7,4:1.

Ультрамикроны в растворах, с одной стороны, притягиваются, с другой, обладая одинаковыми зарядами, отталкиваются. Прибавление электролита нейтрализует их заряд, тогда проявляются силы притяжения, ультрамикроны соединяются в полионы и в конечном результате выпадают в осадок. Продукт коагуляции называется гелем. Коагуляция может быть вызвана прибавлением другого коллоидного раствора, знак заряда ультрамикронов которого противоположен заряду первого.

В случае обратимых коллоидов надо прибавить много соли, чтобы вызвать коагуляцию; здесь этот процесс сложнее. Обратимые коллоиды не только сами трудно коагулируют, но и предотвращают коагуляцию необратимых коллоидов, т. е. производят защитное действие; так, после прибавления желатины к раствору золота надо взять значительно большее количества солей, чтобы вызвать коагуляцию золота.

Свойства и строение коллоидных растворов дают ключ к пониманию и изысканию способов получения их. Только в некоторых случаях достаточно обычного приема, взбалтывания с растворителем, чтобы перевести в коллоидный раствор данное вещество (например, белок).

Разные другие способы могут быть разбиты на две группы. Конденсационные методы состоят в том, что мы исходим из обыкновенного раствора разных веществ, вызываем ту или иную химическую реакцию, в результате которой образуется вещество, неспособное давать обыкновенный раствор; эту реакцию мы ставим в такие условия, что молекулы образующегося вещества не образуют настолько больших комплексов, чтобы тотчас же выпасть в осадок, а соединяются в большие или меньшие ультрамикроны и таким образом дают коллоидный раствор Так, для получения коллоидного раствор золота можно восстанавливать щелочной раствор хлорного золота эфирным раствором фосфора или формалином; в первом случае получаются высоко дисперсированные соли красного цвета, во втором — более низко дисперсированные синего или фиолетового цветов; от других продуктов реакции мы освобождаемся диализом. Дисперсированные методы состоят в том, что большие частицы вещества разбивают на более мелкие, вплоть до ультра- или амикронов. Механический метод сводится к ударам, — понятно, в особых условиях; так, в коллоидальной мельнице данное вещество попадает под удары особых бил о воду; при вращении вала, иногда со скоростью свыше 40 м в сек, вода играет роль наковальни, а билы — молотка; в результате введенное в мельницу вещество раздробляется до ультрамикронов. Если выпавший в результате коагуляции нерастворимый гель обработать некоторыми реактивами в количествах, недостаточных для химической реакции, то гель может при последующем действии воды перейти в коллоидный раствор; такое явление носит название пептизации. Здесь дело сводится к разделению больших комплексов на ультрамикроны и к придаче последним зарядов. Электрический способ получения коллоидных растворов состоит в том, что производят вольтову дугу под водой; вещество катода переходит в коллоидальный раствор. Если исходить от вещества электрода, то такой способ является дисперсионным, но если принять во внимание, что это вещество предварительно испаряется и потом пар дает раствор, то данный метод может быть рассматриваем также как конденсационный. Учение о коллоидных растворах составляет главнейшую часть коллоидной химии, ныне выросшей в самостоятельную дисциплину. Коллоидная химия имеет не только громадное теоретическое значение в смысле освещения свойств вещества, но и не меньшее прикладное. Техника, медицина, геология за последние годы широко использовали коллоидную химию для своих целей и притом с большой пользой для себя.

Литература. W. Р. Pfeffer, «Osmotische Untersuchungen», Leipzig, 1877; J. Н. van't Hoff, «Etudes de dynamique chimique», Amsterdam, 1884 (есть русский перевод А. П. Щукарева); F. М. Raoult, «в «Compt. Rend.» 103, 1125, 1886; 104, 976, 1430, 1887; F. М. Raoult, «Cryoscopie», Paris, 1901; S. Arrhenius, «Theories of Solution», New Haven, 1912; Р. Walden, «Die Lösungstheorien in ihrer geschichtlichen Aufeinanderfolge», Stuttgart, 1910; Н. С. Jones, «The Nature of Solution», London, 1917; G. Tammann, «Ueber die Beziehungen zwischen den inneren Kräften und Eigenschaften der Lösungen», Hamburg, 1907;  Р. Duhem, «Traité élémentaire de mécanique chimique», Paris, 1899; J. J. van Laar, «Sechs Vorträge über das thermodynamische Potential», Braunschweig, 1906; van der Waals-Kohnstamm, «Lehrbuch der Thermostatik», I и II ч., 1927; G. N. Lewis and М. Randall, «Thermodynamics and the free energy of chemical substances», 1923; А. Findlay, «The phase rule and its applications», 1927; В. Курчатов, «Физико-химические теории и их приложение в технике», 1929; J. Н. Hildebrand, «Solubility», New York, 1924; Б. В. Ильин, «Молекулярные силы и их электрическая природа», М., Л., 1929; Н. А. Изгарышев, «Современная теория растворов», ГИЗ, М.; Ж. Перрен, «Атомы», ГИЗ, М. (русский перевод), 1925; R. Zsigmondy, «Lehrbuch der Kolloidchemie», 5 Aufl., 1925; В. Наумов, «Химия коллоидов», Л., 1930.

А. Раковский.