Ряд

Ряд есть выражение вида

u₀ + u₁ + u₂ +…,

где член U_n определяется местом, которое он занимает, т.  е. указателем n. Ряд называется бесконечным, если число его членов бесконечно. Если последовательность сумм s₀ = u₀, s₁ = u₀ + u₁,… s_n = u₀ + u₁ + … + u_n сходящаяся, т. е. если s_n стремится к определенному конечному пределу, когда число n неограниченно возрастает, то ряд

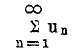
называется сходящимся, и предел sn = s – суммой ряда

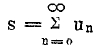
Ряды не сходящиеся называются расходящимися. Например, сходящимися рядами будут: убывающая геометрическая прогрессия  
a + aq + aq² + … (u_n = aq^n-1 s = a/(1-q)).

Ряд 1 + 1/1 + 1/1·2 + 1/1·2·3 +… (u_n = 1/1·2·…·n), s = e = 2,718… - Неперово число.

Напротив, гармонический ряд 1 + ½ + 1/3 + … (u_n = 1(n-1)) – расходящийся, причем можно доказать, что предел разности (s_n — log n) равен 0,577... (Эйлерово число), так что сумма членов гармонического ряда возрастает так же, как log n. Основная задача в теории рядов состоит в следующем: узнать, будет ли данный ряд сходящимся. Для этого пользуются признаками сходимости, которых известно очень много. Например, ряд будет сходящимся, если, начиная с некоторого n, всегда ⁿ√u_n < 1 (признак Коши), или (u_n + 1)/u_n < 1 (признак Даламбера). Ряды могут быть и кратные: например, двойной ряд

Весьма часто приходится иметь дело с рядами, члены которых суть функции одного или нескольких переменных, например,
u₀(x) + u₁(x) + … + u_n(x) + …

Исключительно важное значение таких рядов  ясно из того, что большинство функций, как в чистом анализе, так и в приложениях дается или получается именно в виде, таких рядов. Сходимость этих рядов вообще зависит от значений переменных. Ряд может быть сходящимся и представлять некоторую определенную функцию f(х), если х лежит в промежутке (а, b). т. е. если а < х < b, и расходящимся, если х лежит вне этого промежутка. Отсюда вытекает вторая основная задача в теории рядов: функция дана некоторым рядами внутри промежутка (а, b), где ряд сходится; найти свойства этой функции вне промежутка (а, b). Как пример ряда, члены которого зависят от переменных, приведем целый ряд:
a₀ + a₁x + a₂x² + … (u_n = a_nx_n), частным случаем которого является известный ряд Тейлора, дающий разложение функции в ряд при значениях а + х, близких к а,
f(а + х) = f(а) + xf’(а) + (x²/1·2)f”(a) + (x³/1·2·3)f’”(a) + …

Важный класс рядов составляют тригонометрические ряды:
А₀ + А₁ cosα₁x + B₁ sinα₂x + … = ∑^∞_n=0
A_n cosα_nx + B_n sinα_nx.

Если a_n = n, то мы получим ряд Фурье
A₀ + A₁ cos x + B₁ sin x + A₂ cos 2x + B₂ sin 2x + …

Тригонометрические ряды могут представлять функции весьма общего вида, с особыми точками; например, если дан ряд
y = sinx/1 + sin3x/3 + sin5x/5 + …, то y=0 при sinx = 0, y = +π/4 при sin x > 0, и y = -π/4 при sin x < 0.

Бесконечные ряды играют чрезвычайно важную роль в математике; в некоторых дисциплинах, например, теории дифференциальных уравнений или небесной механике, почти исключительно приходится обращаться к таким рядам. Литература громадна; много нового внесла недавно возникшая теория функций действительного переменного. См. Гурса, «Курс Анализа» (1911); некоторые из монографий Бореля («Collection de monographies sur la Théorie des fonctions, publiée sous la direction d’E. Borel») посвящены глубокому изложению теории рядов.

А. Некрасов.