Соединения в алгебре

Соединения в алгебре — группы, определенным образом составленные из данной совокупности предметов, называемых элементами. Эти элементы обыкновенно обозначаются буквами латинского алфавита. Существует три вида соединений:

1) Если в каждую группу входят все элементы данной совокупности и располагаются в ряд, по линии, то группы различаются между собой только порядком элементов и называются перемещениями (Permutation).

Число всех перемещений из m элементов обозначается через Р_m, и выражается формулой:

Р_m = 1.2.3....m.

2) Если в каждую группу входят не все элементы данной совокупности, а только определенное число их, и располагаются в ряд, по линии, то группы различаются между собой или порядком элементов, или по своему составу из элементов и называются  размещениями (Arrangement).

Число всех групп размещений из m элементов по n элементов в каждой группе обозначается через А_mⁿ и выражается формулой:

А_mⁿ = m(m-1)(m-2)…(m-n+1).

3) Если в каждую группу входят не все элементы совокупности, а только определенное число их, но порядок элементов в группе не принимается во внимание, то группы различаются между собой только своим  составом из элементов и называются сочетаниями (Combinaison).

Число сочетаний из m элементов по n элементов в каждой группе обозначается через C_mⁿ и выражается формулой:

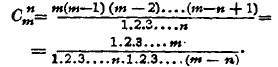
Число перемещений даже при небольшом числе элементов очень велико: например, 24 человека можно доставить в ряд следующим числом способов

620448401733239439360000.

Такие большие числа привлекали внимание древних греческих математиков: по словам Плутарха, вопросами этого рода занимался Ксенократ (397—314 г. до Рождества Христова). В Индии число размещений нашел Бхаскара (родился в 1114 г. по Рождеству Христову). В западной Европе в средние века разработка вопросов теории соединений, так называемой комбинаторики,  была выполнена заново. В XV в. Лука Пачиоли (в 1494 г.) нашел число перемещений для 10 человек; но наибольшая заслуга в этой области принадлежит французскому математику Паскалю (1623—1662 г.). Он нашел свойство числа сочетаний, выражаемое формулой:

На основании этого свойства составляется арифметический треугольник, называемый также треугольником Паскаля. Вид этого треугольника представлен на первой из приведенных ниже таблиц; а вторая таблица указывает значение отдельных чисел первой таблицы.

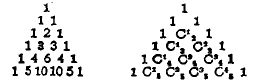
Для составления арифметического треугольника складываются два соседние числа каждой строки и сумма ставится в промежутке между двумя сложенными числами в следующей строке. Числа арифметического треугольника служат коэффициентами формулы бинома Ньютона (найденной Ньютоном в 1676 году) и называются поэтому обыкновенно биномиальными коэффициентами.

Главное применение комбинаторика имеет в теории вероятностей (см.), основание которой положено Паскалем. Развитие комбинаторики в значительной мере произошло под влиянием вопросов, выдвигавшихся теорией вероятностей.

Л. Лахтин.