Сопротивление материалов

Сопротивление материалов, или учение о прочности построек и машин, есть наука, ставящая своей задачей изучить явления, происходящие в упругих твердых телах при действии на них внешних сил, и установить на основании результатов этого изучения приемы расчета прочных размеров отдельных частей сооружений и машин. В отличие от теории упругости, которая, как чистая наука, подходит к аналогичной задаче с самой общей точки зрения и охватывает проблему работы упругих тел под действием на них внешних сил во всем ее объеме, сопротивление материалов ставит перед собой, прежде всего, практические цели и является наукой прикладной, выводы которой имеют громадное применение в технике. Изучение упругих явлений, происходящих в твёрдых телах, сопротивление материалов основывает на богатом экспериментальном материале, позволяющем установить некоторые основные рабочие гипотезы о сущности упругих явлений, и на целом ряде теоретических соображений, опирающихся на экспериментальные данные и создающих стройную теорию упругих явлений.

Ввиду чрезвычайного многообразия форм, которые принимают упругие тела в различных сооружениях и машинах, сопротивление материалов схематизирует эти формы и выделяет из них для отдельного изучения: 1) брус, т. е. тело удлиненной формы и небольших поперечных размеров, тело с длинной продольной осью; 2) пластинку, т. е. тонкое пластинчатое тело любой формы (как плоское, так и криво-поверхностное), в котором толщина незначительна сравнительно с другими размерами и 3) тело трех измерений, в котором все три измерения одного порядка. Особое внимание сопротивление материалов обращает на брус, как на тело, которое является главной  составной частью многих самых сложных сооружений и машин и которое  в то же время легче поддается детальному изучению. Пластинки и тела трех измерений изучаются частью в сопротивлении материалов, а частью в Строительной механике (см.) и в теории упругости (см. упругость). В настоящей статье мы рассмотрим лишь теорию бруса.

Изучение действия внешних сил на  брус приводит к следующим заключениям: все действующие на данный брус внешние силы, прежде всего, должны быть полностью взаимно уравновешены, т. е. удовлетворять шести уравнениям равновесия сил в пространстве, но, если выделить из бруса по длине его у какой-либо точки его оси бесконечно малый элемент ds (где s есть измерение длины оси бруса, производимое от некоей начальной точки этой оси), то справа и слева от этого элемента действующая совокупность внешних сил не обязательно уравновесится, т. е. левые силы в общем случае приводятся к силе и к паре, а правые к той же силе и той же паре, но с обратными знаками. Эти силы и пары целесообразно перенести к границам элемента ds и разложить: силы по трем направлениям: касательной (ОZ), главной нормали (ОУ) и бинормали (ОХ) к оси в точке ds, а пары по тем же трем векторам. В результате действие сил на элемент ds сводится в самом общем случае к действию:

1) двух равных и противоположных нормальных сил N_z, растягивающих или сжимающих элемент ds, смотря по знаку;

2) двух пар равных и противоположных поперечных сил Q_x и Q_y, срезывающих тело поперек его оси;

3) двух пар равных и противоположных моментов — пар М_х и М_у, изгибающих брус в двух взаимно перпендикулярных плоскостях, пересекающихся на линии, касательной к оси в точке s;

4) двух равных и противоположных моментов — пар М_z, закручивающих брус вокруг его оси.

К изучению этих четырех категорий явлений: 1) растяжении или сжатия бруса, 2) сдвига бруса, 3) изгиба бруса и 4) вручения бруса  и их различных  сочетаний и сводится задача сопротивления материалов.

Сами упругие явления, происходящие в брусе, сопротивление материалов, основываясь на результатах лабораторных исследований, подчиняет следующим законам, частью имеющим условно гипотетический характер:

1) Всякая сила вызывает изменение формы тела, причем, пока сила не перешла известного характерного для каждого отдельного упругого материала предела (предела упругости), это изменение формы пропорционально величине действующей силы (закон Гука), и по прекращении действия силы тело полностью восстанавливает свою форму.

2) Работа внешних сил, не выводящих тела за пределы упругости, измеряемая как сумма произведений всех действующих сил на перемещение точек их приложения по их направлению, полностью воспринимается упругим телом в виде упругой работы внутренних сил, развивающихся в теле одновременно с появлением в нем упругих деформаций. Эта упругая работа, или упругая энергия, обратима, т. е., она-то по прекращении действия внешних сил и восстанавливает первоначальную форму тела.

Эти два главных положения — пропорциональность изменений формы действующим силам и обратимость всего процесса, придающая всякому упругому явлению характер частного случая превращения энергии, и являются основными положениями сопротивления материалов.

Но для бруса делается еще одно существенное упрощение: условно принимается, что отдельные его поперечные плоские сечения, взятые перпендикулярно к его оси, остаются плоскими и перпендикулярными к оси, какие бы внешние силы на брус в пределах упругости ни действовали, и как бы они его оси ни искажали.

Эти общие законы и допущения справедливы только для идеально упругих тел и для идеально малых поперечных размеров бруса, ибо в телах не идеально упругих пропорциональности нет, а процесс упругого воздействия частично необратим (чисто обратимых процессов в природе по второму закону термодинамики, строго говоря, и быть не может — энергия при каждом процессе должна частично обесцениться, рассеяться). Наконец, что касается закона плоских сечений, то фактически сечения искривляются, хотя и незначительно, а потому и этот закон может быть назван лишь рабочей гипотезой.

Перейдем к изучению отдельных явлений.

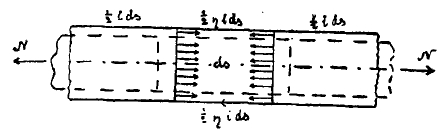
Черт. 1.

1) Растяжение — сжатие. (Черт. 1). Сила N_z, действуя центрально, вызывает встречные внутренние силы, равномерно распределенные по поперечному сечению бруса ω. Поэтому внутреннее напряжение n (средняя напряженность внутренних сил, нормальных к сечению) равно  N_z/ω. Деформация измеряется удлинением (или сокращением) длины элемента ds, отнесенным к единичной длине, т. е., относительным удлинением i=Δds/ds. Отношение n/i по закону Гука есть величина постоянная для данного материала и называется E (модуль упругости, или модуль Юнга, по имени английского ученого, впервые определившего в конце XVIII века значение Е для ряда тел). Значение величины Е для разных материалов приведено ниже. Работа упругих сил при растяжении—сжатии равна ½ N_z.i.ds,  где множитель ½  указывает на то,  что сила N_z возрастала постепенно от 0 до своего конечного значения. Ясно, что выражение

½ N_z.i.ds = ½ N_z²/Eω ds, ибо i = N_z/Eω

Выражение Eω называется жесткостью растяжения-сжатия, ибо деформация растет обратно пропорционально этой величине. При изучении растяжения-сжатия заслуживает еще внимания тот факт, что растягиваемый брус подвергается поперечному сжатию, а сжимаемый брус — поперечному расширению, что объясняется стремлением тела сохранить свой объем. Полностью это стремление не удовлетворяется, ибо поперечное сжатие в три-четыре раза менее продольного удлинения, а для сохранения объема оно должно быть ровно в 2 раза менее этого удлинения. Отношение поперечного сжатия к продольному удлинению называется коэффициентом Пуассона и обозначается буквой η.

Для характеристики каждого материала, в отношении его работы на растяжение-сжатие, следует знать: 1) те напряжения n₁  при которых упругие свойства тела прекращаются, и оно начинает изменять свою форму уже необратимым образом и затем разрушаться; 2) те напряжения n₂, при которых тело окончательно разрушается; 3) значения Е для растяжения и сжатия; 4) значение η; 5) ту полную работу, которую необходимо затратить, чтобы довести до предела упругости тело из данного материала при объеме его, равном единице. Последняя величина называется «живым упругим сопротивлением» и легко определяется из предыдущих формул, как n²/2E.

Величины n₁, n₂, Е даны в конце статьи в особой таблице при описании приемов экспериментального исследования упругих явлений.

2) Сдвиг. Силы Q вызывают внутренние силы, расположенные не нормально к сечению, а в плоскости самого сечения, и распределенные по сечению неравномерно (черт. 2). Их среднее значение назовем через t (тангенциальное, т.   е., касательное к сечению напряжение).

Черт. 2.

Очевидно, что t = Q/ω. Мерой деформации здесь будет отклонение конечной точки элемента ds вбок (т. е., перпендикулярно к длине элемента), отнесенное к самой длине ds, т. е., относительный сдвиг Θ =  Δ’ds/ds. По закону Гука и здесь имеется свой модуль

G = t/Θ, откуда Θ = Q/Gω. Некоторые теоретические соображения устанавливают, что G (в зависимости от значения величины η) равно от 0,375 Е до 0,400 Е, т. е., есть функция от Е и η. Опыты достаточно хорошо подтверждают эти соотношения для однородных тел.

Работа сдвига равна ½ Q²/Gω ds и Gω называется жесткостью сдвига.

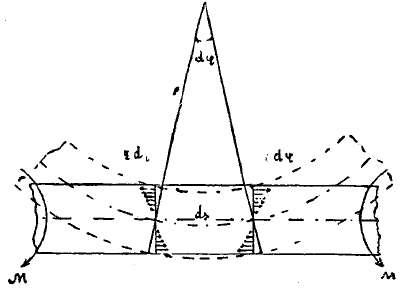
Черт. 3.

3) Изгиб. При изгибе бруса его поперечные сечения поворачиваются вокруг оси, совпадающей с вектором изгибающей пары М и проведенной через центр тяжести сечения (черт. 3). Ясно, что при этом отдельные продольные волокна бруса частью растягиваются, а частью сжимаются и притом тем больше, чем дальше данное волокно отстоит от оси поворота, т. е., от центра тяжести сечения. В результате получается сочетание растяжения с сжатием, причем основные предельные упругие напряжения и модули остаются те же. Мерой деформации здесь является кривизна, характеризующая то искривление прямого первоначально бруса, которое получается в результате поворота отдельных сечений. Эта кривизна, выражаемая, как известно, величиной, обратной радиусу искривления ρ, определяется формулой: 1/ρ = М/EI, где М и Е имеют известные нам значения, а I есть особый геометрический фактор, характеризующий сопротивление площадки поворачиванию ее вокруг оси, совпадающей с направлением вектора изгибающей пары. I называется моментом инерции сечения, выражается формулой I_х = ∫y².dω и играет большую роль в сопротивлении материалов. Величина ЕI называется жесткостью изгиба.

Черт. 4.

Напряжение при изгибе развивается нормальное — n — и растет по линейному закону в обе стороны от оси бруса. На единичном  расстоянии от оси оно равно (n₁) = M/I, т. е. также зависит от величины I, но уже не зависит от величины Е. Работа при изгибе равна ½ M²/EI ds. Упругие постоянные остаются те же, как и для растяжения-сжатия.

4. Кручение. При кручении круглого бруса его продольные волокна закручиваются по винтовой линии, и мерой деформации является угол закручивания на единицу длины (черт. 4). Он определяется из формулы α = M_z/GI_z, где I_z есть также момент инерции сечения, но уже относительно оси QZ, и характеризует сопротивление сечения поворачиванию вокруг этой оси, перпендикулярной к площади сечения. Напряжения развиваются тангенциальные, растут от центра к окружности, и (t₁), т. е., тангенциальное напряжение на единичном расстоянии от центра, определяется так:

(t₁) = M_z/I_z – формула, аналогичная формуле изгиба. Работа выражается, аналогично предыдущему, как ½ M_z²/I_z ds. Величина GI_z есть жесткость кручения. Если свести все предыдущие данные в одну схему, то получим следующую таблицу:

Таблица работы элемента ds

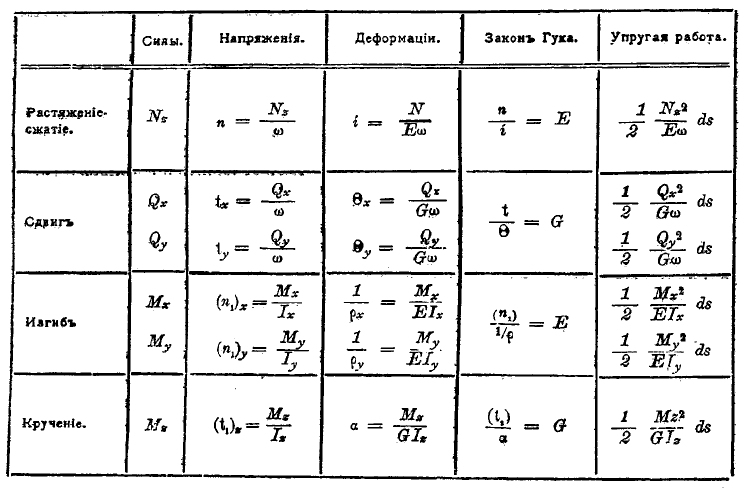
Очевидно, что работа бруса получается интегрированием элементарных работ по всей длине оси бруса.

В отдельных частных случаях (для бруса очень большой кривизны или, при кручении, для бруса не круглого сечения) выражение работы несколько усложняется, но основные черты его остаются те же — это всегда есть однородная функция второй степени от величин N_z, Q_x, Q_y, М_z, М_x, М_y.

Современная теория сопротивления материалов все свои выводы основывает на изучении выражения работы. Распространяя принцип Лагранжа (работа сил по возможным для данной системы перемещениям равна нулю) на упругие системы, сопротивление материалов приходит к важному выводу, что производная от работы по какой-либо силе равна перемещению точки приложения этой силы, а производная от той же работы по какому-либо перемещению равна силе, приложенной по направлению этого перемещения (теорема Кастильяно).

Эта основная теорема связывает в самой общей форме силы и перемещения (причины и следствия явления) и, в частности, давая перемещения в линейной зависимости от сил, формулирует в самом общем виде закон Гука (линейная зависимость получается потому, что выражение работы есть функция второй степени, а, следовательно, его производная есть функция линейная).

Общая связь между причинами, вызывающими упругие явления в брусе, и следствиями, вызываемыми этими причинами, находит себе особо ясное выражение в так называемой схеме шести строк.

Если назвать первой строкой математические выражения, определяющие закон изменения нагрузок по длине бруса, второй строкой — закон изменения по той же длине величин N_z, Q_x, Q_y, а третьей — закон изменения величин М_z, М_x, M_у, то легко доказать, что вторая строка получается интегрированием первой, а третья — интегрированием второй, и, обратно, высшие строки могут быть получены, как производные от низших.

Эта связь имеет большое значение в теории сопротивления материалов и, в частности, указывает и на зависимость между внутренними силами, ибо вышеприведенная таблица ввязывает их значение со значениями величин N_z, Q_x, Q_y, М_z, М_x, М_у. Можно установить, что внутренние силы вызываются частью непосредственно нагрузкой — первая строка (так называемые местные напряжения (n) и (t)), частью величинами N_z, Q_x, Q_y, — вторая строка (напряжения n и t по нашей таблице) и частью и более всего величинами М_z, М_x, М_у, — третья строка (напряжения изгиба и кручения — (n₁) и (t₁)). Остальные три строки характеризуют уже деформации и перемещения, а именно: четвертая строка — искривления малого элемента ds, пятая — углы отклонения касательной к оси в данной точке от ее первоначального направления (девиации), а шестая — конечные перемещения отдельных точек оси. Интегральная связь между этими тремя строками ясна, ибо если четвертая строка характеризует кривизну, то пятая (угловое перемещение) есть ее интеграл, а шестая — линейное перемещение — должна быть интегралом пятой.

Выше охарактеризованное общее выражение упругой работы связывает, наконец, третью строку с четвертой, ибо нам известно, что кривизны изгиба и углы закручивания (т. е. кривизны кручения) связаны с величинами М_z, М_x, М_у простой линейной зависимостью. В результате получается та связь всех шести строк, которая, например, для простейшего случая действия всех сил параллельно друг другу и перпендикулярно прямой оси бруса выражается дифференциальным уравнением:

EI_x d⁴y/dz⁴ = - p_y

где EI_x – есть  жесткость изгиба относительно оси ОХ, перпендикулярной плоскости действия сил; у и z — текущие координаты изогнутой оси, из которых у — опускание оси бруса параллельно действующим силам (ирогиб), а z — расстояние данной точки оси бруса от ее начала; р_у — нагрузка, параллельная оси ОУ и приходящаяся на единицу длины бруса в данном месте.

Это-то уравнение и другие, ему аналогичные для более сложных случаев действия сил, и связывают причину со следствием, нагрузку с прогибом и вообще действующие силы с перемещениями отдельных точек.

Сопротивление материалов более всего интересуется вопросами изгиба (и лишь в частности, в применении к машиностроению — вопросами кручения), и выше приведенные общие соображения широко применяет к расчету балок, т. е., тех именно брусьев с прямой осью и с перпендикулярной к этой оси нагрузкой, расчетное дифференциальное уравнение которых дано выше.

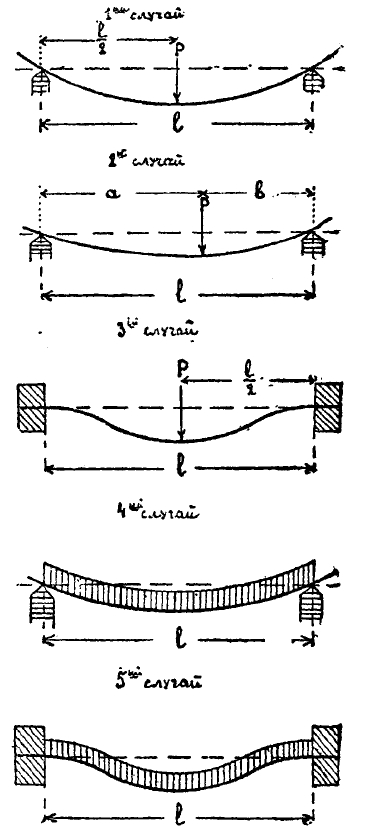
Черт. 5.

Особое значение имеют следующие случаи (черт. 5):

1. Если балка свободно лежит на двух опорах, имеет длину между опорами (пролет) 1 и нагружена одним грузом Р посредине, то максимум M = Pl/4 (посредине пролета) и максимум y = 1/48 Pl³/EI (также посредине пролета).

2. Если та же балка нагружена тем же грузом, отстоящим от левой опоры на величину а, а от правой на величину b, то maximum М = Pab/I (под грузом), а прогиб под грузом y = Pa²b²/3EII.

3. Если та же балка обоими своими концами заделана в стену, то при одном грузе посредине maximum

М = Pl/8 (под грузом), а maximum

y = 1/192 Pl³/EI (тоже под грузом).

4. Если та же балка не заделана концами и нагружена сплошной нагрузкой интенсивности р, то maximum

М = Pl²/8 (посредине), а maximum y = 1/384 Pl⁴/EI (посредине).

5. Если при той же нагрузке та же балка заделана, то maximum М = Pl²/24  (посредине) и в то же время minimum M = - pI²/12 (на опорах) и максимум y = 1/384 pI⁴/EI (посредине).

Таким образом, заделка концов уменьшает момент под грузом от 2 до 3 раз, а прогиб посредине – от 4 до 5 раз.

Широкое применение имеют неразрезные балки, т. е. прямые брусья, покоящиеся на многих опорах, — при этих условиях каждый пролет оказывается как бы частично заделанным, благодаря присутствию соседних пролетов.

В пределе, при бесконечном числе пролетов, каждый становится (при сплошной загрузке всей балки) как бы совершенно заделанным. Вообще как моменты, так и прогибы в неразрезных балках значительно меньше таковых же в балках того же пролета, свободно лежащих на опорах.

Из других категорий брусьев, подробно изучаемых в сопротивлении материалов, заслуживает упоминания арка — кривой брус, выгнутый осью вверх и воспринимающий внешнюю нагрузку. Если эта арка заделана своими концами в опоры, то на этих концах развиваются особые моменты заделки, удерживающие арку в заделанном положении. Кроме того, на этих же опорах развивается и горизонтальная сила—распор, препятствующая раздвижению концов арки.

Если рассматривать арку, пролетом в 1 единиц и подъемом в 1 единиц (f — стрела подъема), нагруженную сплошной нагрузкой р весовых единиц на каждую единицу длины проекции арки (черт. 6.), то мы получим для параболического очертания оси арки и при постоянном сечении:

1) При нагрузке, занимающей весь пролет: распор Н = pI²/8f и М по всему пролету равно нулю (т. е., отдельные элементы такой арки лишь сжимаются силой N_z — изгибающих моментов нет).

2) При нагрузке, занимающей всю левую половину пролета:

распор Н = pI²/16f; момент в левой опоре М_А = - pI²/64; наибольший момент около 3/16 l, а именно максимум М_{3/16 l} = + 9/1024 pI².

Более подробное исследование отдельных сооружений входит уже в область Строительной механики (см.), хотя трудно провести резкую грань между этими двумя техническими науками и ныне существует стремление слить их в одну общую науку: «Теория инженерных сооружений».

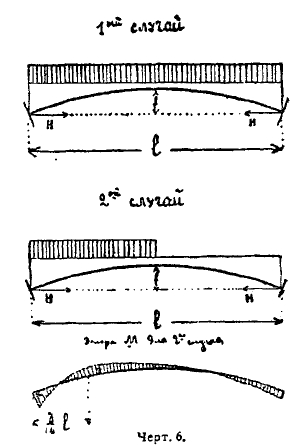
Черт. 6.

Все вышеизложенное представляет собой расчет бруса на прочность и жесткость, причем прочность характеризуется достаточно малым значением внутренних сил, т. е., напряжений n и t, которые должны быть значительно менее пределов упругости (см. ниже таблицу), а жесткость — достаточно малыми деформациями отдельных элементов и перемещениями отдельных точек оси бруса. Но наряду с этим необходимо проверить брус на устойчивость приданной ему формы деформации. Если мы сжимаем длинный брус, то у нас не может быть уверенности, что он в сжатом состоянии останется прямым и не начнет выпучиваться: если мы изгибаем вертикальными силами высокий плоский брус, лежащий на двух опорах (например, поставленную на ребро линейку), то мы не можем быть уверены, что брус останется в плоскости действия  сил и не начнет крутиться и «ложиться» в средней своей части, даже если концам его обеспечено сохранение вертикальности ребра; если мы крутим тонкую круглую проволоку, мы не можем быть уверены, что ось ее останется прямой и не начнет сама закручиваться в спираль. Эксперименты и теоретические соображения согласно указывают, что все вышеотмеченные явления неизбежно произойдут, если действующие силы и пары перейдут известный предел, часто значительно низший того, при котором внутренние силы при первичном явлении (т. е., в наших примерах при сжатии, при простом изгибе и при простом кручении) станут мало-мальски значительными. Так, деревянный брусок сечением в один квадратный сантиметр имеет предел упругости на  сжатие приблизительно в 150 кг/см², т. е., нагрузка 150 килограммов для него   еще не опасна. Однако, если он имеет длину в 100 сантиметров, то   нагрузка в 8 килограммов, дающая внутреннее напряжение при первичном явлении всего в 8 кг/см², уже вызывает катастрофическое выпучивание (черт. 7).

Черт. 7.

Сила, или момент, вызывающие уже начало вторичных явлений (т. е., в наших примерах выпучивание, кручение и поворот сечения, спиралевидное закручивание оси), называются критическими.

Теоретические исследования указывают, что эти критические величины пропорциональны наименьшей жесткости тела в отношении его сопротивления вторичным явлениям и обратно пропорциональны квадрату длины тела (при критической силе) и первой степени его длины (при критическом моменте).

Для разобранных случаев мы имеем:  

а) при простом сжатии длинного стержня (продольный изгиб)

P_{критич.} = π² min.EI/I²

(Эйлер).

б) при изгибе поставленной на ребро линейки

P_{критич.} = 16,94 √GI_e.min.EI/I²

(Тимошенко).

в) при кручений тонкого длинного круглого тела

М_{критич.} = π GI_z/I

(Гринхил).

Знание этих величин в отдельных случаях позволяет нам проверять элементы сооружений и машин на устойчивость.

Наконец, за последнее время большое внимание обращается на динамическое действие нагрузки, т. е., на действие силы, приложенной с ускорением по ее направлению. При этом как деформации, так и внутренние напряжения значительно (во много раз) превосходят статическое значение тех же величин. В некоторых случаях, когда прилагаемые извне периодически действующие динамические силы длительного характера вызывают так называемые «вынужденные колебания» системы, имеется  еще и опасность так называемого «резонанса», т. е., совпадения периода  «вынужденных» колебаний с периодом «собственных» колебаний системы. (Последние могут быть определены путем отведения системы от и состояния ее равновесия и устранения затем отводившей силы. Тогда тело подвергается «собственным» колебаниям). Если периоды вынужденных и собственных колебаний совпадают, то теоретически амплитуды колебаний доходят до бесконечно больших размеров, и тело должно разрушиться. Неполная упругость тела и сопротивление среды смягчают это явление, но не устраняют вовсе грозящих сооружению от резонанса опасностей.

Совокупное изучение всех вышеизложенных факторов в целях обеспечения для каждой данной детали сооружения или машины длительной безопасной работы и называется расчетом сооружения.

Литература: на русском языке: В. Л. Кирпичев, «Сопротивление материалов»; Н. Н. Митинский, «Строительная механика»; С. П. Тимошенко, «Курс сопротивления материалов»; П. А. Велихов, «Теория инженерных сооружений». На иностранных языках: С. Bach, «Elastizität und Festigkeit»; А. Föppl, «Vorlesungen über technische Mechanik»; I. Ewing, «The strength of Materials»; H. Résal, «Resistance des matériaux». А.und L. Föppl, «Drang und Zwang».

Экспериментальные исследования по сопротивлению материалов. Все вышеизложенные теории базируются, прежде всего, на экспериментальном материале, получаемом путем опытных определений упругих свойств отдельных тел, применяемых в технике. Впервые опыты над упругими телами были поставлены Галилеем в 1638 году в венецианском арсенале. Позднее ряд экспериментаторов занимался теми же вопросами, но лишь со второй половины XIX века появились в главнейших научных центрах мира специальные механические лаборатории, имеющие своей задачей систематическое изучение упругих свойств материалов, применяемых в технике. В настоящее время можно назвать ряд крупных лабораторий, выдвинувшихся своими работами и своим оборудованием на первое место среди других: Берлинская Государотвенная Испытательная Станция в местечке Gross-Lichterfelde West под Берлином; Национальная Лаборатория в Teddington’е близ Лондона; Палата Стандартов в Вашингтоне (Америка). В России наибольшей известностью пользуются: Лаборатория Петроградского Института Инженеров Путей Сообщения (старейшая, основана в 1853 году профессором Собко, с 1873 года до 1922 года (49 лет) возглавлялась профессором Н. А.  Белелюбским (умер в 1922 году)  и Государственный Научно-Технический Институт в Петрограде. В Москве крупнейшими являются Лаборатории Московского Высшего Технического Училища (профессор И. А. Калинников) и Московского Института Инженеров Путей Сообщения (профессор Л. Д. Проскуряков и профессор П. А. Велихов).

Задачи механических лабораторий следующие:

1) установить основные положения теории сопротивления материалов;

2) определить упругие постоянные для отдельных тел, применяемых в технике;

3) проверять экспериментально новые теории в области сопротивления материалов и устанавливать степень их применимости к отдельным материалам.

Методы, которыми пользуются механические лаборатории, заключаются в применении мощных и в то же время точных машин, позволяющих осуществить в лабораторной обстановке отдельные явления, изучаемые сопротивлениями материалов, в их чистом виде: растяжение-сжатие, сдвиг, изгиб, кручение — с возможно полным устранением побочных факторов, и измерить возможно точно, как причинные факторы — действующие силы и моменты, так и вызываемые ими следствия — деформации и перемещения.

Наибольшее значение имеют опыты на растяжение и сжатие.

Машины, применяемые при этих опытах, дают в последнее время исключительную мощность: до 4500 тонн на сжатие (машина Ольсена в Питтсбурге) и до 500 тонн на растяжение (машина Эмери в Палате Стандартов в Вашингтоне). В то же время точность измерений доводится до того, что та же машина Эмери регистрирует каждый килограмм возрастающей нагрузки, а в некоторых машинах можно читать и доли грамма; при измерении деформаций применяются приборы, отмечающие десятитысячные доли миллиметра.

Производство испытаний на растяжение и сжатие. Образец на растяжение должен иметь длинную призматическую форму и быть центрально закреплен в машине. Нагрузка на образец должна возрастать медленно—статически. Наиболее употребительные машины суть или рычажные, или гидравлические, и в обоих случаях достижимо медленное возрастание нагрузки. Схема современной испытательной машины: (Мера и Федергафа) показана на чертеже 8-м. При измерении упругих деформаций необходимо снимать размеры с самого испытуемого образца. В то же время снимается и автоматическая диаграмма, регистрирующая отношение между напряжением и деформацией. Когда это отношение потеряет свою линейную форму, тогда закон Гука может считаться нарушенным и упругие свойства потерянными — это и есть предел упругости или, что почти то же, предел пропорциональности. Взяв для него отношение n/i, находим Е. Дальнейший ход процесса сопровождается быстрым ростом деформаций при медленном росте напряжений и заканчивается разрушением — разрывом образца. При этом определяется предельное напряжение, выдержанно образцом (разрушающее или «временное» сопротивление), и то удлинение, которое получил образец за пределами упругости, и которое уже неупруго — остаточное удлинение. Оно определяется в долях от некоторой условной расчетной длины и характеризует степень пластичности материала, способность его к обработке.

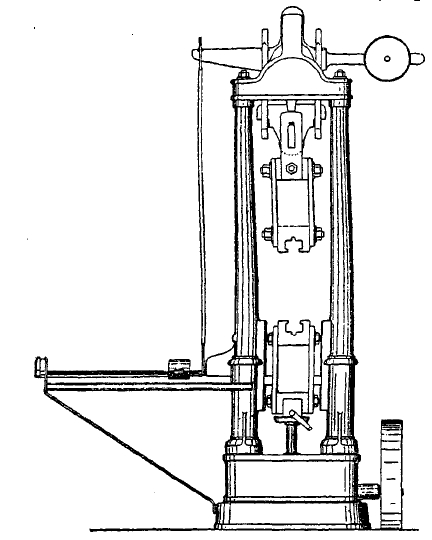
Черт. 8. Машина Мора и Федергафа на 50 тонн.

Опыты на сжатие производятся тем же порядком, только образцу придается форма правильного куба или цилиндра. Все явления протекают так же, и в результате получаются те же характерные цифры. Кроме этих двух классических видов испытаний, нередко производятся и испытания на изгиб и кручение, причем последние позволяют определить модуль G по формуле

(определение G при опытах на сдвиг встречает некоторые затруднения).

В последнее время большое внимание уделяется опытам с динамическим действием нагрузки и так называемым испытаниям на «усталость» металла. Сущность явления «усталости» заключается в том, что ни одно нагружение не проходит для материала бесследно, — ввиду отсутствия идеально-упругих тел в природе материал при всякой нагрузке немного как бы «надрывается» — частично деформируется неупруго; этот «надрыв» особенно силен близ  предела упругости и в результате приводит к разрушению материала, многократно нагружаемый нагрузкой, близкой к пределу упругости, и даже несколько меньшей этого предела. Опыты на  усталость указывают, в какой степени возможно безопасно приближаться к пределу упругости при выборе допускаемых рабочих напряжений.

Это обстоятельство имеет особое значение в связи с тем, что многие сооружения и машинные части в течение периода своей работы подвергаются миллионам и сотням миллионов повторных рабочих нагрузок: мост должен пропустить до 2 миллионов поездов, паровозная ось должна совершить до 400 миллионов оборотов, т. е., ее волокна 400 миллионов раз должны переходить от максимального растяжения к максимальному сжатию, а ось паровой турбины совершает за время своей службы до 15 миллиардов  оборотов.

Результаты экспериментальных исследований и допускаемые рабочие напряжения приведены для главнейших материалов в следующей таблице (все величины в килограммах на квадратный сантиметр):

Материал			Предельное допускаемое рабочее напряжение	Предел упругости или пропорциональности	Модуль Е	Временное или разрушающее напряжение
Железо мостовое	растяжение		1400	2200	2150000	4000
	сжатие
Сталь рельсовая	растяжение		1800	3500	2200000	6000
	сжатие
Чугун литейный	растяжение		250	1800	800000	2000
	сжатие		750	6000	1000000	8000
Сосна		растяжение	120	300	90000	800
		сжатие	80	150	100000	400
Дуб		растяжение	160	450	110000	1000
		сжатие	90	150	105000	500
Песчаник твердый		растяжение	-	-	120000	30
		сжатие	30	-	150000	800
Гранит		растяжение	-	-	240000	40
		сжатие	60	-	300000	1500
Портланд цемент чистый		растяжение	10	-	180000	70
		сжатие	70	-	250000	700
Бетон плотный		растяжение	5	-	85000	30
		сжатие	40	-	140000	300

 

В таблице даны средние круглые цифры, которые сильно колеблются для отдельных случаев. Также и допускаемые напряжения различны в разных государствах, — в таблице даны обычные русские нормы последних лет.

Литература: А. Martens, «Materialienkunde»; О. Wawrziniok, «Handbuch des Materialprüfungswesens»; Р. Breuil. «Nouveaux mécanismes et nouvelles méthodes pour l’essai des métaux». На русском языке см. Н. Н. Митинский, «Строительная механика» (описание приборов и методов испытания и таблица упругих постоянных).

П. Велихов.