Спектральный анализ

Спектральный анализ. В следующих статьях находятся те сведения, на которые мы будем ссылаться и содержание которых будем считать известным: дисперсия (XVIII, 402), излучение (XXI, 474), колебательное движение (XXIV, 482), свет (XXXVII, 530). Напомним бегло наиболее существенное. Световые лучи, испускаемые различными телами, всегда представляют смесь различных лучей, которые можно отделить друг от друга при помощи призмы из стекла, кварца или иного подходящего вещества, или посредством дифракционной решетки (см. свет). При этом лучи располагаются рядом, давая полосу, которая называется спектром. Если за источник световых лучей взять добела раскаленное тело или яркое пламя, то спектр представляется в виде непрерывной полосы, которую принято разделять на семь частей: красную, оранжевую, желтую, зеленую, голубую, синюю и фиолетовую. В действительности цвета постепенно переходят один в другой, так что указанное деление более или менее произвольно. Для удобства условимся считать, что спектр расположен горизонтально, и что красный конец находится слева, а фиолетовый справа. Концы спектра не резки; цвета делаются все темнее, и, наконец, впечатление окраски черного фона исчезает. Положение концов непрерывного спектра зависит от чувствительности глаза и неодинаково для различных людей. Свет есть распространяющееся колебательное движение. До восьмидесятых годов истекшего столетия господствовало учение, считавшее, что это суть упругие колебания, распространяющиеся в эфире. Это учение ныне вполне оставлено и заменено электромагнитной теорией света (см. свет), согласно которой свет есть распространяющееся электромагнитное колебание (возмущение). Скорость света, т. е. расстояние, которое световые лучи проходят в одну секунду, обозначим через v; скорость света в пустоте через с. Последняя не зависит от рода луча и равна 3·10¹⁰см, т. е. 300 000 км/сек. Вообще же скорость v зависит от той среды, в которой лучи распространяются, и от рода луча. Время одного колебания называется периодом; обозначим его через Т. Число колебаний, совершаемых в 1 секунду, обозначим через ν; очевидно ν=1/Т. Длиной волны λ называется то расстояние, на которое свет распространяется в течение времени Т. Чем быстрее происходят колебания, т. е., чем меньше Т и чем больше ν, тем меньше длина волны λ. Величины v, T, ν, λ связаны основными уравнениями:

λ = vТ, v = νλ; λ = сТ, с = vλ ... (1)

Последние два равенства относятся к пустоте. Число n волн, укладывающихся на длине одного сантиметра, называется волновым числом; очевидно n = v/с;

n = 1/λ (см) = 10⁸/λ (Å) … (2)

где λ должно быть выражено в сантиметрах или в ангстремах (см. ниже). Число v еще называется частотой колебаний. Лучи, соответствующие различным частям спектра, отличаются друг от друга величинами n, v, Т и λ, причем слева направо растут n и v, убывают Т и λ, так что красные лучи имеют наибольшую, фиолетовые — наименьшую длину волны λ. Свет представляет частный случай несравненно более общего явления, называемого лучистой энергией, все виды которой, по существу, отличаются друг от друга только частотой колебаний ν (или волновым числом n) или длиной волны λ. Спектр видимый (световой) составляет весьма малую часть всего спектра лучистой энергии, который делят на следующие пять частей, из которых четыре обширнейшие невидимы, т. е. нашим глазом не воспринимаются: I. Лучи видимые. II. Лучи инфракрасные, спектр которых тянется слева от красного конца видимого спектра. III. Лучи Терца или лучи электрические, которыми пользуются при беспроволочной телеграфии и телефонии. Их спектр расположен еще более налево, т. е. за спектром лучей инфракрасных. IV. Лучи ультрафиолетовые, спектр которых тянется справа от фиолетового конца видимого спектра. V. Лучи Рентгена, спектр которых расположен далеко справа от спектра лучей ультрафиолетовых. Если идти слева направо, т. е. в порядке возрастающих частот колебаний v (и волновых чисел n), или убывающих длин волн λ, то части спектра лучистой энергии оказываются в следующем порядке: лучи Герца, инфракрасные, видимые, ультрафиолетовые и лучи Рентгена. Весь спектр лучистой энергии можно разделить на октавы, взяв этот термин из учения о звуке. Октавой называется расстояние друг от друга, точнее — интервал двух лучей спектра, из которых длина волны одного в два раза меньше длины волны другого, или частота в два раза больше. Длины волн принято выражать в различных единицах длины, смотря по положению луча в спектре. Для лучей Герца длины волн выражают в километрах, метрах, сантиметрах и миллиметрах. В инфракрасной части пользуются исключительно единицей длины μ, которая равна 0,001 мм. Длины волн в видимой части выражают иногда в единицах μ; редко в μμ (10^—6 мм) и чаще всего в ангстремах Å (шведская буква, которая выговаривается, как русское О), причем Å = 0,1μμ = 10^-4 μ = ^10-7 мм = 10^—8 см. Длины волн ультрафиолетовой части спектра выражаются исключительно только в ангстремах. Наконец, длины волн лучей Рентгена выражаются в ангстремах или в недавно введенных иксах Х, причем

Х = 0,001 Å = 10⁷μ = 10^-10 мм = 10^-11 см.

Предела спектра с левой стороны не существует, так как можно получить лучи Герца произвольной длины волны. Однако, лучи, длина волн которых превышает несколько километров, не представляют ни чисто научного, ни технического интереса. Поэтому мы ограничим спектр слева лучами, длина волны которых равна 4 километрам; такими лучами пользуются в телеграфии без проводов. С правой стороны спектр рентгеновых лучей доходит до λ = 0,1Å = 100 Х. Однако, отчасти еще дальше расположен спектр лучей γ, испускаемых радиоактивными веществами. Эти лучи вообще по своим свойствам тождественны с лучами Рентгена, и спектры тех и других отчасти сливаются. Но уже были измерены такие длины волн лучей γ, которые оказались равными 0,07 Å = 70 Х. Нет сомнения, что спектр лучей у тянется еще дальше вправо, но длины волн этих ультра-рентгеновых лучей еще не были измерены. В нижеследующей табличке указаны для всех частей спектра лучистой энергии: предельные длины волн λ (слева и справа), предельные частоты v и размеры этих частей, выраженные в октавах.

Лучи	Длины волн λ		Частоты ν		Размер октавы
	Слева	Справа	Слева	Справа
Герца	4 км	2 мм	75000	1,5·1012	20 ½
Инфракрасные	340 μ (0,34 мм)	0,76 μ	9·1011	4·1012	9
Видимые	0,76 μ	0,4 μ (4000 Å)	4·1014	7,5·1012	Менее одной
Ультрафиолетовые	4000 Å	136 Å	7,5·1014	2,2·1016	5
Рентгена и γ	17,66 Å	0,07 Å (70 Х)	3·1017	3·1019	7

Остаются две не окончательно исследованные области: I. Между лучами Герца и инфракрасными; длины волн от 2 мм  до 0,34 мм, всего около 2 ½  октав. II. Между ультрафиолетовыми и рентгеновыми лучами; длины волн от 136Å до 17,66 Å, всего менее 3 октав. Вся длина спектра лучистой энергии, произвольно считаемого от λ = 4 км, равна, примерно, 48 октавам, из которых менее одной приходится на спектр лучей видимых. Исследованная инфракрасная часть почти в 10 раз длиннее видимой. Длина волны крайнего справа луча (70 Х) в 4·10¹⁴ (400 миллион миллионов) раз меньше избранного нами крайнего луча слева (4 км) и во столько же раз частота первого больше частоты второго. Для дальнейшего нам необходимо напомнить те условия, при которых возникают лучи Рентгена (с лучами Герца мы вообще встречаться не будем). Главнейший их источник — так называемая рентгенова «трубка» — это закрытый со всех сторон, приблизительно шаровидный сосуд, обычно из стекла. В нем находятся три металлические пластинки: катод, анод и антикатод; воздух из него выкачан до высокой степени разрежения. Через трубку пропускается электрический ток, причем из катодной пластинки вылетает, перпендикулярно к ее поверхности, поток электронов, т. е. мельчайших частиц отрицательного электричества, составляющих так называемые катодные лучи. Скорость электронов при выходе их из катода весьма незначительна. Но между катодом и антикатодом устанавливается разность потенциалов (электрическое поле), вследствие чего электроны ускоряются и ударяют в поверхность антикатода, обладая огромной скоростью. В том месте, где электроны встречают поверхность антикатода, возникают рентгеновы лучи. Мы увидим, что их характер зависит от того вещества, которым покрыта поверхность антикатода.

Когда рентгеновы лучи падают на поверхность какого-либо тела, то эта поверхность с своей стороны начинает испускать такие же лучи; они называются вторичными рентгеновыми лучами. Рассмотрим различные виды спектров. Прежде всего, отличают спектры испускания и спектры поглощения. Первые определяют собой состав лучистой энергии, испускаемой данным источником этой энергии. Они зависят исключительно только от рода источника и от его состояния, т. о., например, от температуры, давления и других физических условий. Отличают три вида спектров испускания, а именно: I. Спектры сплошные, которые получаются, главным образом, от накаленных твердых и жидких тел, но также и от других источников (см. ниже). Белые лучи, испускаемые твердыми и жидкими накаленными телами, дают сплошной спектр, конец которого с правой стороны зависит от их температуры. Тела не очень горячие, т. е. не испускающие видимых лучей, дают спектр, который весь расположен в инфракрасной части. При повышении температуры интенсивность этого спектра увеличивается, и в то же время спектр удлиняется направо, т. е. в сторону лучей видимых. При некоторой температуре появляются лучи красные, затем оранжевые, желтые и т. д. до фиолетовых и ультрафиолетовых, когда тела накалены добела. II. Спектры линейные, представляющие наибольший интерес, так что к ним относится почти вся наука о спектрах. Эти спектры состоят из отдельных линий, расположенных вертикально, когда весь спектр тянется, как мы предположили, горизонтально. Длина этих линий, равная ширине спектра, зависит от длины той вертикально расположенной щели, через которую исследуемый поток лучистой энергии вступает в прибор, служащий для его разложения в спектр (см. ниже). Если спектральные линии находятся в видимой части спектра, то их окраска зависит от их длины волны, т. е. от того места, которое они занимают в спектральной полосе. Линейные спектры получаются при разложении лучистой энергии, испускаемой при определенных условиях (см. ниже) газами и парами, свечение которых может быть вызвано введением их в слабо светящееся пламя, например спирта, пропусканием через них электрического тока (гейсслеровы трубки), вольтовой дугой (XI, 192) или электрической искрой. Число и распределение спектральных линий по всем частям спектра зависит от рода и состояния вещества. От этого же зависит и относительная яркость, точнее говоря — интенсивность отдельных линий. Рентгеновы лучи также могут дать линейный спектр. III. Спектры полосатые, состоящие из ряда полос различной ширины, которые при достаточно сильной дисперсии оказываются состоящими из огромного числа отдельных, весьма близких друг к другу линий. Они получаются от светящихся газов и паров. В настоящее время вполне установлено, что линейные спектры испускаются атомами, т. е. одноатомными газами и парами, каковы гелий, благородные газы и пары металлов, или двуатомными, молекулы которых подверглись диссоциации (XVIII, 411), т. е. распаду на отдельные атомы; полосатые же спектры испускаются молекулами, т. е. дву- или многоатомными газами и парами, не подвергшимися диссоциации. В весьма многих случаях газы и пары  дают смешанные спектры, в которых рядом с линиями встречаются также и отрезки сплошного спектра, которые не могут быть приняты за полосы полосатого спектра, так как они ни при какой дисперсии не разлагаются на отдельные линии. Так, спектр рентгеновых лучей всегда содержит сплошную часть, на фоне которой при известных условиях (см. ниже) выступает спектр линейный. Такие сплошные части иногда называются «белыми», по аналогии со сплошным спектром, который дают белые видимые лучи. Говорят, например, о белом рентгеновском спектре, хотя рентгеновы лучи невидимы. Спектры поглощения получаются, если лучи источника, дающего сплошной спектр, пропустить через слой какого-либо испытуемого вещества, которое поглощает, т. е. не пропускает через себя, те или другие лучи. Лучи, прошедшие через этот слой, дают затем спектр, представляющий как бы обратное от спектра испускание. Он состоит из сплошного спектра, на фоне которого находятся темные (при полном поглощении — черные) линии, полосы, распадающиеся на множество отдельных линий, или сплошные темные части. Спектр поглощения зависит исключительно только от того вещества, через слой которого прошли белые лучи, от толщины этого слоя и от состояния вещества, например от его температуры, давления и т. д. Связь между спектрами испускания и поглощения устанавливается законом Кирхгофа: всякое вещество поглощает те лучи, которые оно испускает. Этот закон, как мы увидим, не всегда оправдывается и, например, совершенно неприложим к случаю испускания рентгеновых лучей. К спектрам поглощения принадлежит спектр солнца и большинства звезд (см. спектральный анализ в астрономии). В случае испускания линейного спектра число и яркость или интенсивность отдельных линий зависят, между прочим, и от давления лучеиспускающего газа или пара. Однако, Гемфри и Молер (Humphreys и Mohler, 1896) нашли, что и длина волны отдельных линий меняется, хотя и весьма мало, при изменении давления. Когда давление увеличивается от 1 до 12 атмосфер, то длина волны увеличивается на величину порядка 0,01 Å, т. е. происходит маленькое смещение линий налево. Видимая часть спектра обычно изучается визуально, т. е. глазом. Оставляя в стороне лучи Герца, отметим, что инфракрасные лучи спектра изучаются наблюдением того нагревания, которое они вызывают в особых, весьма чувствительных приборах. Сюда относятся термоэлектрические столбики или спаи, особенно в т. н. радиомикрометрах. Кобленц (Coblenz) построил такие приборы со спаями Bi-Pt или Ві—сплав Ві с Sn, настолько чувствительные, что он мог сравнить, например, излучения твердых и светлых пятен на поверхности Юпитера. Весьма чувствительными радиомикрометрами пользовался Рубенс (Rubens), которому принадлежит главная заслуга изучения инфракрасного спектра. Другой способ основан на применении болометра (см. VI, 238). Для изучения ультрафиолетовой части спектра пользуются почти только фотографическим способом, который, впрочем, может служить и для исследования видимого спектра. Им же пользуются при изучении спектра рентгеновых лучей. Другой способ основан на ионизации (ХХII, 659) газов этими лучами. Приборы, которыми пользуются для изучения спектров, имеют различные названия: спектроскопы служат только для рассматривания спектра; спектрометры дают возможность производить более или менее точные измерения, относящиеся к распределению спектральных линий; в спектрографах получается спектр на поверхности светочувствительной пластинки, так что образуется фотография спектра. Все названные приборы могут быть с призмами или с дифракционными решетками. Приборы второго рода имеют то существенное преимущество, что отпадает возможность поглощения лучей внутри того вещества, из которого составлена призма.

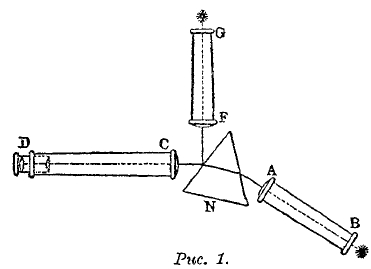
Рис. 1.

Чтобы избежать поглощения лучей воздухом, помещают весь прибор в замкнутый со всех сторон ящик подходящей формы, из которого воздух выкачивается до весьма малого давления. Такой прибор называется вакуум-спектрограф; им пользуются, главным образом, при изучении спектров рентгеновых лучей. Схема простого спектроскопа изображена на рис. 1 в горизонтальном разрезе. N призма из флинтгласа или кварца; А т. н. коллиматор; это трубка, на конце В которой находится вертикальная щель, ширину которой можно менять; перед ней ставится источник, спектр которого желают получить. На конце А находится чечевица с фокусным расстоянием, равным расстоянию АВ; поэтому лучи, исходящие из щели, образуют параллельный пучок, который в призме преломляется и рассеивается. CD зрительная труба, объектив С которой собирает все лучи в фокальной плоскости трубы, и, притом, в зависимости от преломляемости лучей в различных местах этой плоскости, в которой, таким образом, получается горизонтальный спектр, состоящий из такого числа изображений щели Б, сколько различного рода монохроматических (однородных, одного и того же λ) лучей находится в исследуемом потоке видимой лучистой энергии. В случае сплошного спектра число изображений неограниченно велико. Окуляр D служит для рассматривания спектра, FG труба, на конце G которой находится горизонтальная щель, прикрытая стеклянной шкалой с весьма мелкими делениями, освещенная каким-либо ярким пламенем. Лучи, исходящие из этой щели, делаются чечевицей F параллельными; они отражаются боковой поверхностью призмы N и также попадают в трубу, в фокальной плоскости которой получается изображение шкалы над верхним краем спектра. По этой шкале можно определить положение различных светлых или темных спектральных линий и произвести сравнение спектров различных источников. Если источник неудобно поместить перед самой щелью В (например, вольтову дугу), то можно его установить на любом расстоянии и проектировать его изображение при помощи чечевицы на самую щель. Для увеличения дисперсии, т. е. удлинения спектра, что дает возможность точнее рассмотреть все детали, употребляются спектроскопы с целым рядом призм, через которые лучи проходят последовательно, все более и более рассеиваясь. Устраиваются и такие приборы, в которых лучи проходят через ряд призм сперва в одном, а потом в обратном направлении, что приводит к рассеянию как бы от удвоенного числа призм. Хильджер (Hilger) в Лондоне устроил спектроскоп с тремя призмами, через которые лучи проходят по три раза взад и вперед, так что получается действие как бы от 18-ти призм. Весьма удобными представляются прямые спектроскопы (à vision directe), в которых происходит дисперсия без отклонения средних лучей от их первоначального направления. В них имеется сложная призма, состоящая из такого сочетания призм кронгласовых и флинтгласовых, расположенных преломляющими ребрами в противоположные стороны, что те и другие вызывают сами по себе одинаковое отклонение средних лучей.

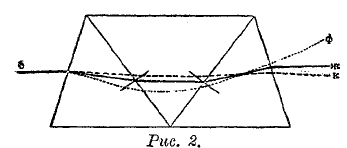
Рис. 2.

При этом, однако, дисперсия, вызываемая призмами, неодинакова; значительно преобладает дисперсия флинтгласовых призм, и этот избыток обнаруживается в окончательном результате прохождения лучей через всю сложную призму. На рис. 2 показан ход лучей в призме Амичи (Amici), которая состоит из трех призм: средней из флинтгласа и двух крайних из кронгласа. На рисунке показан ход лучей красного (к), желтого (ж) и фиолетового (ф). Падает луч белый (б); оказывается, что выходящий желтый луч ему параллелен.

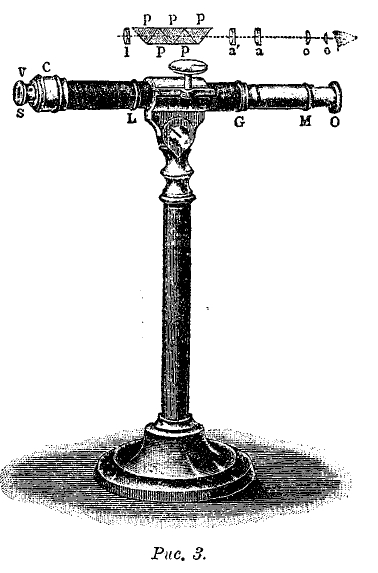
Рис. 3.

На рис. 3 изображен прямой спектроскоп и над соответствующими местами расположение внутренних частей. В SV находится щель, в L чечевица I коллиматора; далее, идет сложная призма (2 флинтгласовые и 3 кронгласовые), сложный объектив а'а и окуляр о'о зрительной трубы.

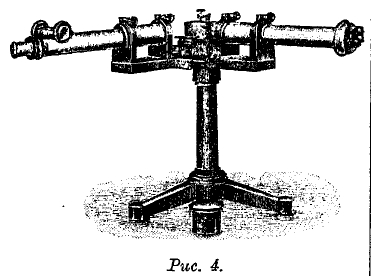
Рис. 4.

На рис. 4 изображен современный спектрометр Хильджера (Hilger) с непосредственным отсчетом длин волн. Спектр получается от дифракционной решетки, соединенной с прямоугольной призмой, от гипотенузы которой лучи отражаются. Коллиматор со щелью (справа) и зрительная труба (слева) установлены неподвижно, между тем как призма и решетка вращаются, так что возможно последовательно провести весь спектр через поле зрения трубы, вращая барабан, который на рис. 4 виден в средней части прибора и на рис. 5 изображен отдельно. На боковой поверхности барабана, расположена винтообразная шкала, проходящая мимо неподвижного указателя. Числа на шкале соответствуют сотням ангстремов, так что отсчеты можно делать с точностью до одного ангстрема. Установка окулярной части зрительной трубы производится вращением кольца, находящегося на средней части трубы, или вращением винта, расположенного над трубой. Колпачок, отдельно изображенный внизу, надевается на барабан, когда прибором не пользуются. Хильджер один только строит также спектрометры со ступенчатыми дифракционными решетками (эшелон), дающими огромную дисперсию. Недостаток этих приборов заключается в том, что дифракционные спектры последовательных высоких порядков m, m + 1, m + 2 и т. д. наложены друг на друга и сдвинуты каждый относительно соседнего на весьма малую величину. Отсюда следует, что ступенчатая решетка может употребляться только для исследования весьма однородных лучей, например для изучения строения отдельных спектральных линий.

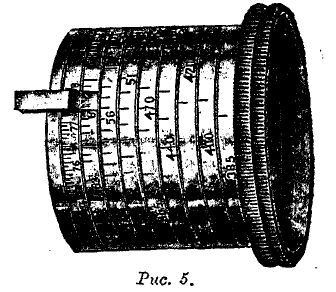
Рис. 5.

Вуд (Wood) устроил отражательные решетки, борозды которых имеют совершенно определенную, с точностью известную геометрическую форму; зная ее, можно предвычислить распределение энергии между дифракционными спектрами различных порядков (см. свет), которые решетка дает справа и слева от средней полосы. Для этого борозды должны быть значительно шире, чем, например, в решетках Роленда (Rowland), так, чтобы форма поперечного сечения этих борозд могла быть тщательно исследована при помощи микроскопа. Борозды должны быть проведены таким снарядом, который придавал бы им желательную геометрическую форму. Сам Вуд проводил борозды на поверхности металлической пластинки, например позолоченной меди, при помощи ребра кристалла карборунда, плоские стороны которого составляют угол в 120°. Таким образом, борозда ограничена двумя совершенно гладкими плоскостями, составляющими угол в 120°. При этом условии углы α и β между этими плоскостями и первоначальной поверхностью пластинки зависят от положения режущего кристалла и могут быть выбраны вполне произвольно при условии α + β = 60, или вообще α + β = 180°—А, где А двугранный угол режущего кристалла. Расстояние b борозд также может быть выбрано произвольно и, например, сделано равным нулю. Отражение происходит от всех одинаково расположенных сторон борозд, например от всех левых или от всех правых, так что эти стороны играют роль щелей решетки. Такая решетка по своему характеру более подходит к ступенчатой, т. е. к эшелону, чем к обыкновенной; поэтому Вуд и назвал ее эшелетой (échelette). Меняя α, β и b, можно, получить желательное, в каждом случае, распределение энергии по дифракционным спектрам различного порядка. Так, Вуд построил эшелету, которая давала следующее распределение всей энергии в процентах: средняя полоса 32, первый спектр справа 40, второй 9, третий 10, первый слева 9. Все остальные спектры содержали ничтожную часть всей энергии, 40% которой было сосредоточено в первом спектре справа. Распределение энергии вдоль сплошного спектра зависит от источника. Для спектра абсолютно черного тела (см. излучение) это распределение определяется формулой Планка (там же, формула (10)). Замечательно, какой огромный процент всей испускаемой лучистой энергии приходится на невидимую, инфракрасную, часть спектра, как это видно из  следующей таблички:

	Энергия видимой части спектра, %	Энергия инфракрасной части спектра, %
Платина при красном калении	0	100
Пламя водорода	0	100
Пламя масла	3	97
Пламя газовое	4	96
Платина при белом калении	4,6	95,4
Лампочка накаливания (уголь)	6	94
Вольтова дуга	10,4	89,6
Ацетиленовое пламя	10,5	89,5
Гейсслерова трубка	32	68
Ртутная лампа	40,9-47,9	59,1-52,1

Распределение отдельных частей спектра, получаемого призмой, зависит от вещества призмы. На рис. 6 изображены три спектра солнца одинаковой длины, полученные от призм из флинта, крона и воды (в треугольном сосуде). Особенно в средней части видно различие в распределении фраунгоферовых линий. Еще большая обнаруживается разница, если сравнить спектры от призмы и от дифракционной решетки, как это видно на рис. 7, где верхний спектр дифракционный, нижний — от призмы, причем красные концы находятся справа. В первом красная, оранжевая и желтая части несравненно более растянуты, чем во втором, между тем как голубая, синяя и фиолетовая части сужены, как это видно, если сравнить положения одинаковых фраунгоферовых линий. Для выражения длин волн различных спектральных линий пользовались до конца восьмидесятых годов системой шведского ученого Онгстрема (Angstroem), в основе которой лежало число λ = 5895,13 Å для желтой линии D₁ паров натрия. Затем вошла в употребление система Роленда (Rowland), в которой исходным числом является более точное λ = 5896,156 Å для линии D₁. Ныне общепринята международная система, при которой все λ выражаются в I·Å (интернациональные ангстремы; мы далее будем опускать букву I); основой служит здесь λ для красной кадмиевой линии, которая принимается равной λ = 6438,4696 I.Å. Это число постановлено уже никогда не менять. Этим вводится новая единица длины I.Å, которая не тождественна с Å = 10^-8 см.

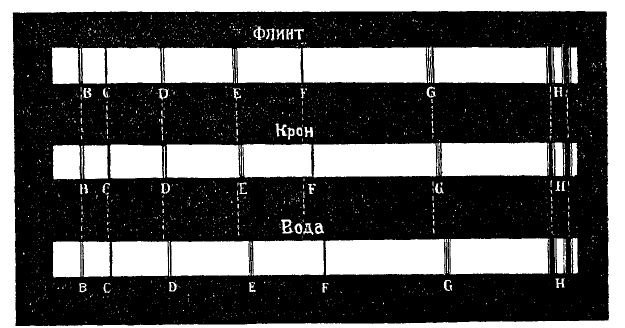
Рис. 6.

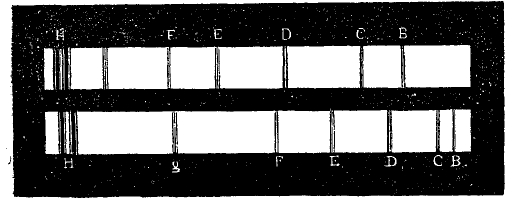
Рис. 7.

Укажем главнейшие спектральные линии некоторых элементов, особенно в видимой части спектра, причем все Х даем в ангстремах. Водород (Н, а не Н₂). В видимой части пять линий; приводим их обозначения, цвет, длину волны и обозначения соответствующих фраунгоферовых линий солнечного спектра.

Обозначение	Цвет	Длина волны	Фраунгоферова линия
Hα	Красный	6563,04	C
Hβ	Зеленый	4861,49	F
Hγ	Синий	4340,66	G’
Hδ	Фиолетовый	4101,85	H
Hε	Фиолетовый	3970,25	H

Кроме этих, имеется еще большое число линий в ультрафиолетовой части и несколько линий в инфракрасной. При особых условиях возникает «многолинейный» спектр водорода, который и в видимой части содержит множество линий (см. ниже). Гелий характеризуется двойной желтой линией D₃ около 5876. Натрий — двойная желтая D₁D₂, разность длин волн D₁ и D₂ около 6 Å. Кадмий. Четыре яркие линии: красная 6438,7, зеленая 5086 и синие 4800 и 4678; в ультрафиолетовой части  ряд линий, из которых последняя имеет λ = 2144,4. Железо. Число линий доходит до 5000. Дальнейшие подробности будут указаны ниже. Немногие спектры, о которых здесь было сказано, относятся к т. н. дуговым спектрам, которые получаются, когда данное вещество лучеиспускает в вольтовой дуге, в гейсслеровой трубке или в пламенах. Иной характер имеют искровые спектры, получаемые при электрическом искровом разряде; подробности см. ниже. Майкельсон (Michelson) первый показал (1892), что многие спектральные линии имеют сложную структуру, т. е. состоят из группы очень близких друг другу линий. Весьма часто одна из линий, основная, обладает большой интенсивностью, между тем как остальные чрезвычайно слабы; последние в этом случае называются спутниками или трабантами. Они изучались многими учеными; ступенчатая решетка (эшелон) дает возможность их непосредственно видеть. Не были найдены спутники в линиях Zn, Al, Mg, Ag, Sn и Ne. Небольшое число линий исследовано, и некоторые найдены со спутниками, у Ві, Сu, Н (красная двойная), Не и Те. Большинство линий просты, но некоторые со спутниками у Со, Са и Рb. У Cd исследованы 6 линий, из которых три оказались со спутниками. Красная линия кадмия 6538,47 не имеет спутников. Много линий со спутниками найдены у Мn и Нg. Совершенно особое положение занимает ртуть, линии которой исследовались многими учеными. Всего было изучено 12 линий, из которых только две, 4916 и 4339, оказались без спутников; в девяти линиях число спутников колеблется от одного до десяти. Исключительный интерес представляет зеленая линия 5461, которая исследовалась многими учеными, нашедшими, что она состоит из 10—12 отдельных линий. Особенность ее заключается в том, что ее нельзя рассматривать, как состоящую из главной линии и из спутников, так как многие ее составные части почти одинаково ярки. Приводим числа, которые дает Яники (Janicki). Здесь 6 обозначает расстояния (в ангстремах) отдельных линий от той из них, для которой λ наименьшее. Относительная яркость указана числами, причем 1 обозначает наибольшую яркость.

δ	0,000	0,134	0,168	0,188	0,214	0,227	0,236	0,245	0,254	0,320	0,364	0,450
яркость	2	5	3	6	1	3	1	1	3	1	4	7

Как видно, 4 линии примерно одинаковой, наибольшей яркости. Расстояния линий друг от друга выражаются сотыми долями ангстрема. Весьма важным представляется вопрос о нормальных линиях. Международная Комиссия по исследованию солнца (International Union for Cooperation in Solar Research) постановила пригласить ученых всех стран способствовать построению системы нормальных спектральных линий, длины волн которых были бы определены с величайшей достижимой точностью (по возможности до 0,001 Å), и которые затем служили бы для сравнения с ними длин волн других спектральных линий. В основу положена нормаль первого порядка, а именно уже упомянутая красная кадмиевая линия, длину волны которой определяли Майкельсон (Michelson) в Америке и затем совместно Беноа, Фабри и Перо (Benoit, Fabry, Perot) во Франции. Она (см. выше) установлена равной 6438,4696 I.Å. Первая задача Комитета заключалась в установлении нормалей второго порядка, которые, по постановлению комиссии, должны быть распределены по возможности равномерно по всему спектру и отстоять друг от друга не более, чем на 50 Å. Эту работу произвели Бюссон и Фабри (Buisson, Fabry), Эверсгейм (Eversheim), Пфунд (Pfund) и др. Из них Эверсгейм пользовался еще зеленой кадмиевой линией 5085,822, которая у него играла роль второй основной линии. На основании этих работ комитет установил, прежде всего, первую серию 58 нормальных  линий второго порядка, расположенных между 4282,408 и 6494,993 Å; между ними только 3 линии марганца, одна никеля и одна висмута, все остальные линии (53) принадлежат железу. Позже комитет утвердил вторую серию нормалей второго порядка, всего 34 линии, из которых 2 линии никеля, а все остальные — железа. Из них 27 линий находятся между 4233,615 и 3370,789 Å; их большая часть принадлежит ультрафиолетовому спектру. Всего установлены 92 нормали второго порядка. Нормали третьего порядка должны отстоять друг от друга на расстояниях от 5-ти до 10-ти I.Å. Их определением занялись многие ученые, но узаконенного ряда еще не существует. Между прочим, Бернс (Burns) измерил 131 ультрафиолетовую линию между 2851 и 3701. Обращаемся к фундаментальному вопросу о закономерностях в спектрах. В истекшем столетии задача спектрального анализа сводилась к возможно полному описанию спектров испускания и поглощения всевозможных веществ, т. е. к определению длин волн и относительных яркостей линий спектров, а также их зависимости от состояния этих веществ. Многие ученые пытались открыть какие-либо закономерности в распределении линий спектра данного элемента. Эти попытки впервые увенчались успехом в 1885 г., когда Бальмер (Balmer, преподаватель гимназии в Базеле) нашел, что видимые линии водорода Н весьма точно выражаются формулой, которую можно представить в виде

в которой n волновое число (см. выше) и R т. н. постоянная Ридберга (Rydgerg), которая для водорода Н равна

Потом оказалось, что для всех линий от k=3 до k=29 формула (3) дает n с поразительной точностью. С момента открытия Бальмера началась новая эра в истории спектрального анализа. Вскоре обнаружилось, что линии спектра ионизированного гелия Не удовлетворяют подобной же формуле

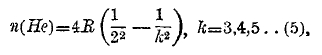
где, однако, R(Не) немного больше R (Н), а именно:

Впоследствии Ридберг открыл, что для спектральных линий всех остальных элементов существуют формулы, в которых встречается один и тот же множитель

Все линии, волновые числа которых определяются одной какой-либо формулой, составляют т. н. спектральную серию, а сами формулы называются сериальными. Последовательные линии одной серии, если идти слева направо, все более и более сближаются и, наконец, становятся настолько близкими друг другу, что их разъединить невозможно; они образуют хвост серии, который имеет резкую границу. Первая, т. е. головная линия водородной (бальмеровской) серии (3) и есть линия На (см. выше) при λ=6563,04. Предел хвоста (k=∞) находится при n=R(H):4, т. е. при λ=3647,0 в ультрафиолетовом. Вместо (5) можно написать более общую формулу

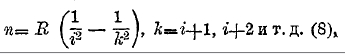
где i постоянное целое число, но различное для различных серий; при і=2 мы имеем серию Бальмера. При і = 1 получается другая водородная серия

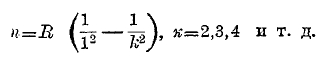
Она вся расположена далеко в ультрафиолетовой части; ее головная линия находится при λ = 1215,7, предел хвоста (k = ∞, n = R) имеет длину волны λ = 911,75. Затем имеется серия i = 3; ее формула

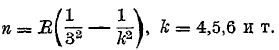
д. Вся серия расположена в инфракрасной части; первые ее две линии, головную 18751,3 и вторую 12817,5, нашел Пашен (Paschen), а три или четыре дальнейшие открыл Брэкет (Brackett, 1922); предел (n = R:9) находится у λ = 8025,75. Наконец, Брэкет открыл 2 линии серии

головная линия находится при λ = 2,63μ (26300 Å), конец хвоста (k = ∞, n = R:16) при λ = 1,459μ. Дальнейшие серии (i=5,6,7 и т. д.) не открыты; они должны лежать в отдаленной инфракрасной части спектра. В спектре ионизированного гелия удалось все линии распределить по сериям вида

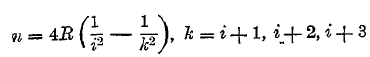
и т. д., где R дано в (6). В настоящее время удалось найти серии в спектрах большого числа элементов, причем число серий может быть весьма различное. Эти серии имеют следующие названия: I. Первая побочная серия, еще называемая резкой. II.Главная серия. ІІІ. Вторая побочная серия, еще называемая диффузной. IV. Серия Бергмана. V. Третья побочная или ультрабергмановская серия. Последняя и дальнейшие серии лишь редко наблюдались, но с их существованием приходится считаться при объяснении некоторых комбинационных линий (см. ниже). Серия (3) водорода — первая побочная; серия i=1 представляет главную серию. Спектральные серии бывают трех родов: состоящие из одиночных линий, из дублетов (по две линии) и из триплетов (по три линии). В системе серий, названия которых были приведены, все линии всех серий имеют один и тот же характер, т. е. они все одиночные или дублеты или триплеты. Иногда в спектре находятся несколько систем серий, причем в одной системе серий все линии могут быть, например, дублетами, а в другой триплетами. Сериальные формулы элементов имеют, если исключить H и Не, более сложный вид, чем (8). Их можно представить в общем виде:

где i и k целые числа, причем для всех линий одной серии i одно и то же, а k = i+1, i+2 и т. д. Две функции F₁(i) и F₂(k) почти одинаковые, так что мы их могли бы обозначить одной буквой F. Так как они все-таки не вполне одинаковы, то возможен и редкий случай k=i. Во всех случаях эти функции содержат множитель R, см. (7); в этом заключается великое открытие Ридберга, в честь которого R и называется постоянной Ридберга. Для водорода F(i) = R:i², для гелия F(i) = 4R:i², где, однако, эти R несколько отличаются от (7), см. (4) и (6). Ридберг предложил для F₁(i) выражение вида R:(i + μ)², а F₂(k) = R:(k+σ)², где μ и σ величины постоянные для всех линий одной серии, но неодинаковые для различных серий. Риц (Ritz) дал для F₁(i) формулу вида

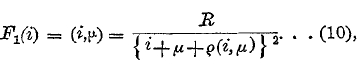
где (i, μ) или просто іμ общепринятый сокращенный символ. Здесь μ и q постоянные числа для всех линий одной серии, причем q величина весьма малая. В знаменателе стоит сама величина (i, μ). Для F₂(k) имеется подобное же выражение, но μ и q имеют другое численное значение. Формула (9) показывает, что волновое число n равняется разности двух величин, которые называются термами. В спектрах многих элементов были открыты линии, которые не входят в состав имеющихся спектральных серий. Риц первый высказал мысль, что каждый отдельный терм имеет как бы самодовлеющее существование и значение, так что можно взять два терма из двух различных серий и, образовав их разность, получить волновое число n спектральной линии, которая, как оказывается, во многих случаях, но далеко не всегда, действительно существует. Это знаменитый комбинационный принцип Вица. Таким образом, и получаются упомянутые несериальные линии, которые называются комбинационными линиями. Истинный физический смысл термов будет выяснен ниже на основании учения Бора (Bohr) о строении атомов. Мы теперь можем сказать, что каждая спектральная линия определяется двумя термами, разность которых дает волновое число, соответствующее этой линии; длина волны определяется затем формулой (2). Можно написать:

где (i, μ) постоянный, а (k, μ') переменный терм сериальной формулы. Для перечисленных выше серий (главной, побочных и т. д.) имеются определенные обозначения типа (i, μ), см. (10), но, к сожалению, различные авторы пользуются неодинаковыми обозначениями. Речь идет о том, как обозначить добавочную величину μ' во втором терме, который содержит переменное число k Приводим табличку этих обозначений.

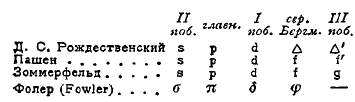
Мы будем пользоваться обозначениями Зоммерфельда (Sommerfeld), так что вторые термы в сериальных формулах сокращенно обозначаются: (k, s), (k, р), (k, d), (k, f), и (k, g). Оказывается, что в первых, постоянных термах величина μ имеет те же самые значения s, р, d, f и g, как и во вторых, но в другом порядке. Окончательно сериальные формулы имеют такой вид (меняем порядок):

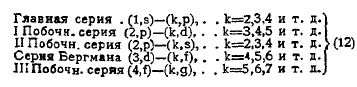
В английских книгах серия Бергмана называется фундаментальной (fundamental series, отсюда буква f). Числа s, p, d, f, g быстро убывают в указанном порядке; так, например, для искрового спектра магния s = 0,93, р = 0,31, d = — 0,045, f = 0,0006. Чем меньше эти числа, тем менее данный терм отличается от бальмеровского R:k², т. е. тем более он «водородоподобен». При k=∞ вторые термы исчезают; поэтому первые термы определяют волновое число края, т. е. конца хвоста серии. Так как s и р часто больше 0,5, многие авторы прибавляют 0,5 к числам і или k. Они пишут для главной серии (1,5s) — (k,р), где к = 2, 3, 4 . . , а для II побочной

Из формул (12) вытекает ряд следствий, из которых мы приводим немногие. Прежде всего, оказывается, что во всех сериях одиночных линий существуют только следующие термы (пишем упрощенно):

Формулы (11) выражают следующие закономерности: I. Две побочные серии имеют один и тот же предел (2, р). II. Этот предельный терм (2, р) равен второму терму головной линии главной серии. Дублетные и триплетные серии бывают двух родов. А. Разность Δn двух волновых чисел линий дублетов, а также разности Δ₁n и Δ₂n трех волновых чисел линий триплетов одни и те же для всех дублетов или триплетов серии, которая имеет два или три предела. В. Разность Δn или Δ₁n и Δ₂n постепенно уменьшается, доходя в пределе до нуля. Вся серия имеет общий предел. В самое последнее время (1923) стали играть большую роль мультиплетные серии, каждый член которых состоит из большого числа отдельных линий (спектр неона, железа и др.). В сериальных формулах прибавляют числовые индексы, чтобы отличить друг от друга отдельные линии дублета, триплета и т. д., например, р₁, р₂, р₃. И здесь имеется ряд закономерностей, относящихся к случаю, когда серии состоят из дублетов или триплетов. I. Главная серия всегда второго рода (один предел). II. Две побочные серии всегда первого рода и одинаковой кратности (дублеты или триплеты). III. Разности Δn или Δ₁n и Δ₂n в обоих побочных сериях одни и те же. IV. Распределение относительных яркостей спектральных линий во всех дублетах или триплетах одной и той же серии одинаковое. V. Терм, содержащий букву s, см. (12), всегда одиночный (обозначения s₁, s₂ и т. д. не существуют). Когда первый терм двойной или тройной, то серия, очевидно, первого рода (несколько пределов); в сериях второго рода второй член двойной или тройной. Усложнение получается, когда оба терма двойные или тройные: тогда получаются сложные дублеты из трех линий и сложные триплеты из шести линий. Когда мы имеем дело с комбинационными линиями, термы которых взяты от одиночных линий и от дублетов или триплетов, то в термах одиночных линий пишутся большие буквы S, Р, D и т. д., например, Sp₂, Pd₃, p₂D и т. д. Принцип комбинации ограничен знаменитым принципом отбора, который говорит, что при нормальных условиях возможны только такие комбинации, при которых в двух термах стоят соседние буквы ряда s, р, d, f, g. Однако, при особых условиях, например, при действии электрических сил, этот принцип нарушается. Имеются следующие закономерности: I. Не существуют комбинации между термами дублетов и термами одиночных линий или триплетов. II. Существуют комбинации между термами одиночных линий и термами триплетов. В полосатых спектрах также найдены разного рода закономерности, главным образом Деландром (Deslandres). По спектру поглощения можно произвести качественный, а иногда и количественный анализ поглощающей среды, например, какого-либо раствора. Ультрафиолетовый спектр был расширен Шуманном (Schumann, 1901) примерно до λ=1000Å. Значительный дальнейший шаг удалось сделать Лайману (Lyman, 1915), который пользовался дифракционной решеткой. Источником служила кварцевая разрядная трубка с электродами из Mg, АІ, Fe и Ca. Он дошел до 510 Å. В этой новой «лаймановской» области он обнаружил весьма большое число линий водорода, гелия и аргона. Не останавливаемся на описании опытов Ричардсона и Бацони (Richardson, Bazzoni, 1921), которые косвенным способом доказали, что спектр гелия тянется, примерно, до λ=420, а спектр водорода до λ = 900. Замечательное исследование произвел Милликен (Millikan, 1919—1921), которому удалось чисто оптическим способом расширить ультрафиолетовый спектр и открыть в новой области огромное число спектральных линий различных элементов. Вся его установка находилась в высоком вакууме (10^-4 мм. Нg). Источником служила весьма сильная разрядная искра от индукционной катушки и от батареи лейденских банок. Наиболее важное усовершенствование представляли вогнутые дифракционные решетки, в которых число черточек доходило до 1100 на 1 мм. Фотографическая пластинка не содержала желатины, которая поглощает крайние ультрафиолетовые лучи. Обзор всех полученных им результатов Милликен опубликовал в 1924 г. Он нашел более 800 линий между λ = 1862 и λ = 136,6 Å; последнее число относится к линии алюминия. Весьма важно, что он не нашел ни одной новой линии водорода, длина волны которой была бы меньше длины волны предельной линии

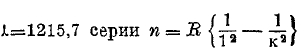
(см. выше). Для He и Li также не нашлось новых линий. Весьма малые λ он нашел в спектрах Fe, Ni, Zn, Na ,Мg и АІ. Относительно инфракрасного спектра уже было упомянуто, что Рубенс (умер в 1922 г.) и его сотрудники дошли до Я = 343 у = 0,343 мм. В 1921 г. Рубенс построил три дифракционные решетки, состоящие из тонких, параллельно друг другу натянутых медных проволок, толщина которых равняется 1,004, 0,483 и 0,196 мм, и ими исследовал, между прочим, спектр ртутной дуговой лампы, который содержит лучи наибольшей достигнутой длины волны. Между инфракрасными лучами наибольшей длины волны (0,34 мм) и лучами Герца наименьшей длины волны (4 мм) остается неисследованный промежуток, примерно в 3 ½  октавы. Рубенс упоминает о работе Байера (Ваеуеr), который достиг длины волны λ=2 мм, но эта работа нигде не напечатана; если ее принять во внимание, то неизученная часть все же обнимала 2 ½  октавы. Никольс и Тир (Nichols, Tear, 1923) смогли точно измерить длину волны луча λ = 1,8 мм, а также «обертон», получаемый при электрических колебаниях, для которых λ = 0,9 мм. Эта работа уменьшила неизученную часть до 1,5 октав. Однако, последние упомянутые работы все же не дают возможности действительно получить спектр между 4 мм  и 1 мм и изучить его свойства. М. А. Левитская (в Ташкенте) обнаружила лучи этой промежуточной области; но она могла напечатать лишь предварительное сообщение, и работа осталась неоконченной, вследствие ее отъезда из Ташкента. Замечательное исследование произвела А. А. Глаголева-Аркадьева (в Москве) по способу, предложенному В. К. Аркадьевым. Чтобы получить электрические лучи высокой частоты, она построила «массовый вибратор,» изображенный на рис. 8. В стеклянный сосуд А помещена однородная смесь металлических опилок и машинного масла, образующая вязкую массу, которая непрерывно перемешивается мешалкой В. В эту массу погружалась небольшая часть карболитового колесика К, вращающегося при помощи мотора. Колесико захватывает массу, так что на нем появляется как бы шина, верхняя часть которой непрерывно сменяется при вращении колесика. Две проволоки fи f¹ подводят к этой шине высокое напряжение от индуктора, причем разряды происходят через вибрационную массу, в металлических частицах которой возникают электрические колебания, а следовательно и лучи соответствующей частоты. Получается одновременно большое число лучей с различными частотами, так как опилки имеют неодинаковые размеры, и к основным тонам примешиваются обертоны с удвоенной, утроенной и т. д. частотами. Исследование возникающего общего весьма сложного колебания обнаружило между его составными частями лучи, для которых λ колебалось от 50 мм до 81,8μ, так что они распределялись по всей неисследованной области и далеко проникали в уже известную инфракрасную часть. Можно надеяться, что усовершенствование этого метода даст возможность получить монохроматические лучи (одного λ) и изучить их свойства.

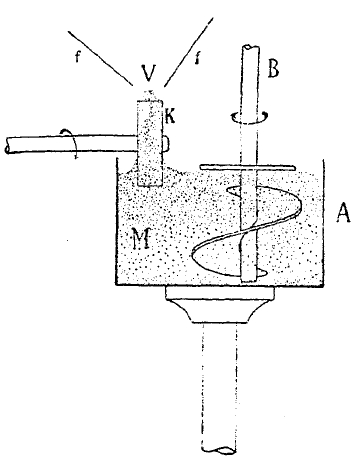
Рис. 8. Источник излучения — массовой излучатель.

Мозли (Moseley) показал (1913), что при помощи рентгеновых лучей можно определить порядковый номер Z всех элементов системы Менделеева. Так, для водорода Z=1, гелия Z=2, лития Z=3 и т. д. до урана Z=92. Пусть v частота колебаний какого-либо луча из спектра лучистой энергии; тогда величина h_v, где h постоянная Планка (Planck, 1900), называется квантом лучистой энергии данной частоты v или длины волны λ = с:v, где с скорость света. Величина h размера энергии (или работы), помноженной на время. Ее численное значение h = 6,54 10^—27эрг.·сек. По теории Планка (см. излучение) атомы поглощают и испускают лучистую энергию только целыми квантами. Теория относительности приводит к результату, что масса m движущегося тела зависит от его скорости v по формуле

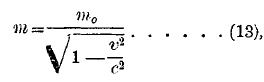
где m₀ масса покоящегося тела, с скорость света. Эта формула имеет большое значение в случае движения электронов, скорость которых во многих случаях соизмерима со скоростью с света. Заряд е электрона и его масса m₀, по опытам Милликена (Millikan), равны

Лучи Рентгена получаются при ударе электронов катодного луча в антикатод. Если V разность потенциалов катода и антикатода, то скорость v электронов в момент удара определяется формулой eV = ½ mv² из которой получается, если не обращать внимания на (13), т. е. принять m=m₀, на основании (14) достаточно точно

если V выражать в вольтах. Общепринято выражать скорость v электронов в вольтах. Когда электрон ударяется в поверхность антикатода, то его энергия ½ mv² = еV превращается в один квант hv рентгеновского луча. Таким образом, имеем

Подставив е и h, и заменив v через с:λ, где с скорость света, получаем

Таким образом, может быть найдена длина волны λ рентгеновского луча в ангстремах, если известна разность потенциалов между катодом и антикатодом в вольтах, т. е. напряжение, действующее в рентгеновой трубке. При сравнительно небольших скоростях V (в вольтах!) электронов, получается непрерывный («белый», см. выше) спектр рентгеновых лучей. При определенных скоростях V появляются части линейного спектра рентгеновых и притом сразу целые группы линий. Чем меньше λ, тем меньше лучи Рентгена поглощаются при прохождении через материю. Лучи, мало поглощаемые, называются жесткими, более поглощаемые — мягкими. Лучи, образующие сплошной спектр, называются рассеянными, а лучи, дающие линейный спектр — характеристичными для данного элемента. Они появляются, если этот элемент входит в состав антикатода (например, сплав) или в состав того вещества, которым антикатод покрыт. Говоря просто о рентгеновском спектре какого-либо элемента, подразумевают спектр характеристический. Особенность этого спектра заключается в следующем. Спектр в инфракрасной, видимой, и ультрафиолетовых частях имеет для каждого элемента свой особый вид. Число спектральных линий, их расположение и относительная интенсивность весьма различны для различных элементов. Все элементы имеют в известных, но весьма широких пределах совершенно одинаковые рентгеновские спектры;  число, относительное расположение и относительная яркость линий не зависят от лучеиспускающего вещества. Поэтому можно вообще говорить о «рентгеновском спектре», о его структуре, не называя вещества, дающего этот спектр. Влияние этого вещества сказывается только на том положении, которое вся совокупность спектральных линий занимает на общей спектральной шкале лучистой энергии. Это значит, что длины волн рентгеновых лучей зависят от лучеиспускающего элемента, причем эта зависимость простая: чем больше порядковое  число Z элемента, тем более его рентгеновский спектр отодвинут в сторону   уменьшающихся длин волн, тем более  жестки все лучи. При переходе от   одного элемента к другому весь  спектр, как целое, перемещается в ту  или другую сторону. Мозли открыл и закон этого смещения: корень квадратный из частоты v колебаний для  каждой линии есть линейная функция порядкового числа Z элементов. Спектр рентгеновых лучей состоит из нескольких групп близких друг другу линий; отдельные группы весьма далеки друг от друга. Эти группы получили в порядке убывающей жесткости названия К, L, М и N. Расстояние групп К и L доходит до нескольких октав. Так, например, для вольфрама группа K расположена между 178 Х (0,178 Å) и 213 Х, группа L между 1025 Х и 1675 Х, группа М между 6066 Х и 6973 Х (6,973 Å). Не все 4 группы существуют или могли наблюдаться у всех элементов. Группа К исследована для всех элементов от Na (Z =11) до Pt (Z = 78); группа L от Fе (26) до U (92); группа М от Dy (66) до U (92); группа N известна только для Ві (83), Th (90) и U (92). Для элементов от Nа (11) до Мn (25) известны только линии Х; все три группы K, L и M найдены для немногих элементов от Dy (66) до Pt (78). Не все линии данной группы могли быть фактически наблюдаемы во всех элементах, вообще имеющих эту группу; иногда они слишком слабы, иногда они лежат вне пределов возможных наблюдений. Группа K состоит из 4-х главных линий и около 8-ми очень слабых; последние находятся только в спектрах легких элементов от Nа (11) до V (23). Длины волн колеблются от 11883 Х (11,889 Å) у Na до 158,2 Х у Pt. Кроме того, Дессауер и Бак (Dessauer, Back, 1919) нашли для U (92) две линии 154 Х и 104 Х = 0,104 Å; последнее число представляет наименьшую (наиболее жесткий луч) из наблюдавшихся до сих пор длин волн рентгеновых лучей (если не считать лучей γ, см. выше). Группа L содержит до 23 различных линий, которые все имеются у вольфрама. Длины волн этих линии колеблются для различных элементов от 0,597 Å (Ur) до 17,66 Å у Fе (26). Последнее число дает наибольшую (наиболее мягкий луч) из известных длин волн рентгеновых лучей. Группа М была открыта Зигбаном (Siegbahn, 1916); Хялмар (Hjalmar, 1923) нашел до 17-ти линий у Ur. Длины волн расположены между 2,248 Å (Ur) до 9,323 (Dy). Группу N открыл Делейзек (Delejsek, 1922); Хялмар нашел у Ur и Th по 5-ти линий, для которых λ находится между 8,691 Å и 13,805 Å и одну линию у Ві с длиной волны

λ = 13,208 Å.

До 1913 г. задача спектрального анализа заключалась в изучении спектров испускания и поглощения всевозможных веществ. В настоящее время эта задача заменилась совершенно другой, гораздо более глубокой: определить для каждой спектральной линии механизм ее возникновения, т. е. то изменение, которое происходит внутри атома, когда он испускает лучистую энергию, дающую эту линию. Постановка и постепенное решение этой задачи стали возможными только после того, как датский ученый Бор (Niels Bohr, 1913) создал свое учение о строении атома. Необходимо здесь напомнить основы этого учения. Атом любого элемента, порядковое число которого Z, состоит из ядра, вокруг которого вращаются электроны, подобно тому, как планеты вращаются вокруг солнца, и по тем же законам Кеплера. Число вращающихся электронов равно порядковому   числу Z. Положительный заряд, эквивалентный электрону, называется «протон»; таковым является ядро атома водорода. Пусть А атомный вес элемента, который, после работ Астона (Aston) об изотопах, считается за число целое. Ядро состоит из А протонов, в которых сосредоточена почти вся масса атома, и из (А—Z) электронов, так что общее число электронов в нейтральном атоме также равно Z. Вокруг ядра атома водорода (один протон) вращается один электрон. Ядро атома гелия (А = 4, Z = 2), тождественного с частицей α, испускаемой многими радиоактивными веществами, состоит из 4 протонов и 2 электронов; вокруг этого ядра вращаются два электрона. Вокруг ядра атома лития (А=7, Z=3, 7 протонов и 4 электрона) вращаются три электрона и т. д. Вокруг ядра атома цинка (Z = 30) вращаются 30 электронов; наконец, вокруг ядра атома урана (Z = 92) вращаются 92 электрона. Ядро действует, как положительный заряд Е=Ze, где е заряд электрона, рассматриваемый как величина положительная, т. е. заряд протона. Учение Бора построено на трех постулатах. Из них первый относится к орбитам электронов; эти орбиты Бор считает за круговые. Постулат утверждает, что не все орбиты, т. е. радиусы орбит, возможны, а лишь некоторые, удовлетворяющие определенному условию. Пусть a₁, а₂, а₃... a_k... радиусы возможных орбит в возрастающем порядке, так что а₁ радиус орбиты, ближайшей к ядру. Постулат первый: движение электронов может совершаться только по таким орбитам, на которых момент количества движения электрона равен целому кратному от h:2π, где h постоянная Планка. Это дает равенство

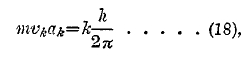
где v_k скорость электрона на k-той возможной орбите; k целое число, m масса электрона. Классическая электродинамика учит, что электрон, движущийся с ускорением, безразлично —  тангенциальным или нормальным, должен непрерывно испускать лучистую энергию насчет энергии своего движения. Бор вводит постулат второй: когда электрон движется по одной из возможных орбит, удовлетворяющих условию (18), то он вовсе не лучеиспускает. Пусть J_k энергия атома, когда электрон находится на k-той орбите. Оказывается, см. ниже, что J_k тем больше, чем больше k. Пусть i < k, тогда J_i < J_k. Когда электрон перескакивает или «падает» с k-той орбиты на i-тую, то атом теряет энергию J_k—J_i. Постулат третий: когда электрон падает от одной возможной орбиты на другую, лежащую ближе к ядру, то энергия, потерянная атомом, переходит в одну кванту лучистой энергии, испускаемой атомом в этот момент. Пусть v частота колебаний в испускаемом луче. Тогда

Эта формула дает возможность вычислить частоту, а затем и длину волны испускаемого луча. Обратный переход электрона, т. е. поднятие электрона с i-той орбиты на k-тую, возможен только при внешнем воздействии, сопряженным с притоком энергии. Таким воздействием может служить приток извне лучистой энергии, одна кванта которой тратится на соответствующее изменение энергии атома, причем формула (19) остается в силе. Другой случай воздействия мы имеем, когда свободно движущийся электрон ударяется в атом. В этом случае

где е заряд, V скорость электрона (в вольтах); v частота того луча, который испускается при обратном падении электрона с k-той на i-тую орбиту; длина волны этого луча определяется формулой (17). Когда электрон поднят с его нормальной орбиты на одну из «выше» лежащих возможных, то атом называется возбужденным; если же электрон выброшен за пределы атома, то последний называется ионизированным. Ионизация может быть простая, двойная, тройная и т. д., смотря по числу потерянных электронов; при этом пользуются обозначениями вроде Не⁺, Li⁺⁺, Be⁺⁺⁺ и т. д. Воспользоваться формулой (19) возможно только в случае, когда вокруг ядра движется только один электрон, ибо уже при двух электронах мы имеем неразрешимую «задачу трех тел» небесной механики, и величины E_k и E_i не могут быть вычислены. Поэтому нижеследующее относится только к случаю одного электрона, вращающегося вокруг ядра, т. е. к водороду Н и ионизированному гелию Не⁺; Li⁺⁺, Be⁺⁺⁺ еще не удалось получить. Для круговой орбиты мы имеем (сила равна массе на ускорение)

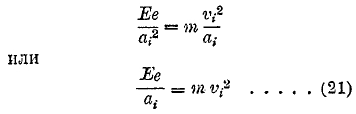
Формулы (21) и (18), в которые надо вставить i вместо k, дают возможность определить а_i и v_i; для Н заряд ядра Е = е, для Не⁺ имеем Е = 2е. Затем легко вычислить энергии I_i и І_k и по формуле (19) частоту, которую напишем в виде V_ki или волновое число n_kvi = v_ki:c, где с скорость света. Если считать ядро неподвижным и вообще его заряд Е=eZ, где Z порядковое число элемента, то этим путем получается для волнового числа формула не вполне точная. Ядро также движется, а именно вращается около центра инерции ядра и электрона; оказывается, что если принять во внимание движение ядра, то в формуле для волнового числа прибавляется множитель М:(М + m), где М  масса ядра, m масса электрона. Этот множитель равен 1840:1841 для водорода, 7360:7361 для Не⁺. Окончательная формула:

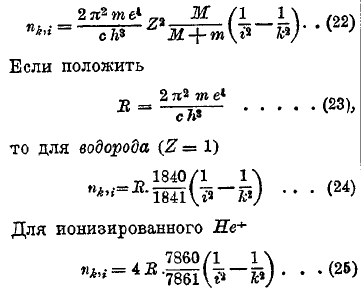
Если в (24) подставить численные значения величин m, e, c и h то получается как раз постоянная Ридберга (7). Таким образом, постоянная Ридберга, появляющаяся в формулах спектральных серий, оказалась выраженной через массу и заряд электрона, скорость света и постоянную Планка! В этом заключался первый из великих результатов учения Бора. Множитель М:(М + m) можно принять равным единице для всех элементов после гелия. Сравнивая (24) и (25) с (3) и (5), мы видим, что R (H) = 1840/1841 R, R (Не) = 7860/7861 R, а это дает R (Не) = 1,00041 R(H)  в полном согласии с (6). Итак, теория Бора не только вполне объяснила, почему для Н и Не постоянная Ридберга немного меньше, чем для других элементов, но и вполне точно определила отношение этих ее двух значений. В этом заключался второй поразительный результат учения Бора. По внешнему виду формулы (24) и (25) вполне соответствуют формулам (3) и (5), если в первых двух считать i постоянным и k = і+1, i+2, i+3 и т. д. Этим объяснено и происхождение спектральных серий: серия спектральных линий получается, когда электроны падают на одну и ту же i-тую возможную орбиту от различных вышележащих k-тых (k > i) орбит, на которые они были подняты при возбуждении атома. Серия Бальмера (і = 2), см. (3), получается, когда электроны падают на вторую орбиту с 3-ей, 4-ой и т. д., и то же самое относится к серии (5) гелия. Ультрафиолетовая серия водорода n = R (1/i² – 1/k²) возникает, когда электроны падают на первую орбиту, а две инфракрасные серии, о которых выше было сказано — когда электроны падают на третью и на четвертую орбиты. В каждой серии яркость линий убывает, если идти от головной линии (k = і+1) к хвосту. Это объясняется тем, что наблюдаемая яркость спектральных линий зависит от числа атомов, претерпевших ту степень возбуждения, которая должна подготовить испускание лучей соответствующей длины волны. Слабое возбуждение (k небольшое) более вероятно и потому чаще происходит, чем сильное (k большое) возбуждение, вследствие чего и обратные небольшие падения (k—і небольшое) чаще встречаются, чем падения большие. Бор предположил, что электроны движутся по круговым орбитам. Зоммерфельд (1916) ввел движения по эллипсам, на которых скорость электрона меняется. Принимая во внимание формулу (13), Зоммерфельд (1916) мог вполне объяснить происхождение спутников спектральных линий водорода и гелия и теоретически предсказать их расположение. Пашен (Pasehen) на опыте подтвердил правильность предсказаний Зоммерфельда. В атомах, содержащих более одного электрона вне ядра, т. е. от двух (гелий) до 92-х (уран), все электронные орбиты могут быть разделены на так называемые электронные слои, как бы обхватывающие друг друга, причем, однако, орбиты одного слоя могут проникать в слои, лежащие ниже, т. е. ближе к ядру атома. Эти слои обозначаются, если идти от ядра, буквами Е, L, М, N, О, Р, Q. Общее число электронов в атоме (вне ядра) равняется порядковому числу Z элемента в периодической системе Менделеева. Если идти вдоль этой системы от Н до Ur, то каждый следующий элемент получается из предыдущего добавлением одного электрона и соответствующего изменения в ядре. Таким образом, происходит постепенное построение слоев. Число электронов в окончательно построенных слоях следующее:

К  L  М  N  О  Р  Q

2  8  8 18 18 32  6

Эти числа с точностью соответствуют числам элементов в семи периодах системы Менделеева. Электроны во внешнем слое, построение которого не закончено, называются валентными, от них зависят химические свойства элементов. К валентным электронам относится все то, что было сказано относительно случая, когда вокруг ядра вращается всего только один электрон (Н, Не⁺). Для валентных электронов существуют также, кроме нормальных, еще ряды возможных орбит, на которые эти электроны переходят при возбуждении атомов. Когда один или несколько электронов выбрасываются за пределы атома, то это дает простую, двойную и т. д. ионизацию атома. Когда один из валентных атомов переходит от одной из возможных орбит на другую, лежащую ниже, то происходит лучеиспускание согласно формуле (19), и возникают спектральные серии, причем каждая серия соответствует переходам электронов к одной и той же нижней (i-той) орбите от различных выше лежащих (k-тых) орбит. Точное вычисление энергий E_k и Е_i сделать невозможно, если число вращающихся электронов больше одного. Однако, Зоммерфельду удалось, путем введения некоторых упрощенных представлений относительно действия на валентный электрон остальных частей атома, вывести для терма формулу, совершенно совпадающую с формулой (10). Таким образом было объяснено появление добавочных величин s, р, d, f, g и общий вид сериальных формул (12). Комбинационный принцип Рица и самостоятельное значение отдельных термов делаются понятными, если принять во внимание, что по теории Бора каждый терм равняется определенному значению энергии атома, соответствующему определенному положению электрона на одной из возможных орбит. Электроны каждого слоя делятся на подгруппы, кроме слоя К. Слой L содержит 2 подгруппы, слой М—3, N—4 подгруппы, слой О должен бы содержать 5 подгрупп, а Р—6 подгрупп, но даже в атоме урана они имеют только по 3 подгруппы, а слой О, вместо семи, только одну группу. Подгруппа может содержать до 8-ми электронов. Для благородных газов последняя подгруппа внешнего слоя содержит 8 электронов; она как бы заполнена; валентных электронов нет и потому газы химически недеятельны (гелий сюда не относится). Число валентных электронов, содержащихся во внешнем, еще не готовом слое, равно номеру той группы периодической системы, к которой элемент принадлежит. Это число равно 1 для щелочных, 2 для щелочноземельных металлов и т. д.; оно равно 7 для галоидов. Мы видели, что для каждого элемента следует отличать спектры дуговой и искровой. Между линиями того и другого никогда не наблюдаются комбинации, т. е. не существует сочетаний термов, принадлежащих двум различным спектрам. По мнению, впервые высказанному Бором и ныне общепринятому, дуговой спектр получается от нейтрального атома, искровой же от атома ионизированного, т. е. уже потерявшего один из электронов внешнего слоя. В первом случае один из валентных электронов был поднят на одну из возможных орбит. При этом оставшаяся часть атома должна действовать на удалившийся электрон приблизительно так, как один положительный заряд +е в ядре, так что получается нечто, напоминающее атом водорода. В числителе терма стоит постоянная Ридберга R. Этим объясняется некоторое сходство между дуговым спектром щелочных металлов (один внешний валентный электрон) и спектром водорода. Во втором случае один из электронов выброшен из атома, а другой поднят на одну из возможных орбит. Этот электрон находится под влиянием, которое, в грубом приближении, равно влиянию заряда + 2 е в центре атома. Атом напоминает в этом случае атом ионизированного гелия Не⁺. В числителе термов приходится писать 4 R вместо R. Особенно должно существовать сходство между спектрами щелочноземельных металлов (два валентных атома) и спектром гелия. В 1919 г. Зоммерфельд и Коссель (Kossel) высказали закон смещения: искровой спектр всякого элемента, по своему общему характеру, одинаков с дуговым спектром предыдущего в периодической системе элемента, т. е. порядковое число которого на единицу меньше, а, следовательно, число электронов, окружающих ядро, также на единицу меньше. Элемент и предыдущий ему принадлежат соседним группам периодической системы, причем первую и последнюю (щелочные металлы и благородные газы) также следует считать за соседние. Когда атом элемента подвергся ионизации, т. е. потерял один электрон, то его внешний слой, от которого, прежде всего, зависит характер спектра, делается одинаковым по числу электронов со внешним слоем атома предыдущего элемента. Остается разница в составе и строении ядра и, в связи с этим, и в расположении электронных орбит. Это, очевидно, вполне объясняет закон смещения и невозможность существования комбинационных линий. Заметим, что щелочные металлы (группа I) имеют дуговые спектры из дублетов, щелочноземельные (группа II а) из одиночных линий, дублетов и триплетов, а благородные газы дают спектры, состоящие из огромного числа линий. Искровой спектр щелочных металлов действительно состоит из огромного числа линий, т. е. он похож на многолинейный дуговой спектр предыдущего благородного газа. В 1923 и 1924 годах появились работы, в которых произведены подробные сравнения искровых спектров калия, рубидия и цезия, соответственно со спектрами аргона, криптона и неона. При искровом разряде усиливаются дублеты в спектре щелочноземельных металлов. Оказывается, что термы дублетов Mg, Са, Sr, Ва имеют множитель 4 R (как у Не⁺), откуда и следует, что эти дублеты принадлежат ионизированным атомам. Наконец, оказалось, что искровой спектр земель АІ и Sc содержит триплеты, аналогичные триплетам дугового спектра Мg₂ и Са. Предыдущее может служить иллюстрацией того, что выше было сказано о современной задаче спектрального анализа: указать механизм возникновения всего того, что наблюдается в спектрах испускания и поглощения. Такой же иллюстрацией послужит и все нижеследующее. В спектрах газов и паров наблюдаются части непрерывного спектра, который начинается там, где кончается хвост серии, и тянется в сторону убывающих длин волн (направо). Теория Бора дает им следующее объяснение. Сериальные линии определяются равенством (19): Е_k—Е_i = hv. Мы получаем край хвоста, когда электрон падает от «предела атома», т. е. весьма удаленной орбиты (k = ∞), на ту i-тую, которой определяется данная серия. Положим,  что для этого края Е_k = Ē, так что Ē — Е_i = hv. Однако, может случиться, что ионизированный атом улавливает какой-либо из свободно движущихся электронов, вырванных из других атомов. Такой электрон может обладать произвольной скоростью v, а следовательно и энергией ½ mv². Если этот электрон остановится на i-той орбите, то увеличение энергии атома будет равняться

и будет испускаться луч, частота v' которого определится равенством

Отсюда

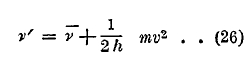
Так как v не подвершено никаким условиям, то v’ может иметь какие угодно значения, которые больше v, чем и объясняется возникновение непрерывного спектра, начинающегося у края хвоста спектральной серии. Это объяснение приложимо, например, к ионизированным атомам водорода и натрия. Другой случай непрерывного спектра мы имеем у галоидов, внешний слой которых имеет (см. выше) семь электронов. Атомы галоидов имеют большое «сродство» к электронам, т. е. стремление заполнить внешний слой восьмым электроном. Вот этот-то восьмой электрон может присоединиться к атому галоида, причем испускается луч, частота  которого зависит от случайной энергии этого электрона, вследствие чего и возникает непрерывный спектр. Таковой спектр нашел Штейбинг (Steubing) в парах йода. Различные закономерности, которые относятся к спектрам поглощения газов и паров, также объясняются теорией Бора. Так, например, невозбужденные газы поглощают лучи только той серии, которые испускаются при переходах электрона от вышележащих орбит на орбиту нормальную. Но когда атомы газа возбуждены и валентный электрон уже находится на i-той орбите, то притекающая извне лучистая энергия может быть затрачена на поднятие электрона от i-той орбиты на какую-либо k-тую, где k > i. В этом случае спектр поглощения содержит линию той серии спектра испускания, которая получается при падениях электронов на i-тую серию. Возможен также сплошной спектр поглощения, когда притекающая лучистая энергия выбрасывает электрон за пределы атома, причем этот электрон может еще приобрести произвольно большую живую силу. Формула, аналогичная (26), объясняет происхождение сплошного спектра поглощения. Полосатые спектры получаются при лучеиспускании молекул. И здесь общие основы теории Бора многое разъяснили, но возможность полной математической теории сильно уменьшена тем обстоятельством, что нам неизвестно строение хотя бы простейшей молекулы Н₂. Тем не менее теория смогла указать на общий механизм возникновения полосатых спектров и объяснить главнейшие из относящихся к ним закономерностей. Для молекулы следует отличать три рода движений: 1. вращение молекулы; 2. вибрационное движение атомов, входящих в состав молекулы; 3. движение электронов. Общего поступательного движения всей молекулы рассматривать не приходится. Каждое из трех интрамолекулярных движений может подвергаться изменениям. При вращении может, прежде всего, меняться угловая скорость; затем также и ось вращения, когда число атомов в молекуле больше двух. Вибрации могут быть гармонические или, особенно при больших амплитудах, сложные, разлагающиеся на ряд гармонических (ряд Фурье). Изменение в движениях электронов может заключаться в том, что электроны переходят от одних возможных орбит к другим, или меняется расположение и форма орбит. Каждое из трех изменений вызывает изменение общей энергии молекулы. Если эта энергия уменьшается от J₂ до J₁ то испускается луч, частота v которого определяется, как для отдельного атома, формулой J₂ — J₁ = hv. Та же формула дает частоту поглощаемого луча, когда притекающая извне лучистая энергия тратится на увеличение энергии молекулы от J₁ до J₂. Ряд обстоятельств усложняет весь вопрос. Прежде всего, легко сообразить, что каждое изменение одного из трех движений вызывает изменение двух остальных. Так, например, при изменении угловой скорости вращения меняются расстояния между атомами, а это должно влиять на частоту вибраций и на распределение электронных орбит. Бьерум (Bierrum, 1912), Шварцшильд (Schwarzschild, 1916) и др. развили теорию полосатых спектров, исходя из таких соображений. Подобно тому, как возможны лишь электронные орбиты, удовлетворяющие условию (18), так и угловые скорости ω вращения молекулы не все возможны, а только те, при которых момент количества движения вращающейся молекулы равен целому числу h:2π, где h постоянная Планка. Пусть К момент инерции, тогда

где i = 1, 2, 3 и т. д. дает возможные угловые скорости. Для ротационной энергии имеем

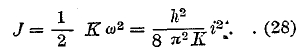
Когда вращение скачком меняется от k-той угловой скорости к i-той, то вышеприведенная формула дает

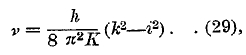
если допустить, что момент инерции не изменился. При постоянном i и k = i +1, і + 2, і + 3... получаем ряд линий, для которых частоты вида v = а + bk², что соответствует формуле, которую дал Деландр для полосатых спектров. Линии (29) составляют так называемый ротационный спектр, который наблюдался некоторыми учеными в далекой инфракрасной части (до λ = 100μ), особенно для паров воды. Изменение вибраций можно рассмотреть только для случая двуатомной молекулы. Когда меняются одновременно и вращения, и вибрации, то получается ротационно-вибрационный полосатый спектр, сравнительно легко наблюдаемый в близкой инфракрасной (λ равно нескольким μ) или даже в видимой части. Водород и гелий могут дать многолинейные спектры. Их происхождение то же, что и в полосатых спектрах, но в водороде линии так сильно раздвинуты, что полосы не образуются. Спектр же гелия представляет ясный переход к полосатым спектрам. Изучение полосатых спектров двуатомных газов дает возможность определить расстояние r атомов друг от друга и момент инерции К. Так, для НСІ получилось r = 1,26·10^-8 см, К = 2,6·10^-40 гр.см². Вопрос об энергии вращения молекул играет большую роль в учении о теплоемкости газов и паров. Таким образом, открылась глубокая, неожиданная связь между такими, казалось бы, далекими друг от друга отделами физики, как спектральный анализ и учение о теплоемкости! С рентгеновым спектром новая теория справилась гораздо полнее, чем со спектрами инфракрасными, видимыми и ультрафиолетовыми. Причина заключается в сравнительной простоте рентгеновского спектра, который (см. выше) один и тот же для всех элементов; меняется только его положение на общей шкале спектра лучистой энергии. Учение о механизме возникновения рентгеновых лучей основано на следующем. Выше было сказано, что электроны, окружающие ядро атома, распадаются на слои К, L, М, N, О, Р, Q, причем число «готовых» слоев тем больше, чем больше порядковое число Z элемента. Валентные электроны наружного слоя могут двигаться по различным возможным орбитам, причем энергия атома зависит от той орбиты, по которой движется валентный электрон. Эти орбиты можно поэтому рассматривать, как поверхности уровня энергии. Оказывается, что и во внутренних, готовых электронных слоях существуют вполне определенные поверхности уровня, причем каждому уровню соответствует определенная энергия атома. Число уровней в различных слоях следующее:

Эти уровни обозначаются, в порядке возрастающей энергии, следующим образом: слой К, уровень К; слой L, уровни L₃, L₂, L₁; слой М, уровни М₅, M₄, М₃, M₂, M₁ слой N, уровни N₇, N₆, … N₁; слой О, уровни O₅, O₄, ... О₁; слой Р, уровни Р₃, Р₂, Р₁. Вся теория рентгеновых лучей основана на следующем положении: рентгеновы лучи возникают, когда электрон одного из внутренних готовых слоев, находящийся на определенном уровне энергии, выбрасывается до пределов или за пределы атома. Исходный уровень удобно изобразить общим символом А_i, где А одна из букв К, L, М и т. д., и і один из числовых индексов, возможных для данного слоя. Вырванный из уровня А_i  электрон не может остановиться на каком-либо уровне одного из вышележащих внутренних слоев, так как все эти слои заполнены электронами, все места заняты. Он, пожалуй, может остановиться на внешнем слое, если этот слой еще не заполнен; но в большинстве случаев он вылетит за пределы атома. Это выбрасывание может быть произведено, во-первых, ударом электрона, движущегося со скоростью V вольт, см. (15), как, например, в рентгеновых трубках, в которых V есть разность потенциалов катода и антикатода; во-вторых, при поглощении атомом одного кванта рентгеновых лучей, притекающих извне, как это происходит при возникновении вторичных рентгеновых лучей. Рентгеновский характеристичный спектр состоит (см. выше) из групп линий, которые мы обозначим буквами К, L, М и N, т. е. теми же, как и электронные слои атома. Когда электрон вырван из слоя А и притом от уровня А_i, то на освободившееся место может перескочить электрон от одного из выше лежащих слоев В, от уровня B_k. Пусть А_i и B_k обозначают не только уровни энергии, но и значения энергии, соответствующие этим уровням. Тогда при падении электрона возникает рентгеновский луч, частота v которого определяется из равенства

Одинаковость обозначений (К, L, М, N и т. д.) слоев и групп рентгеновых лучей основана на следующем: когда электрон выбрасывается из слоя К, то при падении электронов от вышележащих слоев L, М, N и т. д. возникают рентгеновы лучи К; когда электрон вылетает из слоя L, то при падении электронов из слоев М, N, О и т. д., возникают рентгеновы лучи L. Аналогично происходит возникновение лучей М и N. Не безразлично от которого из трех уровней слоя L, пяти, уровней слоя М и т. д. был отнят электрон, ибо на этот уровень падают электроны от уровней вышележащих.  Каждый рентгеновский луч характеризуется, таким образом, двумя уровнями энергии двух различных внутренних электронных слоев атома. Точное указание двух уровней для каждого из рентгеновых лучей представляет задачу систематики этих лучей. Эту задачу можно в настоящее время считать вполне решенной. В связи с этим находится рациональный метод обозначения самих рентгеновых лучей. До недавнего времени эти лучи обозначались весьма неудобно греческими, буквами с приставкой числовых или иных индексов, причем различные авторы пользовались неодинаковыми обозначениями. Кроме того, приходилось для каждого луча добавлять указание на группу К, L и т. д., так как одни и те же обозначения α, α₁, β, β₁ и т. д. встречались во всех группах. Теперь рентгеновский луч обозначается простым указанием характеризующих его двух уровней энергии. При этом безразлично, символ которого из двух уровней энергии ставить первым и который вторым, так как электрон всегда переходит от вышележащего уровня к нижележащему, причем второй определяет и ту группу (К, L и т. д.), к которой принадлежит обозначаемый луч. Можно, например, написать обозначение лучей L₁M₂, M₂O₄ или М₂L₁, O₄М₂. Ясно, что в первом случае электрон переходит от уровня М₂ к уровню L₁, и луч принадлежит группе L; во втором случае электрон переходит от уровня О₄ к уровню М₂, и луч взят из группы М. Понятно, почему все элементы, имеющие достаточно большое порядковое число, дают вполне одинаковый спектр рентгеновых лучей. Происходит это от того, что внутренние законченные слои, в которых эти лучи возникают, в атомах этих элементов построены одинаково. Когда в рентгеновой трубке постепенно увеличивать скорость V (в вольтах)  электронов катодного луча, ударяющих в антикатод, то все лучи группы K появляются сразу. Это объясняется тем, что при достижении V такой величины, при которой вырывается один из двух электронов слоя K, в имеющихся налицо атомах, число которых мы считаем огромным, начинается падение электронов от различных вышележащих уровней, вследствие чего и появляются сразу все лучи K. В слое L находятся три уровня L₃, L₂ и L₁; с увеличением скорости V сперва выбрасывается электрон из уровня L₁ (энергия наименьшая); требуется большая энергия, чтобы выбросить электрон из слоя L₂, и еще большая — из слоя L₃. Поэтому лучи L должны появляться последовательно тремя группами, если постепенно увеличивать V, что в действительности и наблюдается. В рентгеновских спектрах замечаются дублеты линий с одинаковой разностью чисел колебаний v₁, они особенно тщательно изучены в спектре лучей L. Их происхождение двоякое. Во-первых, в слое L находятся два уровня энергии L₁ и L₂, ясно, что если от какого-либо одного из вышележащих уровней А_i падают электроны на эти уровни, то получаются две линии, для которых разность частот не зависит от исходного уровня А_i. Второго рода дублеты получаются, когда от двух различных уровней А_i и A_k одного и того же из слоев М, N, О и т. д. падают электроны на один и тот же уровень слоя L_i. Весьма важно, что не существует рентгеновского спектра поглощения в смысле закона Кирхгофа, т. е. соответствующего спектру испускания. И этот факт легко объясняется. Линия спектра испускания A_iB_k получается при падении электрона от уровня B_k на освободившееся место уровня А_i. Когда через слой данного вещества проходят «белые» рентгеновские лучи, то та же самая линия была бы поглощена при поднятии электрона от уровня А_i к уровню B_k. Но такое поднятие невозможно, так как слой В весь заполнен, и в нем нет свободного места. Внешняя притекающая энергия может быть израсходована только на выбрасывание электрона до предела или за предел атома. Непрерывный спектр рассеянных (см. выше) рентгеновых лучей получается при скоростях V электронов, которые недостаточны, чтобы вызвать лучи характеристические. Этот спектр отнюдь не исчезает, когда последние появляются, так что линейный спектр всегда выступает на фоне спектра непрерывного. Этот последний имеет резкий край со стороны убывающих длин волн (справа). По мере увеличения скорости V, длина волны λ_m, этого края передвигается дальше направо. Дуан и Гунт (Duane, Hunt, 1916) нашли закон смещения этого края; он выражается формулой

Происхождение непрерывного спектра и этот закон смещения края объясняются очень просто, если допустить, что при ударе электрона часть его энергии теряется и переходит в одну кванту рентгеновского луча. Тогда мы имеем равенство

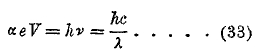
где с скорость света и α правильная дробь. Так как α никаким условиям не подвержена, то при данном V получаются всевозможные λ, которые и дают непрерывный спектр. Когда α = 1, т. е. вся энергия электрона превращается в кванту лучистой энергии, мы получаем еV = hc:λ_m, т. е. Vλ_m = hc:e. Вставив численные значения h, с и е, получаем формулу (17). Выражая V в киловольтах, имеем

V (киловольт) λ_m(Å) = 12,345 . . (34), а это и выражает закон смещения края (32). Все изложенное ясно показывает, как успешно спектральный анализ ныне решает свою новую задачу: разъяснить механизм возникновения всевозможных спектров и тех закономерностей, которые в них наблюдаются.

ЛИТЕРАТУРА. Н. Kayser, «Handbuch d. Spektroskopie», 6 т., Leipzig, 1900—1912; Нильс Бор, «Три статьи о спектрах и строении атома», П., 1923; Sommеrfeld, «Atombau und Spektrallinien», 4-е изд., 1924; Э. Резерфорд, «Строение атома и искусственное разложение элементов», 1923; А. Fowler, «Report on Series of line spektra», London, 1922; W. М. Hicks, «Treatise on the analysis of spektra», Cambridge, 1922; F. Paschеn u, R. Götze, «Seriengesetze d. Linienspektren», Berlin, 1922 (табл.); R. Pohl,  «D. Physik d. Röntgenstrahlen», Braunschweig, 1912; У. Х. Брагг и У. Л. Брагг, «Рентгеновские лучи и строение кристаллов», пер. Г. В. Вульфа. М., 1916; М. Siegbahn, «Spektroskopie d. Röntgenstrahlen», Berlin, 1924; R. Ledoux-Lcbard ct А. Danvilliers, «La physique  des rayons Х.», Paris, 1921; Е. Marx, «Handbuch d. Radiologie», т. V, стр. 151—688, 1919; М. dе Broglie, «Les Rayons Х.», Paris, 1922; G. W. С. Каус, «Х—Rays». 4-е изд., London, 1923.

О. Хвольсон.