Степень (математическая)

Степень (математическая), первоначально означала произведение нескольких одинаковых множителей:

при этом а называется основанием, а n показателем степени, действие называется возвышением в степень. Обратное действие (определение числа, которое после возвышения в данную степень дало бы данное число) называется извлечением корня (см.). Для того, чтобы умножить степень с одинаковым основанием, достаточно сложить показатели:

Отсюда совершенно естественным путем обобщения мы приходим к отрицательным степеням:

Для возвышения степени в степень нужно перемножить показатели, так что (а^m)^p = а^mp. Отсюда естественно возникают дробные степени:

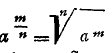
От отрицательных и дробных степеней можно непосредственно перейти к показательной функции а^х, где х обозначает уже любое число, и к решению показательных уравнений b=а^х, иначе говоря, к определению такого показателя х, чтобы а^х равнялось данному числу b; х называется логарифмом (см.) числа b при основании а. Современное обозначение степени было введено Декартом, хотя зачатки его встречаются у Стевина.

В. Кс.