Строительное дело. I. Строительная механика

Строительное дело. I. Строительная механика разрабатывает методы рационального расчета инженерных сооружений. Под расчетом сооружений подразумеваются приемы, позволяющие путем тщательного учета всех условий работы данного сооружения определить те предельные потребные для этого сооружения размеры его, которые могут обеспечить ему длительную и безопасную службу. В своих методах строительная механика опирается на данные сопротивления материалов (см.), каковая наука в свою очередь черпает свои основоположения из законов теории, упругости (см. упругость). Однако, в то время как обе названные науки, особенно теория упругости, подходят к вопросу абстрактно и главную свою задачу полагают в установлении законов упругих явлений, строительная механика трактует свои темы конкретно и дает реальные приемы расчета инженерных сооружений разного рода.

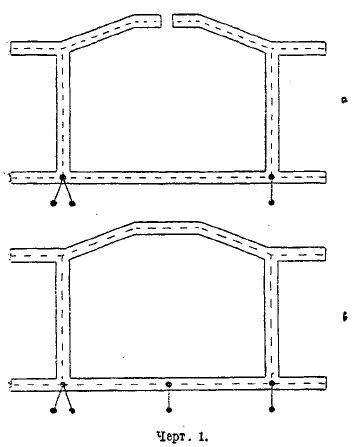
Черт. 1.

В огромном большинстве своем инженерные сооружения могут рассматриваться, как составленные из более или менее сложного сочетания брусьев, т. е. тел удлиненной призматической формы с постоянным или переменным поперечным к оси тела сечением и с длиной оси, значительно превышающей поперечные размеры тела. Брусья, как элементы сооружений, исчерпывающе изучены теорией сопротивления материалов, и это позволяет строительной механике весьма точно проводить расчеты брусчатых систем.

Инженерные сооружения, поскольку они могут быть подведены под брусчатые системы (об особых видах инженерных сооружений — не брусчатых — будет упомянуто в конце настоящей статьи), классифицируются следующим образом:

А. Системы с жестким соединением брусьев между собой в узлах (рамы).

В этих системах отдельные брусья связываются между собой в узлах настолько жестко, что углы между конечными участками осей сходящихся брусьев представляют собой величину постоянную и не меняющуюся под действием внешних сил. Такие системы (рамы) могут быть плоскими или пространственными, в зависимости от того, расположены ли все брусья системы в одной плоскости, или нет. На черт. 1 и 2  показаны типы плоской и пространственной рам.

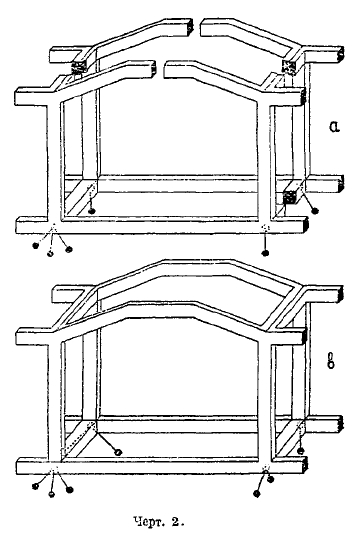
Черт. 2.

Б. Системы с шарнирным соединением брусьев между собой в узлах (формы). В этих системах отдельные брусья, как правило, представляют собой прямые стержни, которые в углах связаны универсальными и идеальными (т. е. работающими без трения) шарнирами, позволяющими отдельным сходящимся стержням под действием внешних сил немного изменять углы между своими осями и оставаться благодаря этому — при действии внешних сил в узлах — прямыми, между тем как в рамах неизменность углов взаимного прилегания брусьев заставляет эти брусья под действием внешних сил, приложенных в узлах, изгибаться. Здесь также возможны плоские и пространственные типы, и примеры их показаны на черт. 3 и 4. Есть еще один признак, по которому можно классифицировать системы: отсутствие или наличие распора в опорах сооружения, т. е. горизонтальной силы, распирающей берега, или, при отрицательном  распоре, стремящейся их сблизить. По этим признакам системы (плоские) делятся на балочные (безраспорные), арочные — с положительным распором и висячие — с отрицательным (черт. 5).

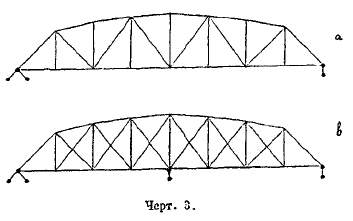
Черт. 3.

На ряду в классификацией по конструктивному признаку, системы классифицируются еще по характеру их работы, а именно могут быть:

I. Системы статически определимые.

II. Системы статически неопределимые.

Классификация одинаково относится и к рамам, и к фермам.

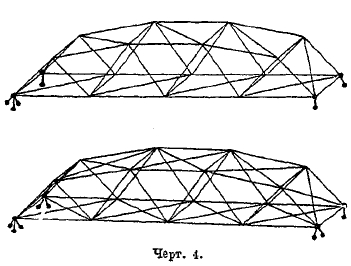
Черт. 4.

Статически определимыми являются такие системы, в которых определение величин: а) внешних реактивных сил, развивающихся в опорах и уравновешивающих собой внешние активные силы, и б) внутренних упругих сил, развивающихся в элементах сооружения и своей внутренней упругой работой уравновешивающих работу внешних сил — производится на основании уравнений статического равновесия сил, т. е. основано на предположении, что тело сооружения можно рассматривать, как идеально твердое тело, действие на которое внешних сил подчиняется законам статики. Для этого необходимо соблюдение некоторых  условий:   

1) опоры должны быть так сконструированы, чтобы число составляющих реактивных сил, которые по этим опорам действуют и своим действием уравновешивают внешние активные силы, равнялось трем на плоскости и шести в пространстве. Опоры всегда условно обозначаются в виде того или иного сочетания прямых жестких стерженьков, снабженных по концам идеальными шарнирами. На черт. 8 и 6а изображены типы плоских и пространственных опор. Для статической определимости сооружения относительно опор необходимо на плоскости иметь сочетание одной двухстержневой шарнирной неподвижной опоры и одной одностержневой шарнирной подвижной. В пространственном случае необходимо иметь одну опору трехстержневую (шарнирно-неподвижную), одну — двухстержневую (шарнирно-подвижную, обеспечивающую движение по прямой) и одну —  одностержневую (шарнирно-подвижную, обеспечивающую движение по некоторой плоскости) или иную эквивалентную комбинацию шести стержней. При таком устройстве опор, очевидно, что трех и, соответственно, шести (в пространстве) уравнений равновесия вполне достаточно для нахождения сил, действующих по опорным стержням.

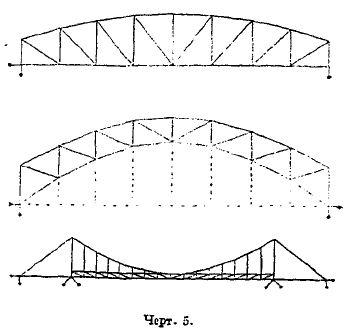
Черт. 5.

2) Стержни и брусья, образующие систему, должны быть так скомбинированы, чтобы в рамах любая часть сооружения могла быть отделена от остального сооружения одним разрезом (т. е. чтобы не было замкнутых контуров), и чтобы в фермах любой разрез, делящий ферму на две части, пересекал на плоскости три, а в пространстве шесть стержней (не более и не менее). В этом случае, как в раме, так и в ферме, искомые внутренние упругие силы в любом месте и в любом стержне определяются при помощи трех и, соответственно, шести уравнений статики путем приравнивания внешних сил в отсеченной части внутренним силам в разрезе, ибо для рамы в каждом сечении следует определить лишь N_z, Q_y и M_x на плоскости и N_z, Q_у, M_z, M_x, M_y в пространстве (см. сопротивление материалов), т. е. как раз три или шесть величин, а для фермы следует определить лишь три или шесть осевых усилий по перерезанным стержням. Применяемые здесь уравнения статики имеют обычный вид:

∑x = 0; ∑y = 0; ∑z = 0;

∑M_x = 0; ∑M_y = 0; ∑M_z = 0;

На черт. 1—4 верхние рисунки изображают статически определимые случаи. В этом случае искомые внутренние силы в разрезах могут рассматриваться, как искомые усилия по некоторым внутренним упругим связям, и таким образом мы всегда ищем усилия по некоторым стержням и по некоторым связям, также эквивалентным некоторым стержням.

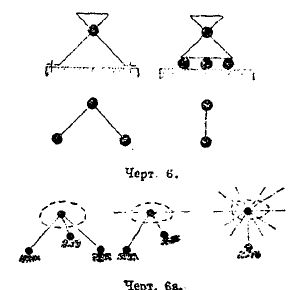
Черт. 6. Черт. 6а

Статически неопределимыми являются такие системы, в коих определение внешних реактивных сил или внутренних упругих сил не может быть произведено по законам статики, так как число неизвестных внешних реактивных или внутренних упругих сил больше того числа, которое соответствует числу уравнений статики — имеются «лишние неизвестные».

По отношению к внешний реактивным силам этими лишними неизвестными являются все опорные стержни сверх вышеописанных трех или шести «классических», а по отношению к внутренним упругим силам лишними неизвестными являются: в рамках — те внутренние силы, которые подлежат определению для размыкания замкнутых контуров; в фермах — осевые усилия тех стержней, которые имеются в системе сверх необходимого числа, обеспечивающего статическую определимость системы. Таким образом, получается ряд лишних стержней и ряд лишних связей.

Для нахождения всех этих лишних неизвестных мы пользуемся тем общим положением, что упругая энергия системы стремится к минимуму, поскольку эта энергия зависит от статически неопределимых величин (принцип Мопертюи, применяемый в строительной механике в виде теоремы Кастильяно).

Так как выражение упругой энергии может быть всегда написано в функции поперечных размеров брусьев, внешних сил и тех же «лишних неизвестных» (общее выражение этой энергии (см. сопротивление материалов), то в нашем распоряжении, при n лишних неизвестных (X₁, X₂, … X_n), получается n уравнений типа:

∂T/∂X₁ = 0; ∂T/∂X₂ = 0; ∂T/∂X_n = 0.

Уравнения эти линейны относительно неизвестных, ибо упругая энергия есть функция квадратичная относительно внешних сил (см. сопротивление материалов), а ее производные по этим силам очевидно линейны, что, впрочем, вытекает и из закона Гука — закона независимости действия сил (см. также сопротивление материалов).

На черт. 1 — 4 нижние рисунки изображают статически неопределимые случаи.

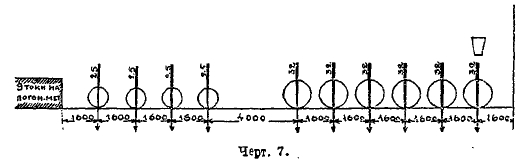
Черт. 7.

Статически определимые и статически неопределимые системы пользуются одинаковым правом гражданства в применении их к инженерным сооружениям. Первые рассчитываются проще, несколько проще по самой своей конструкции и не страдают от случайных осадок опор и от температурных воздействий, но зато менее жестки, более подвижны и менее амортизируют динамическую нагрузку; вторые — требуют для своего расчета предварительного знания всех поперечных размеров отдельных брусьев, имеют иногда довольно сложную конструкцию и почти всегда страдают от осадок опор и от воздействия температуры, но зато их перемещения значительно меньше, и они являются хорошими амортизаторами нагрузки. Практика последних десятилетий равно широко применяет и те и другие системы. Некоторые строительные материалы по самым свойствам своим особо хорошо конструируются в статически неопределимые системы, например, железобетон.

Расчет сооружения начинается с установления тех нагрузок, которые могут действовать на сооружение во время его службы. Наиболее серьезной является нагрузка железнодорожным поездом, имеющая место в сооружениях, возводимых на железных дорогах. Поезд состоит из паровоза, тендера и длинного ряда груженых товарных вагонов. Современные паровозы достигли громадных размеров — на черт. 7 показана схема паровоза, принятого для расчета железнодорожных мостов СССР на особо ответственных линиях в 1921 г. Схема эта в 1925 г. немного изменена, путем придания всем 10 осям одинаковой нагрузки в 30 тонн и снижения погонной вагонной нагрузки с 9 t/m до 8 t/m. Однако, уже в 1922 г. на железных дорогах Соединенных Штатов Северной Америки обращались паровозы с нагрузкой на каждую ось около 40 тонн, и имелись товарные вагоны с погонной нагрузкой в 12 тонн на погонный метр железнодорожного пути. Таким образом, русские нормы в 30 тонн на ось и в 8 тонн на погонный метр превзойдены уже на 33—50%. Нагрузка на оси автомобилей грузовиков доходит уже до 20 тонн на каждую ось.

Строительная механика не считает, однако, целесообразным предусматривать при расчете слишком отдаленные, имеющие быть примененными в данной стране лишь через много лет нагрузки, во-первых, потому, что предвидеть размеры таких нагрузок заранее невозможно, и во-вторых, потому, что инженерные сооружения имеют ограниченный самими свойствами материала срок службы, и за исключением каменных сооружений, которые могут стоять веками, сооружения из других материалов работают нормально не более пяти-шести десятков лет.

По норме НКПС амортизационный срок службы каменных сооружений определяется в 75 лет, металлических и железобетонных — 50 лет.

Кроме подвижной переменной нагрузки, сооружение несет на себе свой собственный вес, величина которого определяется по предварительным соображениям на основании данных о весе существующих сооружений того же рода. Отношение веса полезной нагрузки, (к которой относится вся нагрузка сверх собственного веса) к сумме весов полезной нагрузки и собственного называется иногда «коэффициентом полезного действия».  Величина этого коэффициента особенно характерна для железнодорожных мостов. При малых «пролетах», т. е. при малых расстояниях между опорами, коэффициент достигает 0,80—0,70, а при пролетах, равных  150 метрам, он уже близок к 0,50 и оказывается даже ниже этой цифры при пролетах, близких к 200 метрам. Таким образом, большие пролеты оказываются экономически невыгодными, так как сооружение в этом случае работает, главным образом, на свой собственный «мертвый» вес. В очень больших мостах вес полезной нагрузки падает до 10—15% веса моста.

Действие внешних сил иа сооружение комбинируется при расчете самым наивыгоднейшим образом, так как подвижность полезной нагрузки допускает разные ее комбинации, причем наилучшим средством для изучения этих возможных комбинаций внешних сил являются так называемые инфлюентные линии, или линии влияния, предложенные в средине прошлого столетия германскими инженерами Винклером и Кульманом и введенные в русскую инженерную практику в конце XIX в. профессором Л. Д. Проскуряковым (умер в 1926 г.). Линии эти графически изображают закон изменения какой-либо исследуемой в данном сооружении величины при перемещении единичной подвижной нагрузки по сооружению и могут быть применены к изучению как подвижной, так и неподвижной нагрузок.

В последние годы построение этих «линий влияния» опирается на принцип взаимности, высказанный еще во второй половине прошлого века английским ученым Максвеллом (Maxwell) и выражающийся в том, что инфлюентная линия какой-либо величины может быть легко, получена, как фигура перемещения всех точек сооружения, которая могла бы иметь место при устранении того опорного стержня или той внутренней связи, работу  которой мы хотим изучить, и при замене этого стержня или этой связи силой (на опорном стержне) или парными силами (на внутренней связи)  по величине равными единице.

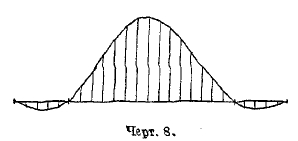
Черт. 8.

Так, построение иифлюентной линии опорной реакция какой-либо из опор четырехпролетной неразрезной балки (черт. 8) может быть осуществлено путем отбрасывания соответственного опорного стержня, в данном случае третьего слева, и замены его силой, равной единице, действующей на данное, лишенное одного из своих опорных стержней сооружение. Масштабом, определяющим то значение ординат достроенной от данной силы фигуры перемещений балки, которое превращает эту фигуру в искомую инфлюентную линию, является значение той ординаты перемещения, которая получается по направлению груза, равного единице, приложенного к нашему сооружению в освобожденном от стержня или связи месте. Измеренная в этом масштабе каждая ордината инфлюентной линии указывает, какое именно влияние единичный груз, стоящий в данной точке, оказывает на изучаемую величину.

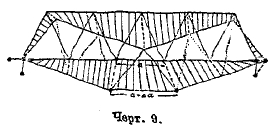
Черт. 9.

На черт. 9 аналогичное построение даст инфлюентную линию для среднего элемента нижнего пояса шарнирно-стержневой формы, позволяющую одновременно учесть влияние нагрузки как верхних, так и нижних узлов.

Система инфлюентных линий, оценивающих работу всех важнейших элементов сооружения, позволяет без труда найти при данной нагрузке те условия работы сооружения в целом, которые являются наивыгоднейшими, т. е. наиболее опасными и для всего сооружения и для его отдельных частей, и придать сооружению и всем частям его такие размеры которые, отнюдь не  будучи излишними, обеспечивали бы безопасную работу сооружения.

В сложных статически неопределимых случаях построению системы инфлюентных линий предшествует  раскрытие статической неопределимости, для которого, как выше уже было указано приходится решать ряд линейных уравнений типа:

формула

В этих уравнениях отдельные буквы имеют следующие значения:

X₁, X₂,…, X_n -  искомые неизвестные усилия по опорным стержням или по внутренним связям.

Р – данные внешние силы.

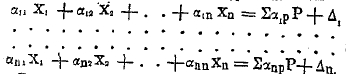
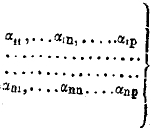
Перемещение точки приложения той или иной из неизвестных сил Х под влиянием сил, стоящих в точках приложения сил X₁, X₂,…, X_n или сил Р, и имеющих значение, равное единице, причем первый значок указывает место изучаемой точки, а второй – местоположение действующей силы.

∆₁, ∆₂,…, ∆_n, - наперед  заданные перемещения могущие иметь место по направлению того или иного из опорных стержней или той или иной из внутренних связей.

В целом каждое уравнение выражает ту мысль, что перемещения сооружения в опорных точках или по направлению внутренних связей должны быть равны наперед заданным величинам. Уравнения эта эквивалентны вышеприведенным уравнениям минимума упругой работы. Уравнения линейны относительно неизвестных, но большое число их и вхождение всех неизвестных  в каждое уравнение чрезвычайно затрудняет их решение. Приведение их к такому виду, при котором в каждом уравнении останется только по одному неизвестному (последовательно: X₁, X₂,…, X_n) называется приведением системы к диагональным членам (α₁₁Х₁, α₂₂Х₂, …, α_nnХ_n) или к нормальным координатам. Задача эта существенно облегчается тем что коэффициенты α, симметричные относительно нисходящей диагонали, равны между собой, т. е. α_kl=α_lk (принцип Максвелла). В настоящее время разработан ряд методов, облегчающих решение этих уравнений (приведение уравнений к «клапейроновскому» виду, т. е. сохранение в каждом лишь трех неизвестных; перенесение неизвестных к особо избираемым осям координат, превращающее в ноль ряд побочных (т. е. не диагональных) коэффициентов; применение метода неопределенных множителей, т. е. метода Гаусса, понижающего постепенно на единицу число уравнений, а соответственно число неизвестных, и т. д.). В результате статическая неопределимость всегда может быть раскрыта.

По определении условий работы каждой части инженерного сооружения остается проверить или окончательно установить размеры данной части, дабы напряжения материала в ней не превосходили известной безопасной доли предела упругости. Чем тщательнее ведется расчет, тем большая доля предела упругости может быть допущена. Современные русские нормы расчета металлических мостов (1921 г.) доводят допускаемые напряжения литого железа в мостах до 16 кг мм² при учете всех условий его работы, что, при пределе упругости мостового металла около 22 кг/мм², дает около 70% от этой последней цифры.

Брусчатые сооружения за последние десятилетия принимают громадные размеры, и ныне мы уже имеем, как рекордные размеры таких сооружений, мосты пролетом в 555 м (мост через реку Delaware в Америке), дома высотой в 200 м (здание Woolworth в Нью-Йорке; см. ниже строительное искусство) и башен высотой в 300 м (Эйфелева башня в Париже).

Некоторые инженерные сооружения не могут быть подведены под схему сооружений брусчатых. Таковы прежде всего сооружения, некоторые элементы которых представляют собой плоские или криво-поверхностные пластинки малой толщины, т. е. тела, в коих измерение, перпендикулярное   поверхности пластинки, ничтожно сравнительно с двумя другими измерениями; прекрасными примерами таких сооружений являются корпус корабля или гондола аэроплана, так как в обоих этих сооружениях наружная стояка и внутренние переборки и перегородки никоим образом не могут быть приведены к брусьям.

Наконец, возможны и сооружения, формы которых представляют собой тела трех измерений; как пример такого сооружения можно привести высокую и широкую, но не длинную плотину из камня или железобетона. Плотина Camarasa, например, возведенная в Испании близ Барселоны, при высоте в 100 м и ширине подошвы в 76 м (сечение  — прямоугольный треугольник, вертикальным катетом обращенный к напорному водному бьефу), имеет полную длину более 250 м, а рабочую длину лишь в 150 м (концы заделаны в скалу). Ясно, что такая дамба не может быть приведена при расчете ее к брусу или к системе брусьев.

Для расчета этих двух категорий сооружений применяются особые методы:

Пластинка изучается в отношении изменений формы ее срединной поверхности — толщинное же ее измерение принимается за величину незначительную, и устанавливается положение, что перпендикуляры к срединной поверхности пластинки остаются перпендикулярными к ней при всех ее деформациях,  и что все точки тела, находившиеся на каком-либо перпендикуляре до действия сил на тело, остаются на том же перпендикуляре и при деформациях пластинки под действием приложенных к ней сил (черт. 10). Это положение аналогично закону сохранения плоских сечений в брусе. В результате задача сводится к изучению работы срединной поверхности пластинки и деформации этой поверхности от действия приложенных сил.

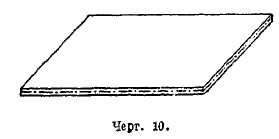
Черт. 10.

В то время как каждый элемент бруса подвергается действию шести сил и пар: N_s, Q_x, Q_y — М_s, М_x, М_у, — каждый элемент пластинки, образованный четырьмя плоскостями, проведенными перпендикулярно к срединной поверхности пластинки, подвергается также действию шести факторов, но уже иных, а именно: N_x, N_y—Q_x, Q_y—М_x, М_y, где ось OZ считается направленной перпендикулярно к поверхности пластинки в данной ее точке (черт. 10). Кручение этого элемента и сжатие его силами, направленными по оси OZ, как правило, игнорируется.

Теория пластинок за последние десятилетия сделала крупные успехи, и все главнейшие случаи исследованы достаточно подробно. Однако, сложность этого вопроса с чисто математической точки зрения оставляет еще в этой области широкое поле для исследований.

Задача в трех измерениях есть, в сущности  задача теории упругости (см. упругость), однако за последние десятилетия практика строительного и машиностроительного дела выдвинула столько проблем в этой области, что и строительная механика частично занимается этим вопросом. Здесь уже речь идет о теле в целом, и заменить его какой-либо эквивалентной схемой нельзя. Однако, и здесь делается некоторое ограничение, а именно, принимается, что вырезанный из тела элемент dx x dy x dz под влиянием действующих на тело сил меняет свое положение относительно неподвижных осей координат, поворачивается относительно этих осей и изменяет свою форму, но сохраняет параллелизм своих граней  и ребер, т. е. превращается в косоугольный параллелепипед, а не в неправильный шестиугольник. На этот элемент уже не могут действовать моменты, и действие на него окружающей среды сводится к шести следующим факторам: ∂N_x, ∂N_y, ∂N_z—∂Q_x, ∂Q_y, ∂Q_s.

Большое значение имеет частный случай трех измерений — плоская задача, которую следует отличать от задачи о пластинке. Плоская задача имеет место тогда, когда тело имеет удлиненную призматическую форму и когда силы действуют на любом поперечном участке тела единообразно. Хорошим примером плоской задачи является выше уже упомянутая задача о плотине, на которую в любом ее сечении действуют однообразные силы в виде гидростатического давления воды, давления грунта и веса самого сооружения. При решении плоской задачи ограничиваются рассмотрением одного какого-либо поперечного сечения данного призматического тела.

В общем и целом основные проблемы строительной механики могут считаться разрешенными; но множество частных случаев еще представляется подлежащим разработке и решению при помощи того могущественного орудия, которым всегда пользуется строительная механика в своих работах, а именно математического анализа.

Библиография. Тимошенко, С. П., «Курс статики сооружений», 1926, Лиг. — Проскуряков, Л. Д., «Строительная механика». — Черепашинский, М. М., «Курс строительной механики». — Прокофьев, И. П., «Теория сооружений», 1926. — Велихов, П. А., «Краткий курс строительной механики», 1927 — Pirlet, «Statik der Baukonstruktiomen», 1920. — Molitor, «Тhe Kinetic Theory of Structures». — Schlink, «Statik der Rautafachwerke». — См. также библиографию при сопротивлении материалов.

П. Велихов.