Свет

Свет. Учение о свете, или оптика, первоначально охватывало собой исключительно те явления, которые производят непосредственное воздействие на орган зрения и вызывают в нас ощущение света. Позднее, когда все более и более стала выясняться физическая основа световых явлений, оказалось, что световые явления составляют частный случай более обширного класса явлений: были открыты так называемые невидимые лучи, подчиняющиеся тем же самым законам, что и видимые, но не действующие непосредственно на глаз. Таким образом, в настоящее время учение о свете стало гораздо шире, оно теперь охватывает некоторые области, которые раньше относились к другим главам физики: так, например, учение о так называемом «лучистом тепле». Отсюда ясно, что печать, наложенная нашими органами чувств на развитие науки, сказывающаяся уже в старинном разделении науки на главы соответственно нашим органам чувств, как, например, звук, свет, тепло, постепенно стушевывается, и это медленное вытеснение «антропоморфного элемента» из современной науки является, как метко указал профессор М. Планк, едва ли не лучшим доказательством ее прогресса.

Излагать учение о световых явлениях почти невозможно, не коснувшись теории света. Едва ли найдется другая область физики, в которой с равным ожесточением велась борьба между различными теоретическими воззрениями: в первой половине XIX в. волнообразная теория окончательно восторжествовала над теорией испускания (эмиссионной) Ньютона, и в свою очередь в конце 80-х и в начале 90-х годов XIX в. она должна была уступить место электромагнитной теории, высказанной впервые в 60-х гг. XIX в. гениальным английским физиком Максвеллом. Наконец, в наши дни появилась новая теория «световых количеств», или «квант», которая, впрочем, как это, по-видимому, выясняется за последнее время, касается лишь способа возникновения или испускания видимых и всевозможных невидимых лучей и не касается вовсе самого механизма распространения света, видимого или невидимого в той или иной среде (см. излучение). На основании сказанного можно подумать, что все учение о свете должно явным образом носить следы потрясений, вызванных сменой руководящих теорий, но более близкое знакомство с современной оптикой вполне устраняет подобные подозрения. Волнообразная теория действительно сильно отличается от эмиссионной: она значительно проще объясняет большие группы явлений, а главное, как мы увидим ниже, основные посылки теории Ньютона опровергнуты строгими опытами. Что же касается перехода от старой волнообразной теории к электромагнитной, то он никакими потрясениями не сопровождался, как не сопровождается потрясениями переход от частного к общему. В современных книгах по электромагнитной теории целые главы переписаны из старых учебников, основанных на старой теории. Таким образом, все старое вошло в состав нового, как  часть. Зато электромагнитная теория дает объяснение уже известным ранее явлениям, которые оставались необъясненными или объяснялись с натяжкой старой волнообразной теорией, а также позволяет предсказывать новые явления, новые факты.

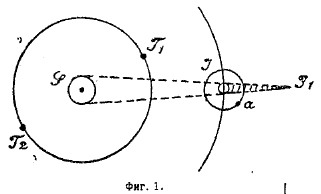
Фиг. 1.

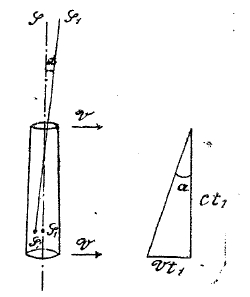
Фиг. 2.

1. Измерения скорости света. Остановимся, прежде всего, на способах измерения скорости света, т. е. скорости, с которой распространяется то, что мы называем светом.

а) Способы астрономические. В 1675 г. датский астроном Олаф Рёмер определил время обращения одного из спутников Юпитера, измерив промежутки времени, отделявшие начала двух последовательных затмений спутника самой планетой (см. фиг. 1: J — Юпитер, J₁ — конус тени его, а — спутник). Этот промежуток оказался равным 42 часам. Рёмер, воспользовавшись этим числом, составил таблицу времени начала затмений на год вперед; при сравнении этой таблицы с наблюдениями, оказалось, что затмения наступают все позже и позже; через полгода разница достигла приблизительно 1 000 секунд, но затем она начала убывать, а через год момент наступления затмения совпал с вычисленным. Рёмер объяснил это явление тем, что при перемещении земли по орбите от T₁ до Т₂ (фиг. 1) расстояние от земли до Юпитера увеличивается на величину, равную диаметру орбиты земли, — около 3 10⁸ км, и свет проходит это расстояние в 1 000 секунд, чем и объясняется запаздывание. Из этих данных получается для скорости света 300 000 км  в секунду.

Другой астрономический способ был предложен Брадлеем в 1727 г. Способ этот основан на измерении угла аберрации (см.), т. е. кажущегося изменения направления, по которому видна звезда. Пока свет, двигаясь по трубе от объектива О (фиг. 2), дойдет до S₁ (промежуток времени t₁), труба, двигаясь с земным шаром со скоростью V, успеет переместиться на некоторое, хотя и малое, расстояние s’₁s, почему изображение звезды S, находящейся вблизи полюса эклиптики (см. эклиптика, аберрация), будет находиться не в S₁ как получилось бы оно, если бы труба была неподвижна, а в S'₁, почему и звезда нам будет казаться находящейся не в S, а несколько смещенной в сторону движения S'. Из прямоугольного треугольника (фиг. 2) имеем:

Vt₁ = ct₁ tgα, или с = v/tgα; откуда, зная скорость земли по орбите и измерив угол аберрации α, найдем скорость света с. (Через полгода скорость земли будет иметь противоположное направление, и та же звезда будет смещена настолько же в противоположную сторону; откуда, разделив пополам полугодовое перемещение звезды, получаем α). Этот способ дал приблизительно ту же величину в 300 000 км в секунду.

в) Первым, измерившим скорость света на земле, был французский физик Физо (1849): он пропустил луч света между зубцами быстро вращающегося зубчатого колеса; далее этот луч, прошедший несколько верст, отражался от зеркала и шел обратно; при известной скорости вращения колеса вернувшийся назад луч уже не попадал в пространство между зубцами, так как за это время колесо успевало повернуться на расстояние, отделяющее средину зубца от средины промежутка, откуда, зная время обращения колеса и расстояние, проходимое светом, нетрудно найти величину скорости света; она получается приблизительно равной 300 000.

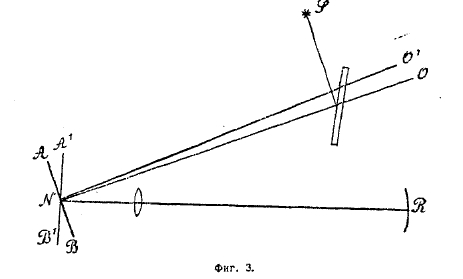
Фиг. 3.

При всем остроумии этот способ неудобен тем, что требует установки двух пунктов наблюдения на расстоянии нескольких верст.

Гораздо интереснее способ Фуко, который не требует для своего осуществления таких больших пространств, как предыдущий. Измерение можно производить в пределах лаборатории. На фиг. 3 изображена схема прибора Фуко. Свет  от источника S, отразившись от пластинки зеркального стекла рр, попадает на вращающееся зеркало А'В' и, отразившись от него и зеркала R, возвращается на вращающееся зеркало, которое за это время уже успело немного повернуться и занять положение АВ, отчего и отраженный от него возвращающийся луч попадет не в О, а в О'; наблюдая это смещение, мы можем определить, на какой угол повернулось зеркало, а зная число оборотов его в минуту, можем определить, сколько потребовалось на это времени; найденный промежуток времени и покажет, сколько надо времени свету, чтобы пройти из N в R и обратно.

Способ Фуко интересен тем, что благодаря небольшим размерам между зеркалами АВ и R можно вносить различные прозрачные среды (стекло, воду и т. д.) и определять в них скорость света. Таким образом, было впервые доказано, что скорость света в воде и в стекле меньше, чем в воздухе; этими опытами и была окончательно опровергнута теория истечения Ньютона, которая объясняла явление преломления тем, что движение света в оптически более плотных средах (стекле, воде) быстрее, чем в воздухе. Впоследствии подобными опытами Майкельсон доказал, что отношение скоростей света в воздухе и в воде равно 1,33, т. е. совпадает с величиной показателя преломления (см. дисперсия света).

2. Прямолинейное распространение света. Одним из наиболее серьезных препятствий, стоявших на пути развития волнообразной теории, было противоречие между всем известным фактом распространения волн вокруг препятствий, стоящих на пути их движения, и не менее известным фактом прямолинейного распространения свет, выражающимся в явлении теней (см. лунное затмение). По теории испускания Ньютона (эмиссионной) лучи представляют собой не что иное, как пути, по которым летят световые частицы. В 1665 г. Гримальди при более тщательном исследовании краев тени (см. ниже) открыл, что свет загибается внутрь конуса полной тени, и что, следовательно, наше представление о прямолинейном распространении света есть только приближение. Рассмотрим, как объясняет волнообразная теория факт прямолинейного распространения. Первый шаг в этом направлении был сделан знаменитым голландским физиком Христианом Гюйгенсом (см.).

Фиг. 4.

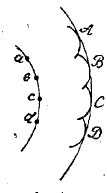
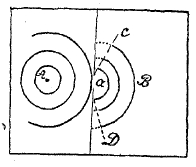
Положим, что в некоторый момент волна, идущая по воде от брошенного в нее камня, разрослась до abсd (фиг. 4); как известно, она будет двигаться и дальше и спустя некоторый промежуток времени достигнет круга ABCD. По Гюйгенсу, волна ABCD образовалась из  волны abсd следующим образом: как   только волна достигла фронта abсd, каждая точка этого фронта становится источником вторичных волн, идущих от abсd и т. д., как это показано на фиг. 4.; при этом точки А нового фронта достигнет прежде всего волна, имеющая центр в ближайшей к ней точке а старого фронта. Таким образом, по Гюйгенсу, каждая точка фронта, занимаемого волной, является источником вторичной волны, а та поверхность, которая касается разом всех вторичных волн (огибающая), представит собой новый фронт распространяющейся волны. Это положение и представляет собой так называемый  «принцип Гюйгенса». В справедливости его можно убедиться на следующем опыте: если мы будем заставлять падать капли на поверхность воды или ртути в точке А сосуда АВ (фиг. 5), то волны будут расходиться в виде кругов; если же на пути этих волн мы поставим перегородку с отверстием а, то по другую сторону перегородки в В мы увидим волны в виде кругов, но с центром в а. Таким образом мы убеждаемся, что малая часть волны а, распространяющаяся из А, сама становится источником волн. Но объясняет ли этот принцип прямолинейное распространение?

Фиг. 5.

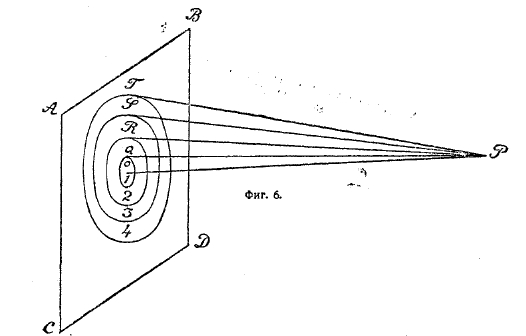
Из фиг. 4 мы видели, что каждая точка нового фронта А получается от волны, идущей из ближайшей точки а старого фронта, но, с другой стороны, если бы мы в а поставили препятствие, то в А все-таки получилось бы движение благодаря тому, что туда пришли бы волны, идущие из b, и т. д.; ведь волны распространяются во все стороны (см. а фиг. 5). Таким образом, объяснение Гюйгенса недостаточно. Следующий шаг был сделан Френелем. Представим себе часть фронта плоской волны ABCD (фиг. 6). В тот момент, когда волна занимает этот фронт, каждая точка этой плоскости становится центром вторичной волны, и движение в Р будет результатом совместного действия всех этих вторичных волн, но различные части плоскости АВ удалены от Р неодинаково, следовательно, вторичные волны придут в Р от разных частей фронта с различным запаздыванием. Опишем из Р, как из центра, сферы радиусами, равными PQ, РК, PS и т. д., отличающимися друг от друга на величину λ/2 (половину длины волны), т. е. половину расстояния от гребня одной волны до гребня следующей; эти сферы пересекут плоскость ABCD по кругам и разделят всю плоскость на пояса или зоны 1, 2, 3, 4 и т. д. Если мы рассмотрим действия двух последовательных поясов, то заметим, что любой вторичной волне, идущей от одного пояса, можно найти соответствующую, идущую от соседнего, запаздывающую на λ/2, т. е. одновременно с гребнем одной придет долина другой. Таким образом, действия двух последовательных поясов противоположны, и они почти взаимно уничтожают друг друга — почти, потому что площади поясов по мере удаления от центра возрастают, так что число точек, посылающих волны в более отдаленных поясах больше. Это неравенство однако уравновешивается, и уравновешивается тем более, чем дальше мы отходим от центра О, т. е. чем более высокого порядка пояса мы рассматриваем, в силу двух причин: во-первых, расстояние увеличивается, а чем дальше отошла волна от ее центра, тем меньше становится амплитуда (высота гребня или глубина долины волны). Следовательно, действие слабеет с расстоянием; во-вторых, волна, идущая от очень удаленного пояса, сильно наклонена к фронту ABCD, а из опыта известно, что амплитуда значительно больше по направлению В (фиг. 5), чем по направлению С и D, сильно наклоненными к фронту подошедшей из А в а волны. Таким образом отдаленные пояса волн ABCD (фиг. 6) взаимно уничтожаются, и в Р действуют только самые близкие к О пояса. Обсуждая действие ближайших поясов, можно теоретически показать, что оно сводится приблизительно к действию половины первого пояса. В самом деле, обозначая амплитуду движения, производимого первым поясом, через y, вторым — y₂ и т. д., мы получим для общего действия

У = у₁—у₂+y₃—у₄.. .(1), так как действия последовательных поясов противоположны. Ряд (1) можно написать

У = y₁ — (у₂ — у₃) — (у₄ — у₅)—… (1); так как  действие каждого следующего пояса слабее предыдущего, то все разности у₂ — y₃ и т. д. положительны и, так   как они  все вычитаются из у₁ то ясно, что У < y₁ т. е. общее действие меньше действия первого пояса. С другой стороны ряд (1) можно написать так:

У = y₁/2 + (y₁/2 – y₂ + y₃/2) + (y₃/2 – y₄ + y₅/2) + … (3), откуда

У > y₁/2, т. е. действие больше, чем действие ½  первого пояса.

Итак, для точки Р в волне ABCD «деятельной» является только часть, непосредственно примыкающая к О (перпендикуляру, опущенному из Р на плоскость волны, или «лучу»); теперь ясно, что если длина волны λ будет очень мала, то и все «деятельные» пояса займут очень небольшую область вокруг О, и всякое малое препятствие, поставленное в О, достаточное однако, чтобы закрыть все «деятельные» пояса, не пропустит волны в Р. Волны света в среднем имеют длину около 0,00005 сантиметра (см. ниже). Таким образом, все деятельные пояса волны ABCD займут ничтожную область с радиусом в очень малую долю миллиметра. Таким образом, кажущаяся прямолинейность распространения света объясняется тем, что световые волны малы по сравнению с теми препятствиями, какие мы ставим на их пути. Поставив на пути ряби, бегущей по поверхности пруда, доску, мы займем большую часть деятельных поясов, и за доской будет затишье — «тень». Но та же доска, как бы мы прочно ее ни закрепляли, не даст тени от океанской волны!

Выделяя на последовательных фронтах волны деятельные ее части, мы получим «луч», т. е. ограниченный пучок света, распространяющийся независимо от того, что происходит в соседних с этим пучком областях.

3. Отражение и преломление. Законы отражения и преломления можно рассматривать, исследуя ход лучей, как это обыкновенно делается в так называемой «геометрической оптике», рассматривающей действие оптических инструментов, зеркал, стекол и т. д., или исследуя, как изменяется при отражении и преломлении фронт волны. Этот второй путь, например, последовательно проведен в учебнике А. Г. Столетова «Акустика и Оптика» (1892).

Фиг. 6.

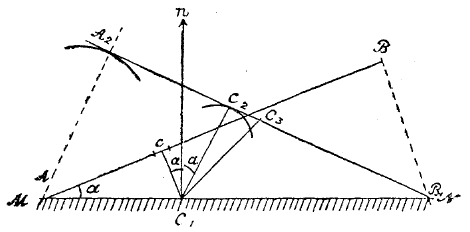
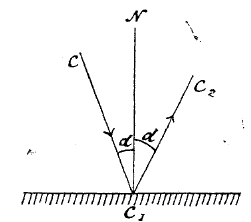
Положим, плоская волна АВ (фиг. 7) падает на плоское зеркало MN. Любая точка А, находящаяся на зеркале, став в известный момент центром волны, может посылать волны только в одну сторону (на фиг. 7 вверх от MN). Когда падающая волна АВ коснется зеркала в В₁, вторичная волна из точки А успеет распространиться до сферы радиуса АА₂ = ВВ₁ проводя из B₁ касательную к А₂, мы получаем фронт волны отраженной B₁A₂; из прямоугольных треугольников AA₂B₁ и АВВ₁, имеющих равные катеты АА₂ и BB₁ и общую гипотенузу АВ₁, находим, что углы падения и отражения α при А и В₁ равны между собой (основной закон отражения). Обыкновенно за угол падения и отражения принимают углы, образованные не самим зеркалом с фронтами волны, а углы между перпендикулярами к плоскостям волн и зеркалу ∟CC₁n = ∟ nС₁С₂, иначе углы между «лучом» падающим и отраженным и нормалью к зеркалу (фиг. 8). Нетрудно показать, что части С₂ (фиг. 7) отраженной волны С на падающей.

Фиг. 7.

В самом деле, когда область С падающей волны коснется С₁, — С₁ станет центром волны (вторичной), которая к моменту, когда отраженная волна займет положение А₂В₁, коснется А₂В₁ в точке С₂.

Если мы докажем, что СС₁+С₁С₂=АА₂ для любой точки С, т. е. что путь, пройденный всеми частями волны, одинаков, то действительно А₂В₁ будет огибающей всех вторичных волн. Из прямоугольных подобных треугольников Δ АВВ₁ ~ Δ АСС₁ имеем СС₁/ВВ₁ =  АС₁/АВ₁… (2); точно так же из треугольников Δ АА₂В₁ ~ Δ В₁С₂С₁ имеем С₁С₂/АА₂ = С₁В₁/АВ₁…(3); заменяя в (2) ВВ₁ = АА₂ и складывая (2) и (3), находим: (СС₁+С₁С₂)/АА₂ = АВ₁/АВ₁ = 1, т. е. СС₁ + С₁С₂ = АВ₁, что и требовалось доказать. Путь от С к С₂ через С, представляется кратчайшим от точки С до фронта А₂В₁ с условием, что на этом пути надо зайти на зеркало; в самом деле, если мы соединим  С с другой точкой С₃, то путь будет длиннее: перпендикуляр С₁С₂ короче наклонной С₁С₃. Поэтому закон отражения формулируется часто, как принцип «кратчайшего пути» (принцип Ферма).

Фиг. 8.

Фиг. 9.

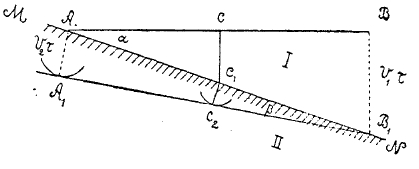
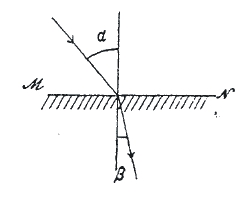
При переходе из одной прозрачной среды в другую наблюдается явление преломления света. Положим, что граница, отделяющая I прозрачную среду от II, представляет собой плоскость МN (фиг. 9); пусть на нее падает плоская волна АВ, и пусть волна движется в первой среде со скоростью V₁ и со скоростью V₂ во второй. По истечении некоторого времени τ часть фронта падающей волны достигнет В₁, пройдя расстояние ВВ₁ = V₁τ. К тому времени точка В₁ станет центром вторичной волны, но за тот же промежуток времени τ вторичная волна, выйдя из А во второй среде, пройдет путь AA₁ = V₂τ, меньший, чем путь ВВ₁ = V₁τ,   если V₂ < V₁, т. е. если скорость распространения волны во второй среде меньше, чем в первой; из двух прямоугольных треугольников АВВ₁ и А₁АВ₁ имеем ВВ₁ = V₂τ = АВ₁ sin α (1) и АА₁ = V₂τ =AB₁ sin β (2); деля почленно (1) на (2), имеем sin α/ sin β = V₁/V₂ = n₁₂ (3) – основной закон преломления. Можно, так же, как и для отражения, показать, что А₁В₁ является огибающей всех вторичных волн С₁С₂; при этом ход луча СС₁С₂ представляется таким движением, при котором можно из данной точки С прийти на фронт волны В₁А₁ в кратчайший срок: «принцип быстрейшего прихода» (Ферма). Рассматривая ход лучей, направление которых совпадает с перпендикуляром к волне, мы придем к построению фиг. 9а.

Фиг. 9а.

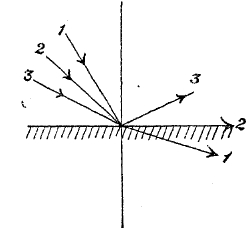
Итак, основной закон преломления может быть формулирован так: отношение синусов углов падения и преломления есть величина постоянная, причем эта постоянная, называемая относительным показателем преломления n₁₂ равняется отношению V₁/V₂ скоростей света в первой и во второй среде. На фиг. 9b изображен ход лучей при переходе из среды, в которой свет двигается медленнее, в среду, где он движется быстрее (V₁ < V₂). В этом случае угол преломления больше угла падения; при некотором угле, называемом предельным, зависящим от показателя преломления, угол преломления достигает 90°, т. е. преломленный луч стелется вдоль поверхности раздела (см. 9b, 2). Так как sin 90 = 1, то предельный угол определяется условием sin α = n₁₂ = V₁/V₂. Если угол будет больше предельного, то преломленного луча не получится; падающий луч отражается от поверхности раздела — явление полного внутреннего отражения. Показатель преломления может быть измерен, если мы на опыте определим углы α и β и вставим эти величины в (3). Одним из очень важных подтверждений волнообразной теории является совпадение найденной таким образом величины с указанным выше непосредственным измерением скоростей света. V₁ и V₂ в различных средах, а следовательно, с непосредственным измерением величины V₁/V₂.

Фиг. 9b

На этих двух законах отражения и преломления основывается вся так называемая геометрическая оптика. Первоначально геометрическая оптика развивалась без каких бы то ни было представлений о волнах; луч рассматривался как нечто абсолютное, и это не мешало построить весьма стройную теорию оптических инструментов. Однако волнообразная теория, показывающая, что представление о луче возникло у нас только благодаря тому, что волны света очень малы сравнительно с препятствиями, какие мы ставим на их пути, и что прямолинейное распространение света есть только некоторое приближение, а не что-нибудь абсолютное, позволило значительно расширить учение геометрической оптики, указать новые пути для усовершенствования оптических приборов и вместе с тем указать пределы, дальше которых мы не можем идти в увеличении микроскопа и телескопа; пределы эти обусловлены самой волнообразной природой света. Рассмотрим вкратце элементарную теорию оптических инструментов.

Фиг. 10.

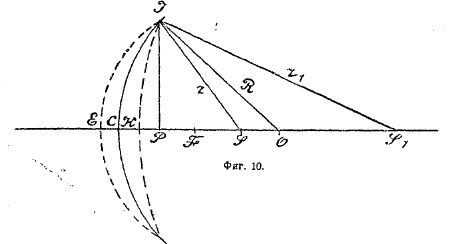
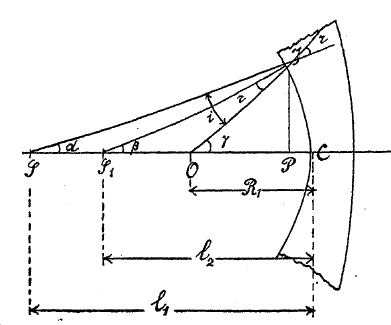
4. Оптические инструменты. а) Вогнутое зеркало. Представим себе, что на вогнутое зеркало радиуса R (фиг. 10) падает волна, выходящая из точки S, лежащей на прямой (главной оптической оси), соединяющей вершину зеркала свет с центром О. Если бы зеркала не было, то в некоторый момент волна, выйдя из S, распространилась бы до ІЕ. Но так как зеркало не пускает волну дальше IС, волна отражается, и в рассматриваемый момент отраженная волна успеет пройти назад такой же путь СН, какой она прошла бы вперед ЕС, если бы зеркала не было. Итак, ЕС = СН; если мы сделаем то же построение для всех частей зеркала, то получим для отраженной волны фронт ІН, представляющий собой приблизительно поверхность сферы с радиусом IS₁ = r₁,   так что отраженная волна соберется приблизительно в одной точке S₁, называемой изображением точки S, т. е. источника наших волн. Основной задачей является уменье по величине радиуса зеркала R и расстоянию источника S от вершины зеркала С—SC = d определить расстояние изображения CS₁ = d₁. Эта задача решается простым геометрическим построением (фиг. 10 и 11).

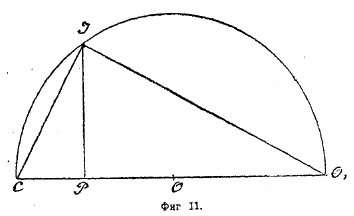
Фиг. 11.

Построив на диаметре зеркала СО₁ окружность CIO₁ и соединив точки I с С и О₁, мы получаем прямоугольный треугольник CIO₁ (угол при I опирается на диаметр и, следовательно, — прямой), IP высота треугольника. Из свойства прямоугольного треугольника: высота, опущенная из вершины прямого угла на гипотенузу, есть средняя пропорциональная между отрезками гипотенузы, — имеем IP² = СР.(2R — СР), и так как во всех встречающихся на практике случаях сферическое зеркало составляет очень малую часть сферы R, то СР величина малая, а потому мы можем заменить приведенное соотношение упрощенным: IP² = CP.2R или СР = IP²/2R…(I). Проделав то же  построение для r₁ и r (фиг. 10), найдем СР = IP²/2r…(II) и НР = IP²/2r₁…(III). Так как мы видели, что ЕС = СН, а, с другой стороны, ЕС = ЕР – СР и СН = СР – СН, то ЕР – СР = СР – СН (IV); вставляя (IV) (I) (II) (III) и сокращая на IP², получаем:

1/2r + 1/2R =  1/2R – 1/2r₁, или 1/2r + 1/2r₁ = 1/R₁, или 1/r + 1/r₁ = 2/R; так как все величины ЕР, ЕС и ЕН малы, то вместо r и r₁ можно поставить расстояния S и S₁ от вершины С, т. е. величины d и d₁, откуда

1/d + 1/d₁ = 1/(R/2) = 1/F… (A)

Формула (А) есть основная формула для сферического зеркала, и, так как мы увидим, что к выражению (А) может быть приведена и основная формула преломления света в оптических стеклах, то (А) является основной формулой для приблизительного расчета всех вообще оптических инструментов; величина F = R/2 называется главным фокусным расстоянием. Разберем ф-у (А); 1) случай: S лежит между F и O, скажем, например, посредине, тогда d = ¾ R и 1/d₁ = 2/R – 4/3R = 2/3 1/R или d₁ = 3R/2: если предмет находится между центром и фокусом, то изображение лежит за центром; так как наша ф—а (А) симметрична относительно d и d₁ то и обратно — если d = 3R/2, то d₁ = ¾ R, т. е. если предмет лежит за центром по отношению к зеркалу, то изображение находится между фокусом и центром. 2) Предмет находится в центре, d = R, ф-а дает d₁ = R, т. е. предмет и его изображение совпадают. 3) Предмет лежит в фокусе, d = R/2, ф—а (А) дает 1/d₁ = O, т. е. d₁ должно быть бесконечно велико, точно так же, если предмет лежит очень (бесконечно) далеко, 1/d = 0 и 1/d₁ = 2/R, т. е., d₁ = R/2.

Итак, бесконечно удаленный предмет дает изображение в славном фокусе, и наоборот, предмет, находящийся в главном фокусе, дает изображение в бесконечности, т. е. получается плоская волна, а плоскость можно рассматривать как часть сферы бесконечно большого радиуса. Иначе предмет, помещенный в фокусе (маленькое светящееся тело), дает «пучок параллельных лучей».

Фиг. 12.

4) d<R/2, скажем d = R/4,   тогда 1/d = 2/R – 4/R = -2/R, d₁ = -R/2; знак – показывает, что изображение лежит за зеркалом, т. е. изображения не получается, отраженная волна получается расходящаяся, притом так, как будто центр ее находится за зеркалом; при рассматривании предмета, поставленного таким образом перед зеркалом, нам будет казаться, что его изображение находится за зеркалом, такое изображение называется мнимым, мы его можем наблюдать глазами, но не можем принять на экран, например, на кусок белой бумаги, так как в действительности лучи не пересекаются; мы видим изображение там, где пересекаются продолжения расходящихся лучей.

То же построение, какое мы получили с волнами, можно, как это и было указано выше, получить и с лучами, пользуясь основным законом отражения (см. выше).

в) Сферическое стекло, или линза. Сферическим стеклом, линзой (чечевицей) называется шлифованное стекло, ограниченное двумя сферическими поверхностями; линия, проходящая через центры этих поверхностей и через центр линзы, называется главной оптической осью.

Исследовать действие можно было бы так же, как мы исследовали действие вогнутого зеркала, т. е. исследовать, как изменяется кривизна волны при прохождении через преломляющиеся поверхности; но, чтобы показать, как располагаются построения при помощи лучей, рассмотрим вкратце теорию линзы, исследуя ход «лучей».

Пусть источник света (светящаяся точка) находится на главной оптической оси в S (фиг. 12). Рассмотрим луч SI, проведем из О — центра первой поверхности ІС радиус и построим преломленный луч; нормалью (перпендикуляром) к поверхности в данном случае будет радиус OI; продолжаем преломленный луч до пересечения S₁ с главной оптической осью; из треугольников SIO и S₁lO имеем α + I = γ и β + r = γ(1).

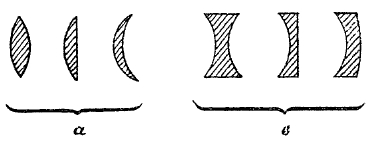
Фиг. 13.

Если рассматривать лучи, идущие под малым углом к оптической оси, то углы i и r будут малые, и, следовательно, можно вместо формулы sin i = n₁₂sin r воспользоваться приближенной I = n₁₂r; умножив второе из выражений (1) на n₁₂ и вычитая из него первое, получим n₁₂β — α = γ (n₁₂ — 1).... (2); кроме того, так как α, β и γ малы, α = IP/SP, β = IP/S₁P  и γ = IP/OP; вставив эти выражения в (2) и сокращая по IР имеем n₁₂/S₁P – 1/SP = (n₁₂ – 1)(1/OP) (3) и, наконец, заменяя SP, S₁P и ОР близкими к ним величинами I₁ I₂ R₁ (фиг. 12) — близкими потому, что при данных условиях (малости углов α, β и γ) отрезок PC мал, получаем n₁₂/I₂ – 1/I₁ = (n₁₂ – 1)1/R₁.... (4), точно так же для второй поверхности получим  n₁₂/I₄ – 1/I₃ = (n₁₂ – 1)1/R₂.... (5), для этой поверхности источником будет служить S₁. Если мы будем полагать, что стекло тонкое, то I₂ = I₃, т. е. расстояние от S₁ как от первой, так и от второй поверхности, одно и то же; подставляя I₂ = I₃ и замечая, что n₁₂ = 1/n₂₁, так как n₁₂ = V₁/V₂, а n₂₁ = V₂/V₁, находим 1/l₄ – n₁₂/I₂ = -(n₁₂ – 1)1/R₂ (5’); складывая (4) и (5’), найдем 1/I₄ – 1/I₁ = (n₁₂ – 1)(1/R – 1/R₂)…(6).

Обыкновенно принято считать расстояния l₁ и I₂ положительными, когда они лежат по обе стороны линзы, а не так, как в нашем примере, точно так же радиусы кривизны считаются положительными для выпуклых поверхностей и отрицательными для вогнутых. Итак, полагая I₄ = — d₂, l₁ = d₁ и заменяя знак + на — у R₁, находим

1/d₁ + 1/d₂ = (n₁₂ – 1)(1/R₁ + 1/R₂) = 1/F…(7)

т. е. выражение формально одинаковое с формулой вогнутого зеркала с той только разницей, что фокусное расстояние F выражается теперь через n₁₂, R₁ и R₂, а не через один радиус — как это было для вогнутого зеркала. Пользуясь этой формулой и помня правило знаков для величин R₁ и R₂, можно разобрать действие сферического стекла любого типа (фиг. 13), собирательных (а) и рассеивающих (в). Для собирательных линз 1/R₁ + 1/R₂ > 0, для рассеивающих 1/R₁ + 1/R₂ < 0. На фиг. 14 указано построение  изображений в собирательной и рассеивающей линзе, оно основано на следующем правиле: луч, проходящий через оптический центр, идет без преломления, а луч, параллельный главной оптической оси, проходить чрез фокус для собирательных линз, а для рассеивающих — продолжение преломленного проходит через фокус. Рассмотренная приближенная теория приложима для тонких линз; при расчетах оптических стекол необходимо считаться с влиянием толщины стекол; вообще более строгая теория, знание которой необходимо для конструктора, значительно сложнее.

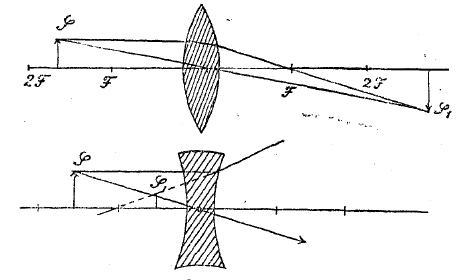
Фиг. 14.

Оптические стекла и зеркала обладают целым рядом недостатков.

а. Сферическая аберрация. Лучи, выходящие из одной точки, не собираются, строго говоря, в одну точку, как мы предполагали, и этот недостаток тем сильнее, чем меньше радиус кривизны, и он уменьшается по мере уменьшения угла в конусе падающих лучей. Устранить этот недостаток — неясность изображения — можно с помощью экрана с небольшим отверстием (диафрагма): при этом устраняются крайние лучи, падающие под большим углом. А лучше всего недостаток этот устраняется комбинацией двух линз, причем одновременно устраняется и хроматическая аберрация. Если сферическая аберрация устранена не только для точек, лежащих на оптической оси, но и для целых площадок, перпендикулярных к оси, то такая комбинация линз называется апланатической.

b. Хроматическая аберрация (см. ахроматизм).

Фокусы 1/F = (n₁₂ – 1)(1/R₁ + 1/R₂) различны для лучей различной преломляемости (цветности) вследствие различия показателя преломления для различной цветности (см. дисперсия).

с. Астигматизм — лучи, выходящие из точки, лежащей на побочной оптической оси, не дают сферической волны и образуют волну, не симметричную относительно этой оси; комбинации линз, свободные от этого недостатка, называются анастигматы.

Фиг. 15.

d. Искривления. 1) Плоский предмет дает изображение, лежащее на вогнутой поверхности, так как фокусное расстояние для побочных лучей несколько иное, чем для центральных; кроме того, получаются 2) искривления, обусловленные различным увеличением для точек близких и далеких от оси; эти недостатки устраняются надлежащим выбором линз и надлежащим положением и размерами диафрагмы.

О преломлении в призме (см. дисперсия и спектроскоп). Все вообще оптические инструменты получаются комбинациями простых и сложных линз (см. астрономическая труба, лупа, микроскоп) и могут быть разобраны на основании изложенной приближенной теории. Двойное преломление см. поляризация.

5. Интерференция света. При объяснении прямолинейного распространения света с точки зрения волнообразной теории, мы уже пользовались представлением об интерференции; мы уже указывали, что свет от двух одинаковых вторичных источников света может производить в данном месте различные действия в зависимости от расстояний, отделяющих место наблюдения от этих источников; если разность расстояний такова, что свет от одного источника придет в данное место наблюдения, опоздав на целое число волн, то мы будем получать гребень волны одного источника вместе с гребнем волны другого; если же опоздание окажется равным нечетному числу полуволн, то гребень будет совпадать с долиной и наоборот; оба источника, следовательно, в данном месте погасят друг друга — мы будем наблюдать темноту. В этом и состоит явление интерференции. Рассмотрим, как оно наблюдается, и как воспользовались этим явлением для дальнейшего изучения природы света.

Фиг. 16.

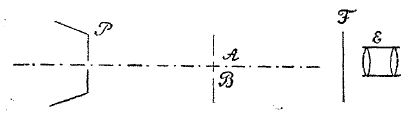
Наблюдать явление интерференции всего проще с помощью расположения Томаса Юнга (фиг. 15). В непрозрачном экране, лучше всего в металлическом листе, делается при помощи иглы отверстие, которое освещается (слева на фиг. 15) ярким источником света, причем необходимо, чтобы свет не проникал иначе, как через отверстие; на расстоянии приблизительно в 30 см устанавливается второй экран с двумя отверстиями (проколами иглы), отстоящими на расстоянии менее полумиллиметра друг от друга (А, В); на расстоянии 30 см от второго экрана помещается лист белой бумаги, а еще лучше, - окуляр от какого-либо оптического инструмента; тогда на экране или в поле зрения окуляра получаются полосы темные и светлые, если освещение было одноцветное, и цветные, если свет был белый, т. о. состоящий из смеси всех цветов спектра (см. спектральный анализ).

Фиг. 17.

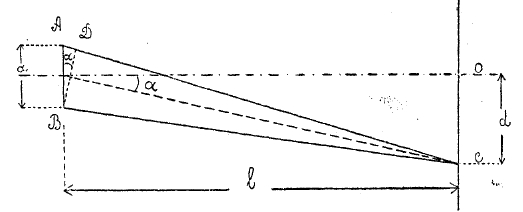
Расположение темных и светлых полос определяется следующим образом; если А и В (фиг. 16) будут два отверстия, играющие роль двух источников света, то на экране в точке О, отстоящей на одинаковом расстоянии от А и В, будет усиление света.

Для любой же точки света будет усиление или ослабление, смотря по тому, на сколько запоздает свет от более удаленного от света источника, т. е. сколько световых волн или их частей уложатся на отрезке АD. Из чертежа следует (принимая малую дугу BD за прямую), что AD = asin α (1) и sin α ~ α = d/I (2), откуда AD = a/I d. Если AD = целому числу волн, то в С будет усиление — светлая полоса; если AD = (2n +1) λ/2 (n-целое число), т, е. нечетному числу полуволн, то в свете всегда будет встречаться гребень волны одного источника с долиной другого. Итак, положение светлых полос определяется условием AD = kλ = a/I d… (3),  где k целое число, а d расстояние полосы относительно центра картины, т. е. о фиг. 16. Темные полосы определяются условием

(2k + 1) λ/2 = a/L d.

Фиг. 18.

Для удачи опыта необходимо, чтобы оба отверстия А и В освещались одним источником, так как мы предполагаем, что из А и В одновременно выходит гребень или долина, что при хаотичности движений центров колебаний в светящихся телах не может произойти, если А и В освещены различными источниками света. В опыте Юнга два отверстия освещены светом, идущим от одного отверстия, следовательно, первоначальный источник один.

Фиг. 19.

Вместо окуляра можно поставить фотографическую пластинку, и тогда можно показать объективно явление интерференции. Образчики подобных снимков можно видеть на таб. 1. Снимки (а также снимки табл. II, см. ниже) сделаны по мысли В. К. Аркадьева в городском университете Шанявского слушателями А. Беркманом и Н. Яковлевым.

На снимках 14а, 14b и 14с освещение производилось попеременно отверстием А, потом В; результат представляет собой то, что происходит при освещении двумя различными источниками, на фиг. 15а, b и с оба отверстия были открыты разом (освещались одним общим источником, как на фиг. 15), на 15b и 15с ясно видны полосы темноты. Приводим числовые данные: диаметр отверстий 0,094 миллиметра расстояния между центрами отверстий в снимках, а 19,5 м/м  в b—4 м/м  и в с 1,2 м/м  расстояние между экраном с одним отверстием и экраном, с двумя отверстиями 16 метров, между экраном с двумя отверстиями и фотографической пластинкой 12 метров. Выдержка на пластинках средней чувствительности 5 минут, освещение первого отверстия — вольтова дуга.

Для получения более яркой картины пользуются зеркалами Френеля; получают два изображения одного и того же источника с помощью двух зеркал или, наконец, би-призмой Френеля: два изображения получаются при пропускании света через пару призм.

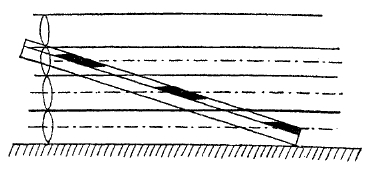
Явления интерференции наблюдаются при встрече волн падающих и отраженных (см. волны и звук); всего проще это явление наблюдается на  веревке, резиновой трубке или свернутой в спираль проволоке, если закрепить один конец и раскачивать ритмически другой. При этом получаются узлы — неподвижные места и пучности в промежутках, где движение наиболее сильно. Винер получал стоячие волны света, заставляя пучок параллельных лучей отражаться от зеркала. Если вблизи зеркала под углом поставить фотографическую пластинку (фиг. 17), то в некоторых местах чувствительный слой попадет в узел, в других — в пучность (чувствительный слой у Винера был очень тонок), в пучностях пластинка чернеет, в узлах остается неизмененной. В опыте Винера по расстоянию между черными полосами можно судить о расстоянии между узлами и, следовательно, о длине волны и показать, что красный цвет соответствует более длинным волнам, а фиолетовый — наиболее коротким из волн видимого света.

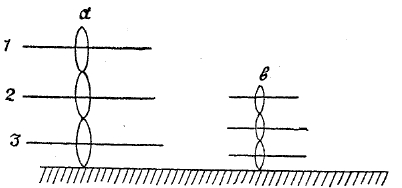
В опыте Винера кроется объяснение цветной фотографии по способу Лимпана. Если взять прозрачную чувствительную пластинку, прилегающую чувствительной стороной к ртути, и поставить в фотографическую камеру, то при съемке в толще чувствительного слоя получаются пленки на расстояниях, соответствующих длинам волн данного цвета. Если проявленную пластинку рассматривать в отраженном свете, то в части а (фиг. 18) отразятся те волны, у которых длина волны в два раза больше  расстояния между слоями; луч, отразившийся от 2, пройдет на одну длину волны λ больше, чем отразившийся от 1 (на двойное расстояние между 1 и 2), точно так же, как в b будет отражен по преимуществу свет с волной более короткой; ясно, что это условие не будет соблюдено в а для волн другой длины, и лучи, идущие от слоев 1, 2, 3, не будут усиливать друг друга, почему из белого света при отражении от а получится свет той волны, которая вызвала появление отражающих слоев. Подобным образом объясняются цвета тонких пластинок, там только речь идет об отражении от передней и задней поверхности фиг. 19, например, в явлении так называемых Ньютоновых колец, получающихся при наложении линзы на плоское стекло, в промежутке между которыми остается слой воздуха, представляющий тонкую пластинку, толщина которой возрастает от центра (место соприкосновения линзы со стеклом) во все стороны одинаково (при условии верности шлифовки линзы и плоского стекла). Так как при значительной по сравнению с длинами световых волн толщине пластинки условия максимального отражения могут совпадать для нескольких спектральных цветов (см. спектр), то цвета тонких пластинок будут цветами смешанными. Явлениями интерференции в настоящее время пользуются при исследовании спектров.

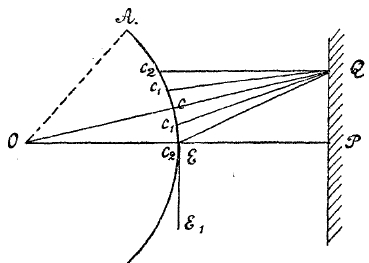
Рис. 20.

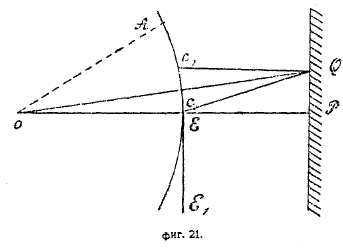
Рис. 21.

6. Дифракция. Дифракцией света называется отступление от прямолинейного распространения света, или явление, состоящее в загибании света внутрь области тени; явление это впервые наблюдал Grimaldi в 1665 г. Обыкновенно к явлению дифракции примешивается явление интерференции. Правильное объяснение этого сложного явления было дано Френелем. Представим себе пучок света, идущий из узкой щели в О (фиг. 20) и падающий на экран PQ; на пути света находится непрозрачный экран ЕЕ₁. Если бы свет распространялся в точности по прямым линиям, то в Р прошла бы граница тени. Применим для данного случая то же построение, каким мы пользовались для объяснения прямолинейности распространения света с точки зрения теории волн. Разобьем фронт волны, касающейся в Е края непрозрачного экрана, на пояса Гюйгенса, соответствующие точке Q, т. е. опишем из Q сферы с радиусами QC₁, QC₂ и т. д., отличающимися на ½ λ — половину длины волны. Все части поясов, лежащие от С к А и дальше, окажут свое действие так, как будто экрана не было, но к этому еще присоединится действие частей двух первых поясов, лежащих между С и Е; действие CC₁ противоположно действию С₂С₁, потому в сумме освещения в Q = половине полного.

Фиг. 22.

Для другой точки Q₁ экрана (фиг. 21), лежащей ближе к Р, между полюсом волны С и краем экрана помещается только один пояс Гюйгенса СС₁, эта часть действует полностью, она не ослабляется действием соседних поясов, освещение, даваемое ею, больше, чем освещения всех частей поясов, лежащих от С к А и дальше. Следовательно, точка Q₁ будет освещена, ярче, чем если бы экрана ЕЕ₁ не было; так как длина волн, определяющая пояса Гюйгенса, зависит от цвета, то места максимального освещения Q₁ фиг. 21 и наименьшего Q фиг. 20 будут различны для различного цвета, отчего при освещении края экрана белым светом мы получим явление окрашенных полос.

На таб. I фиг. 16а—16d приведены снимки дифракционных явлений, происходящих на краю экрана; на 16а экраном служил край бритвы, на 16d свет шел по касательной к цилиндру, сделанному из согнутого картона с радиусом в 40 метров; такая кривизна не играет роли (цифры R обозначают радиусы кривизны), как это видно из снимков. Кривая, расположенная под снимками, изображает теоретическое вычисленное изменение яркости света вблизи края экрана. Эти же снимки показывают в согласии с теоретической кривой, что яркость непрерывно убывает внутрь тени, никаких полос не получается. Но если наш экран ограничен и с другой стороны, если на пути  света мы помещаем маленькую полоску, то и внутри тени,   как показывает рассуждение, подобное приведенному выше, будут полосы. На таб. II показаны снимки, получающиеся при прохождении света сквозь отверстия или мимо небольших дисков. На таб. II ясно видны полосы внутри области тени и яркое пятнышко посредине ее; цифры n дают числа поясов Гюйгенса, занятых экраном или  отверстием. Кольца, подобные изображенным на таблице, получаются при прохождении света мимо ряда одинаковых препятствий, например, круги вокруг солнца и луны, наблюдаемые в те дни, когда в атмосфере взвешены кристаллики льда. Подобные круги существуют во всяком изображении, даваемом микроскопом или вообще каким-либо оптическим инструментом, и налагают предел на увеличение этих инструментов; если изображения колец, соответствующих двум близким точкам изображения, налегают друг на друга, то мы уже не можем различать эти точки, как раздельные. На принципе дифракции основан очень важный инструмент, так называемая дифракционная решетка — важный потому, что он дает возможность измерять длину световых, волн с большой точностью.

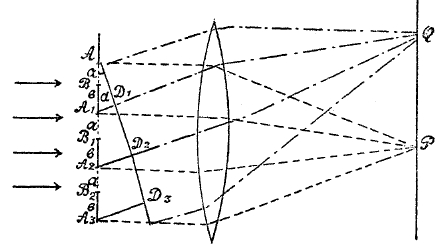
Представим себе решетку, состоящую из ряда непрозрачных полосок BA₁, B₁A₂ и т. д., чередующихся с прозрачными промежутками (фиг. 22), освещенную (слева) пучком параллельных лучей. Пусть за решеткой находится линза L. Из чертежа видно, что в Р все лучи, идущие от решетки, пройдут одинаковые пути, гребни и долины будут приходить согласно, для точки же Q лучи будут запаздывать на величины А₁D₁, А₂D₂ и т. д., они будут усиливать друг друга или ослаблять, смотря по тому, уложится ли на А₁D₁ и т. д. целое число волн или нечетное число полуволн. Таким образом, если для QA₁D₁ = (а + b) sin α = nλ. (1), где n любое целое число, а λ длина волны, то в Q будет максимум света; если же

А₁D₁ = (а + b) sin α = (2n + 1)/2 λ (2) (n любое целое число), то будет minimum. В поле зрения линзы получается ряд полос темных и светлых, если свет монохроматический одноцветный, тогда, измеряя углы α и «период» решетки, т. е. a + b, ширину полосы  + промежуток, по формуле (1), можно определить длину волны λ — это самый лучший способ определения длины волн. Если свет белый, то темные и светлые полосы получаются в разных местах поля зрения для разных цветов, в зависимости от величины λ получаются так называемые дифракционные или «нормальные» спектры. Цвета располагаются в следующем порядке, если считать от центра картины Р в обе стороны: фиолетовый, синий, голубой, зеленый, желтый, оранжевый и красный; дальнейшие спектры от Р после второго отчасти налегают друг на друга, если решетка частая. На современных решетках число полосок на дюйме доходит до 40 000! Чем больше полосок на единице длины, тем менее а+b и тем больше отличаются друг от друга последовательные значения sin α = nλ/(a+b) при n = 1, n = 2 и т. д., т. е. тем реже спектры и тем дисперсия больше; при большой величине 1/(a+b) малые различия в λ при одном и том же n дают большие различия в sin α и α, т. е. отдельные цвета сильнее разделяются.

7) Определение силы света см. фотометр.

8) Поляризация света, поляризатор, анализатор, см. поляризация.

9) Принцип Допплера, см. Допплера явление.

10) Давление света, см. световое давление.

11) Поглощение света, см. спектр, теплота, цвета.

12) Электромагнитная природа света. Рассмотренные в 1, 2, 3, 4 явления могут быть объяснены одинаково как с точки зрения прежней Френелевой волнообразной теории, так и с точки зрения новой волнообразной электромагнитной, так как для объяснения необходим был только самый волнообразный характер движения, природа же его совершенно не играла роли.

14) Впервые электромагнитная природа света была выяснена теоретически Максвеллом. Он указал, что из законов электромагнетизма и электромагнитной индукции в соединении с гипотезой диэлектрического тока или тока смещения в непроводниках (см. электрические колебания; эта гипотеза была впоследствии непосредственно проверена опытами А. А. Эйхенвальда в Москве) следует, что всякое электрическое возмущение распространяется со скоростью V, равной отношению единиц по электростатической системе единиц и электромагнитной (см. электрические измерения и единицы). Отношение этих единиц V равно некоторой скорости, и с этой скоростью, как оказывается, передается по Максвеллу всякое электромагнитное возмущение. Точные измерения отношения V показали, что V = 300 000 км в секунду, т. е. скорости света! Отсюда Максвелл  вывел заключение, что и свет должен быть электромагнитным явлением. С этого времени и вплоть до настоящего момента учение Максвелла  продолжает развиваться и, можно сказать, каждый день приносит все новые и новые доказательства, подтверждающие теорию Максвелла. Общее признание теория получила после опытов Герца (см. электрические колебания), в которых удалось показать распространение электромагнитных волн, испускаемых источником электромагнитных колебаний, и которые во всех отношениях сходны со светом, т. е. преломляются, отражаются, поляризуются, интерферируют и т. д. и отличаются только отсутствием действия на глаз, а физически — размерами: волны у Герца 30—40 см, позднее у Лебедева 0,6—0,3 см, а световые 0,00007 до 0,00004 см. При дальнейшем развитии теории оказалось возможным объяснить явления поляризации (см.) при отражении, вывести вполне строго так называемые Френелевы формулы, определяющие поляризацию, а также интенсивность отраженных лучей, которые Френелем были выведены с некоторыми натяжками из  его старой теории. Далее были объяснены особенности металлического отражения, и установлена связь между показателями преломления и диэлектрической постоянной (см. электричество), между коэффициентом отражения света, т. е. долей всего падающего света, которая отражается, и электропроводностью отражающего света зеркала, т. е. установлены были соотношения между оптическими свойствами тел и электрическими, позволяющие по данным измеренным величинам предсказывать другие. Можно ли, идя по пути Герда и позднейших исследователей, получить волны световые и получить синтез света? Простой расчет показывает, что прибор Герца для этого пришлось бы сделать величиной с молекулу и даже меньше! Таким образом, для непосредственного доказательства электромагнитной природы света надо, оставив попытки синтеза света, исследовать готовые источники света. Результаты этих исследований составляют обширную главу, содержащую учение о так называемых магнито- и электрооптических явлениях. К этой категории явлений относится, прежде всего, открытое Фарадеем 1) явление вращения плоскости поляризации в магнитном поле. Если между полюсами сильного электромагнита поместить какое-нибудь прозрачное некристаллическое тело и пропускать через него плоско-поляризованный пучок света по направлению магнитных линий сил, то при замыкании тока в электромагните, т. е. при возбуждении магнитного поля, плоскость поляризации поворачивается так, что если до замыкания тока свет был погашен николем (см. поляризация), при замыкании появляется свет, и для затемнения надо повернуть николь на угол, равный величине магнитного вращения плоскости поляризации. От естественного вращения магнитное отличается тем, что направление вращения зависит от направления луча, т. е. от того, идет ли луч от северного полюса к южному или наоборот. Поэтому, если луч пройдет два раза через данное поле туда и назад, то вращение удваивается, тогда как в естественно вращающем теле, как, например, в кварце, при подобном расположении получается вращение, равное нулю. Теория этого явления основана на так называемой электронной теории (см.) и охватывает собой и более сложные виды явления, наблюдаемые в лучах, близких к тем, какие поглощаются испытуемым телом.

2) Земаново явление (см.).

3) Явление Керра состоит в том, что плоско-поляризованный луч становится эллиптически поляризованным при отражении от полированной поверхности электромагнита.

4) К электрооптическим явлениям относится явление двойного преломления, вызываемого электрическим полем в жидкостях, открытое Керром, и недавно открытая Штарком электрическая аналогия явления Земана.

Теория магнито - и электрооптических явлений, еще не вполне законченная, основывается на современном представлении о строении вещества, по которому каждый атом содержит в себе положительно  заряженное ядро и несколько отрицательно-заряженных частиц — электронов. Вследствие этих зарядов расположение и движение частиц находится под влиянием внешнего электрического поля. А если частицы находятся в движении, то, проявляя все признаки электрического тока, они, как электрический ток, подвергаются влиянию магнитного поля, изменяющего их движение подобно подвижному проводнику в магнитном поле. Особенно наглядно объяснение Земанова явления, данное Лоренцом (см. Земаново явление и электронная теория), а самый факт влияния магнитного поля на светящийся газ ясно указывает, что колеблющиеся частицы, вызывающие свет, должны быть электрически заряжены.

См. А. А. Эйхенвальд, «Акустика и Оптика» (М., 1914); Эдвин Эдсер, «Оптика» (СПБ, 1914); О. Д. Хвольсон, «Курс физики»; А. Г. Столетов, «Введение в акустику и оптику»; Р. Drude, «Lehrbuch d. Optik» (1912); В. Wood, «Physical Optics» (N.-York, 1911).

А. Тимирязев.

Табл. I

Табл. II