Тензориальное исчисление

Тензориальное исчисление. Векториальное исчисление (см. векториальный анализ) является чрезвычайно удобным орудием для исследования многих проблем геометрии, механики и физики, когда для описания явлений мы пользуемся, с одной стороны, трехмерным пространством, а с другой — выбираем прямоугольную и прямолинейную систему координат. Переход к криволинейным координатам и пространствам высших измерений заставляет соответственно изменить и обобщить векториальное исчисление, заменяя частный обычный вид векторов другим, более общим. Цель и назначение тензориального исчисления в этом обобщении и состоит.

Одно из основных свойств обыкновенного вектора заключается в том, что он не меняется, когда одну прямоугольную и прямолинейную систему координат меняют на другую, также прямоугольную и прямолинейную. Так, например, сила, действующая на точку и изображаемая вектором, не изменится, коль скоро мы перейдем от одной системы к другой. Таким образом, идея вектора связана с известной независимостью от избранной системы прямоугольных и прямолинейных координат. В соответствии с этим составляющие вектора в одной координатной системе должны определенным образом зависеть от составляющих вектора в другой координатной системе. Для обыкновенных векторов формулы преобразования их составляющих при переходе от одной такой системы K к другой будут

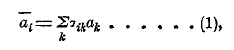
причем i и k пробегают ряд значений 1, означают соответственно составляющие вектора в системах и K; а_іk означает косинус угла оси і в системе с осью k в системе K; знак означает суммирование членов, у которых k пробегает ряд значений 1, 2, 3; как известно, a_іk удовлетворяют условиям

формулы преобразования координат при этом будут:

здесь х₁, х₂ и х₃ — координаты в системе K

Определение тензора. Тензориальное исчисление обобщает понятие вектора следующим образом.

Вместо специальных преобразований (2) возьмем любые точечные преобразования:

где функции однозначные и непрерывные функции переменных х₁, х₂, х₃, которые мы считаем какими угодно криволинейными координатами в трехмерном пространстве и обратно. Переход к пространству четырехмерному и высших порядков формально и очень просто достигается тем, что значок і, по которому суммируют или различают различные компоненты, пробегает только большее число значений, равное числу измерений; по существу, ни одно из приведенных ниже положений от этого не изменится; поэтому для упрощения обозначений и изложения мы ограничиваемся трехмерным пространством.

Если мы имеем тройку чисел Aⁱ которые при преобразованиях координат (3) преобразуются в новую тройку чисел по правилу:

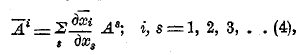
то тройка Aⁱ в своей совокупности называется когредиентным тензором первого ранга; составляющие такой тройки называются компонентами его и обозначаются обычно через какую-нибудь большую букву с индексом справа и наверху, например, Aⁱ.

Если тройка чисел преобразуется по правилу:

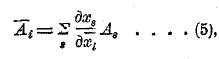
то тройка называется контрагредиентным тензором первого ранга, и его компоненты обозначаются через какую-нибудь большую букву со значками справа и внизу, например, A_i.

Термины контра- и когредиентный заменяются часто соответственно терминами ко- и контравариантный.

Самый простой пример когредиентного тензора первого ранга мы имеем в трех бесконечно малых приращениях трех координат:

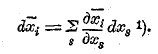
¹⁾  Когредиентный тензор dx₁, dx₂, dx₃ в виде единственного исключения из общего правила. Часто обозначается со значками внизу, т. е., пишется dx_i, а не dxⁱ, как следовало бы по общему правилу.

Пример контрагредиентного тензора первого ранга имеем в так называемом градиенте; в самом деле, если ψ —какая-нибудь функция координат, то градиентом ее по определению будет тройка чисел

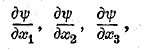
которая преобразуется в тройку

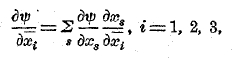
при переходе от координат x₁, x₂, x₃ к по формуле (5), т. е. точно так же, как А_i.

Скаляром в обычной теории векторов называют функцию компонент векторов, которая остается неизменной при преобразованиях (3). Такой функцией будет, например, внутреннее (скалярное) произведение двух векторов. По аналогии, обобщая, назовем скаляром или инвариантом функцию компонент тензоров, которая остается неизменной при любом преобразовании (3). Легко видеть, что

будет скаляром, т. е. легко доказать соотношение

Если мы имеем девятки чисел А^ik, A_ik илю А_i^k, которые при преобразованиях (3) преобразуются соответственно по трем правилам:

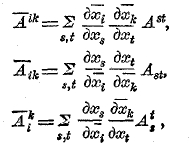
то такие девятки чисел получают название тензоров второю ранга, со специальным добавлением когредиентного в первом случае, контрагредиентного во втором и смешанного в третьем. Значки, поставленные справа наверху и внизу, показывают совершенно однозначно закон преобразования, компонент тензоров.

Данное определение легко обобщается для тензора любого ранга.

Алгебра тензоров. Получение новых тензоров посредством сложения, вычитания и умножения между собой различными способами компонент заданных тензоров составляет так называемую алгебру тензоров. Новые тензоры могут быть как более высоких, так и более низких рангов, чем исходные тензоры. Мы приведем здесь нескольк опримеров таких образований.

Пусть имеем тензор

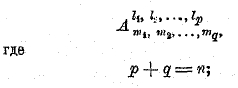
этот тензор имеет ранг n; он когредиентен в значках l₁, l₂, …, l_p и контрагредиентен в значках m₁, m₂, …, m_q.

будет тензором ранта q-s+p-t+u+v.

Примером приложения этой теоремы служат так называемое скалярное и векторное произведение двух векторов

В первом случае мы имеем понижение ранга по отношению к исходным тензорам, во втором — повышение. Несмотря на то, что тензор Т_іа второго ранга имеет девять компонент, с обычной векториальной точки зрения (для прямоугольных прямолинейных координат) мы все же имеем только три компоненты. Легко видеть, что у тензора Т_іа три компоненты Т₁₁=Т₂₂=Т₃₃=0, а три остальных удовлетворяют условию Т_іа = — Т_аі, т. е. попарно равны и противоположны по знаку, что соответствует понятию аксиальности векторного произведения двух полярных векторов.

Так как в выражениях, подобных (6), значки, по которым производится суммирование, всегда встречаются два раза — один раз вверху, а другой раз внизу, а значки, по которым не суммируется, только один раз— либо внизу, либо вверху, то знак суммирования ∑ часто опускают вовсе и его не пишут. Чрезвычайно простые правила пользования значками делают тензориальное исчисление особенно удобным орудием для вычислений.

Тензориальный анализ. Задачей тензориального анализа является получение новых тензоров посредством различных дифференциальных операций. Тензориальное исчисление вводит понятие некоторого вспомогательного тензора, который получает название фундаментального; это название дается ему ввиду того, что в некоторых специальных приложениях, например в дифференциальной геометрии а механике, этот вспомогательный тензор имеет основное  значение. В геометрии, например, он определяет собой характер трехмерного многообразия в квадратичной форме

в которой g_ik изображают его компоненты.

Обозначим контрагредиентный фундаментальный тензор через g_ik.

Можно доказать, что

где g детерминант из всех g_ik и Δ_іk его минор для члена с индексами і, k, будут компонентами когредиентного тензора.

Пусть имеем тензор А_i; можно показать, что

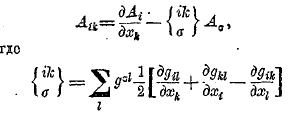
будет тензором второго ранга; можно доказать также, что

будет тензором второго ранга, но что

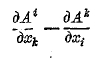
им не будет.

Как пример, заменяющий так называемре расхождение векторного анализа, можно указать на скаляр

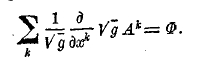
Можно было бы привести еще много других примеров образования тензоров дифференцированием.

Для получения дифференцированием новых тензоров вместо понятия фундаментального тензора вводят также весьма важное понятие тензориального параметра. Тензориальным  параметром называют величину, которая, подобно тензору, преобразуется при координатных преобразованиях по особому закону, а именно следующему

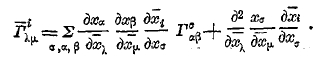
Можно показать, что

будет тензором.

Заметим, что с помощью тензориальных параметров можно получать тензора и иными способами. Выражения приведенные выше, представляют собой частный случай тензориального параметра.

Весьма большой интерес представляют те тензориальные образования, которые можно получить с одними тензориальными параметрами. Примером их будет тензор

он получил название тензора кривизны тензориальных параметров.

Если Г_ik^σ совпадают с то Fⁱ_kλμ получают название символов Римана второго рода. Из этих символов по правилу (6) легко получаются сокращенные символы Римана;

и затем так называемый скаляр кривизны Римана, получаемый применением той  же теоремы (6):

Этот скаляр получил название кривизны по тому смыслу, который он приобретает в геометрии двух измерений; так же, как и сокращенные символы Римана, он имеет весьма важное значение в общей теории относительности (см.) Эйнштейна.

Наконец, последнюю часть тензориального исчисления составляют его интегральные теоремы, которые являются соответствующими обобщениями теорем Стокса и Грина.

Курсы тензориального исчисления: В. К. Фредерикс и А. А. Фридман, «Основы теории относительности. Вып. I. Тензориальное исчисление», Лнгр. 1924; Я. И. Френкель, «Тензориальный и векториальный авализ», Лнгр., 1925.

В. Фредерикс.