Теория относительности
Теория относительности. I. Введение. В современной физике та ее часть, которая получила название принципа, или теории относительности, представляет собой прежде всего учение о том, как следует вводить в физику понятия времени и пространства в согласии с теми экспериментальными приемами, которыми принято пользоваться в настоящее время для их измерения. В этом учении устанавливаются физические понятия времени и пространства в отличие от различных чисто умозрительных представлений о них философов или математиков (например: пространство как форма чувственных восприятий в философии или пространство эвклидовой или неэвклидовых геометрий и т. д. в математике) и нередко даже в качестве вспомогательного методического приема и у самих физиков (например: «фазовое пространство» в статистической физике). Как доказывает анализ физических понятий пространства и времени, последние для своего описания требуют знания детого ряда особого рода величин, причем оказывается невозможным вполне отделить друг от друга понятия времени и пространства. О характере этих величин будет сказано ниже. Так как эти величины физические, то они должны подчиняться физическим законам, которые можно назвать основными, ибо они относятся к основным понятиям физики. Найти эти «основные» законы и дать им соответствующую математическую формулировку составляет последующую задачу теории относительности.
Современная физика стремится свести свои основные понятия к возможно-меньшему числу. В классической физике (т. е. в физике до создания теории относительности) к основным понятиям принадлежат понятия массы, энергии, электрического заряда, напряжений электромагнитного поля, тяготения и т. п. «Основной закон», данный Эйнштейном и связывающий пространственно–временные величины с массами, позволил ему без введения специальной силы тяготения дать объяснение явлениям тяготения; теория тяготения составляет третью задачу теории относительности.
Основной закон Эйнштейна не может считаться окончательным выражением того общего закона, которым современная физика стремится связать временно-пространственные величины с другими основными величинами физики. Существует тенденция не только свести к минимуму число основных физических величин, но даже сделать все их величинами производными из физических временно-пространственных величин. В создании одной общей геометрии для физических времени к пространства, объединяющей вое явления природы без специального введения других понятий, как электрический заряд, энергия, квант действия и т. п. состоит четвертая, еще невыполненная задача теории относительности.
II. К истории теории относительности. Специальная теория относительности. Исторически создание теории относительности сложилось следующим образом. В современном своем виде теории относительности является развитием, так называемой специальной теорией относительности которая в свою очередь явилась логическим завершением теории электронов Г. Лоренца (см. физика, XLIII, 335/43). Мы рассмотрим последовательно: 1) относительность классической механики в связи с некоторыми из ее начальных понятий, 2) специальный принцип относительности и затем уже, наконец, перейдем 3) к теории относительности современной физики, или к так называемой общей теории относительности.
Относительность в классической механике. Классическая механика предполагает существование абсолютного пространства и абсолютного времени. В абсолютном пространстве имеет место геометрия Эвклида. Абсолютное время понятие самостоятельное, не зависящее от пространственных представлений. От абсолютного пространства следует отличать относительные, которые движутся по отношению к нему. В относительных пространствах также имеет место геометрия Эвклида.
Классическая механика пользуется понятием массы и понятием силы. И то и другое могут быть названы абсолютными в том смысле, во-первых, что всякому телу или предельному понятию его — материальной точке, можно приписать некоторое число — «массу» m, всегда одно и то же, независимо от того, находимся ли мы в относительном, или в абсолютном пространстве; во-вторых, что силе мы также приписываем одну и ту же величину (некоторое число и направление) как в абсолютном, так и в относительном пространстве. Так, например, если координатные оси в относительном и абсолютном пространствах одинаково направлены, то слагаемые силы ![]() в обоих пространствах будут одинаковы. Это требование, предъявляемое к
в обоих пространствах будут одинаковы. Это требование, предъявляемое к ![]() и m, весьма, как мы увидим ниже, существенно.
и m, весьма, как мы увидим ниже, существенно.
Относительность классической механики следует из основного ее закона (см. движение, XVIII, 41/42):
![]()
где 02 ускорение точки с массой m, а ![]() приложенная к ней сила. Если мы положим, что оси координат в относительном и абсолютном пространствах одинаково направлены, и заметим, что в обоих пространствах
приложенная к ней сила. Если мы положим, что оси координат в относительном и абсолютном пространствах одинаково направлены, и заметим, что в обоих пространствах ![]() и m имеют одно и то же значение, то написанное уравнение тогда и только тогда приведет к одному и тому же решению его, когда аналитическое выражение для
и m имеют одно и то же значение, то написанное уравнение тогда и только тогда приведет к одному и тому же решению его, когда аналитическое выражение для ![]() будет одинаково. Но
будет одинаково. Но ![]() как легко видеть, будет одинаково только для пространств, которые двигаются друг относительно друга, и по отношению к абсолютному пространству прямолинейно и равномерно. Такие пространства или связанные с ними системы координат классическая механика называет «инерциальными»; равноценность инерциальных систем по отношению к уравнению (1) составляет содержание классического принципа относительности, или принципа относительности Галилея-Ньютона.
как легко видеть, будет одинаково только для пространств, которые двигаются друг относительно друга, и по отношению к абсолютному пространству прямолинейно и равномерно. Такие пространства или связанные с ними системы координат классическая механика называет «инерциальными»; равноценность инерциальных систем по отношению к уравнению (1) составляет содержание классического принципа относительности, или принципа относительности Галилея-Ньютона.
Если относительное пространство вращается по отношению к абсолютному, то выражение для ![]() будет другое; поэтому, чтобы получить то же самое движение с помощью тех же уравнений, как и для абсолютного пространства, надо к силе
будет другое; поэтому, чтобы получить то же самое движение с помощью тех же уравнений, как и для абсолютного пространства, надо к силе ![]() которая считается истинной, прибавить некоторую новую силу
которая считается истинной, прибавить некоторую новую силу ![]() как известно, для случая вращения это будет центробежная сила. Присутствие этой «кажущейся» силы
как известно, для случая вращения это будет центробежная сила. Присутствие этой «кажущейся» силы ![]() позволяет с точки зрения классической механики указать на опыте, вращается ли изучаемое относительное пространство по отношению к абсолютному, или нет; например, вращается ли земля вокруг оси, или нет.
позволяет с точки зрения классической механики указать на опыте, вращается ли изучаемое относительное пространство по отношению к абсолютному, или нет; например, вращается ли земля вокруг оси, или нет.
Абсолютное пространство, эфир и движение по отношению к нему. Таким образом, классическая механика позволяет обнаружить вращение по отношению к абсолютному пространству и не позволяет обнаружить движения поступательного и равномерного. Однако, существование абсолютного пространства, несомненно, должно иметь самостоятельный физический смысл, и изучение движения по отношению к нему должно было, поэтому, считаться весьма важным вопросом физики. Если механика, как таковая, не могла на него дать ответ, то можно было надеяться, что явления, непосредственно в круг ее рассмотрения не входящие, дадут нам этот ответ. Эту надежду поддерживало блестящее развитие, как с экспериментальной, так и с теоретической точек зрения, оптики и электродинамики в конце XIX столетия. С точки зрения физики конца XIX в. физическим осуществлением абсолютного пространства является эфир — носитель электромагнитного поля.
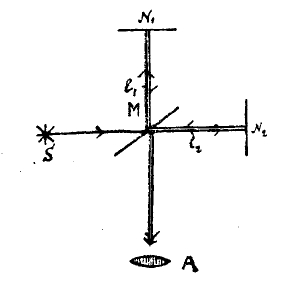
Рис.
Взаимоотношение между эфиром и обыкновенной материей в различных теориях электромагнитных и оптических явлений различно. Существуют две основные теории, выражающие два крайних взгляда на это соотношение: одна требует, чтобы эфир, находящийся в обыкновенной материи, был неразрывно с ней связан и двигался вместе с ней — это теория Герца; другая полагает, что материя движется через эфир, не увлекая его с собой и оставляя его неподвижным по отношению к абсолютному пространству — это теория Лоренца. Обе теории приводят к выводу, что поступательное движение по отношению к нему может быть обнаружено, и можно указать на целый ряд опытов, которые смогут послужить для этой дели; одним из примеров подобных опытов может послужить знаменитый опыт Майкельсона. Вот его краткое и схематическое описание: из S (см. черт.) выходит луч света; у полупрозрачного зеркала М он разделяется на два; один идет к зеркалу N1, и, отразившись от него и пройдя М, попадает в глаз наблюдателя А; другой идет к зеркалу N2 и затем возвращается, отражается от М и также попадает в глаз наблюдателя А. В глазу наблюдателя или фокальной плоскости объектива оба луча интерферируют (см. свет, XXXVII, 552 сл.). Результат интерференции зависит от длин l1 и l2 и скорости света по MN1 и MN2. Так как из S выходит расходящийся пучок лучей, то наблюдатель увидит систему интерференционных полос. Для центральной полосы разность хода лучей вычисляется очень просто.
Заметим, что с точки зрения теории Герца этот способ не может позволить обнаружить движение тела, так как эфир движется вместе с ним и скорость света по MN2 и MN2 одинакова; поэтому мы вычислим разность хода только с точки зрения теории Лоренца, т. е. неподвижного эфира. Пусть скорость света в абсолютном пространстве будет с; скорость земли будет v; прибор, будучи установлен на земле, участвует в ее движении. Если направление движения земли совпадает с ![]() то скорость света по
то скорость света по ![]() будет с—v, а по
будет с—v, а по ![]() будет с+v; время t2, нужное, чтобы пройти путь
будет с+v; время t2, нужное, чтобы пройти путь ![]() и обратно, будет:
и обратно, будет:
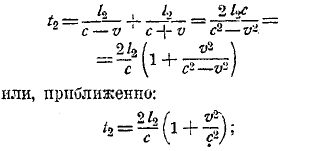
скорость света по ![]() одинакова и будет по правилу параллелограмма равна √c2-v2; время, чтобы пройти путь MN1 и обратно, будет:
одинакова и будет по правилу параллелограмма равна √c2-v2; время, чтобы пройти путь MN1 и обратно, будет:
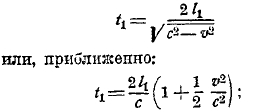
разность времен будет t2-t1, а соответствующая разность хода ΔN будет:
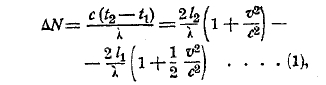
где N длина волны света.
Если мы повернем аппарат на 90°, то соответствующая разность хода будет:
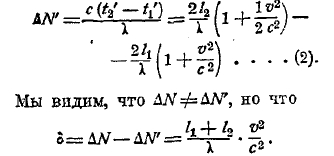
Как легко видеть, δ величина хотя и малая, но вполне доступная наблюдению. Таким образом, при повороте прибора на 90° разность хода ΔN для центральной полосы меняется. Из изменения δ разности хода и можно вычислить v, т. е. поступательную скорость земли относительно абсолютного пространства. Опыт дал отрицательный результат; смещения полос обнаружено не было. В первый раз этот опыт был произведен в 1881 г. Майкельсоном, затем был повторен несколько лет спустя Майкельсоном и Морлеем (1887) и затем еще раз повторен Морлеем и Миллером в 90-х годах. Весь этот ряд опытов был произведен приблизительно на уровне моря. Отрицательный результат в то время мог быть истолкован как подтверждение теории Герца. Можно было думать, что эфир, который должен по этой теории неразрывно двигаться вместе с землей, на больших высотах начнет понемногу отставать от земли; в этом случае опыт Майкельсона, повторенный на большей высоте, мог дать и положительный результат. Поэтому Миллер и повторил его (1923—1925) на высоте 1 300 м на горе Вильсон и действительно нашел небольшое смещение центральной полосы. Результаты наблюдений Миллера вызвали большие споры как с точки зрения правильности постановки опыта, так и с точки зрения толкования результатов. Большинство теоретиков признало, что наблюденное Миллером смещение полос не может быть объяснено движением земли относительно эфира. Более поздние опыты, произведенные независимо от Миллера на той же горе Вильсон физиком Кеннеди (1926) и затем Иллингвортом (1927), не обнаружили никакого смещения полос. Литература по вопросу этих опытов весьма обширна. Критический обзор возражений, делавшихся против теории опытов Майкельсона, можно найти у М. Лауэ (см. М. Laue, «Annalen der Physik» том 33, стр. 186, 1910 г.).
Все другие опыты, произведенные с той же целью, можно разбить на 2 категории. В одних определяется первая степень отношения скорости тела v к скорости света с, в других же вторая степень того же отношения. Можно установить, как общее правило, что в то время, как теория Герца удовлетворительно объясняла те опыты, в которых, как в опыте Майкельсона, определялась вторая степень этого отношения, и не объясняла те, где искалась первая степень его, — теория Лоренца, наоборот, объясняя первые, не объясняла вторых. Таким образом, электродинамика и оптика в своих попытках обнаружить поступательное движение к эфиру ни к каким вполне определенным результатам не пришли.
Теория Лоренца имеет некоторые особенности, которые отличают ее от классической механики. Как мы указали, классическая механика полагает, что компоненты истинной силы ![]() для всех инерционных систем одинаковы. В электродинамике мы встречаемся с понятиями напряжений магнитного электрического поля
для всех инерционных систем одинаковы. В электродинамике мы встречаемся с понятиями напряжений магнитного электрического поля ![]() которые мы склонны считать, как и силу классической механики, обыкновенными векторами. Между тем Лоренц нашел, что соотношения между
которые мы склонны считать, как и силу классической механики, обыкновенными векторами. Между тем Лоренц нашел, что соотношения между ![]() в двух системах, которые движутся друг относительно друга со скоростью v, но оси которых направлены параллельно друг другу, будут иметь для пустоты вид: .
в двух системах, которые движутся друг относительно друга со скоростью v, но оси которых направлены параллельно друг другу, будут иметь для пустоты вид: .
![]()
В этих формулах ![]() Соответствуют одной системе, а
Соответствуют одной системе, а ![]() другой. Другими словами, компоненты их, в отличие от компонента механической силы
другой. Другими словами, компоненты их, в отличие от компонента механической силы ![]() в различных системах различны.
в различных системах различны.
Кроме этих соотношений, обратим наше внимание на одно новое понятие, введенное Лоренцом, а именно — понятие о местном времени. Пусть t абсолютное время в абсолютном пространстве; если мы находимся в системе, которая движется со скоростью v по направлению, скажем, х-оси, то в движущейся системе гораздо удобнее пользоваться не абсолютным временем t, а величиной t*, которую Лоренц назвал местным временем и которая определяется из соотношения t*=t-vx/c2; здесь х расстояние от начала координат, причем предполагается, что в момент t=0 начала координат в движущейся и абсолютной системах совпадают. Это «местное время», как оказывается, стоит в тесной связи с фактически измеряемым временем. В самом деле, периодическое повторение какого-нибудь физического явления, например, появление какой-нибудь определенной звезды в меридианном приборе обсерватории, позволяет с легкостью определить время в каком-нибудь одном определенном месте. Если же требуется установить разность моментов времени в разных местах (точках) пространства, то вопрос усложняется; о том, что в одной точке А наступил момент времени, можно передать в другую точку В только с помощью какого-нибудь сигнала, на что требуется некоторое время, так как ни один сигнал не может быть передан мгновенно, но требует хотя бы и небольшого промежутка времени. Последний можно вычислить, если знать скорость передачи; но, чтобы знать скорость передачи, уже надо знать разность времен в двух точках. Получается заколдованный круг, из которого выхода без добавочной гипотезы не существует. Относительную скорость различных сигналов установить нетрудно; достаточно сигнал, вышедший из А и дошедший до В, вернуть немедленно обратно в А. Сигнал, вернувшийся раньше других, очевидно, передается быстрее других. Опыт показывает, что свет — самый быстрый из известных нам сигналов. Если по каким-нибудь соображениям считать, что свет идет от А к В и от В к А одинаково бистро, то можно измерить скорость света. Все опытные определения скорости света включают в себе эту предпосылку. Предположим, что она справедлива для абсолютного пространства или эфира; естественность такой гипотезы очевидна. Для эфира тогда можно установить разность времен для двух любых точек, а, значит, и установить понятие одновременности абсолютного времени в разных точках. Если мы движемся относительно эфира, скажем, вместе с землей по направлению х-оси, то в двух ее точках А' и В', совпадающих в какой-нибудь абсолютный момент времени с точками А и В абсолютного пространства, абсолютное время будет одним и тем же. Пусть t это время; пусть ![]() направление движения; вычислим момент прихода сигнала в В'. Скорость света в этом направлении, очевидно, равна с—v, а в обратном с+v. Если расстояние А'В' = х, то момент прихода в В' будет t’ = t + x/(c-v), а момент возвращения в
направление движения; вычислим момент прихода сигнала в В'. Скорость света в этом направлении, очевидно, равна с—v, а в обратном с+v. Если расстояние А'В' = х, то момент прихода в В' будет t’ = t + x/(c-v), а момент возвращения в
![]()
v очень мало по сравнению с с, и приближенно можно написать:
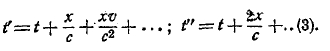
Таким образом, зная t, х, v, с, можно вычислить t’, т. е. определить приход сигнала из А' в В'. Предположим теперь, что у нас нет возможности определить v и с для абсолютного эфира, что, находясь на земле, мы измеряем скорость света таким же способом, каким только что определили ее для абсолютного эфира, т. е. с помощью гипотезы, что свет от А' к В' идет так же быстро, как от В' к А', со скоростью с*; тогда момент t* прихода света в B' будет по определению t* = t + x/c*, и момент обратного прихода в А' будет t” = t + 2x/c*. Сравнивая это и (3) мы видим, что с точностью до величин второго порядка по отношению к частному v/c, c* = c, но что t* = t’ – vx/c2; мы видим, что время t*, т. е. время, определенное в движущейся системе тем же физическим, приемом, как время t в абсолютной и покоящейся, связаны между собой как местное и абсолютное время Лоренца. Примером подобного экспериментального способа определения скорости света может служить известный способ Физо. В В установлено зеркало, а в А прибор для измерения времени. Если установить такой прибор сначала в покоящемся эфире и затем на двигающейся земле и считать, что он служит в том и другом случае для установления момента t’ прихода сигнала в В, по правилу t’ = (t+t”)/2, то соотношение между временем прихода в эфире и временем прихода на земле будет как раз соотношением между местным и абсолютным временем Лоренца. Можно ли, экспериментируя только на земле, установить разницу между местным временем и абсолютным? Разница для скоростей с* и с — второго порядка по отношению к v/c, поэтому те опыты, в которых ее можно обнаружить, должны быть очень точными, пример такого опыта мы видели в опыте Майкельсона, и результат его, как и всех других ему подобных, отрицательный.
В свое время Лоренц и одновременно с ним Фицджеральд, чтобы объяснить неудачу опыта Майкельсона, высказали предположение, что тело укорачивается в направлении движения в отношении √1-v2/c2. В самом деле, если мы в формулах (1) и (2) вместо l2 и l1 подставим соответственно l2√1-v2/c2 и l1√1-v2/c2 то получим δ = 0. Эта гипотеза, придуманная специально для этого опыта, не получила общего признания.
Совокупность всех указанных обстоятельств, т. е.:
1) невозможность установить скорость земли по отношению к эфиру,
2) соотношение между электрическими и магнитными силами в покоящейся и движущейся системах координат,
3) физический смысл «местного времени»,
4) гипотеза о сокращении тел по направлению движения,
нашла чрезвычайно удачное выражение. В формулированном Эйнштейном «принципе, или теории относительности», теперь называемой специальной теории относительности.
Основные допущения специальной теории относительности. Сделаем следующие допущения:
1) при переходе от одной координатной системы K к другой K’, двигающейся по отношению к первой прямолинейно и равномерно, местное время t одной заменяется местным временем t’ другой, по правилу:
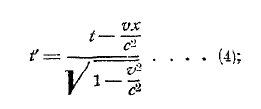
2) при замене одних координат х, у, z другими х', у', z' следует пользоваться формулами преобразования:
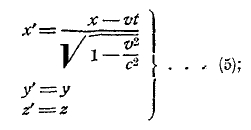
3) для пустоты1) между ![]() в системах К и К’ существуют соотношения:
в системах К и К’ существуют соотношения:
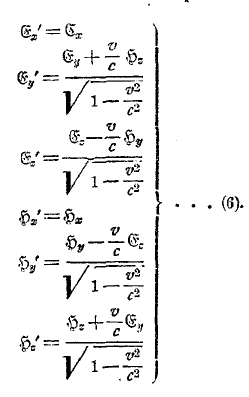
1) Мы ограничиваемся электромагнитным полем в пустоте, имея ввиду возможно большую краткость изложения; на самом деле следует принять в соображение поле и внутри материи. Мы предполагаем также, что скорость v направлена по х-оси, что не представляет собой никакого существенного ограничения.
Указанные допущения делают основные уравнения электродинамики совершенно одинаковыми в системах координат х, у, z и t и x', у', z' и t'.
Вследствие одинаковости этих уравнений поступательное равномерное движение не может оказать никакого влияния на ход опыта, и естественно поэтому, что опыт Майкельсона дает отрицательный результат. Основные уравнения для движущейся системы отличаются от выведенных Лоренцом из теории электронов и в предположении абсолютного эфира в членах второго порядка относительно v/c. Опыты, в которых определяется первая степень этого отношения, конечно так же хорошо объясняются теории относительности, как и теорией Лоренца.
Пояснения к сделанным допущениям. Скорость света — универсальная постоянная. Сделанные три допущения чрезвычайно важны по вытекающим из них следствиям. Если абсолютное пространство обнаружено быть не может, то все относительные пространства между собой равноправны, и местное время любого из них имеет столько же прав на признание его «настоящим» временем, как и время во всяком другом. Но местное время в данной системе определяется на основании вполне точно проведенного опыта в предположении, что скорость света в двух противоположных направлениях одинакова и что, какую бы мы координатную систему ни взяли, если мы только мерим время местным временем, скорость света с одинакова. Указанным способом измеряемая скорость света с делается, таким образом, универсальной постоянной. Если скорость тела v становится больше скорости света, то формулы преобразования (4), (5), (6) будут мнимыми и теряют физический смысл; мы видим, что скорость света имеет также значение предельной возможной скорости.
Вопрос об измерении длин также принимает иной смысл, чем раньше. Предположим, что какой-нибудь отрезок АВ измеряется с помощью линейки. Если отрезок движется, то при измерении его длины точки А и В должны рассматриваться в один и тот же момент времени; но один и тот же момент времени для двух точек в одной координатной системе вовсе не означает, что в другой, иначе движущейся координатной системе, моменты времени также будут одинаковы. Поэтому, говоря о длине отрезка, мы должны условиться, с точки зрения какой координатной системы мы его измеряем, или в какой координатной системе берем его точки А и В в один и тот же момент времени. Пусть Ko система, в которой отрезок АВ не движется, и пусть его длина в этой системе. Если рассматривать его теперь в другой системе K, которая движется по отношению к Ko то длина его, измеренная в K, будет зависеть от того, рассматриваем ли мы А и В в моменты одинаковые с точки зрения Ko, или одинаковые с точки зрения K. В первом случае длина его увеличится по сравнению с длиной в отношении 1/√1-v2/c2, а во втором уменьшится в отношении 1/√1-v2/c2. Можно было бы назвать длину, измеренную в Ko, истинной, а длины, измеренные по одному или другому способу, кажущимися, но такое название ведет часто к недоразумению. Утверждают, что, согласно теории относительности, тело сокращается по направлению движения, и спорят о том, истинное ли это сокращение, или кажущееся. На самом же деле, речь идет о том, чтобы произвести некоторый измерительный опыт, причем указывается, что в зависимости от того, каким способом введено время, результаты измерения должны получиться различные.
Но можно поставить вопрос о том, можно ли ввести в физику понятие длины, независимое от случайно выбранной координатной системы и ее движения. Здесь впервые возникает вопрос, который во всем своем значении выступает позднее в общей теории относительности. Координатная система, которой мы пользуемся для описания явлений природы, является по отношению к ее законам элементом более или менее случайным. Если нет абсолютного пространства и времени, то законы природы нужно формулировать независимо от выбранной системы координат, т. е. от некоторого случайного способа их описания. Математика в теории групп и теории точечных преобразований дает нам необходимые для этого средства. Можно показать, что выражение
![]()
будет инвариантом (см. тензориальное исчисление) по отношению к преобразованиям (4), (5).
Таким же инвариантом будет выражение
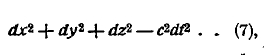
т. е. легко показать с помощью формул (4), (5), что
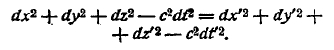
Квадратом элемента длины в обыкновенном пространстве будет
![]()
Рассмотрим разность dσ2-c2dt2; обозначим ее через ds2, если dσ2 > c2dt2 и через — dσ2, если dσ2 < c2dt2. Существует теорема, которую легко доказать и в силу которой в первом случае можно найти такую систему K’, чтобы ds2 = dσ2-c2dt2 = dσ’2, а во втором такую систему К”, чтобы dτ2 = c2dt2 — dσ2 = c2dt”2. Мы видим, что в первом случае инвариант ds2 имеет то же численное значение, как длина отрезка в системе K’, измеренная так, что оба его конца рассматриваются в одинаковые для этой системы, моменты времени (dt’ = 0); во втором случае инвариант dτ2 имеет значение времени в неподвижной для некоторой системы K” точке (dσ” = 0). В первом случае ds, а во втором dτ называют «собственной» длиной и соответственно «собственным» временем отрезка; на них и надо смотреть как на инвариантное определение длины и времени и нужно помнить, что «собственные» длина и время являются длиной и временем в обычном смысле этого слова только в особых координатных системах, так как, вообще говоря, выражения ds2 или dτ2 включают в себе квадраты приращений всех четырех координат х, у, z и t. Можно доказать весьма важную теорему, что если в одной системе с2dt2 > dσ2, то никакими координатными преобразованиями типа (4), (5) нельзя сделать так, чтобы dσ'2 > с2dt’2, или наоборот; другими словами, «собственное» время не может стать «собственной» длиной, и наоборот. Таким образом, мы видим, что пространство и время, будучи связаны вместе выражением для ds2 или dτ2, все же остаются в корне различными. Принцип причинности сохраняет свою силу.
Введенные Эйнштейном формулы преобразования координат и сил приводят к относительности только для поступательного и равномерного движения. Вращение продолжает играть ту же роль, как и в классической механике. Если исключена возможность определить поступательное движение по отношению к какому-то абсолютному пространству, то она остается для движения вращательного. Эта логическая недоделанность специальной теории относительности бросается в глаза, и естественно было искать выхода из этого положения; он нашелся в процессе дальнейшей критики опытного определений длины и времени и привел к установлению общей теории относительности.
Мы указали здесь важнейшие допущения специальной теории относительности; систематическое изложение основ ее читатель найдет в специальных трактатах и курсах.
III. Некоторые выводы специальной теории относительности. Четырехмерный мир Минковского. Возможность рассматривать инвариант ds2 = dx2 + dy2 + dz2 — с2dt2 как длину отрезка в четырехмерном пространнее привела Минковского к мысли рассматривать не только х, у, z и t как координаты четырехмерного пространства, но распространить четырехмерное толкование и на другие величины, характеризующие электромагнитное поле и материю в ее движении. Четырехмерное пространство, в котором четвертая координата время, Минковский назвал миром; точку в нем, в обычных представлениях означающую обыкновенную пространственную точку, рассматриваемую в какой-нибудь момент времени, мировой тонкой, или событием; четырехмерную линию он назвал мировой линией. Если отдельные элементы мировой линии представляют собою «собственное» время, то можно показать, что тангенс угла наклона ее к оси времен в любой точке меньше с; в этом случае мировая линия может служить в четырехмерном мире средством для изображения последовательных положений точки, движущейся в обычном трехмерном пространстве. Если тангенс угла наклона равен с, то легко найдем, что dτ = 0; из выражения (7) следует тогда, что скорость движения в трехмерном пространстве будет
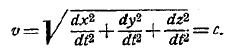
Таким образом, в мировой картине мировая линия, соответствующая распространению света, будет прямая, наклоненная к оси времен под углом, тангенс которого равен с.
Рассмотрим теперь главнейшие выводы специальной теории относительности, относящиеся к кинематике, динамике и электродинамике и отличающиеся от соответствующих выводов классической физики.
1) Кинематика. Формулы преобразования (4), (5) для перехода от одной координатной системы к другой позволяют вычислить скорость движения q' в одной из них, если известна скорость движения q в другой и относительная скорость обеих систем v. Если положить для упрощения внешней формы выкладок, но не упрощая задачи по существу, что vу = vz = 0 и что только vх ≠ 0, то легко найти из (4), (5), что
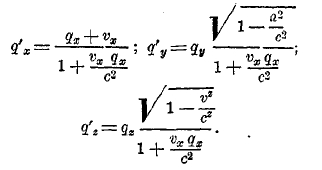
Эти так называемые формулы сложения скоростей заменяют классическое сложение по правилу параллелограмма, по которому
![]()
Новые формулы показывают, как и нужно было ожидать в связи с сделанными предпосылками, что скорость света является предельной скоростью также и в том смысле, что какие бы две скорости мы ни складывали, мы всегда подучим скорость меньшую, в крайнем случае равную, но никогда не большую скорости света с.
Кроме обычной скорости, специальная теории относительности рассматривает также так называемую четырехмерную скорость точки; пусть τ собственное время точки, т. е. длина ее мировой лилии, отсчитываемая от какой-нибудь любой из ее точек; тогда по определению четырехмерный вектор скорости имеет следующие компоненты
![]()
эти четыре компоненты не независимы друг от друга, но, как следует из (7), удовлетворяют соотношению:
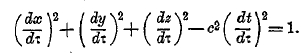
Из того же соотношения следует, что
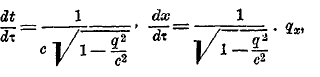
и т. д., где qх, qy, qz соответственно равны
![]()
представляют собою компоненты обыкновенной скорости, а q = √qx2 + qy2 + qz2 ee абсолютная величина. Четырехмерным вектором ускорения называют вектор
![]()
он имеет ту особенность, что его компоненты в четырехмерном мире «перпендикулярны» к вектору скорости; под перпендикулярностью здесь надо понимать соотношение, которое в геометрии с элементом длины (7) соответствует условию перпендикулярности в обыкновенной эвклидовой геометрии, т. е. геометрии с элементом длины ds2 = dx2 + dy2 + dz2 + dt2 для случая четырехмерного пространства. Простой подсчет показывает, что первые три компоненты четырехмерного ускорения не пропорциональны обыкновенному ускорению.
Обычное нам понятие объема так же, как и понятие длины, в специальной теории относительности перестает быть понятием инвариантным по отношению к движению. Если перед наблюдателем проходит со скоростью v объем V, то инвариантом по отношению к преобразованию Лоренца будет
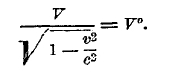
Величина V0 получила название «покоящегося» объема, что означает объем, измеренный в системе координат, в которой он не движется (v=0). В связи с этим находится понятие о «покоящейся» плотности. Пусть m0 масса тела, объем которого V0; его «покоящаяся» плотность ρ0 определяется из соотношения ρ0V0 = m0; для всякой другой системы можно написать
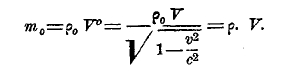
В этой системе получается как результат умножения
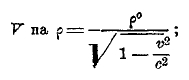
ρ получило название «движущейся» плотности.
2) Динамика. Основное соотношение Ньютона
m![]() =
= ![]()
должно было получить свое обобщение в специальной теории относительности, что и было сделано Пуанкаре и Минковским. Четвертая компонента вектора ускорения имеет ту особенность, что она может быть выражена через ее первые три компоненты и вектор скорости; если специальная теории относительности должна на место трех соотношений Ньютона поставить четыре новых, то зависимость четвертой компоненты вектора силы (а сила должна иметь теперь четыре компоненты, а не три) должна быть в такой же зависимости от своих первых трех компонент и вектора скорости, как и четвертая компонента ускорения. Только в этом случае можно установить, по аналогии с трехмерным законом Ньютона, пропорциональность между силой и ускорением. Если за четвертую компоненту силы взять работу силы в единицу времени, то, как оказывается, одинаковый характер четырехмерных векторов силы и ускорения будет установлен. Постулировав пропорциональность между ними и проинтегрировав затем по бесконечно малому объему, можно, как это и было сделано Минковским, написать четыре основных соотношения для движения материальной точки в таком виде:
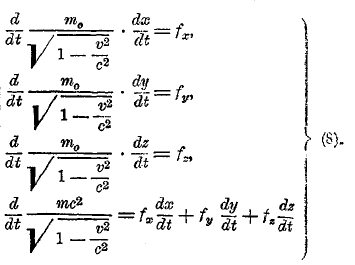
Первые три соответствуют ньютоновским
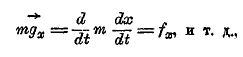
четвертое заменяет соотношение
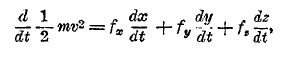
выражающее закон сохранения энергии. Ми видим, что различие для первых трех уравнений состоит в том, что в левой чаете этих уравнений вместо массы m0 стоит теперь выражение
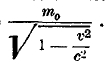
Если уcловиться называть это выражение количеством движения, то новые уравнения могут быть формулированы по старому: производная от количества, движения mv по времени равняется действующей силе. Можно называть также массой коэффициент, стоящий при ускорении; в таком случае масса также оказывается зависящей от скорости; исходя из уравнений (8) можно показать, что для продольного ускорения масса будет равна
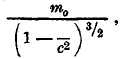
а для поперечного
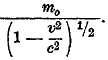
Зависимость инертной массы от скорости совершенно чужда классической механике. Опыты, главным образом Гюи и Лаванши, но также и других ученых, определявших отношение заряда к массе электрона при различных скоростях электрона, оказались в согласии с приведенными формулами и в противоречии с формулами классической механики и электродинамики, в которых кажущееся изменение массы электрона при изменении его скорости объясняется воздействием электромагнитного поля ра поле движущегося заряда е.
Четвертое из основных соотношений показывает, что в специальной теории относительности, вместо классического выражения для кинетической энергии материальной точки ½ mv2, мы имеем выражение
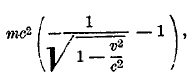
которое совпадает с классическим только в первом приближении, если отбросить величины порядка v2/c2 и меньше по сравнению с единицей.
Уравнения движения материальной точки в специальной теории относительности так же, как и в классической механике, могут быть получены из вариационных принципов.
3) Электродинамика. Формальное введение времени, как четвертого измерения, дало возможность написать основные уравнения электродинамики в чрезвычайно простой и симметричной форме. Инвариантность их для всех находящихся в поступательном и равномерном друг относительно друга движении координатных систем позволила решить в простой и элегантной форме и по одному общему методу целый ряд важнейших оптических и электрических задач для тел, находящихся в движении. Не имея возможности останавливаться на всех этих чрезвычайно интересных вопросах, мы коснемся здесь только нескольких новых фундаментальных понятий, введенных в физику специальной теории относительности.
Чрезвычайно важным для дальнейшего развития теории оказалось новое понятие тензора энергии и материи. Уже в классической электродинамике Максвеллом, а потом и другими учеными, было показано, что механическое действие электромагнитного поля на материю можно представить как результат действия особых напряжений в эфире; с точки зрения теории Максвелла эти напряжения должны быть, конечно, происхождения электромагнитного. Более поздняя теория электронов Лоренца прибавила к этой силе еще одну новую, равную отрицательной производной по времени от потока электромагнитной энергии (так называемого вектора Пойнтинга), разделенного на скорость света. Эта сила, равная изменению во времени некоторой величины, аналогична по форме силе инерции классической механики, которая в уравнения классической механики входит как производная по времени от количества движения. Абрахам назвал эту величину электромагнитным количеством движения (или импульсом).
Силу механического действия на единицу объема электрического заряда и работу ее в единицу времени можно рассматривать в специальной теории относительности как четырехмерный вектор. Ряд простых преобразований приводит выражение этой силы к точно такой же зависимости от напряжений Максвелла в пустоте и от электромагнитного количества движений, как и ранее для механической силы в теории Лоренца. Если мы возьмем замкнутую и изолированную систему, то применяя к ней первые три компоненты этого четырехмерного вектора и написав законы движения, мы получим по отношению ко всей системе закон сохранения ее общего количества движений, т. е. механического и электромагнитного вместе взятых; воспользовавшись же четвертой компонентой четырехмерного вектора, мы получим закон сохранения энергии. Знаменитый когда-то спор между Декартом и Лейбницем о том, сохраняется ли количество движений или живая сила, разрешается здесь одним общим и единственным законом.
Девять компонент тензора напряжений Максвелла вместе с шестью компонентами электромагнитного количества движений (из которых каждые две попарно равны по абсолютной величине и противоположны по знаку), к которым надо присоединить еще плотность электромагнитной энергии, составляют в общей своей совокупности шестнадцать величин; эти шестнадцать величин, как можно показать, являются в четырехмерном пространстве компонентами тензора второго ранга (см. тензориальное исчисление). Мы видим здесь, что в специальной теории относительности плотность энергии вовсе не представляет собой скаляр, как это можно было бы думать раньше. Если в одной координатной системе К0 плотность энергии не равна нулю, а равна, скажем, ω0, но поток энергии отсутствует (например, электростатически заряженный шар), то в другой системе К, движущейся со скоростью v относительно К0, поток энергии, или «количество движения», уже не будет равен нулю, но окажется равным плотности энергии в К0, разделенной на квадрат скорости света и умноженной на относительную скорость v обеих систем. Отсюда становится понятным один из замечательнейших выводов специальной теории относительности, а именно, что энергия, деленная на квадрат скорости света, оказывается эквивалентной в смысле своего механического действия некоторой массе m0; устанавливается соотношение m0 = ω0/с2. Эквивалентность энергии материи нашла в новой физике весьма много замечательных приложений. Указанный тензор второго ранга, в который энергия входит как составная часть, получил название тензора энергии и материи. Если считать, что природа вещей должна быть объяснена электромагнитным полем, то понятие этого тензора можно признать для физики фундаментальным, хотя его истинное выражение и нельзя еще считать известным.
4) Эфир. Специальная теория относительности отрицает возможность обнаружить абсолютное движение. Относительное поступательное движение двух систем может быть обнаружено в том случае, если у нас имеется возможность связать эти системы с двигающейся материей. Такие системы могут быть, например, связаны землей, солнцем и т. п. По представлению специальной теории относительности пространство между звездами, планетами и т. д. вовсе не пусто, ибо в нем, во всяком случае, находится излучаемая материей энергия, а энергия и масса эквивалентны. Специальная теория относительности утверждает только, что с этой, скажем, междузвездной массой или энергией мы на основании наших наблюдений не можем экспериментально связать никакой определенной системы координат, как можем это сделать по отношению к земле или к солнцу. Именно в этом смысле специальная теории относительности и утверждает, что эфир не существует, в противоположность эфирам Герца и Лоренца; в их теориях эфир всегда можно было связать с некоторой системой координат, которая в силу этого обстоятельства становилась абсолютной. Если считать эфиром не материю какого-нибудь исключительного свойства, «не материальную» в обычном смысле этого слова, как эфир оптики до появления электромагнитной теории света, а назвать эфиром энергию или эквивалентную ей массу, то такое понятие эфира вовсе не противоречит специальной теории относительности.
IV. Общая теория относительности. Как уже было сказано, основная идея теории относительности состояла в пересмотре способа введения в физику понятий пространства и времени. В схематизированной и в возможно более упрощенной форме этот способ состоит в следующем.
1) Многообразию действительно существующих вещей (с которым имеет дело физика) сопоставляется математическое многообразие точек четырех измерений. Это означает, что каждой физической вещи сопоставляются четыре числа: три числа отличают данную вещь от всякой другой по положению, четвертое — по времени. В четырехмерном математическом многообразии первые три числа, взятые отдельно, будут тремя пространственными координатами; вместе с четвертой (временем) они будут координатами точки четырехмерного пространства; мы их обозначим х1, х2, х3, х4. Сопоставление должно быть сделано так, чтобы оно было взаимно и однозначно; его можно назвать арифметизацией физического пространства и времени и практически оно сводится к введению какой-нибудь координатной системы для нахождения положения вещей и к указанию способа измерения времени в каждой точке координатной системы.
2) Такого рода арифметизированное физическое многообразие, если представить его себе в виде геометрического пространства, не имеет еще никакой геометрии. Следующий шаг физика состоит в том, чтобы определенным физическим явлениям, наблюдаемым в физическом многообразии, сопоставить в математическом многообразии определенные геометрические или временные понятия. Так, лучу света между двумя вещами, которым мы сопоставляем математическое понятие точек, можно сопоставить геометрическое понятие прямой; другим явлениям можно сопоставить геометрические понятия угла, площади, объема и т. д. Сопоставления эти произвольны так же, как и арифметизация пространства и времени; если можно пользоваться наравне с координатами прямолинейными координатами сферическими, цилиндрическими или еще какими-нибудь другими, то можно, например, считать за прямую не луч света, а натянутый шнур, край линейки и т. д.
3) Изучение математических многообразий точек и различных возможных в них геометрий привело к систематизации геометрий в зависимости от их свойств. Употребляя вместо слова многообразие слово пространство, говорят о пространствах постоянной, переменной, положительной или отрицательной кривизны; различают также пространства по их «связности», понимая под этим некоторое определенное изменение их свойств при переходе от точки к точке (см. топология); наконец, пространства различают по значению некоторых функций, входящих в так называемое выражение элемента длины или расстояния двух бесконечно близких точек:
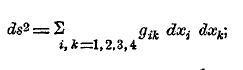
функции gik составляют тензор, обычно называемый фундаментальным, так как с его помощью характеризуются свойства пространства. Например, если gik имеют значение gik = 0 при i ≠ k и gik = 1 при i = k, то пространство будет обыкновенным эвклидовым (см. теоретические основания математики).
4) В арифметизированном физическом многообразии мы должны теперь выбрать такие явления, с помощью которых мы смогли бы ввести понятие об инвариантной длине ds. В математическом многообразии для достаточно малых разностей координат можно считать gik постоянными. Можно найти два таких физических явления, чтобы с их помощью физически интерпретировать элемент ds2 в тех двух случаях, когда или приращение четвертой координаты равно нулю, или приращение первых трех координат равно нулю. Первое явление будет масштабом длины, второе масштабом времени. Масштабом длины может быть длина волны света, длина метра эталона и т. д.; масштабом времени могут быть приняты любые часы, в частности, так называемые световые часы, т. е. луч света, бегающий взад и вперед между двумя параллельными зеркалами и своим постоянным возвращением к одному из зеркал измеряющий время.
5) Если в выражении для ds разности координат dxi двух любых точек, с одной стороны, и расстояние, или интервал времени, между ними, с другой — известны, то, взяв достаточное число точек по соседству с данной точкой, можно получить число уравнений, необходимое для вычисления в данной точке всех величин gik. Переходя от точки к точке, можно таким образом установить экспериментальные значения их для всего пространства. Опыт нам дает, что в пределах лаборатории и с точностью, определяемой ошибками наблюдения, значение gik соответствует эвклидовой геометрии, когда дело идет о трехмерном пространстве; специальная теории относительности показывает, что в пределах лаборатории для элемента длины в четырехмерном пространстве следует написать:
![]()
6) Опыт ничего не говорит нам, какие бы значения для gik мы получили, если бы мы могли измерять как достаточно малые, так и достаточно большие расстояния; равным образом, опыт ничего не может сказать о том, что лежит в пределах точности наблюдения. Теория Эйнштейна пробует закономерно связать значение функций gik с тем, что определяет собой все, происходящее в мире, т. е. с материей, и из этой связи найти их истинное значение и там, где грубый непосредственный опыт этого сделать не может. Косвенным подтверждением правильности найденных значений gik будет опытная проверка выводов теории.
7) Основные свойства физических тел — вещей физического многообразия — не могут, очевидно, зависеть от арифметизации физического пространства в таком же смысле, в каком события жизни не зависят от того, пользуемся ли мы в географии полярными или прямоугольными координатами. Математическое многообразие точек, сопоставленное физическому, может быть заменено другим с помощью другой арифметизации физического пространства. Переход от одного к другому аналитически может быть сделан с помощью соответствующего преобразования координат. Математика дает физику средства найти такие функции тензоров разных рангов, имеющих разное физическое значение, которые не зависели бы от случайно избранного способа арифметизации пространства и которые выражали бы свойства физических вещей, неизменные при каких угодно преобразованиях координат, в число которых входит и какое угодно движение. Специальная теория относительности привела к выводу, что материи может быть сопоставлен тензор энергии и материи. Этот тензор, как было указано, может и не иметь непременно того вида, который ему дала специальная теория относительности. Не предрешая его вида и обозначив его через Тik, основные соотношения Эйнштейна должно написать в виде соотношения между тензорами gik и Тik. Это соотношение должно быть написано в тензориальной форме, ибо только в такой форме оно удовлетворяет требованию независимости от случайного выбора координатной системы, т. е. общей относительности.
8) Исходным пунктом для Эйнштейна было известное из механики уравнение Пуассона
![]()
где ψ потенциал материи, плотность которой ρ. Обобщая его, Эйнштейн написал свои основные уравнения в таком виде:
![]()
где Rik и R функции от gik и их первых и вторых производных по четырем координатам и k постоянная, зависящая от выбора единиц. Функция R — так называемая риманова кривизна пространства. Функции Rik составляют шестнадцать компонент т. н. риманова тензора кривизны.
Эти основные уравнения, подобно основным уравнениям классической механики, могут быть выведены из вариационного принципа. Эти уравнения в первом приближении должны дать в пределах лаборатории геометрию Эвклида.
9) Если при Тik, наперед, заданных как функции координат и времени, основные уравнения служат для определения gik то, наоборот, известные gik позволяют определить Тik т. е. компоненты тензора энергии и материи; так как в число переменных входит и время, то тем самым определяется и движение материи. Таким образом, правильность зависимости gik от компонент тензора энергии и материи, т. е. от материи и ее движения, может быть подтверждена наблюдением над движением материи; например, в специальном случае солнца и земли соотношения, определяющие для них значение gik, должны дать и движение земли вокруг солнца. Таким образом, мы видим, что из основных соотношений (9) должны вытекать не только геометрические свойства физических пространства и времени, но и то, что в классической механике является следствием ее основных уравнений, т. е. закона тяготения, Эйнштейн показал, что, действительно, все то, что объясняется в классической механике силами тяготения, совпадает с тем, что в первом приближении вытекает из его основных уравнений, связывающих пространство и время с материей.
10) Классическая механика отличается от эйнштейновской еще и в следующем пункте. В уравнения движения материальной точки под действием силы тяготения ее масса входит два раза; один раз, как коэффициент инерции при ускорении, другой раз как причина, вызывающая силу тяготения. Это двойственное значение массы весьма замечательно. Еще Ньютон показал, что масса как коэффициент инерции, или так называемая инерционная масса, и масса, вызывающая тяготение, или тяготеющая масса, оказываются по данным наблюдениям равными. Более поздние и значительно более точные наблюдения показали с точностью до 1/30000000, что эти массы равны между собой. Классическая механика совершенно не касается вопроса причины равенства обеих масс. Заметим, что в уравнениях Эйнштейна масса выступает только один раз и именно в тензоре энергии и материи; таким образом, двойственность понятия массы в общей теории относительности отсутствует. Постулативное требование тождества обеих масс Эйнштейн поставил во главу своей теории. Оно получило название принципа эквивалентности.
Одно из следствий принципа эквивалентности это то, что центробежная сила по природе своей ничем не отличается от силы гравитационной; понятия «кажущаяся» и «истинная» силы теряют здесь свой смысл.
11) Весьма важным выводом теории относительности является форма уравнения движения материальной точки, так как основные уравнения классической механики написаны для точки. Можно показать, что в общей теории относительности движение материальной точки определяется уравнениями геодезических линий (т. е. линий кратчайшего расстояния) в четырехмерном пространстве, геометрия которого известна, коль скоро известны функции gik. Например, движение планеты вокруг солнца, причем планета, рассматриваемая как точка, находится таким образом: сначала вычисляются функции gik в предположении, что существует одна только очень большая масса солнца; затем находятся геодезические линии в четырехмерном пространстве, т. е. решается хорошо известная в вариационном исчислении задача; найденные таким образом геодезические линии с точки зрения трехмерного пространства представляют собой конические сечения с точкой, которая движется по ним по законам Кеплера. Когда длина четырехмерной геодезической линии становится равной нулю, то такие геодезические линии, называемые нолевыми, определяют собою распространение силы тяжести или света. Если учение о тяжести в общей теории относительности в первом приближении приводит к тем же результатам, как и старая теория, то во втором приближении можно предвидеть новые явления и пояснить некоторые уже известные, но еще удовлетворительно не объясненные явленна. Сюда относится: во-первых, движение перигелия Меркурия, во-вторых, смещение спектральных линий в поле тяготения в красной части спектра и, в-третьих, отклонение светового луча в достаточно сильном поле тяготения, например, около солнца. Предсказанные общей теории относительности новые явления были затем обнаружены опытом и находятся с ним в полном согласии.
12) Общая теория относительности позволяет включить в круг вещей, подлежащих ее рассмотрению, также и основные уравнения электродинамики, т. е. уравнения Максвелла-Терца. Оказалось возможным написать эти уравнения в форме инвариантной для каких угодно координатных преобразований в четырехмерном мире. Одним из чрезвычайно важных следствий этого является тождество скорости распространения тяготения и электромагнитного поля в пустоте. Для бесконечно малого участка пространства обобщенные формулы электродинамики всегда могут быть приведены к тому виду, какой они имеют в специальной теории относительности; таким образом, специальная теория относительности продолжает сохранять свое прежнее значение.
13) В свое время, до появления общей теории относительности, было сделано несколько попыток создать теорию материи в рамках специальной теории относительности; под теорией материи здесь следует понимать попытки объяснить существование отдельных электронов, атомных ядер и т. д. Эти теории дотерпели неудачу. Применение общей теории относительности вместо специальной не оправдало возложенных было на нее в этом отношении надежд, но привело в ряду попыток включить всю электродинамику в теорию физических пространства и времени. Сюда относятся работы Вейля, Эддингтона и самого Эйнштейна (1918—1927). Эти попытки также ни к какому окончательному результату не привели. Совершенно новый оборот в развитии теории квант, наступивший в 1926 г. после работ Борна и Иордана, Шредингера и др., заставил физиков еще раз признать необходимость пересмотра вопроса о введении в физику основных представлений о пространстве и времени, но вопрос этот до настоящего времени остается одной лишь программой.
Популярные очерка по теории относительности: О. Д. Хвольсон, «Теория относительности А. Эйнштейна и новое миропонимание», Лнгр., 1922; М. Борн, «Теория относительности Эйнштейна и ее физические основы», Лнгр., 1922; Э. Фрейндлих, «Основы теории тяготения Эйнштейна», 1924; Курсы на русском языке: Я. И. Френкель, «Теория относительности», Лнгр., 1923 . Курсы на иностранных языках: Н. Weyl, «Raum. Zeit. Materie». Berlin, 1924; А. S. Edgington, «Space, Time and Gravitation», 1920; его же, «The Mathematical Theory of Relativity», 1923.
В. Фредерикс.
| Номер тома | 41 (часть 7) |
| Номер (-а) страницы | 401 |
