Теория вероятностей

Теория вероятностей, отдел прикладной математики, имеющий своей задачей изучение случайных явлений и их применений к явлениям массовым (жизни общественной, естествознанию и т. д.).

Выражения «случайное событие» и «вероятность случайного явления» встречаются в разговорном языке человека, начиная с ранней поры его жизни и с ранней эпохи истории человечества. Но уяснение точного смысла этих понятий и установление научной теории, на них основанной, началось только с XVII в. Французский математик Лаплас, много способствовавший обработке основ теории вероятностей, говорил, что эта теория есть здравый смысл, сведенный к математическому исчислению. Этим он высказал, что теории вероятностей есть область прикладной математики, в основе которой лежит наблюдение над суждением по поводу явлений случайных и массовых. Отсюда видно, что та теория, о которой идет речь, имеет дело с двумя понятиями, на первый взгляд совершенно разнородными: 1) случайность, как, например, в азартных играх, 2) закономерность, наблюдаемая в жизни общественной и в природе. Эту двойственность смысла слова «вероятность» можно проследить, начиная с очень отдаленного времени, но только установление связи между этими понятиями завершает теорию и дает ей тот интерес и практическую пользу, которая обнаружилась особенно ярко только в последнее время.

Страсть к азартным играм, существовавшая издревле как в Европе, так и у народов Востока, приводила к попыткам подвести некоторые соображения под арифметический подсчет числа благоприятствующих и не благоприятствующих игроку статичностей, или шансов. Иными словами, пытались учесть вероятность ожидаемого выигрыша или проигрыша. С другой стороны, правители народов древнего Египта, евреев, греков и особенно римлян для практических государственных нужд делали попытки подсчета народонаселения, количества ежегодно собираемого хлеба или податей с тем, чтобы на этих данных основать расчеты на будущее время. Так, в VI в. н. э. в Дигестах, т. е. уложении Юстиниана, есть закон, из которого видно, что уже в то время римляне пытались установить среднюю продолжительность жизни. В  средние века в Италии появились морские страховые общества, для которых необходимо было установить вероятность кораблекрушения. В XVII в. итальянец Тонти первый основал предприятие, имевшее предметом страхование человеческой жизни: это предприятие получило название Тонтина.

Только что упомянутые попытки подготовили почву для теории. Истинными основателями ее были Паскаль и Ферма в XVII в. Толчком к развитию математической теории вероятностей послужил вопрос о безобидном разделе ставки между игроками до окончания игры, предложенный Паскалю. Таким образом, начало свое теории вероятностей получила в области применения к азартным играм. Всякая математическая теория имеет в своем основании одно или несколько положений, принимаемых за очевидные, из которых она затем развивается путем логических выводов. В чистой математике такие положения называются аксиомами, или постулатами; в науках прикладных это - законы, по возможности простые, найденные путем опыта или наблюдения. Теория  вероятностей, как уже было упомянуто, основана на наблюдениях над приемами суждения по здравому смыслу в применении к случайным явлениям. Чтобы подметить эти приемы, возьмем несколько простых примеров.

1) Происходит игра в орлянку. Бросается монета, по возможности правильная, имеющая на одной стороне герб, а на другой — надпись, или, как говорят, — орел и решетку. Один игрок держит пари, что выпадет орел, а другой — что выпадет решетка. При таких условиях шансы, на выигрыш у обоих игроков одинаковы. Мы скажем, что вероятность на выигрыш 1-го игрока и 2-го одинакова и равна ½. Сумма обеих вероятностей равна 1.

2) Бросается игорная кость в виде куба, по возможности правильно сделанного из однородного материала. Его грани перенумерованы цифрами от 1 до 6. Каждая грань имеет одинаковое число статичностей, или шансов на свое выпадение. Мы скажем, что вероятность на выпадение для каждой грани в отдельности равна 1/6.

3) Еще один типичный пример: в урне 10 шаров; из них 6 белых и 4 черных. Шары одинакового размера, одинаковы на осязание и тщательно перемешаны. Какова вероятность, что вынутый наудачу шар будет белый? Ясно, что здесь 6 шансов в пользу белого шара на 10 всех возможных шансов. Мы скажем, что вероятность вынутия белого шара равна 6/10, или 3/5. По такой же причине вероятность вынутия черного шара будет 4/10, или 2/5. Сумма обеих вероятностей будет 3/5 + 2/5 = 1.

Из приведенных примеров видно, что для измерения вероятностей мы считаем, сколько при условиях данной задачи существует всех возможных случаев, или статочностей, и сколько из них благоприятствует тому событию, о котором идет речь. Разделив число благоприятствующих статочностей, находим вероятность данного события. Само собой ясно, что все статочности должны быть равновозможными в том смысле, как в приведенных примерах: монета должна быть правильная, кость – тоже, шары в урне одинаковы и тщательно перемешаны.

Итак, вероятность мы измеряем дробью, у которой числитель есть число статочностей, благоприятствующих событию, а знаменатель – число всех возможных статочностей. Такая дробь – всегда правильная, за исключением двух крайних случаев: 1) когда все статочности благоприятствуют событию, 2) когда ни одна из них событию не благоприятствует. В первом случае событие достоверно, вероятность его равна 1, во втором случае событие невозможно, вероятность его равна 0.

Такие события, как выпадение орла или решетки при игре в орлянку, появление белого или черного шара при опытах с урной, называются событиями противоположными. Мы видим, что сумма вероятностей событий противоположных равна 1.

В простейших задачах счет числа статочностей производится непосредственно, как в приведенных выше примерах; в более сложных задачах пользуются известной из алгебры теорией соединений (см.), которая в значительной степени развилась вследствие запросов теории вероятностей. В задачах еще более сложных пользуются особыми теоремами, доказываемыми в теории вероятностей. Рассмотрим содержание двух простейших из этих теорем, причем их проверка по здравому смыслу производится легко. Первая из этих теорем называется теоремой сложения вероятностей и состоит в том, что в случае неравновозможных статочностей величина вероятности равна сумме вероятностей всех статочностей, благоприятствующих событию. Например, пусть в урну положено 12 шаров, не различимых на осязание и тщательно перемешанных; из них 5 красных, 4 голубых и 3 белых. Спрашивается, какова вероятность, что вынутый шар будет цветной. Непосредственным подсчетом, как в предшествующих примерах, видим, что вероятность красного шара равна 5/12, вероятность голубого 4/12; следовательно, по теореме сложения вероятностей, появление цветного шара имеет вероятность 5/12 + 4/12 = 9/12 = ¾, что поверяется и непосредственно, т. к. число цветных шаров равно 9.

Вторая теорема называется теоремой умножения вероятностей и позволяет вычислять вероятности т. н. сложных событий, т. е. представляющих собой совпадение нескольких событий, называемых простыми. Теорема говорит, что для нахождения вероятности сложного события, состоящего из нескольких простых событий, между собой независимых (т. е. таких, что осуществление или неосуществление одного из них не влияет на осуществление другого), надо перемножить вероятности этих простых событий. Например, в игре в орлянку появление орла 2 раза подряд есть событие сложное: вероятность каждого простого события (выпадение орла) равна ½; на основании теоремы умножения вероятность двухкратного появления орла ½ · ½ = ¼. (Результат можно проверить и непосредственно; число всех статочностей при двухкратном бросании монеты — 4: орел, орел; орел, решетка; решетка, орел; решетка, решетка). Если в урну положено 6 белых и 4 черных шара, то появление при первом испытании белого шара, а при втором черного будет событием сложным; вероятность его на основании теоремы умножения будет равна 6/10 · 4/10 = 0,24. Такой результат вполне понятен с точки зрения здравого смысла: сложное событие менее вероятно, чем каждое из простых событий, его составляющих. Естественно, что вероятности простых событий приходится перемножать: произведение правильных дробей меньше каждой из них в отдельности.

Кроме теорем сложения и умножения, теории вероятностей дает ряд теорем и методов решения разнообразных задач. В основе их лежит только одно выведенное из наблюдений условие — оценивать вероятность события отношением числа статочностей. В таком виде теория не нуждается ни в каких дальнейших постулатах или аксиомах, кроме тех, которые лежат в основе всей чистой математики вообще. Но вместе с тем возникает вопрос: какой же реальный смысл имеют те дроби, которые мы называем величинами вероятностей? Они, конечно, могут привлекать внимание и интерес математиков со стороны метода их вычисления, но реальное значение для практиков они получат только тогда, когда мы с ними свяжем конкретное содержание. Здесь мы встречаемся с другой группой вопросов, которые выдвинулись гораздо раньше первых основ теории вероятностей, но получили свое разрешение позже, и которые в последнее время возбудили особенно большой интерес по своему значению в науках общественных и биологии.

Опять обратимся к примерам с орлянкой и урной. Наблюдая, как выпадает монета у игроков при игре в орлянку, мы заметим, что появление орла и решетки чередуется самым причудливым образом; но, сосчитав число орлов и решеток после большого числа партий, мы заметим, что число тех и других почти одинаково, т. е. число орлов и решеток почти равно ½  всего числа бросаний. Чем бросаний больше, тем ближе это число к ½. Так же точно, если в урне 6 белых шаров и 4 черных, то после очень большого числа вынутий, причем предполагается, что каждый вынутый шар возвращается в урну, число отмеченных появлений белого шара будет близко к 6/10, т. е. 3/5 всего числа испытаний.

Такую дробь, как отношение числа появлений белого шара к числу всех испытаний, числа появлений орла к числу всех бросаний монеты, вообще числа появлений события к числу всех наблюдений, — мы тоже в обыденной речи называем вероятностью. Математики называют ее вероятностью а posteriori, статистики — частостью. Ежедневный опыт и многочисленные испытания показывают, что вероятность а posteriori, или частость, очень близка к вычисленной заранее изложенными выше способами дроби, называемой, в отличие от только что названной величины, вероятностью а priori. Чтобы получить некоторое понятие о близости обеих величин: частости и вероятности, рассмотрим таблицу, приводимую в сочинении Пирсона, где даны величины частости, найденные различными лицами, производившими испытания над явлениями с вероятностью ½.

Род испытания	Частость	Число испытаний	Лицо, производившее испытание
Рулетка	0,5015	16141	Pearson
Рулетка	0,5027	16019	De Whalley
Урна с шарами	0,504	4096	Quete’st
Урна с шарами	0,5011	10000	Westergaard
Монета	0,51	4040	Buffon
Монета	0,5005	4092	De Morga’s pupil
Монета	0,5004	8178	Griffith
Монета	0,5016	12000	Pearsons
Монета	0,5005	24000	Pearsons
Монета	0,50034	7275	Westergaard

Чтобы проверить, будет ли частость столь же близка к вероятности, когда вероятность далека от ½, рассмотрим таблицу Чубера для вышедших номеров лотереи в Праге и Брюнне. При каждой игре из колеса, содержащего в себе 90 номеров, вынимается по 5. Можно заранее вычислить вероятность того, что из вынутых 5 номеров число однозначных номеров равно: 0, 1, 2, 3, 4, 5. Для тех же случаев можно найти частость по опубликованным бюллетеням. Получилась следующая таблица:

Число однозначных номеров	Вероятность	Частость для лотереи
		В Праге (число испытаний 2854)	В Берлине (число испытаний 2703)
0	0,58298	0,58655	0,57899
1	0,34070	0,32656	0,34591
2	0,06989	0,07919	0,06881
3	0,00619	0,00735	0,00629
4	0,00023	0,00035	0,00000
5	0,00000	0,00000	0,00000
	1	1	1

Отождествляя частость с теоретической вероятностью, мы опираемся на опыт, т. е. поступаем так же, как и во всех опытных науках. Но так же, как и там, мы должны постараться свести опытную основу к наиболее простому закону, который соответствовал бы роли, занимаемой аксиомой в чистой науке.

Обращаясь к опыту не только искусственно поставленному, но и к опыту повседневной жизни, мы видим, что события с очень малой теоретической вероятностью встречаются на практике так редко, что мы с ними не считаемся, рассматривая их как невозможные. Например, если в урне на 1 000 000 шаров положен 1 черный шар, а остальные белые, то всякий скажет, что, вынув наудачу шар из урны, нельзя ожидать черный. На такое же основание опирается наша уверенность в наступлении завтрашнего дня, наша уверенность в неизменности законов природы: уверенность в завтрашнем дне основана только на том, что до сего времени солнце ежедневно всходило, незыблемость законов природы не была поколеблена ни одним научно установленным случаем.

В приложениях теории вероятностей принимается как постулат невозможность встретиться с событием, вероятность которого очень мала, например 0,001 или 0,0001 и т. д. Малость этой дроби зависит от строгости той науки, к которой мы хотим применить теорию. Важно то, что мы признаем существование такой дроби. Как только это принято, — все теоремы и формулы теории вероятностей получают реальное содержание и обширное применение ко всем т. н. массовым явлениям.

Основанием этой области теории вероятностей служит теорема Якова Бернулли, позволяющая установить границы возможного уклонения частости от вероятности. Яков Бернулли 20 лет обдумывал доказательство своей теоремы, но она была опубликована в сочинении «Ars conjectandi» только в 1713 г., спустя 7 лет после смерти автора, его племянником Николаем Бернулли. Впоследствии она была значительно обобщена Пуассоном, предложившим для этой обобщенной теоремы название «закон больших чисел». Далее, она была еще обобщена академиком П. Л. Чебышевым  и разрабатывалась с различными видоизменениями условий многими математиками.

Наиболее давнее из приложений теории вероятностей, основанных на теореме Якова Бернулли, есть ее приложение к вопросу о безобидности игр и к теории страхований. Пусть некоторое лицо участвует в игре, где величина выигрыша равна А руб., а вероятность на его получение р; пусть это лицо, сыграв s партий, выиграло из них m. В таком случае вся выигранная им сумма равна mА руб., что составит в среднем по m/s А руб. на каждую партию; т. к., согласно теореме Бернулли, при весьма большом s величина m/s частости очень близка к вероятности р, то можно сказать, что средняя величина выигрыша на 1 партию при данных условиях равна Ар. Эта величина называется математическим ожиданием игрока при данных условиях. Для того, чтобы игра была безобидна, игрок перед началом игры должен уплатить устроителю игры ставку, равную средней величине выигрыша, иначе говоря, математическому ожиданию. На этой же формуле основывается и теория страхования (см. ХLI, ч. 4, 709/12), расчеты пенсионных касс, эмеритур и т. д. В самом деле, на страховую премию можно смотреть как на выигрыш, причем делаемый страхователем взнос есть его ставка. Теория страхований есть дальнейшая разработка подробностей этой основной мысли.

Чтобы уяснить в коротких словах сущность доказательства теоремы Бернулли, обратимся к типичному примеру. Пусть производятся испытания над появлениями белых и черных шаров из урны, где вероятность появления белого шара равна р, а черного q, причем каждый раз после вынутия шара он возвращается в урну, и шары перемешиваются. Обозначим буквою s число всех испытаний, а буквами m и n числа появившихся белых и черных шаров. Вероятность такого сложного события (появления белого шара m раз и, следовательно, черного n раз) обозначим буквою Р_m. При этом ясно, что m+n = s и р+q = 1. Так как при каждом новом испытании вероятность события не зависит от результатов предшествующих испытаний, то величину Р_m можно вычислить, применяя упомянутую выше теорему умножения вероятностей и формулы теории соединений. Получится следующее:

Из алгебры известно, что эта формула есть общий член бинома (р + q)^s. Следовательно:

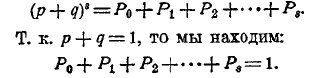
Все слагаемые в левой части положительны, следовательно, все они меньше 1.

Черт. 1.

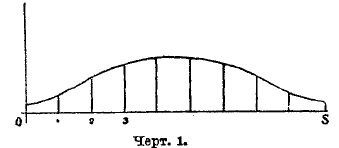
Чтобы составить себе наглядное представление об этих членах, прибегнем к графическому способу. На горизонтальной прямой (оси абсцисс) отложим от начала координат 0 отрезки, равные 0, 1, 2, … s, — так называемые абсциссы; в конечных точках их восставим перпендикуляры (ординаты), соответственно равные: Р₀, Р₁, Р₂..  Р_s. Соединив конечные точки ординат, получим ломаную линию, выражающую закон вероятностей сложных событий при s испытаниях.

Какие бы примеры мы ни брали, мы всегда заметим, что крайние точки ломаной имеют ординаты очень малые, в средней части ломаной есть одна вершина, лежащая наиболее высоко над осью абсцисс: ордината ее наибольшая, а от этой точки влево и вправо ординаты вершин уменьшаются (черт. 1). С увеличением s, протяжение ломаной по оси абсцисс беспредельно растет, ординаты же ее вершин уменьшаются, т. к. сумма их остается постоянно равной 1, а число ординат s+1 увеличивается.

Вершины ломаной составляют ряд отдельных точек; для уяснения особенностей в их расположении и для более простого способа вычисления их ординат проводят плавную аналитическую кривую, близко подходящую к вершинам ломаной. Строя такую кривую, приходим к уравнению:

где е — основание Неперовых логарифмов, равное е=2,71828..., π —известное из геометрии число = 3,141592..., h — независящий от m параметр, определяемый равенством:

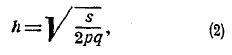
а х — переменная величина, выражающаяся через m равенством: х = m/s—р.

Т. к. m/s есть отношение числа появлений белого шара к числу s всех испытаний, т. е. частость появления белого шара, а р — вероятность появления белого шара, то х есть уклонение частости от вероятности, величину которого нам надо рассмотреть, чтобы судить, в какой мере частость можно считать за приближенную величину вероятности. Т. к. выражение (1) есть вероятность того, что m равно данной величине, то эта же формула выражает вероятность того, что уклонение равно данному числу x.

Рассматривая кривую (1), видим, что наибольшая величина ее ординаты соответствует значению х=0, причем она равна h/s√π. Следовательно, наивероятнейшая величина уклонения х есть 0, а потому наивероятнейшее значение m есть sp. Наивысшая точка кривой (1) соответствует абсциссе х = 0, начиная от этого места, в обе стороны ординаты точек кривой (1) уменьшаются и тем быстрее, чем больше h. Чтобы иметь некоторое наглядное представление о виде кривой (1), на черт. 2 изображены такие кривые: 1) для h = 1, 2) для h = 2. Мы видим, что при увеличении h кривая делается более вытянутой по оси ординат и быстрее спускается к оси абсцисс; точки кривой более тесно группируются около оси ординат и менее рассеяны на плоскости. Это выражают словами: чем больше h, тем меньше дисперсия точек кривой. С увеличением h вероятности малых значений x увеличиваются, а больших — уменьшаются.

Черт. 2.

Если мы положим в формуле (1) переменное х равным ряду последовательных значений от —а до +а и результаты сложим, то по теореме сложения вероятностей получим в сумме вероятность того, что уклонение х лежит между —а и +а. Интегральное исчисление дает средство вычислить эту сумму и показывает, что она зависит только от величины ha. Она выражается символом Ф(ha). Для вычисления этой величины составлены таблицы функции Ф(х), прилагаемые в курсах теории вероятностей. Чтобы дать некоторое понятие об этих таблицах, приведем из них небольшую выписку:

Х	Ф(х)	Х	Ф(х)
0,00	0,0000 000	2,50	0,9995 930
0,50	0,5204 999	3,00	0,9999 779
1,00	0,8427 008	3,50	0,9999 9925 691
1,50	0,9661 052	4,00	0,9999 9998 458
2,00	0,9953 223	4,80	0,9999 9999 999

Из нее видно, что величина функции Ф(х) при х малом имеет значения, близкие к 0, но, по мере увеличения х, она быстро растет, приближаясь к 1; уже при х, равном 3,6, она разнится от Х меньше чем на 0,9999 99 и при дальнейшем увеличении х продолжает приближаться к 1. Припомним сказанное выше, что в приложениях теории вероятностей заранее делают условие считать за 1 всякую дробь, которая больше чем 0,999 или 0,9999 и т. д. Обозначим буквою с такое число, чтобы Ф(с) равнялось выбранной дроби, например, Ф(с) = 0,9999. Величину с находим из сказанной таблицы; так, из равенства Ф(с) = 0,9999 найдем с = 2,76. Принимая за достоверное событие с вероятностью 0,9999 или больше, мы в праве сказать, что уклонение а не может превзойти величины, определяемой равенством ha = с, т. е. величины а=c/h. Так как h определяется равенством h=√s/2pq, то мы видим, что величина а = c/h при s весьма большом будет очень мала, т. е. мы с достоверностью можем утверждать, что разность между частостью m/s и вероятностью р не превзойдет очень малой величины c/h. В этом состоит теорема Якова Бернулли. Величина c/h называется крайним возможным пределом уклонений; чем он меньше, тем меньше будет ошибка, которую мы сделаем, принимая частость за величину вероятности. Поэтому h называется мерою точности.

В виде примера приложения теоремы Бернулли возьмем один из опытов, упомянутых в приведенной выше таблице (опыт Вестергаарда): в урну положено 20 белых и 20 черных шаров, и из нее произведено вынутие шара 10 000 раз, причем белый шар появился 5 011 раз. В таком случае р = q= ½, m/s = 0,5011, уклонение m/s – p = 0,5011 – 0,5 = 0,0011. Мера точности h =141, 421; положив с равным 2,6, можем сказать, что а = 0,0195. Наблюденное в действительности уклонение m/s – p = 0,5011 – 0,5 = 0,011 не превосходит этого предела. Многочисленные подобные же проверки постоянно подтверждают справедливость формулы.

Мы до сих пор предполагали, что над урной произведено один раз большое число s испытаний, причем событие (появление белого шара) произошло m раз, частость его равна m/s, а уклонение частости от вероятности равно х = m/s – p. Такой ряд испытаний назовем серией испытаний. Пусть таких серий сделано k, причем k тоже число очень большое, и все серии испытаний произведены при одинаковых условиях; величины получившихся уклонений мы обозначим так: х₁, х₂, х₃,..., х_k. Обозначим буквой σ выражение:

Эта величина называется средним квадратическим уклонением частости от вероятности при данных условиях. На основании приведенных выше формул можно показать, что при весьма большом k величина h выражается через σ формулою:

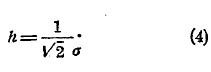
Если бы почему-либо величины h мы не знали, но могли бы из наблюдений над появлением шара по формуле (3) найти σ, то формула (4) дала бы нам приближенную величину h. В теоретических выводах, о которых мы сейчас говорим, такого случая не встретится, но в практических вычислениях часто приходится пользоваться формулою (4) для вычисления h.

В предшествующих рассуждениях мы говорили о примере урны с определенным числом белых и черных шаров, причем это число во все время испытаний не меняется. Само собою понятно, что рассуждения останутся в силе и при всяких других опытах (с монетою, игорною костью, рулеткою), лишь бы в этих опытах существовала основная вероятность (как вероятность появления белого шара), постоянная во всех испытаниях.

Как только теорема Бернулли была доказана, явилась мысль об ее обобщении на случаи, когда вероятность в течение опытов меняется. Первый шаг в этом направлении принадлежит Пуассону. По его мысли, для каждого испытания берется соответствующая ему урна; вероятность появления белого и черного шара в 1, 2, 3, . .s урне суть: p₁, q₁; р₂, q₂;…;  p_s, q_s. Обозначив буквою m число белых шаров, вышедших при всех испытаниях, можем снова назвать отношение m/s частостью.

Возникают вопросы: 1) какова наивероятнейшая величина частости, 2) какова вероятность уклонения х отдельной частости m/s от этого наивероятнейшего значения и 3) каков возможный предел уклонения этой частости. Результаты оказываются следущие: 1) наивероятнейшая величина частости есть среднее арифметическое из вероятностей появления белого шара в отдельных урнах:

эта величина называется средней вероятностью; 2) вероятность Рm данной величины m, или, что то же, соответствующего уклонения х = m/s – p, в большинстве случаев приближенно выражается формулою:

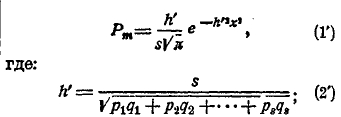
3) обозначая буквою с такое число, что Ф(с) можно принять за единицу, найдем, что уклонение х не может быть больше, чем c/h’. При большом числе s величина h’ весьма велика, поэтомуcнайденный предел c/h’ очень мал. Этот результат носит название теоремы Пуассона, иначе она называется законом больших чисел. По этой теореме уклонение частости от средней вероятности при пуассоновых условиях будет равняться очень малой величине. Сравнивая выражения (2) и (2'), найдем что h' > h; следовательно, уклонение в пуассоновых условиях меньше, чем в условиях Бернулли. Когда р₁ = р₂ = р₃ = … = p_s = p, и мы получим теорему Бернулли как частный случай пуассоновой.

Следующее после пуассоновой и сравнительно простое обобщение теоремы Бернулли дается такой задачей: в урну положено весьма большое число М шаров белых и черных в таком отношении, что вероятность появления белого шара равна р, а черного q. Из этой урны вынимаются шары по одному; но каждый вынутый шар в урну не возвращается. Зададимся теми же вопросами, как в предшествующих задачах, удерживая соответствующие обозначения. Находим следующее: 1) наивероятнейшее значение частости m/s равно вероятности р вынутия белого шара при начале испытаний, 2) вероятность Р_m уклонения x = m/s – p равна:

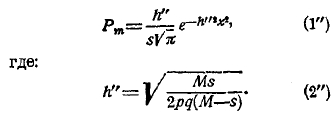
Т. к. h” > h, то опять приходим к выводу, что уклонения в данной задаче еще меньше, чем в предшествующих.

Кроме рассмотренных случаев, были исследованы и некоторые другие, причем вероятность Р_m выражается такой же показательной формулой, как (1), (1’), (1”), но мера точности различная. Она определяется из условий задачи.

Статистика выдвигает вопросы иного рода, хотя и сходные с предшествующими. Образно можно характеризовать их так: природа подает нам для испытания различные урны, состав которых нам неизвестен. Находя из опыта частость в ряде серий, мы хотим сделать заключение о характере исследуемого явления. Обыкновенно случается, что величины частости, найденные из ряда серий испытаний, весьма близки между собою и группируются около своего среднего арифметического, которое имеет по своим свойствам большое сходство с вероятностью. Оно поэтому и называется статистическою вероятностью. Обозначая его буквою р и вычитая его из отдельных частостей, находим уклонения x₁, х₂, …, х₃ частостей от вероятности р. Найдя эти величины уклонений, вычисляем величину:

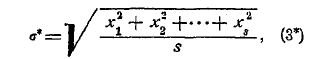
называемую средним квадратическим уклонением, а затем находим величину h* по формуле:  

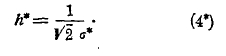
Вероятность Р_m частости — выразится формулою:

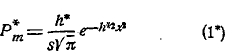
Припомним, что чем больше мера точности, тем теснее точки кривой группируются около оси ординат, тем дисперсия ее меньше. Формула (1*) такого же характера, как в рассмотренных выше задачах теоретического характера, где есть вероятность основная или средняя. Поэтому, естественно, возникает вопрос: можно ли в данном случае статистическую вероятность р рассматривать как основную или среднюю. Если р основная вероятность, то, как мы знаем, мера точности должна выражаться формулою:

Кривую с мерой точности (2) мы назовем кривой с нормальной дисперсией. Сравним ее с кривой (1*). Если h*=h, то кривая (1*) имеет дисперсию нормальную; если h* > h, то дисперсия кривой (1*) меньше нормальной, кривая имеет дисперсию поднормальную если h* < h, то дисперсия сверхнормальна. Во всех изученных до сего времени случаях, даваемых статистикой, дисперсия оказывалась сверхнормальной или в редких случаях близкой к нормальной.

Лексис, положивший начало исследованиям этого рода, назвал h* физикальной величиной, h комбинаторной величиной меры точности; отношение Q = h/h*, называется коэффициентом расхождения. Ясно, что при Q = 1 дисперсия нормальная, при Q > 1 она сверхнормальна, когда Q < 1 — поднормальна. Один из самых давних и подробно разработанных вопросов есть вопрос о рождении мальчика. На основании публикуемых сведений о числе родившихся детей можно найти отношение числа родившихся мальчиков к числу всех новорожденных в данной стране за данное время. Это число обладает исключительным постоянством. По вычислениям Лексиса, для различных округов Пруссии оно равно 0,515; коэффициент расхождения оказывается равным 1,09. Дисперсия почти нормальная. (См. статистика, XLI, ч. 4, 413/34).

В вопросах, до сих пор рассмотренных, мы говорили о тех случаях, где может наступить одно из двух противоположных событий (например, появление белого или черного шара, орла или решетки и т. д.); попутно мы встретили вопрос о вероятности величины уклонения частости от вероятности: мы измеряем вероятность приближенной величиной, а именно — частостью, и определяем величину вероятности той ошибки, которую мы сделаем, принимая частость равную вероятности. Ясно, что это — частный случай в вопросе более широком: о приближенном вычислении какой бы то ни было величины и о вероятности ошибки при полученном результате измерения. Эта теория ошибок измерения впервые опубликована Гауссом в 1809 г.

Он положил в основание начало арифметической средины: наивероятнейший результат из системы измерений, произведенных при одинаковых условиях (равноточно), есть среднее арифметическое. Вероятность, что ошибка при измерении заключается между ε и ε+dε, где dε величина очень малая, выражается так:

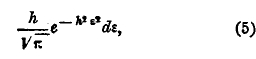
где h есть мера точности. Для нахождения этой величины мы поступаем следующим образом. Пусть неизвестная величина х измерена s раз, причем получились величины x₁, x₂, …, x_n. Наивероятнейшее значение х поначалу арифметической средины есть их среднее арифметическое

Принимая его за истинное значение измеренной величины, находим ошибки при полученных результатах измерения:

Составляя выражение по тому же типу, как выше выражение (3), находим:

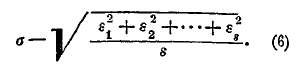
Это — средняя квадратическая ошибка для полученных измерений. Выражение:

есть величина параметра h в формуле (5), т. е. мера точности измерения.

На этих формулах основана обширная и стройная Гауссова теория ошибок измерения. Качество отдельного измерения характеризуется мерой точности h или средней квадратической ошибкой σ. Кроме того, часто вычисляют величину r, называемую вероятной ошибкой. Это — такое число, относительно которого с одинаковым правом можно утверждать, что ошибка больше или меньше его. Величина r определяется формулой

Мера точности среднего арифметического ξ равна h√s, следовательно, она в √s раз больше меры точности отдельного измерения.

Па теории ошибок Гаусса основан и способ наименьших квадратов, предложенный Лежандром, но строго обоснованный Гауссом. Задача этого способа — нахождение наиболее надежных величин для неизвестных, когда непосредственно измерить их мы не можем, а измеряем только величины выражений, куда эти неизвестные входят. Получается ряд уравнений, содержащих в себе искомые величины, как неизвестные. При этом число уравнений должно быть по возможности велико, — во всяком случав больше числа неизвестных. Т. к. в уравнения входят величины, найденные измерением, т. е. приближенно, то между уравнениями непременно будут противоречия. Задача способа наименьших квадратов состоит в нахождении для неизвестных таких числовых значений, при которых противоречия были бы как можно меньше.

Бельгийский математик и антрополог Кетле, изучая размеры одного и того же органа, в частности роста, у различных людей, нашел большое сходство в особенностях полученных им результатов с теми, которые обнаруживаются при рассмотрении результатов измерения одного и того же предмета. Он пришел в мысли, что природа, создавая человека, имеет ввиду осуществить определенный нормальный образец, и только вследствие случайных причин делает уклонения от этого образца. Если эта мысль верна, то понятно, что уклонения в размерах каждого органа у отдельных людей от среднего образца должны следовать тому же закону, который обнаруживается для ошибок измерения в гауссовой теории. Применение гауссовой теории привело Китле к созданию основ теории массовых явлений, или т. н. математической статистики. В большинстве своих исследований Кетле пользовался приведенной выше формулой Гаусса, и она давала ему результаты, согласные с действительностью, вследствие чего закон, выражаемый этой формулой, получил название нормального закона. Но уже сам Кетле обратил внимание на то, что нормальный закон окажется ошибочным, если исследуемый материал — не однороден.

В основе теории кассовых явлений лежит понятие о кривой распределения. Для его уяснения возьмем пример, с которого Кетле начал изложение своей теории. Пусть речь идет о росте солдат определенного полка. Разделив весь промежуток, в котором встречается человеческий рост, на малые интервалы, положим в 1 дюйм, мы записываем, сколько из измеренных солдат приходится на каждый из этих интервалов. Конечно, карликов и великанов будет немного, а чем ближе мы будем подходить к среднему росту, тем чаще будут встречаться люди, к нему принадлежащие. Таблицу, где в одном столбце в последовательном порядке написав рост, в другом столбце — против каждого роста соответствующее число солдат этого роста, мы назовем таблицею распределения солдат данного полка по росту. Подобным же образом можем составить таблицу распределения рабочих в данном городе и в данном году по заработной плате; распределение умерших в данном городе и в данном году по их возрасту; распределение цветков данного вида растений в данной коллекции по числу лепестков на них, и т. д. Отдельные предметы, вошедшие в счет, обыкновенно называются объектами, все эти объекты вместе взятые называются совокупностью, число объектов совокупности — объемом совокупности, а та величина, которая положена в основу распределения (рост солдат, заработная плата и т. д.) называется признаком объекта. Для составления наглядного понятия о характере изучаемого распределения пользуются графическим приемом: берутся две взаимно перпендикулярные оси координат на горизонтальной оси (оси абсцисс), от начала координат откладываются отрезки, изображающие величину признака, а из конечной точки каждого отрезка в виде ординаты откладывается длина, выражающая число объектов с этой величиной признака. Соединив конечные точки ординат в последовательном порядке прямыми линиями, получим ломаную, выражающую закон изучаемого распределения. Обыкновенно, как мы это видели, говоря о росте солдат, ординаты крайних точек слева и справа в построенной ломаной будут очень малы, по мере приближения к средней части ломаной ординаты увеличиваются до некоторой наивысшей точки ломаной. Ломаная имеет такой же характер, какой мы нашли, рассматривая члены бинома при выводе теоремы Бернулли. Отрезок оси абсцисс между крайними ординатами называется базисом ломаной, абсцисса наивысшей точки ее — модой.

Обозначив абсциссы вершин ломаной буквами: x₁, x₂, …, x_n, соответствующие им ординаты буквами y₁, y₂, …, y_n а объем совокупности (число его объектов) буквою N, составим выражение:

Это — средняя величина признака для объектов данной совокупности.

Кроме величины ξ в теории распределения имеют большое значение величины, представляющие обобщения этой величины, а именно:

где k — какое угодно целое положительное число. Это — так называемый момент k-го порядка. При k = 1 выражение m_k. т. е. m₁, равно величине ξ, следовательно, средняя величина признака равна моменту 1-го порядка. Начало координат соответствует тому значению признака, от которого мы начинаем отсчитывать его величину; например, рост человека можно отсчитывать или от 0, или от некоторого числа дюймов, соответствующего наименьшему встречающемуся у человека росту. Поэтому начало координат в значительной мере выбирается произвольно. В зависимости от изменения начала координат меняются и величины моментов. В теории кривых распределения оказывается целесообразным перенести начало координат в точку с абсциссой ξ. Эта точка называется центром распределения, а моменты, вычисленные для случая, когда величины признака отсчитываются от центра, называются центральными; будем их обозначать буквой М_k, где k равно 2, 3, 4,... (величина M₁ равна 0). Чтобы не вводить новых букв, будем обозначать величину признака, отсчитываемую от центра, прежнею буквою x; она будет положительна, когда признак объекта больше среднего, и отрицательна, когда он меньше среднего. Величина х есть уклонение признака в отдельном объекте от среднего значения. Момент 2-го порядка выразится так:

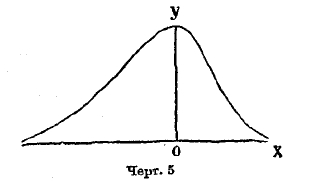
Квадратный корень из этой величины М₂ называется средним квадратическим уклонением для дайной совокупности объектов: σ = √М₂. При изучении закона распределения в простейших случаях, впервые встреченных Кетле, как упомянуто выше, можно считать величину х за случайное уклонение признака от средней величины его, служащей как бы образцом. Поэтому естественно, что линия распределения выразилась формулой, подобной формуле Гаусса:

Эта кривая симметрична относительно оси у; поэтому центр распределения лежит в начале координат, а наивысшая (модальная) точка лежит на оси у (черт. 3).

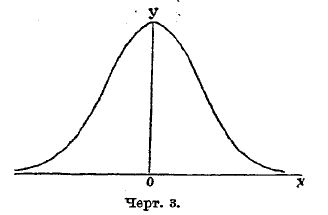
Черт. 3.

Как заметил уже Кетле, в случаях более сложных кривая распределения может быть асимметрична: мода ее разнится от абсциссы центра. Форма кривой распределения такого более общего вида представлена на черт. 4.

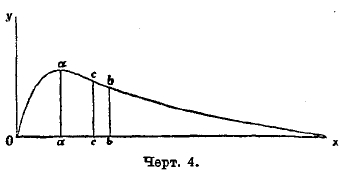
Черт. 4

Хотя возможность встретить асимметричную кривую была указана Кетле, но уяснение характера таких кривых и нахождение вида их уравнения принадлежит английскому современному математику Пирсону. Чтобы составить уравнение кривой распределения в более общих случаях, чем гауссов, Пирсон обратился к задаче теории вероятностей, составляющей ближайшее обобщенно той, которая приводит к формуле бинома, а именно: он берет тоже знакомый нам случай с урной, где вынутые шары в урну не возвращаются. Этот случай Парсон назвал гипергеометрическим вследствие особенностей членов того ряда, который встречается в этом случае. Откладывая по оси абсцисс величину частости, как в случае бинома, а на перпендикулярах к ней величины членов получаемого ряда, находим опять ломаную. Плавная кривая, наиболее близко подходящая к этой ломаной, и есть кривая Пирсона. Общий вид уравнения этой кривой таков:

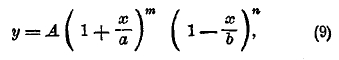
где А, а, b, m, n суть постоянные числа. Величины их определяются по моментам линии распределения, вычисляемым описанным выше способом. Для определения 5 параметров А, а, b, m, n надо найти объем совокупности и моменты первых 4 порядков. В зависимости от величин этих моментов, параметры могут получать различные значения: положительные, отрицательные, действительные или мнимые, конечные или бесконечные. В связи с этим формула уравнения и вид соответствующей кривой могут быть весьма разнообразны. Кривые Пирсона делятся на 7 классов, определяемых так называемым критерием Пирсона:

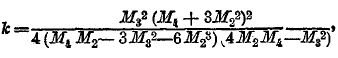
где М₂, М₃, М₄ суть центральные моменты.

Черт. 5.

Черт. 6.

Черт. 7.

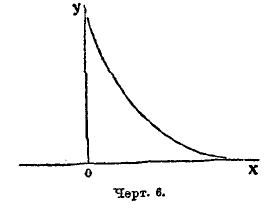
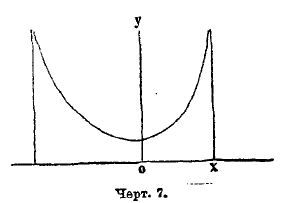
Если k < 0, то кривая принадлежит к типу I; она выражается уравнением (9), где все параметры действительны, m и n больше чем —1, переменное х получает значение между —а и +b; следовательно, длина базиса кривой а+b конечных размеров. Если   показатели m и n положительны, то ординаты конечных точек кривой равны 0, кривая имеет такой вид, как на черт. 5; если m отрицательна, а n положительна, то ордината кривой при начале базиса равна бесконечности. Кривая имеет такой вид, как на черт. 6. Наконец, когда m  и n отрицательны, то ординаты при обоих концах базиса равны бесконечности; кривая имеет такой вид, как на чертеже 7. Случай распределения этого типа представляют наблюдения в Бреславле над распределением дней года по степени облачности. Не входя даже в беглый обзор других типов кривых по системе Пирсона, т. к. это завяло бы много места, заметим, что при k=0 и, кроме того, М₃ = 0, кривая Пирсона принадлежит к типу VІI и есть нормальная кривая, т. е. кривая Гаусса (8); следовательно, эта кривая, приведшая Кетле к основам созданной им теории массовых явлений, входит в классификацию Пирсона как частный случай. Разрабатывая свою теорию, Пирсон приложил ее к весьма сложной кривой смертности. При этом он обнаружил, что кривая смертности может быть разложена на 5 кривых его типов, соответственно 5 родам смерти: 1) младенческого возраста, 2) возраста детского, 3) юношеского, 4) зрелого, 5) старческого. Из них 1, 2 и 5 принадлежат к типу III, а 3 и 4 — нормальные. Кривая младенческой смертности начинается на ¾  года раньше рождения (мертворожденные) и имеет начальную ординату равную бесконечности. Это – результат теоретического вывода, совершенно неожиданный и с первого взгляда парадоксальный; но он станет понятным, если вдуматься, какое множество человеческих жизней гибнет еще до рождения и в первые дни после рождения.

В рассмотренных случаях мы говорили о распределении совокупности по одному признаку (например, людей по росту). Но возможно обобщить это понятие и говорить о распределении по двум или нескольким признакам, например, людей по росту и объему груди или по росту, объему груди и силе руки, и т. д. Или же можно рассматривать сложный объект, например, отец и сын, и распределять такие сложные объекты по двум признакам: росту отца и его сына. Мы будем говорить пока только о распределении по двум признакам. Это понятие приводит к открытию новой области, называемой теорией корреляций.

В чистой математике постоянно приходится пользоваться понятием «функция». Если две переменные величины х и у связаны между собой так, что каждому данному значению х соответствует одно или несколько значений у, то у называется функцией х. Такое понятие постоянно встречается в приложениях математики к механике, физике, астрономии и т. д. Но в статистике встречается зависимость иного характера, например, рост отца и его сына. Обыкновенно, т. е. в среднем, у отцов высокого роста бывают сыновья роста большого, а у отцов низкорослых и сыновья невысокие. Отсюда заметно, что некоторая зависимость между ростом отца и сына есть; но по росту отца нельзя вычислить рост сына, т. к. этот рост допускает большие колебания; встречаются даже случаи (правда, редкие), когда у отца высокого роста сын оказывается низкорослым. Можно только говорить о среднем росте сыновей для отцов данного роста. Зависимость этого характера называется корреляционной зависимостью, или, коротко, корреляцией. Для простоты рассуждений будем иметь ввиду частный пример корреляции между ростом отца и сына: это один из самых давних примеров, разработанных Пирсоном. Обозначим один признак (рост отца) буквой х, а другой признак (рост сына) буквой у. Возьмем прямоугольные оси координат и примем х за абсциссу, а у за ординату точки на плоскости. Каждому объекту дайной совокупности соответствует определенная точка. Все эти точки составляют поле точек; число их равно объему совокупности, который мы обозначим буквой N. Во всех примерах, даваемых статистикой, поле точек, построенных указанным образом, имеет характерную особенность: оно напоминает кучу песка, насыпанного на горизонтальный лист бумаги через узкое отверстие: в той части плоскости, которая расположена под этим отверстием, песчинки скучены очень тесно около некоторого центра, по мере удаления от центра песчинки встречаются все реже, пока, наконец, не перестают встречаться совершенно. В большинстве случаев, а именно, когда признаки х и у между собой связаны корреляционно, поле точек не представляет округлую форму, оно несколько вытянуто в определенном направлении и имеет форму овальную (эллиптическую). Эта форма стоит в зависимости от характера и степени связи между признаками.

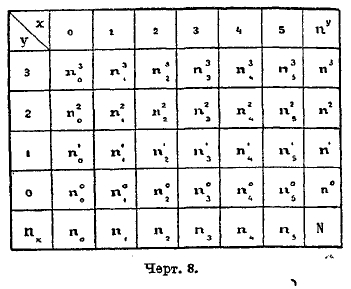
Покроем плоскость, занятую точками поля, сетью прямоугольников по возможности малых размеров и со сторонами, параллельными осям координат. Сосчитаем число точек поля для каждого из этих прямоугольников и запишем на каждом прямоугольнике это число лежащих в нем точек поля, называемое численностью для данного прямоугольника. Если в каком-либо прямоугольнике точек поля нет (прямоугольник пустой), то численность его равна 0. При таком условии сеть прямоугольников будет представлять собой прямоугольную таблицу, все клетки которой имеют свою численность, если принимать во внимание и численность, равную 0. Пусть левая нижняя вершина некоторого прямоугольника имеет координаты х, у; такой прямоугольник будем называть прямоугольником (х, у). Если измерения прямоугольника весьма малы, то все точки поля, лежащие внутри него, имеют координаты очень близкие к х и у; приближенно примем их равными х и у, а численность прямоугольника обозначим буквой n^y_x. Для ясности рассуждений схематически на черт. 8 изобразим таблицу численностей, так называемую корреляционную таблицу.

Черт. 8.

Числа, стоящие в одном и том же вертикальном столбце, называются строем, в частности х-вым строем, если он соответствует абсциссе х. Так же точно числа одной и той же горизонтальной строки назовем горизонтальным строем, в частности у-вым строем. Сложив числа х-вого строя, получим число, которое обозначим через их и назовем численностью х-вого строя. Все такие числа составляют добавочную строку внизу таблицы. Таким же образом, сложив числа у-вого строя, получим численность n^y. Эти числа составят добавочный столбец справа таблицы. Сумма чисел добавочной строки так же, как и добавочного столбца, равна объему N совокупности. Составим сумму всех произведений вида xn_x ; разделив ее на N, получим среднюю величину признака x для объектов данной совокупности. Обозначим ее буквою ξ. Таким же образом вычислим среднюю величину η признака у. Точка с координатами (ξ, η) называется центром распределения. Для упрощения вычислений переносим начало координат в центр (ξ, η), а оси оставляем параллельными прежним. Для избежания излишних обозначений мы будем обозначать координаты центральные (для нового начала) прежними буквами х и у. Тогда х и у будут обозначать уклонения об их средних значений. Говоря о распределении по одному признаку, мы видели, что характер распределения может быть весьма разнообразен, но наибольшей простотой и распространенностью в приложениях отличается нормальное распределение, выражаем с формулой Гаусса. Обобщая это определение, мы назовем нормальным такое распределение по двум признакам, где все строи горизонтальные и вертикальные, а также добавочная строка и столбец представляют собою числа, следующие нормальному распределению. Восставим в левой нижней вершине каждого прямоугольника сети перпендикуляр к плоскости и отложим на нем длину, равную численности прямоугольника. Если измерения прямоугольников малы, то конечные точки перпендикуляров будут между собой близки, они определяют некоторый свод над горизонтальной плоскостью. Чтобы определить форму этого свода, мы составляем уравнение аналитической поверхности, близко проходящей к конечным точкам построенных перпендикуляров. При нормальном распределении это уравнение таково:

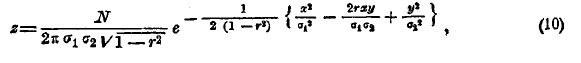
где σ₁ среднее квадратическое уклонение для чисел добавочной строки корреляционной таблицы (черт. 8), а σ₂ —  среднее квадратическое уклонение для чисел, стоящих в добавочном столбце той же таблицы. Обе величины вычисляются тем способом, который мы видели, говоря о распределении по одному признаку. Величина r вычисляется несколько сложнее; поэтому опускаем подробности этого вычисления, ограничиваясь тем, что скажем о нем ниже. Величина r называется коэффициентом корреляции. Из формулы (10) непосредственно видно, что не может быть больше 1: иначе величина √1—r², входящая в формулу (10), была бы мнима; следовательно, r заключается между —1 и +1. Из той же формулы (10) следует, что величина r имеет наибольшее значение, когда х и у равны 0; следовательно, поле точек наиболее густо при центре распределения, что соответствует сказанному в самом начале. Мы знаем, что все строи, в том числе и х-вый строй, имеют нормальное распределение; следовательно, наибольшая густота точек поля в прямоугольниках х-вого строя находится при центре этого строя. Чтобы исследовать распределение для х-вого строя, положим в формуле (10) переменное х равным данному числу и будем считать в этой формуле изменяющимся только у. Получится формула распределения гауссова типа; в ней координата центра распределения выразится формулою:

а среднее квадратическое уклонение в этом строе:

Формула (11) показывает, что центры распределения всех вертикальных строев лежат на одной прямой, выражаемой уравнением (11) и проходящей через центр всего распределения. Она называется прямой регрессии. Формула (12) есть среднее квадратическое уклонение каждого вертикального строя около его центра, лежащего в пересечении этого строя от прямой регрессии. Из формулы (12) видно, что рассеяние точек для всех вертикальных строев одинаково и растет с уменьшением r по абсолютной величине. Оно наибольшее, когда r = 0; в этом случае величина (12) равна σ₂, т. е. среднему квадратическому уклонению признака у для всего поля. В этом случае зависимости между величинами у и x: не существует, т. е. корреляции нет никакой. Когда r увеличивается, величина (12) уменьшается, точки поля располагаются плотнее около линии регрессии; наконец, при r = ±1 величина (12) обращается в 0, все точки поля сдвигаются на линию регрессии, следовательно, у есть функция от х, определяемая прямою (11) при r = ±1, т. е.

Отсюда ясно, почему величина r названа коэффициентом корреляции; она измеряет силу корреляционной зависимости; когда r=0, зависимости не существует; чем больше r по абсолютной величине, тем зависимость сильнее; при r = ±1 зависимость полная, функциональная.

Рассуждения, которые мы делали о вертикальных строях, можно применить и к строям горизонтальным: 1) центры горизонтальных строев расположены на одной прямой:

проходящей через центр всего распределения, 2) среднее квадратическое уклонение каждого горизонтального строя около центра, т. е. около его пересечения с прямой регрессии (11'), одинаково для всех горизонтальных строев и равно:

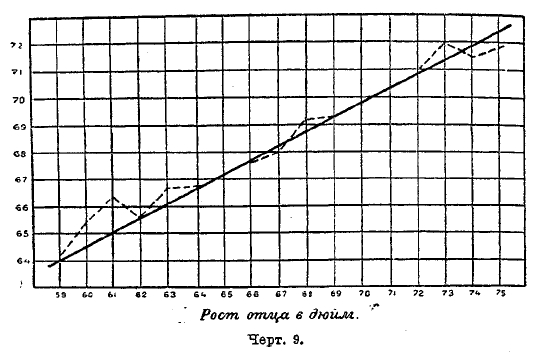
Величину Y — ординату центра х-вого строя, выражаемую формулой (11), можно вычислить, и не прибегая к этой формуле. В самом деле, Y есть ордината центра х-вого строя; для ее нахождения умножаем численность n^у_х одного из прямоугольников х-вого строя на соответствующую ординату у, складываем такие выражения для всех многоугольников х-вого строя и делим сумму на его численность n_х. В результате получится величина Y. Все эти центры строев будут лежать на одной прямой, если распределение строго нормальное и все вычисления, безусловно, точны. Конечно, эти условия на практике никогда вполне не осуществляются; но найденные центры строев составляют ряд точек, расположенных почти на одной прямой. Пример такого расположения центров и соответствующую прямую регрессии можно видеть на черт. 9, заимствованном у Пирсона и выражающем зависимость среднего роста сына от роста отца.

Когда построены центры строев, то можно графически на бумаге провести через центр всего распределения прямую, возможно близко проходящую к центрам строев, и определить тангенс угла наклонения этой прямой к оси х. Найдя этот tg и обозначив буквой ρ₁ представим уравнение (11) в таком виде:

Таким же образом найдем уравнение второй линии регрессии, т. е. (11'), в следующем виде:

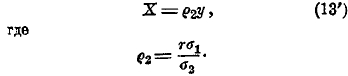
Перемножив величины ρ₁ и ρ₂, находим:

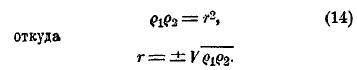
Чтобы определить знак, который надо взять перед корнем, заметим, что σ₁ и σ₂ положительны, а потому r имеет знак, одинаковый с ρ₁ и ρ₂. Величина r есть средняя пропорциональная между ρ₁ и ρ₂: а эти коэффициенты можно найти графически.

Черт. 9.

Так как начало координат находится в центре распределения, то х и у суть уклонения признаков от нормы. В частности, если мы говорим о росте отцов и сыновей, то х обозначает, на сколько дюймов отец выше или ниже нормы; формула (13) показывает, что сын в среднем будет отличаться от нормы на ρ₁х дюймов. Вычисления показывают, что в данном случае ρ₁ = 0,5. Следовательно, в среднем рост сына будет уклоняться от нормы в ту же сторону, как и рост отца, но не на полную величину х, а только на 0,5х. Следовательно, уклонение роста передается по наследству от отца к сыну, но только в половинном размере; природа как бы сглаживает уклонение, стремясь сохранить нормальный образец. Отсюда и произошло название регрессия. Если r положительно, то положительна и ρ₁; с увеличением х увеличивается и Y, как видно из формулы (13); такая корреляция называется положительной. Если же r отрицательно, то с увеличением х величина Y уменьшается. Это — корреляция отрицательная.

Привезенная выше формула (10) распределения по двум признакам может быть обобщена для скольких угодно переменных; это — формула Эджворса. Она позволяет в случае n признаков выразить, среднюю величину одного из них через данные значения остальных n—1. Макдонелль, применяя эту формулу к криминальной антропологии, дал пример реконструирования роста человека по данным размерам некоторых из его костей как то: пальца, локтя, голени и т. д. При этом оказывается, что некоторые кости имеют большее влияние на окончательную формулу, а другие меньшее. Сделанная им проверка полученных результатов на основании опытного материала вполне удовлетворительно подтвердила результаты. Это приводит Пирсона к надежде, что мы теперь приближаемся к осуществлению мысли, высказанной Кювье более 100 лет назад, что со временем ученые будут в состоянии реконструировать все животное по некоторым его костям.

На задачу теории корреляций можно взглянуть и с несколько иной точки зрения. В опытных науках, изучая зависимость изменений одной величины (у) от другой (х), принимаются тщательно предосторожности, чтобы во время производства опытов оставались постоянными все величины, кроме самих х и у. В науках наблюдательных осуществить это требование невозможно: наблюдая, как изменяется у с изменением х, мы заранее знаем, что на у оказывает влияние, кроме х, еще целый ряд других величин, которые нам даже не известны. Не будучи в состоянии установить точную функциональную зависимость у от х, мы можем, однако, интересоваться, в какой мере изменение х отражается на у, т. е. мерой корреляционной зависимости между у и х.

В настоящее время математическая статистика, в особенности теория кривых распределения и корреляций, благодаря школе Пирсона, заведуемому им и основанному ранее Гальтоном Институту евгеники (см.), а также журналу «Биометрика», достигла значительных результатов и стала применяться не только в биологии и общественных науках, но даже в педагогике и экспериментальной психологии.

Литература. Элементарные курсы: Л. К. Лахтин,  «Курс теории вероятностей», 1924; Castelnucvo, «Саlсоlо delle Probabilità» , Vol. J. Bologna. Более полные курсы: А. А. Марков, «Исчисление вероятностей», 1924 (1-е изд.); Р. Lévy «Calcul des probabilities», Paris, 1925. К. Pearson, «Tables for Statisticians» (1914).

Л. Лахтин.