Теплота

Теплота, или тепло (см. XLIII, 315/17), энергия тех совершающихся внутри тел процессов, которые носят т. н. беспорядочный, хаотический характер. Сюда относятся: прежде всего — кинетическая энергия разного рода движений молекул и атомов, но движений, так сказать, индивидуальных, которые различны количественно у разных молекул и атомов и которые у каждой такой частицы меняются со временем случайно, таковы — движение поступательное, движение вращательное, движение колебательное; затем сюда же относится потенциальная энергия молекулярных и атомных сил, поскольку эти силы распределены на отдельные молекулы и атомы беспорядочно, случайно (поэтому, например, энергия тяжести, энергия движения тела, как целого, и т. п. не есть теплота).

Вообще говоря, всякое тело обладает известным запасом тепловой энергии, который при известных условиях может увеличиваться или уменьшаться: мы говорим тогда о назревании или охлаждении тела. Конечно, как энергия, теплота не может исчезнуть, но как энергия данного вида, она может стать в теле меньше или больше или вследствие превращения ее в энергию другого вида (другой формы), или вследствие превращения какой-нибудь иной энергии в теплоту, или же, наконец, вследствие перехода теплоты от данного тела к другому и обратно. Так, например, при быстром расширении или сжатии тел они соответственно охлаждаются или нагреваются, так что количество теплоты в телах становится меньше или больше: в первом случае тепловая энергия переходит в механическую работу, во втором — обратно; точно так же, например, тело, находящееся в воздухе, смотря по обстоятельствам может нагреваться или охлаждаться, например, вследствие того, что оно или получает из воздуха тепловую энергию, или отдает воздуху часть своего запаса этой энергии. Однако, и в том случае, когда наблюдение не обнаруживает изменения количества теплоты в теле, процессы притока и оттока теплоты из тела, а также процессы превращения теплоты в иные виды энергии и иных видов последней в теплоту все же никогда не прекращаются: сохраняется лишь равенство между приращением теплоты в теле и убылью ее за то малое время, в течение которого мы можем сделать заключение о том, меняется ли количество теплоты, или нет. Мы говорим тогда, что рассматриваемое тело находится в тепловом равновесии.

Первое понятие о теплоте мы получаем путем ощущения «тепла» и «холода»; это ощущение показывает нам у тел разные «степени тепла и холода», однако оно нередко нас и обманывает.

Ощущение вообще не дает нам возможности судить ни о количестве теплоты в данном теле, ни о ее концентрации (количестве теплоты в единице массы или единице объема), ни о так называемой температуре (см. ниже).

В основании этого ощущения лежит обмен теплоты между испытуемым телом и нашими органами ощущений. Если теплота к последним притекает, тело нам кажется теплым — и тем более теплым, чем сильнее приток теплоты; в случае обратного перехода теплоты с наших органов ощущений в испытуемое тело — последнее нам представляется холодным, и тем более холодным, чем быстрее идет этот переход теплоты. Аналогичные процессы идут и между всякими телами в природе, как соприкасающимися между собой, так и разделенными между собой при посредстве других тел или даже безвоздушного пространства.

Об изменении количества теплоты в теле можно судить по тем изменениям, которые при этом испытывают размеры тела: это — так называемое тепловое расширение (см.) и сжатие при нагревании или охлаждении. А так как за изменениями размеров любого тела следить неудобно, то применяют для этой цели специально приспособленные тела, изменения размеров которых при нагревании и охлаждении сравнительно велики и легко видимы. Такие тела суть термометры (см.). Приводя термометр в возможно лучшее соприкасание с испытуемым телом, мы по изменению размеров у термометра сейчас же заключаем о направлении движении теплоты: расширение в термометре указывает на приток теплоты от тела к термометру, сжатие — на течение теплоты от термометра к телу, отсутствие изменений размеров — на отсутствие движения теплоты, — на тепловое равновесие обоих тел. Если нет обмена теплоты между телами, мы говорим, что их тепловые состояния одинаковы, и характеризуем тепловое состояние тела его так называемой температурой. Когда тело нагревается, его температура повышается, при охлаждении — она понижается, при тепловом равновесии температура тел не меняется. Мерой температуры может служить расширение любого термометра: получается чисто условная шкала температуры, например, шкала Цельсия по газовому термометру или шкала Реомюра по данному стеклянному термометру с ртутью, спиртом и т. д.; очевидно, что теплота «сама по себе» естественным путем всегда переходит с тела высшей температуры на тело температуры низшей.

До средины XIX в. сущность теплоты была не установлена; большинство ученых считало последнюю некоторым материальным агентом, своего рода материей — не уничтожаемой и не созидаемой. Между тем теплота, как таковая, несомненно создается в процессах трения и во многих других (например, химических), и несомненно в известных случаях исчезает. Однако, опыт показывает всегда в этих случаях параллельное исчезание или появление энергии в каком-либо ином виде. Это и привело к учению о теплоте, как энергии, к так называемой механической теории теплоты, или термодинамике, в основе которой лежит эквивалентность теплоты и энергии.

Дело в том, что для измерения теплоты определенное ее количество принято за единицу и названо калорией (см. XIX, прил. к 603/604, единицы измерения, 5); если же теплота есть вид энергии, то она может быть измерена также в эргах, килограммометрах, джоулях (см. там же), как всякая энергия или как работа. Поэтому, очевидно, одно и то же количество теплоты может быть измерено и некоторым числом калорий и некоторым числом джоулей, и отношение этих чисел  даст: сколько джоулей соответствует одной калории или сколько калорий — одному джоулю. Это — механический эквивалент теплоты и тепловой эквивалент работы — числа, разумеется, не зависящие от того, из какого опыта и, пользуясь какими количествами теплоты или работы мы их определяем. Оказалось, что калория, т. е. количество тепла, нужное для нагревания 1 грамма воды от 14,6° до 15,5°С, эквивалентна энергии J, причем J = 41,85 млн. эргов = 4,186 джоуля = 0,127 килограммометра.

На основании закона сохранения энергии (см.) полная энергия какого-либо тела (или системы) может возрасти только от того, что телу извне сообщена энергия. В чисто механических процессах эта последняя энергия дается работой внешних относительно тела сил; в тепловых процессах изменение полной энергии тел может быть вызвано и сообщением телу теплоты. Таким образом, если телу сообщено достаточно малое (теоретически — бесконечно малое) количество теплоты, которое мы обозначаем ΔQ (в калориях), и если внешние силы совершили бесконечно малую работу ΔW, то всего телу сообщено количество энергии JΔQ + ΔW, и это должно давать бесконечно малое приращение ΔЕ всей «внутренней» энергии тела, так что мы имеем:

это — первый основной закон термодинамики, ведущий к большому ряду очень важных (теоретически и практически) выводов.

Очень малые (теоретически — бесконечно малые) изменения внутренней энергии Е, теплоты Q, работы W удобно брать потому, что для них легко получить сравнительно простые выражения, с которыми можно с удобством производить вычисления.

Если рассматриваемый процесс конечен, то мы его должны разбить на бесконечно малые части — стадии, и изменение энергии за весь процесс представится суммой бесконечно малых изменений ΔЕ. Это сложение мы обозначим знаком ∑. Тогда

очевидно, левая часть этого равенства даст полное изменение внутренней энергии тела за весь процесс, а правая — полную полученную телом теплоты и всю полученную работу. Из нашего соотношения следует: если тело претерпело ряд таких изменений, что в конце концов вернулось к своему начальному состоянию и, стало быть, к начальному значению внутренней энергии, так что ∑ΔE=0 (в этом случае говорят, что тело совершило цикл изменений, выполнило «круговой», или «замкнутый» процесс), то или в результате полученная телом извне теплота (∑ΔQ) превратилась в работу, выполненную телом, или обратно, за счет сообщенной телу работы (∑ΔW) тело отдало соответственное (эквивалентное) количество теплоты наружу. В первом случае тело служит машиной для получения работы за счет теплоты, во втором — для получения теплоты за счет работы. Первый случай дает возможность осуществления так называемых тепловых двигателей (паровые машины, см.; двигатели внутреннего сгорания, см.); второй случай осуществляется в холодильных машинах (см.).

Согласно опыту, количество теплоты, нужное для данного нагревания какого-нибудь однородного тела, пропорционально его массе М. С другой стороны, очевидно, что при бесконёчно малом повышении температуры t° тела (на Δt°) нужное для этого количество теплоты можно принять пропорциональным Δt. Таким образом, обозначая через с коэффициент пропорциональности, можем написать: нужное для нагревания тела массы М на Δt° бесконечно малое количество теплоты ΔQ есть

Здесь с, вообще говоря, для разных температур t различно (т. е. является функцией t) и называется удельной теплотой, или теплоемкостью (см.) вещества. Разумеется, величина с зависит и от вещества и от его агрегатного состояния. Кроме того, с зависит еще и от того, при каких условиях происходит нагревание. Так, тело может нагреваться без изменения своего объема; тогда с = с_v есть удельная теплота при постоянном объеме; но тело может нагреваться и с изменением объема, находясь, однако, все время под одним и тем же давлением (например, атмосферным): с будет тогда удельная теплота при постоянном давлении (с = с_р); возможны и иные случаи нагревания; каждому из них будет соответствовать свое особое с, которое вообще зависит, кроме t, еще и от объема (v) тела.

У так называемых идеальных газов (см. ХII, 306), к которым по своим свойствам при известных условиях давления и температуры близки такие газы, как, например, воздух, азот, кислород, водород и др., между молекулами нет действующих сил. Такие силы проявляются лишь при взаимных столкновениях молекул, влекущих за собой изменение движения их. Вся теплоты, содержащаяся в таком газе, или его внутренняя энергия (Е), слагается, стало быть, из энергий отдельных, независимых между собой молекул. Значит, величина Е для идеального газа не зависит от того, близки молекулы или далеки одна от другой (в среднем), т. е., иначе говоря, Е не зависит от видимого объема газа (v), а только от температуры (t) его. В случае нагревания идеального газа при постоянном объеме

(потому что тогда работа не совершается, ΔW=0); внутренняя энергия идеального газа будет

где вообще с_v для разных t различно, чем и обусловлена необходимость рассматривать малые нагревания Δt, при которых с_v можно считать не меняющейся. Но уравнение состояния идеального газа (см. XII, 313) показывает, что при неизменном объеме давление, оказываемое газом на стенки сосуда или на всякую площадку внутри газа, меняется с t, убывая при понижении с_v. Таким образом, при известной температуре t₀ давление газа станет, очевидно, нулем, т. е. исчезнет вовсе; это будет иметь место при условии

Эта температура называется «абсолютным нулем», ибо ниже ее температуры не может быть (р не может стать отрицательным). Соответственно этому Т = t + 273, т. е. температура, считаемая в градусах Цельсия от абсолютного нуля, называется «абсолютной температурой» (см.). Очевидно, изменение T на ΔT равно изменению t на Δt, т. е. мы можем написать для идеального газа

Опыты показали, что у газов, близких к идеальным, в известных, не слишком широких пределах температуры, с_v и c_р почти не меняются с изменением t. Если бы с_v оставалось неизменным вплоть до —273°С, то было бы для идеального газа

С другой стороны, мы можем нагревать идеальный газ при постоянном давлении, причем его температура опять-таки повышается на ΔT. На это потребуется количество энергии

при этом газ будет расширяться, совершать работу, преодолевая внешнее на него давление р. А так как между молекулами нашего газа, по условию, никаких сил нет, то разность количеств энергии, потребных для нагревания в обоих рассмотренных случаях, или JM(с_р — с_v) ΔТ, обусловлена лишь совершенной газом работой, которую легко вычислить. Именно, на очень малую площадку поверхности газа ΔS (которую по ее малости можно считать плоской) действует нормальное давление р (т. е. сила на каждый квадратный сантиметр); значит, на площадку ΔS действует сила pΔS, и вся поверхность газа растягивается, так что всякая площадка ΔS перемещается параллельно себе на малое расстояние h. Работа газа измеряется, как и всякая работа, произведением силы (pΔS) на произведенное ею по своему направлению перемещение (h); в данном случае работа будет равна

здесь ΔSh есть приращение объема газа в данном месте. Стало быть, для поверхности S газа работа будет (р везде одно и то же)

где Δv есть приращение начального объема v газа. Итак, мы имеем, как выражение закона сохранения энергии,

из этого-то соотношения и было впервые вычислено J (способ Майера, 1842, см. XXVII, 628). Но из уравнения состояния pv = RT вытекает для случая нагревания при постоянном давлении: р (v + Δv) = R (T + ΔТ), следовательно

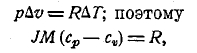
так что R получает простое физическое значение; в то же время оказывается

В кинетической теории газов (см. газы.) получается для идеального газа

где (Е_k) есть энергия поступательного движения молекул, и мы поэтому имеем для нее выражение:

в то время как для всей энергии

Деление этих уравнений друг на друга дает

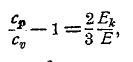
т. е. отношение с_р/c_v определяется через отношение кинетической энергии поступательного движения молекул ко всей энергии идеального газа. Очевидно, наибольшее возможное значение E_k/E g есть 1, когда вся энергия газа заключается в поступательном движении его молекул. Тогда будет

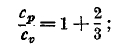
это так и есть у газов одноатомных (аргон, гелий и другие благородные газы; ртутные пары). Стало быть, у этих газов нет в молекулах ни вращения, ни колебательного движения.

Кинетическую энергию поступательного движения молекул газа можно записать и так (m — масса молекулы, u — ее скорость):

где ½ mω² есть средняя кинетическая энергия одной молекулы, а N — число молекул. Тогда

средняя энергия молекулы оказывается пропорциональной абсолютной температуре Т, так что можем взять

Мы видим отсюда, что при температуре абсолютного нуля (Т=0) не может быть поступательного движения молекул газа, ω = 0. Для другого газа при той же Т будем иметь иные m, N, R, ω, и значит будет

Смешаем эти два газа между собой. Опыт показывает, что в таком случае и смесь остается при той же температуре Т. Если бы ψ и ψ₁ были различны, молекулы наших двух газов при столкновениях между ними меняли бы свои кинетические энергии, и у смеси не могло бы быть той же неизменной Т. Следовательно, как это заключил еще Максвелл, должно быть ψ = ψ₁ т. е. ψ одно и то же для всех газов. Таким образом, формула ½ mω² = ½ m₁ω₁² =…= ψT является механическим определением температуры; ψ есть «универсальная» постоянная.

Так как для двух газов

и при одинаковых р, v, Т имеем

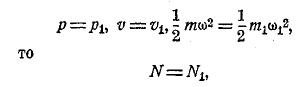
т. е. числа молекул одинаковы у обоих газов. Это — закон Авогадро, найденный последним из химических соображений. Отсюда следствие: при одинаковых р, Т в одном куб. сантиметре разные газы имеют одно и то же число молекул N.

В одном грамме их будет N/d, если d — масса газа в 1 куб. см, т. е. плотность газа. Следовательно, М граммов газа будут содержать при данных р, Т число молекул

Пусть теперь М есть масса грамм-молекулы (см. газы, XII, 313). Тогда, как известно, M/d есть число, одинаковое для всех газов. Следовательно, если брать   всегда грамм-молекулу газов, мы получим и R всегда одно и то же. А так как R есть число молекул вещества в М гр., то очевидно оно не меняется (при данном М), как бы ни менялось состояние вещества; итак, R оказывается также универсальною постоянною для всех тел во всех их состояниях (твердом, жидком, газообразном).

Благодаря этому для грамм-молекулы газа

и наш закон получает тоже универсальный характер. При этом оказывается для всех газов одним и тем же количество

Действительно, опыт показывает, что для всех газов М (с_р — с_v) = круглым счетом 2 калориям. Есть возможность разными способами найти R, а значит и ψ. Оказывается, R = 6,06·10²³; ψ = 1,37·10^-16. Так как c_p/c_v = 5/3 для всех одноатомных газов, то мы получаем для них

что и согласно с опытом в широких пределах температуры.

Те же соображения, согласно которым у двух газов одной Т должно быть

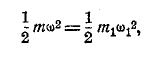
приводят и к заключению, что при тепловом равновесии газа и средняя энергия вращательного движения и средняя энергия колебательного движения должны быть с средней энергией поступательного движения в определенных отношениях. В самом деле, скорость ω можно разложить на три слагающие по трем взаимно перпендикулярным направлениям и, так как давление газа по любому направлению одно и то же, то и энергии поступательного движения по этим трем направлениям должны быть равны между собой и давать величину 1/3 E_k, или 1/6 mω² для всякого направления. Мы здесь имеем как бы 3 вида энергии, и вся энергия распределена по этим видам равномерно. Эти виды называются степенями свободы. Если есть у молекулы вращение около оси, оно соответствует новому виду энергии, новой степени свободы. У двухатомных молекул, которые имеют форму тел вращения около оси, вращение около этой оси симметрии невозможно, но возможно вращение около других двух направлений, перпендикулярных к оси симметрии и друг к другу. В этом случае мы имеем, кроме трех видов энергии поступательного движения, еще два вида энергии вращения. А так как, по сказанному, энергия Е распределена по степеням свободы равномерно, то в данном случае, очевидно,

что и имеет место у таких газов, как, например, H₂, O₂, N₂ и т. д. Отсюда следует для двухатомных газов

что приблизительно согласуется с опытом.

Все эти выводы весьма общего и часто универсального характера являются подтверждением кинетического представления о природе теплоты.

То же дают и свойства других тел. Именно, у твердых тел молено принять молекулярное движение только в виде колебаний атомов внутри молекул; всякое колебание по одному направлению имеет энергию двух видов — кинетическую и потенциальную. Следовательно, если атомы могут колебаться по любому направлению, или (что сводится к тому же) по трем взаимно перпендикулярным направлениям, то каждый атом имеет 6 степеней свободы, и каждая молекула 6n степеней свободы, если в молекуле n атомов (одинаковых или различных — это все равно). Но для грамм-молекулы вещества при температуре T на 3 степени свободы (одноатомный газ) приходится 3 Т кал. тепловой энергии; значит, на 6 л степеней свободы при температуре Т придется энергии 6nТ, т. е. мы имеем

предполагая, конечно, что и в рассматриваемом случае с_v не меняется с Т.

Здесь M/n = А есть средний атомный вес твердого тела, так что

для всех твердых тел. Для химических элементов подобный закон нашли эмпирически Дюлонг и Пти (1819), а для соединений — Нейманн и Копп (1831—1864).

Опыт дает (для Ас_p) числа около 6,5 с резкими уклонениями у некоторых веществ. У жидкостей Ас_v вообще гораздо более 6, что объясняется наличностью энергии других видов (поступательного и вращательного движения). Возникает вопрос о причине уклонений Ас_v от числа 6, и ответ на это дан опытом давно: с_v и с_р переменны с t. Закон поэтому имеет силу лишь в определенных границах t. Точно так же и у газов с_v переменно с t (довольно слабо при высоких t и очень сильно при низких, когда, например у водорода, Мс_v вместо 5 имеет значение всего 3).

Эти явления подвергнуты опытному и теоретическому исследованию лишь в недавнее время, когда были выработаны способы определять удельные теплоты при вполне известных температурах, т. е. по формуле, например,

при достаточно малых Δt. Ранее нагревание производилось в широких пределах изменения t (например, от t₁ до t₂), так что было

и удельной теплоты находили как некоторую среднюю величину между t₁ и t₂, по формуле

С другой стороны, явление стало доступно опыту лишь в недавнее время еще и потому, что значительное уменьшение с_v с температурой наблюдается лишь при очень низких t, а последние стало возможным легко осуществить лишь после открытия способов сжижения в больших количествах воздуха и других трудно сжижаемых газов. (О сжижении газов см. холодильные машины, XLV, ч. 2, 671 сл.).

В следующих таблицах показана зависимость Мс_v от Т для водорода и зависимость Ас_v и Мс_v от Т для двух твердых веществ (свинец, плавиковый шпат). Чертеж дает для плавикового шпата зависимость Ас_v от теплоты

Как видим, изменение Мс_v и Ас_v с температурой очень велико. По ходу кривой ясно, что у твердых тел с_v стремится к нулю при Т = 0¹⁾. Вышеупомянутые законы, таким образом, имеют силу лишь при достаточно высоких температурах, и у твердых тел это, так сказать, предельные законы; теоретической величины для Ас_v не получается для свинца и при 3°С, хотя здесь 5,84 и близко к 6. У плавикового шпата при 45°С Ас_v имеет еще значение 5,45 (это вещество имеет в молекуле 3 атома, и для него М = 78,1).

Это свойство удельных теплот  имеет очень большое значение. Дело в том, что исходя из основного предположения кинетической теории вещества, что энергия отдельных молекул может иметь всевозможные значения в пределах 0 и бесконечности, мы неизбежно приходим к равномерному распределению энергии по разным степеням свободы. А отсюда в свою очередь следует, что  с_v, заметно не меняется с температурой. Таким образом, изменяемость  с_v с температурой указывает на то, что распределение энергии по степеням свободы неравномерно при низких t даже и у идеальных газов. Согласно современным воззрениям, это возможно лишь при условии, что энергия молекул не может иметь любых значений, а должна всегда быть кратным числом некоторого минимального количества энергии, некоторой «порции», или как бы «атома» энергии, получившего название кванта.

¹⁾ Многие ученые предполагают, что такое приближение  с_v к нулю имеет место и у газов («вырождение» газов). Но это явление должно сказаться лишь при самых низких температурах.

Так же получается объяснение изменяемости  с_v и у двухатомных газов и у твердых тел. В последнем случае оказывается (теория Дебая), что при очень низких температурах Е пропорционально Т, а с_v стало быть, пропорционально Т³, что и согласно с наблюдениями. Вопрос этот тесно связан с объяснением явлений лучеиспускания т. н. черного тела (см. излучение, XXI, 474 и след.), и кванты вошли в науку впервые именно в теории этого лучеиспускания (Планк, 1906).

Молекулы, как и атомы, состоят из положительно заряженных «ядер» и отрицательно заряженных «электронов» (см.); все электроны одинаковы между собой; масса электрона в 1 800 раз меньше, чем масса ядра легчайшего атома — водородного. Не только атомы (или их ядра) могут колебаться в молекуле, подобные движения могут иметь и электроны. Их энергия, стало быть, тоже входит в состав полной энергии тела, в состав его «теплоты» И ядра и электроны приходят в колебание при столкновениях молекул, а такое движение порождает в окружающем пространстве электромагнитные волны, которые мы называем светом (видимым или невидимым, см. свет, XXXVII, 562/65). Эти волны расходятся во все стороны, их энергия из рассматриваемого тела уходит. Это и есть процесс излучения, или лучеиспускания, идущий, очевидно, при всякой температуре. Благодаря этому процессу, тепловая энергия тел будет уменьшаться, температура — понижаться, тело будет охлаждаться. Наоборот, если электромагнитные волны попадают на молекулы тела, они могут вызвать колебания внутри молекул, которые в свою очередь изменят и энергию поступательного движения, так что энергия тела станет больше. Тело нагреется: температура его станет выше. Мы имеем процесс поглощения энергии. Из сказанного ясно, что между молекулами в эфире есть всегда энергия волн (лучистая энергия), которая тоже входит в состав того, что мы называем теплотой в теле, ибо она распределена на колебания разных периодов тоже хаотически, беспорядочно. Только при невысоких температурах эта часть энергии ничтожна.

Лучеиспускание и лучепоглощение — не единственный процесс, которым происходит обмен теплоты между телами. Другим процессом этого рода является теплопроводность. Механизм этого явления в общем сводится к тому, что молекулы с большей средней кинетической энергией при столкновении с молекулами меньшей кинетической энергии выравнивают свои энергии, большая — уменьшается, меньшая — увеличивается. А так как большая энергия соответствует телу с высшей температурой, то в результате это тело охлаждается, а другое — нагревается, и процесс идет от границы соприкасания обоих тел в обе стороны. Это и есть явление теплопроводности. Кинетическая теория газов позволяет войти во все детали механизма этого процесса и вычислить так называемый коэффициент теплопроводности (см. теплопроводность) газов. Получается хорошее согласие с опытом.

Если два тела А и В одной температуры соприкасаются друг с другом по некоторой плоскости, и если тело А, как целое, имеет относительно тела В скорость поступательного движения v параллельно плоскости соприкасания, то молекулы тела А, кроме беспорядочного «теплового» движения, имеют все одинаковую и по одному направлению скорость v. Эти молекулы будут отчасти проникать внутрь тела В, а молекулы тела В внутрь тела А; кроме того, будут происходить столкновения молекул обоих тел между собой; так. образом, молекулы тела А будут сообщать молекулам тела В скорость по направлению своего поступательного движения. В результате этого взаимодействия движение тела А со скоростью v замедлится, а тело В придет само в движение потому же направлению, по которому движется А. Это взаимодействие двух тел носит название явления трения, в данном случае внешнего (внутреннее трение имеет место, если разница скорости v существует между слоями одного и того же тела). И этому явлению кинетическая теория газов дает полное и согласное с опытом механическое объяснение. Если тело В, как целое, в движение придти не может, то приобретенная его молекулами лишняя скорость при столкновениях распределится беспорядочно между его молекулами, и в результате средняя кинетическая энергия поступательного движения молекул тела В сначала вблизи границы двух тел, а потом и далее внутри В станет больше начальной. Это значит, что у тела В происходит повышение температуры, передающееся, конечно, и телу А. В результате трения оба тела нагреваются; мы имеем создание тепловой энергии. Трение проявляется как сила, противодействующая движению тела А. Если, несмотря на действие этой силы, тело А движется равномерно со скоростью v, т. е. как бы по инерции, — это значит, что извне к телу А приложена сила, уравновешивающая силу трения. Непрерывная работа этой силы есть механическая энергия, затрачиваемая при движении: она-то и проявляется в явлении трения как теплоты, эквивалентная затраченной работе. Измерение обеих величин дает возможность найти механический эквивалент теплоты, который был впервые определен по этому методу Джоулем (1847).

Трение есть один из примеров превращения механической энергии в теплоту; другой подобный пример мы имеем при сжатии идеального газа, где в теплоту превращается работа сжатия, видимого уменьшения объема. У тел всякого типа в подобном случае в теплоту превращается — сверх работы видимого сжатия — и часть энергии, обусловленной внутренними притягательными силами между молекулами. Поэтому и наоборот, если, например, неидеальный газ нагревается при постоянном давлении, то сообщаемая газу теплота тратится частично и на преодоление сил молекулярного притяжения. Ясно также, что если идеальный газ расширяется в пустоту, следовательно, никакого внешнего давления не преодолевает, то он охлаждаться не должен, а наблюдаемое в таком случае охлаждение действительных газов имеет своей причиной проявление молекулярных сил и может служить их мерой.

В разбираемых случаях создание и исчезание теплоты не всегда может быть замечено. Именно, если процесс сжатия или расширения идет достаточно медленно и если тела, с которыми мы экспериментируем, не изолированы от других тел (например, воздуха), то появляющаяся в теле теплота может утекать наружу, а исчезающая пополняться притоком извне, так что температура тела может нам представиться неизменяющейся. Мы имеем тогда т. н. изотермический процесс. Если же мы  поставим наше тело в такие условия, что обмен тепла между ним и иными телами исключен (приблизительно  это осуществится, если процесс в теле протекает достаточно быстро, так что для притока или оттока теплоты не будет времени), — мы будем иметь процесс, называемый адиабатным, и при нем нагревание и охлаждение тела будет заметно.

При известных внешних условиях всякое вещество, вообще говоря, представляется нам в одном из трех, по-видимому, совершенно непохожих одно на другое, агрегатных состояний, твердом, жидком, газообразном. Различие между этими состояниями, в общем, сводится главным образом к различию в среднем расстоянии между молекулами и в величине междумолекулярных сил. Отвлекаясь от явлений изменения молекулярного строения (так называемые процессы ассоциации и диссоциации), можно сказать, что при переходе тел из твердого состояния в жидкое и затем в газообразное, среднее расстояние между молекулами увеличивается, а молекулярные силы ослабевают. Отсюда ясно, что эти процессы (плавление и  испарение) не могут идти без затраты на них энергии. Однако, в частных случаях эти процессы могут иногда протекать так быстро, что извне энергия поступать не успевает: тогда на процесс тратится энергия самого же тела, т. е. его собственная теплота, так что тело при этом охлаждается. Так охлаждается жидкость при быстром своем испарении и может при этом даже затвердеть. Вообще же говоря, подобные процессы идут сравнительно медленно, и тогда они протекают изотермически, за счет теплоты, доставляемой телу извне. Соответственно старым взглядам на теплоту, как на вещество, не уничтожаемое и не создаваемое, количество теплоты, нужное для плавления или испарения, но не обнаруживаемое термометром, получило название скрытой теплоты плавления или испарения. При обратном процессе затвердевания или сжижения эта скрытая теплота выделяется назад.

Однако, термин «скрытая теплота» не соответствует современному представлению о теплоте как об энергии хаотических молекулярных процессов. Именно, теплота, взятая из нагревателя для плавления или испарения, не остается в теле, как теплота; она превращается там в работу, а не просто «скрывается». Точно так же при процессах затвердевания и сжижения теплота не появляется из скрытого состояния, а создается вновь из механической работы.

Механическое представление о теплоте, приведшее к учению об эквивалентности теплоты и энергии, включило тепловые явления в разряд процессов, подчиненных закону сохранения энергии. Однако, этот закон носит чисто ограничительный характер, указывая лишь, чего в природе не должно быть (исчезания или создания энергии), но ничего не говорит о том, в каком направлении должны протекать физические явления. Между тем внимательное изучение этих явлений обнаружило в них стремление протекать в определенных направлениях. Именно, так протекают в природе процессы, называемые самопроизвольными, т. е. идущими сами по себе, без воздействия извне. Сюда относятся, например, диффузия (см.), переход теплоты от горячих тел к холодным, многие химические реакции. В этих процессах энергия не теряется и не приобретается, но может лишь менять свой вид, свою форму. Однако, данное количество энергии для нас не всегда одинаково в смысле пользы, в смысле ценности, потому что мы не при всех условиях можем использовать его для получения механической работы. Это обстоятельство стоит в связи с тем, что все процессы в природе, строго говоря, необратимы, т. е. не могут быть по нашему произволу выполнены и в одном и в противоположном направлениях — при прочих равных условиях.

Пусть мы, например, быстро сжимаем газ и тем его нагреваем; очевидно, расширяя газ в тех же пределах, мы его охладим, и, по-видимому, этот процесс обратим. Однако, на самом деле это один из процессов лишь почти обратимых, ибо, как бы мы ни осуществляли такое расширение и сжатие газа, будет при этом стираться и нагреваться поршень и т. п. Энергия, затраченная на сжатие, не восстановится целиком при расширении газа: ее часть, хотя и малая, уйдет для нас непроизводительно, мы ее собрать не можем, она затрачена, рассеяна, хотя закон сохранения энергии и не нарушен. Чем менее это рассеяние энергии, тем совершеннее обратимость процесса, и с этой точки зрения смешение горячей воды с холодной есть пример совершенно необратимого процесса. Из полученной смеси воды некоторой средней температуры мы не можем получить прежней горячей воды без затраты работы. Здесь энергия рассеялась, обесценилась для нас потому, что теплота высокой температуры превратилась в теплоту низкой.

1 000 малых калорий при 100°С и 1 000 малых калорий при 0°С, это — все те же 427 килограммометров энергии; первый закон термодинамики не делает никакого различия между этими количествами теплоты Однако, теплота при 100°С и при 0°С — не одно и то же, и в установлении этого положения заключается второй закон термодинамики. Именно, два равные количества теплоты неодинаковой температуры не равноценны для получения из них механической работы. В самом деле, превращение теплоты в работу осуществляется при помощи тепловых двигателей. В этих машинах теплота, заставляя расширяться пар или газ, приводит в движение поршень, а это движение затем утилизируется. Так как пар или газ должен быть нагрет, то, очевидно, надо иметь тот или иной источник тепла («нагреватель»), из которого берется количество теплоты Q. Но для непрерывной работы машина должна, совершив ряд изменений своих состояний, периодически возвращаться в начальное состояние, т. е. должна выполнять известный цикл изменений (см. цикл Карно). Значит, если в определенной стадии работы машины вещество нагревается, получая количество тепла Q, то непременно должна быть и такая стадия цикла, когда вещество охлаждается. Является необходимость иметь «холодильник» (резервуар тепла более низкой температуры, чем нагреватель), куда вещество отдает некоторое количество теплоты q.

Таким образом, в работу может превращаться только разность, так что превратить Q целиком в работу Q—q нельзя; доля этого количества, равная q, остается в форме теплоты, только изменив свою температуру на более низкую.

В этом «падении теплоты» с высокой температуры на низкую в свое время видели (Н. Л. Карно, 1824) причину превращения тепла в работу, подобно тому, как падение массы воды с высокого уровня на низкий является причиной получения работы. Однако, эта аналогия не верна, и причина получения работы вовсе не в падении теплоты, хотя это падение есть неизбежное условие для получения работы.

Возможен и обратный процесс: возможно превратить теплоту низкой температуры в теплоту высокой, однако это осуществимо только при условии затраты работы или при условии какой-нибудь иной «компенсации». В этом и состоит второй закон, или принцип, термодинамики, который часто формулируется так: «теплота не может сама по себе переходить с низкой температуры на высокую» (Клаузиус, 1850), — где «сама по себе» значит без затраты, например, работы или вообще без какого-либо остающегося изменения в системе, компенсирующего переход теплоты. Иначе можно сказать: «Имея систему тел разной температуры, нельзя получить механическую работу путем охлаждения системы до температуры, более низкой, чем температура самого холодного из тел» (Кельвин, 1851), т. е., например, нельзя пользоваться для получения механической работы теплотой океана, воздуха и т. п. Но ведь это и значит как раз, что для целей получения работы теплота для нас тем мало ценнее, чем ниже ее температура. Итак, понижением температуры теплота обесценивается. Но один из преобладающих самопроизвольных процессов в природе, это — превращение энергии разных видов в тепло и переход последнего с теплых тел на холодные. Следовательно, все самопроизвольные процессы в природе имеют такое направление, что энергия обесценивается, рассеивается. Поэтому, второй закон термодинамики называют законом рассеяния энергии.

Из второго закона термодинамики вытекает такое следствие. Некоторая система проходит обратимым процессом через ряд состояний, в течение которых она имеет абсолютные температуры Т₁, Т₂, Т₃..., и в это время получает количества теплоты (очень малые) Δq₁, Δq₂, Δq₃... Тогда сумма Δq₁/T₁ + Δq₂/T₂ + Δq₃/T₃ +… = ∑q/T зависит лишь от начального и конечного состояний нашей системы и вовсе не зависит от того пути или способа, по которому совершается переход между крайними состояниями. Если некоторое определенное состояние нашей системы мы примем за «нормальное», то значение вышеприведенной суммы при переходе системы из данного состояния в это нормальное состояние Клаузиус назвал энтропией системы в данном состоянии. Оказывается, что для всякого замкнутого процесса энтропия, подобно энергии, имеет в конце процесса то же самое значение, какое было в начале; в процессах же необратимых энтропия возрастает, и тем сильнее, чем более процесс уклоняется от обратимости. Поэтому приращение энтропии может быть принято за меру необратимости процесса; а так как чем более необратимость, тем сильнее рассеивается, обесценивается энергия, то энтропия и является мерой этого рассеяния, обесценивания.

Планк (1909) назвал энтропию мерой «предпочтения», «пристрастия» природы к тому или иному процессу. В самом деле, если система переходит сама по себе из состояния А в состояние В, значит этот процесс предпочитается природой, к нему последняя имеет как бы пристрастие, и процесс необратим. Если он обратим, природа к нему равнодушна. Но все процессы в природе необратимы; все они, в конце концов, сводятся к тому, что механическая энергия разных видов и форм сама по себе превращается в теплоту, а последняя перетекает с теплых тел на холодные: стало быть, энтропия системы — в данном случае вселенной — непрерывно возрастает. Энергия вселенной, не меняясь с течением времени, сама по себе все более и более обесценивается, рассеивается, и вселенная стремится превратить всю свою энергию в теплоту общей температуры, идя, таким образом, к смерти, к кончине мира. Однако, вышеприведенные редакции второго закона термодинамики сообщают ему своеобразный характер, которого не имеет, например, первый закон. Именно, мы не можем без соблюдения известных условий перевести теплоту с более холодного тела на менее холодное, а, стало быть, не можем сделать так, чтобы, например, изменить распределение температуры в газе, нагревая одну его часть на счет другой.

Но представим себе с Максвеллом газ в сосуде, не могущем ни получить  теплоту извне, ни терять его наружу. При таких условиях температура газа меняться со временем не может. Но пусть в сосуде имеется разделяющая его на две части перегородка с маленьким отверстием, через которое может пролететь молекула, и тут это отверстие закрывается форточкой со стеклом. Максвелл воображает себе, далее, микроскопическое существо, одаренное нашей психикой и способное видеть молекулы и манипулировать с форточкой, закрывая и открывая ультрамикроскопическое отверстие перегородки. И вот это существо, «демон», как его назвал Максвелл, видит, как к форточке подлетает молекула с малой скоростью, ударяется о форточку и улетает назад. Но подлетает молекула с большой скоростью: демон открывает для нее форточку и выпускает молекулу на другую сторону перегородки. Для оперирующего таким образом «демона» является, очевидно, возможным в конце концов собрать на одну сторону перегородки все быстрые молекулы газа, по другую — все медленные, т. е. перевести тепло из одной части тела одной температуры на другую, т. е. несомненно нарушить второй закон термодинамики, так как этот перенос произошел без затраты работы и без всякого компенсирующего переход процесса. Работа открытия и закрытия форточки здесь, разумеется, в счет не идет, ибо она может быть мыслима как угодно малой. Таким образом, для нас второй закон есть закон, для демона Максвелла — нет. Однако, этот антропоморфный характер второго закона можно устранить (Больцман, 1877). Дело в том, что теплота есть хаотическое молекулярное явление; хаос управляется законами случайных явлений; эти законы выводятся из теории вероятностей. Второй закон принадлежит к законам, управляющим хаотическими явлениями; следовательно, он есть некоторая теорема теории вероятностей. Эта последняя должна давать и выражение для энтропии. Действительно, все самопроизвольные процессы в природе, идущие, так сказать, по симпатии природы, являются процессами перехода систем: от состояний менее вероятных к состояниям более вероятным. Поэтому энтропия, по Больцману, есть мера вероятности состояния системы, и, например, энтропия идеального одноатомного газа в состоянии теплового равновесия есть мера вероятности стационарного распределения скорости движения между атомами газа. Как определяется эта вероятность и как через нее выражается энтропия, см. энтропия.

В явлениях природы мы имеем, вообще говоря, всегда дело лишь с изменениями энергии и энтропии системы между некоторыми состояниями 1 и 2, т. е. с изменениями энергии  Е₂-Е₁  и с изменениями энтропии S₂-S₁. Поэтому могло бы казаться, что абсолютные значения энергии и энтропии недоступны наблюдению вовсе. Однако, это не так. До некоторой степени есть возможность дать и абсолютные значения Е и S. Особенно это важно по отношению к энтропии, так как, имея возможность знать полное значение ее, мы оказываемся в силах подвергнуть численной проверке целый ряд самых разнообразных физических и физико-химических процессов. Это — одно из сравнительно новых завоеваний термодинамики, основанное на так называемой тепловой теореме Нернста. В формулировке Планка эта теорема гласит: при температуре абсолютного нуля энтропия всякого химически однородного твердого или жидкого тела есть нуль. Таким образом, если тело при постоянном давлении р имеет температуру Т, то его энтропия дается формулой

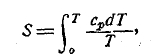
ведущей к двум важным и согласным с опытом заключениям. Так как энтропия не может быть бесконечно велика, то при Т=0 должно быть с_р = 0 (как мы видели выше, для с_v = 0); это — первое следствие. А  второе следствие состоит в том, что по мере приближения температуры тела к абсолютному нулю, коэффициент расширения тела стремится к 0.

Основанная на двух добытых из опыта положениях (1-ый и 2-ой законы), термодинамика в классической своей форме развивалась совершенно независимо от молекулярно-кинетических представлений. Это дало даже повод одно время зародиться научному течению, прямо враждебному атомистике. Однако, успехи современного знания опровергли эту точку зрения, и термодинамика нашего времени, включив в себя и такие явления, как излучение волн, оказывается неразрывно связанной как раз с атомистическими представлениями — не только в вопросе о строении вещества, но в известных случаях и в вопросе о строении самой энергии.

Литература: Хвольсон, «Курс физики», том ІII; Планк, «Термодинамика»; Брандт, Основания термодинамики»; Блох, «Кинетическая теория газов»; Бачинский, «Введение в кинетическую теорию газов».

Д. Гольдгаммер.