Термохимия

Термохимия, отдел химии, посвященный изучению тепловых явлений, происходящих при химических реакциях. Начало термохимических исследований было положено Лавуазье и Лапласом. Расширяя все более и более свои исследования над явлением горения тел и дыхания животных, Лавуазье задался целью измерить количество теплоты, выделяемой при различных химических явлениях и главным образом при явлении горения тел. Тесную связь между тепловыми и химическими явлениями подметила еще теория флогистона (см. XLV, ч. 2, 296), основывавшаяся на том, что в химических реакциях, особенно при сгорании и окислении тел, нечто выделяется и уходит из тела, и это неуловимое нечто представляет собой теплород, — ту невесомую жидкость, которая проникает все тела и от количества которой зависит их различное состояние: твердое, жидкое и газообразное. Количество этой невесомой жидкости, выделяющейся при горении тел, и задумал измерить Лавуазье. При помощи своего ледяного калориметра (см. калориметрия) Лавуазье и Лаплас определяли теплоемкость твердых и жидких тел, теплоту реакции смешения двух жидкостей, — например, теплоту соединения серной кислоты с водой, — и в особенности теплоту горения тел. Они нашли, что 1 грамм древесного угля выделяет при сгорании 7 624 калории (число ниже истинного — 8 137 кал.). Лавуазье и Лаплас определили также теплоту сгорания фосфора, масла, свечи и т. п. тел. Они определяли даже количество животной теплоты, выделяемой морской свинкой. В своем «Мемуаре о теплоте» (1780) они установили первый основной принцип термохимии. Указав на различие между свободной теплотой (chaleur libre) и скрытой (ch. latente), они говорят: «Если при образовании какого-либо соединения или же при изменении состояния тела происходит уменьшение свободной теплоты, то эта теплота восстановится вся целиком, когда тела вернутся к первоначальному состоянию; и обратно, если при образовании какого-либо соединения или перемене состояния тела происходит увеличение свободной теплоты, то новое количество теплоты выделится при обратном переходе тел в первоначальное состояние». Этот вывод они формулируют далее в более общем виде: «Всякие изменения теплоты, которые испытывает система тел при переходе из одного состояния в другое, совершаются в обратном порядке, когда система возвращается в свое первоначальное состояние». В настоящее время мы знаем, что этот основной закон химии является логическим следствием закона сохранения энергии.

После Лавуазье термохимическими исследованиями занимались Румфорд, Дэви, Дальтон, Дюлонг и Депре, но их исследования ограничивались отдельными измерениями теплот сгорания различных тел (главным образом угля и различного рода топлива) в кислороде. Значительный шаг вперед был сделан Г. Гессом, установившим в 1840 г. закон постоянства сумм тепла (Beständigkeit der Wärmesummeu), по которому количество тепла, выделяющегося (или поглощающегося) при химических процессах, зависит только от начального и конечного состояния системы тел, участвовавших в этих процессах. Закон постоянства сумм тепла, открытый Гессом до установления закона сохранения энергии (одним из частных случаев коего он является), казался Гессу настолько очевидным, что он его считал почти аксиомой. Основанием такого взгляда служило, между прочим, и то представление, по которому теплота считалась им жидкостью невесомой, неуничтожаемой и нетворимой ни при каком явлении природы. Руководясь таким взглядом, а также установленным им законом, Гесс утверждал (в противоположность господствовавшему в то время мнению), что при сгорании сложного тела выделяется меньше тепла, чем при горении элементов, входящих в его состав.

В 1852—1853 г. Фавр и Зильберман усовершенствовали метод калориметрических исследований и изучили в термохимическом отношении множество разнообразных реакций. Они ввели новые понятия: (например, тепловой эквивалент и др.), указали  на зависимость свойств тел от количества выделяемого тепла при их образовании (ими было установлено положение: наиболее стойким является такое соединение, образование которого сопровождается наибольшим выделением тепла) и т. д.

Ю. Томсен был первый термохимик, применивший закон сохранения энергии к химическим явлениям. Свою первую статью (1853) он начинает положением: «Напряжение (интенсивность) химической силы в одном и том же теле при неизменной температуре есть величина постоянная». Ю. Томсен, подобно Роб. Мейеру и Г. Гельмгольцу, употреблял тогда слово «Kraft» (сила) там, где в настоящее время мы говорим: «энергия», а поэтому, согласно теперешней терминологии, мы можем перевести положение Ю. Томсена так: запас химической энергии тела при неизменной температуре есть величина постоянная. Если напряжение химических сил (запас химической энергии) в теле при каких-либо условиях уменьшится, так что тело превратится в другое, отличное от первого в термохимическом отношении, то выделится большее или меньшее количество работы. Эта работа может быть измерена в виде тепла, выделяющегося при этом процессе: все количество тепла, выделившегося при химическом процессе, может служить мерой силы (работы), совершенной в этом процессе.

Количество тепла, эквивалентное всему запасу химической энергии тела (Intensität der chemisehen Kraft), Ю. Томсен назвал термодинамическим эквивалентом тела (thermodynames Aequivalent); тела с одинаковыми термодинамическими эквивалентами он назвал изодинамическими (isodyname), с неравными – гетеродинамичесими. Для одного и того же тела термодинамический эквивалент всегда один и тот же, для изомерных тел – он различен. Алгебраическую сумму количеств тепла, выделяющихся при химической реакции, Ю. Томсен предложил назвать тепловым эффектом (Wärmetonung), причем последний может быть положительным (если тепло выделяется) и отрицательным (если тепло поглощается). Величина теплового эффекта зависит от термодинамических эквивалентов всех тел, участвующих в реакции: она есть разность между суммой термодинамических эквивалентов веществ, образующих соединение, и термодинамических эквивалентов образовавшегося соединения, или

где w – тепловой эффект, x’, x”, x”’ etc. – термодинамические эквиваленты составных тел, а r – соединения. Нетрудно видеть, что из высказанного положения, основанного на законе сохранения энергии, вытекает, как следствие, закон Гесса.

Ю. Томсен предложил следующие обозначения для выражения результатов термохимических исследований. Тепловой эффект, происходящий при образовании какого-либо соединения X_a Y_b Z_c из его составляющих aX, bY и cZ, он изображает так:

Таким образом (Pb, S, О₄) изобразит тепловой эффект при образовании сернокислого свинца из свинца, серы и кислорода; (PbS, О₄) (PbO, SO₃) и т. д. изобразят тепловой эффект перехода от сернистого свинца, окиси свинца к сернокислому и т. д. Термодинамический же эквивалент различных тел можно изобразить так же, заключая формулу тела в скобки; так, (Рb) (Pb NO₃), (PbSO₄) и т. д. изображают термодинамические эквиваленты свинца, азотнокислого свинца, сернокислого и т. д. Согласно формуле (I) можно написать:

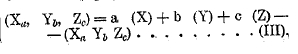
Если сумма термодинамических эквивалентов тел, входящих в соединение,  больше термодинамического эквивалента соединения, то последнее происходит с выделением тепла, в противном случае наблюдается поглощение тепла. Прибавим к этому, что все величины Ю. Томсен относит к грамм-эквиваленту тел.

В 1865 г. появилась первая работа М. Бертло: «Recherches de Thermochimie. 1-er Mémoire, etc.», и затем в течение ряда десятилетий продолжались работы этого ученого, обогатившего термохимию множеством новых фактов, методов и законностей (см. ниже).

Из германских ученых укажем на Штомана (Stohmatm, 1832—1897), подвергшего систематическому  исследованию теплоты сгорания органических соединений и различного рода пищевых тел.

Из русских ученых, работавших в этой области, можно указать академика Н. Н. Бекетова, В. Ф. Лугинина, Е. В. Вернера, И. М. Чельцова, Н. Д. Хрущова, И. А. Каблукова, И. В. Зубова, В. В. Свентославского, А. И. Щукарева и др.

Теоретические и опытные исследования Н. Н. Бекетова в области термохимии начались еще в 50-х годах XIX ст. Им тогда еще было указано, что количество тепла, выделяемое при соединении данных простых тел, не может служить мерою их сродства, а представляет разность между сродствами однородных и разнородных атомов.

В. Ф. Лугининым произведена масса опытных определений теплот испарения тел, нейтрализации, горения органических тел и т. п., причем им разработаны и усовершенствованы многие методы калориметрических измерений.

Термохимические обозначения. Выше мы видели как Ю. Томсен предложил выражать результаты термохимических исследований. В. Оствальд предложил для этой цели другие обозначения. Количество тепла, выделяющегося при образовании какого-либо химического соединения, показывает, насколько меньше запас потенциальной химической энергии (по Ю. Томсену, термодинамический эквивалент) сложного тела (выраженный в тепловых единицах), сравнительно с запасом ее в элементах. Мы не можем знать всего запаса химической энергии, находящегося в элементах, т. е. нам неизвестно, какое бы количество тепла мы получили, если бы всю химическую энергию данного элемента превратили в теплоту. Мы можем измерить только изменение запаса энергии при образовании сложного тела.

Большинство сложных тел образуется из элементов с выделением тепла; в них запас химической энергии меньше, чем в элементах. Реакции, при которых они образуются, называются экзотермическими. Но существуют сложные тела, — например, закись азота, циан, — при образовании которых тепло поглощается. При реакции их образования, теплота превращается в химическую энергию, и такие сложные тела обладают большим запасом энергии, чем элементы их составляющие. Реакции, при которых поглощается тепло, называются эндотермическими.

Результаты термохимических исследований можно выразить уравнениями, аналогичными тем, какими выражаются химические реакции. Можно условиться выражать химическим знаком элемента не только его атомный вес, но и запас химической энергии, заключающийся в 1 грамм-атоме элемента. Химическая же формула соединения будет обозначать не только его состав, но и запас энергии в 1-ой грамм-молекуле. Например, уравнение Н₂ + О = Н₂О + 69 К. показывает, что в 2,016 г водорода и 16 г кислорода содержится количество химической энергии более, чем в 18,016 г воды на количество, эквивалентное 69 большим калориям (К).

Уравнение Pb + 2J = PbJ₂ + 39,8 К. означает,  что 206,9 г свинца и 253,8 г йода образуют 460,7 г йодистого свинца, причем выделяется 39,8 К., или же, что запас химической энергии в 206,9 г свинца и 253,8 г йода превышает запас энергии в 460,7 г йодистого свинца на количество, эквивалентное 39,8 К. Эти уравнения количеств энергии позволяют производить с ними те же операции, какие производятся с алгебраическими уравнениями. Так, уравнение Hg + О — HgO = 21,5 К. показывает, что разность между количествами химической энергии в свободных ртути и кислороде и в окиси ртути эквивалентна 21,5 К.

Уравнение HgO = Hg + О — 21,5 К. показывает, что при разложении окиси ртути (216 г) нартуть (200гр.) и кислород (16 г) поглощается 21,5 К. Основываясь на законе Гесса, можно, с помощью подобного рода уравнений, легко вычислить тепло, выделяющееся при таких реакциях, которые недоступны непосредственному калориметрическому определению.

І-й  пример. Теплота образования окиси углерода из угля (аморфного) и кислорода вычисляется на основании теплоты образования углекислоты из угля и кислорода и теплоты сгорания окиси углерода:

Вычитая второе уравнение из первого, получаем:

т. е. при образовании окиси углерода из аморфного углерода и кислорода выделяется 29,35 К.

II-ой пример. Прямое определение количества тепла, выделяющегося при переходе аморфного угля в алмаз и графит, невозможно; основываясь же на том, что:

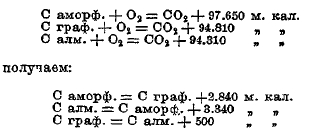
III-ий пример. Теплота образования органических соединений вычисляется на основании теплоты их горения; например, теплота горения метана, по Бертло, равна 218,5 К.; отсюда:

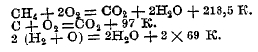
Вычитая из первого уравнения второе и третье, получаем:

т. е. теплота образования грамм-молекулы метана из аморфного угля и водорода равна 21,5 К.

Методы термохимических измерений см. калориметрия.

Зависимость теплоты реакций от температуры может быть выведена на основании закона сохранения энергии. Пусть Q₀ обозначает тепловой эффект какой-либо реакции при температуре t₀, а Q₁ то же при t₁, ∑с₀ — сумма молекулярных теплоемкостей исходных тел, ∑с₁ — то же продуктов реакции. Представим следующий круговой процесс, при коем система, претерпев ряд изменений, возвращается к начальному состоянию, так что сумма всех тепловых (выделенных и поглощенных) эффектов будет равна нулю: (1) реакция совершается при t₀, причем выделяется (2) продукты реакции нагреваются от t₀ до t₁, при этом поглощается тепло, равное (t₁ — t₀) ∑с₁ (3) при t₁ реакция идет в обратном направлении, причем поглощается количество тепла Q₁; (4) первоначальные тела охлаждаются от t₁ до t₀, причем выделится (t₁ — t₀) ∑с₀. Принимая выделившиеся количества тепла положительными, а поглощенные — отрицательными, мы можем написать следующее уравнение:

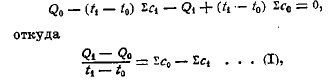
т. е. увеличение теплового эффекта при повышении температуры на один градус равняется разности между теплоемкостью тел реагирующих и таковой продуктов реакции.

Если молекулярные теплоемкости (∑с₀ и ∑с₁) будут равны между собой, тепловой эффект не будет изменяться с температурой. При реакциях между твердыми телами, а также жидкими растворами, тепловой эффект изменится с температурой незначительно, так как ∑с₀ и ∑с₁ или равны между собой, или приближаются друг к другу.

Так как зависимость теплоемкости тел от температуры выражается формулой: с_t = с₀ + at + bt² +…, то, вставляя подобное выражение в уравнение (I), получаем:

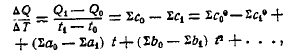
т. е. зависимость теплового эффекта от температуры может быть выражена:

где α, β могут быть вычислены на основании коэффициентов a₀, b₀, a₁, b₁ и т. д. Формула (II) служит в том случае, если реакции, совершаемые при разных температурах, относятся к одному и тому же агрегатному состоянию тел. Если же при переходе от одной температуры к другой состояние тел изменяется, то кроме теплоемкостей (∑с) нужно принять во внимание теплоту плавления, испарения и т. д.

Теплоты, реакций при постоянном давлении и постоянном объеме являются неодинаковыми. Если при реакции происходит увеличение объема, равное Δv, а внешнее давление равно Р, то происходящая при этом работа равна Р.Δv. Если при реакции объем увеличивается (Δv — положительно), то система производит внешнюю работу, на которую затрачивается тепло, и теплота реакции при постоянном объеме будет больше таковой при постоянном давлении; в том же случае, когда происходит сжатие (Δv — отрицательно), наблюдается обратное явление —  теплота реакции при постоянном давлении больше таковой при постоянном объеме. Если при реакции выделяется одна грамм-молекула газа (например, при действии серной кислоты на цинк), то при этом выделяющийся газ производит внешнюю работу Р.v, эквивалентную 1,98 Т малым калориям (см. далее).

Теплота растворения. При растворении различных тел в каком-либо растворителе, например воде, происходит поглощение или выделение тепла, величина коего зависит как от природы растворяемого тела, так и от количества растворителя и от температуры. При растворении какого-либо тела в постепенно увеличивающемся количестве растворителя, тепловой эффект все более и более приближается к известному пределу, так что дальнейшее прибавление воды к разведенным растворам не сопровождается измеримым тепловым эффектом. Обыкновенно это наблюдается, когда на 1 грамм-молекулу растворенного тела приходится 200, 300 и более молей (грамм-молекул) воды. Под теплотой растворения понимают количество тепла, поглощающееся или выделяющееся при растворении 1 моля тела в таком его количестве, что дальнейшее его прибавление не сопровождается измеримым тепловым эффектом. Такое количество воды Ю. Томсен обозначает значком Aq. Большинство определений теплоты растворения относится к температуре 18°С.

Растворение газов в воде во многих случаях бывает настолько мало, что тепловой эффект при этом не может быть измерен вследствие его незначительности. Но для некоторых он был измерен, и в следующей таблице помещены данные Ю. Томсена. При растворении газа в воде совершается отрицательная внешняя работа, так как происходит уменьшение объема системы; эта работа для одного моля газа равна 580 малых калорий, а поэтому это число нужно отнять из данных  таблицы, если желают знать теплоту растворения.

Теплота растворения газа в воде.

Пои  растворении в воде жидкостей наблюдается также выделение различных количеств тепла. Наиболее значительное количество тепла выделяется при растворении серной и пиросерной кислот. По Ю. Томсену, для серной кислоты:

для азотной кислоты:

для соляной кислоты:

При растворении твердых тел наблюдается во многих случаях отрицательный тепловой эффект (или поглощение тепла); в некоторых случаях происходит значительное выделение тепла, — например, при растворении KOH, CuSO₄ и т. п. соединении. Такое различное отношение к воде легко объясняется: при растворении твердого тела в воде происходит его превращение в жидкое состояние, а это превращение сопровождается поглощением тепла; если затем химическое взаимодействие между растворяемым телом и водой сопровождается выделением тепла, то последнее может быть менее теплоты плавления твердого тела, и поэтому тепловой эффект при растворении будет отрицательным.

Тепловой эффект Q может быть представлен в виде:

Q = — S + q,

где S — теплота плавления твердого тела, а q — тепло, выделяющееся при химическом взаимодействии растворенного тела и растворителя. Если q < S, Q — отрицательно, если же q > S, Q — положительно, т. е. происходит выделение тепла.

Последнее наблюдается при растворении многих безводных солей, которые способны образовать гидраты, — например, СuSO₄ и мн. других:

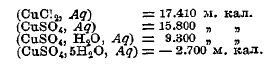
Поглощение тепла вообще наблюдается при растворении тел, не образующих с водой гидратов, например:

Ю. Томсен делит исследованные им соли на две группы: к первой принадлежат такие соли, теплота растворения и разведения которых положительна, ко второй — такие, для которых она отрицательна. Первую группу составляют — безводные азотнокислые соли: Mg(NO₃)₂, Mn(NO₃)₂, Zn(NO₃)₂, Cu(NO₃)₂; сернокислые: MgSO₄, MnSO₄, ZnSO₄ и CuSO₄; хлористые: CaCl₂, MgCl₂, ZnCl₂, NiCl₂, CuCl₂ и др.

Ко второй группе принадлежат: NaCI, NH₄CI, KBr, KCl, NaNO₃, NH₄NO₃, Sr(NO₃)₂, Pb(NO₃)₂ и др.

На основании закона Гесса теплота гидратации соли равна разности между теплотой растворения безводной соли и теплотой растворения ее кристаллогидрата, например:

Откуда теплота гидратации (SrC_l2, 6H₂О) = 18 640 малых кал.

Теплота гидратации представляет сумму двух величин: во-первых, теплоты превращения жидкой воды в твердую (или теплоты плавления с обратным знаком) и, во-вторых, теплоты, выделяемой вследствие химического соединения воды и соли. Первая величина известна: она равна 1 440 малых калорий для 1 моля воды. Следовательно, теплота соединения SrCl₂ с 6Н₂О (тверд.) = 18 640 — 6 Х 1 440 = 10 000 малых кал.

Теплота гидратации различных солей очень различна: она зависит как от природы соли, так и от числа присоединяемых молекул воды. Известно, что многие соли образуют несколько кристаллогидратов, например: CuSO₄, Н₂О и CuSO₄, 5Н₂О; Na₂SО₄, 7Н₂О и Na₂SO₄, 10Н₂О и т. п.

Теплота нейтрализации. Теплотой нейтрализации называют то количество тепла, которое выделяется при нейтрализации кислоты эквивалентным количеством основания.

Если мы будем к крепкому раствору кислоты приливать такой же раствор щелочи то тепловой эффект, наблюдаемый при этом, будет представлять собой сумму многих величин: кроме теплоты нейтрализации, в него будут входить теплоты разведения кислоты и щелочи, а эти последние очень разнообразны и завысят от природы как кислоты, так и основания. Поэтому для того, чтобы получить сравнимые результаты при нейтрализации разных кислот Ю. Томсен брал настолько разведенные растворы (на 1 мол. кислоты и основания 100 и более мол. воды), что при разбавлении их не получалось заметного теплового эффекта.

Главнейшие результаты, к которым пришел Ю. Томсен, следующие. Одноосновные кислоты показывают наиболее простое отношение при нейтрализации: теплота нейтрализации растет пропорционально количеству едкого натра, пока последнее не достигнет 1 моля на 1 моль кислоты, далее не наблюдается заметного теплового эффекта. (Только при фторнето-водородной кислоте происходит, вследствие действия фтористого водорода на образовавшийся фтористый натрий, заметное поглощение тепла). Для большинства кислот теплота нейтрализации 1 мол. едкого натра приблизительно одинакова: для 17 из 21 им исследованных одноосновных кислот (HNО₃, НСl, HJ, НВr, НРO₃ и др.) в среднем она равна 13 610 малых кал.; для фтористого водорода теплота нейтрализации самая большая: 16 270 малых кал.; для хлорноватистой кислоты, сернистого водорода и цианистого водорода она, напротив, значительно меньше: 9 980, 7 740, 2 770 малых кал.

Двухосновные кислоты по отношению к тепловому эффекту, который наблюдается при нейтрализации первой и второй молекулы едкого натра, могут быть разделены на три группы: 1) платинохлороводородная H₂PtCl₆ и кремнефтороводородная кислота у которых тепловой эффект для первой и второй молекулы едкого натра один и тот же (в среднем 13 500 малых кал.); 2) серная, селеновая, щавелевая и винная кислота, при нейтрализации которых первая молекула едкого натра вызывает меньшее выделение тепла, чем вторая. При нейтрализации серной кислоты первой молекулой едкого натра выделяется 14 750, а второй — 16 630 малых кал.; 3) сернистая, селенистая, углекислая и борная кислота. При этих кислотах первая молекула едкого натра дает больший тепловой эффект, чем вторая. Разница колеблется между 1 850 и 2 770 кал. При сернистой кислоте первая молекула натра выделяет 15 870, вторая — 3 100 малых кал.

Теория электролитической диссоциации легко объясняет, почему при нейтрализации различных одноосновных кислот выделяется одно и то же количество тепла (около 13 500 малых кал.) на 1 моль едкого кали. В разведенных растворах сильных кислот (HNО₃, НСl и др.) находятся главным образом ионы водорода (Н⁺) и (NO3^-) или (Сl^-), а в растворах едкого кали или натра находятся: (K⁺) или (Na⁺) и (ОН^-). При смешении же растворов едкого кали и соляной кислоты ионы калия (K⁺) и хлора (Сl^-), так ими и остаются, ибо степень диссоциации образующейся из них соли близка к таковой кислоты и основания, а катион (Н⁺) и анион (ОН^-) образуют молекулу (Н₂О). Уравнение реакции можно изобразить так:

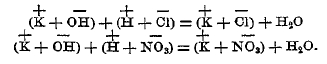
Таким образом, в обоих случаях образуется только молекула воды, и 13,5 больших калорий представляют теплоту образования молекулы воды из (Н⁺) и (ОН^-). Это же  число получается на основании измерений электропроводности воды при различных температурах (Кольрауш и Гейдвейлер).

Теплота образования солей из безводных, кислот и основания (например, едкого кали KОН) определяется на основании теплот нейтрализации кислот в растворенном состоянии и теплот растворения кислот, основания и образовавшейся соли. Покажем, как вычисляется теплота образования безводного уксуснокислого калия из жидкой уксусной кислоты (С2Н4О2) и твердого едкого кали (KОН). Имеем следующие уравнения:

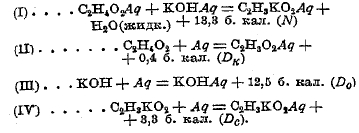
Сложив (I), (II), (Ш) уравнения, вычтя (IV) уравнение и сделав необходимые сокращения, получаем:

Если мы обозначим через N — теплоту нейтрализации, а теплоты растворения кислоты через D_K, основания — через D₀, ее соли — через D_c то, на основании уравнения (V), получаем:

где S — теплота образования твердой соли из жидкой кислоты и твердого основания, причем выделяется жидкая вода (см. уравн. I).

Чтобы узнать теплоту образования соли из твердой кислоты и твердого основания, нужно отнять теплоту плавления твердой кислоты.

При реакциях с такими кислотами, как НСІ, для которых неизвестны теплоты ни плавления, ни парообразования, ни удельная теплоемкость как в твердом, так и в жидком состоянии, рассчитывают теплоту образования соли, принимая кислоту и воду в газообразном состоянии. Для этого нужно к теплоте образования соли в твердом состоянии (N + D₀ — D_с) прибавить разность между теплотой растворения НСl (+17,4К.) и теплотой испарения воды при 15° (+10,7К.). Согласно с этим, имеем для

хлористых солей: S = N + D₀ — D_с + 6,7 больших калорий

бромистых солей: S = N + D₀ — D_с + 9,3 больших калорий

йодистых солей: S = N + D₀ — D_с + 8,9 больших калорий

фтористых солей: S = N + D₀ — D_с + 1,1 больших калорий

Когда у кислоты термические данные известны лишь для ее жидкого состояния, то теплоту образования соли в твердом состоянии рассчитывают, исходя из жидкой кислоты и жидкой воды. Это значит, что к теплоте нейтрализации необходимо прибавить теплоту растворения жидкой кислоты:

С помощью термических измерений можно разрешать вопросы, касающиеся строения химических соединений. Исследование двойных и комплексных солей (см. SVIII, 49/51) калориметрическим путем показывает, что двойные соли, — например, карналлит (KСІ.MgCl₂.6Н₂O) или квасцы, — в водном растворе не существуют, а находятся в разложенном состоянии. Двойная соль образуется только при кристаллизации. Например, в водном растворе карналлита находятся в отдельности KСІ и MgCl₂ (большею частью в виде ионов), при выпаривании же раствора при известных условиях выделяются кристаллы карналлита. Опыт показывает, что при смешении эквивалентных растворов хлористого калия и хлористого магния не происходит ни выделения, ни поглощения тепла. Если же мы смешаем раствор цианистого калия и цианистой ртути, то выделяется тепло:

В этом случае образуется комплексная соль, которая распадается на ионы:

Точно так же выделяется значительное количество тепла при образовании таких комплексных солей, как K₂PtCl₆, K₂PtBr₆ и т. п.

Теплота горения. Теплота горения какого-либо органического соединения представляет то количество тепла, которое выделяется, когда 1 моль (грамм-молекула) тела сгорает вполне, причем его углерод образует угольный ангидрид, водород — воду, сера — серный ангидрид, некоторые же элементы, каковы азот, галоиды, серебро, платина и т. п., выделяются в свободном состоянии. Такое полное горение происходит в калориметрической бомбе Бертло (см. калориметры), Малера и др. при избытке кислорода при давлении до 25 атмосфер, согласно уравнению:

Нужно различать теплоту горения при постоянном объеме Q_v и при постоянном давлении Q_p. Если при горении происходит изменение объема, то часть выделяющегося тепла идет на совершение внешней работы, требующейся для преодоления внешнего давления. Эта работа равна 1,98 Т малых калорий для каждой вновь образующейся грамм-молекулы газа (Т — температура по абсолютной шкале). На эту величину теплота горения при постоянном объеме будет превышать таковую при постоянном давлении, если происходит увеличение объема. Таким образом:

где n₁ — число молей газа, образующихся при горении, n₀ – число  молей газа, находившихся до горения.

Когда сжигаемое тело является жидким или твердым, то его объемом можно пренебречь, равно как и объемом образующейся воды, тогда

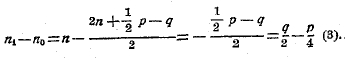
Когда сжигаемое вещество газообразно, то

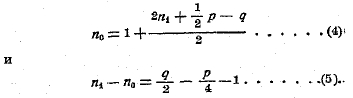
Для всех газообразных углеводородов (где q = 0) член (n₁ – n₀) в уравнении (2) есть величина отрицательная, т. е. теплота горения при постоянном давлении больше таковой при постоянном объеме. Например, при горении метана:

Если примем температуру опыта равной 20°С (Т = 293), то 2 х 1,98 Т = 1 161 малых калорий.

По Бертло, теплота горения метана при постоянном давлении — 213,5 больших кал., а при постоянном объеме — 214,4 больших кал., т. е. первая превышает вторую на 1 100 малых кал. Для кислородсодержащих органических соединений в большинстве случаев член (n₁ – n₀) отрицателен, но для целого ряда тел, состав коих выражается формулой С_nН_2mО_m, он равен нулю. К таким телам относятся углеводы. Для них объем образующегося угольного ангидрида равен объему потребляемого при горении кислорода.

При определении теплоты горения нужно всегда принимать во внимание, к какому состоянию тел она относится — к твердому, жидкому или газообразному, так как теплота горения в жидком или твердом состоянии будет отличаться от таковой в газообразном состоянии на теплоту плавления и испарения.

Изучение теллот горения составляло предмет исследования многих ученых (Ю. Томсена, М. Бертло, Штомана, В. Ф. Лугинина, В. В. Свентославского, П. В. Зубова и др.), и к настоящему времени (1928) мы обладаем громадным числовым материалом. Изобретение калориметрической бомбы Бертло позволило довести точность определения теплот сгорания до 0,1—0,2% (см. работы Л. В. Зубова). Весь этот громадный материал находится в справочниках, химических календарях и т. п. Укажем на некоторые законности:

1. Теплота горения гомологов углеводородов спиртов и кислот в газообразном состояния при постоянном давлении отличается на одну и ту же гомологическую разность, в среднем равную 158,6 больших кал., так что теплоты горения можно с достаточной степенью точности выразить уравнением такого вида:

Q = a + 158,6n,

где а — постоянная для каждого ряда, а n — число групп СН₂.

Первые члены рядов иногда немного отступают от этого, как это наблюдается и для других химических констант.

Для двухосновных кислот наблюдаются отклонения, указанные В. Ф. Лугининым.

2. Теплоты горения метамерных соединений, т. е. имеющих одинаковый состав, но различные химические функции, различны:

Альдегид СН.СНО  275,3 больших кал.

Окись этилена С₂Н₄О   302,3 больших кал.

Пропионовая кислота  366,9 больших кал.

Уксусно-этиловый эфир  895,3 больших кал.

3. Изомерные тела одинаковой химической функции обладают почти равными теплотами горения. Этот вывод, сделанный ранее, когда точность определения теплоты горения не была столь велика, как в последующее время, оказался не вполне верным: исследования П. В. Зубова, произведшего определения теплоты горения в калориметрической бомбе, с большой точностью показали, что изомеры не обладают вполне одинаковой теплотой горения. Например, теплота горения третичных спиртов менее таковой для вторичных и для первичных спиртов. И. А. Каблуковым еще в 1887 г. было указано, что этого нужно было ожидать.

Вышеуказанные и другие законности, наблюдаемые для теплот горения органических соединений, давно побуждали многих ученых отыскать общую формулу для вычисления теплоты горения органических соединений на основании их состава: такова, например, формула, предложенная французским ученым Лему и др. В 1922 г. акад. Д. И. Коновалов показал, что теплота горения органических соединений может быть вычислена по количеству кислорода, требующегося для полного сгорания данного соединения.

При калориметрических измерениях вода, образующаяся от сгорания, получается в жидком виде, и теплота ее сжижения прибавляется к теплоте сгорания. Теплотворная способность горючего материала выражается количеством единиц тепла, выделяемого при сгорании единицы веса горючего при условии, что вся вода остается в виде пара. Для отыскания теплотворной способности надо из найденной калориметрической величины вычесть скрытую теплоту испарения воды (круглым числом 600 малых калорий на 1 грамм воды). Теплотворная способность находится в зависимости от количества кислорода, требующегося для полного сгорания. Если мы назовем кислородным коэффициентом количество кислорода, расходуемого при сгорании 1 грамма горючего (обозначим его буквой К), то эта зависимость, по Д. Н. Коновалову, может быть представлена выражением

Р = 3 050 К (I),

т. е. количество тепла, развиваемого сгоранием при расходе 1 грамма кислорода, представляет постоянную величину 3 050 м калорий. Большое число органических веществ с точностью подчиняется этой формуле. Это уравнение представляет, таким образом, упрощенную форму более сложного закона и соответствует некоторому среднему, или нормальному, уровню теплотворных способностей органических тел.

Чистый аморфный углерод, в виде, например, древесного угля, развивает при полном сгорании на 12 граммов (атомный вес углерода) 97 600 малых кал. По формуле (I) мы найдем для 12 граммов 3 050 х 12 х 8/3 = 97 600 малых кал. Следовательно, веществами нормального уровня мы называем те, которые, сгорая, развивают на 1 г кислорода столько же тепла, сколько чистый древесный уголь. К таким веществам относятся, например, этан и его гомологи, нефть, этиловый спирт и др.

В приложении к определенным соединениям выраженная формулой (I) величина теплотворной способности (Р) для 1 грамма должна быть перечислена на молекулярный вес, а количество кислорода, израсходованного при полном сгорании, должно быть выражено числом его атомов (n), достаточным для полного сгорания частицы. Принимая во внимание, что тепловой эффект, выделяемый одним грамм-атомом кислорода, согласно формуле (I) должен составить 3 050 х 16 = 48 800 малых кал., находим молекулярную теплотворную способность Р:

Р = 48,800n (II),

где n — число атомов кислорода, необходимое для полного сгорания молекулы. По этой формуле мы находим теплотворную способность, например, этана С₂Н₆: Р=48 800 х 7 = 342 600, так как здесь n = 7 согласно равенству С₂Н₆ + 7O = 2СО₂ + ЗН₂О, а принимая воду, образовавшуюся при сгорании, в жидком состоянии и считая теплоту испарения воды на каждую частицу 10 600 малых кал., находим калориметрически определенную теплоту сгорания этана в больших калориях Q = 342,6 + 31,8 = 374,4 больших кал.; по прямому определению Бертло Q = 372,6 больших кал. Для этилового спирта С₂Н₆О n = 6, и по формуле (II) Q = 324,6; а по прямому измерению в калориметрической бомбе Q = 324,1.

Принимая во внимание, что отклонения от нормального уровня имеют место как вверх, так и вниз, формула (I) должна быть дополнена величинами, отвечающими этим отклонениям, и тогда мы имеем:

Р = 48 800n ± x (III).

Если х = 0, мы имеем вещества нормального уровня. Величины х, характеризующие отклонения от нормального уровня, Д. П. Коновалов называет термическими характеристиками соединений углерода. Для суждения о размерах и свойствах этих величин могут служить, прежде всего, данные для гомологических рядов. В гомологических рядах мы имеем ряды соединений одинаковых химических функций, с одной и той же во всех рядах разностью состава СН₂.

Гомологической разности состава СН₂ отвечает увеличение n на три (согласно равенству: СН₂ + 3O = СО₂ + Н₂О), а потому прирост величины теплотворной способности должен составлять: 48 800 x 3 = 146 400 малых кал., а прирост теплот сгорания Q = 146 400 + 10600 = 157 000. Опытные данные отвечают этой величине (см. выше). Если формулу (III) разделить на n, то мы получим:

p/n = 48,8 ± x/n.

Отсюда вывод: каждый гомологический ряд, какова бы ни была в нем величина х, по мере увеличения частицы приближается к нормальному уровню, для которого

p/n = 48 800 малых калорий

Наибольшее отклонение, если только оно свойственно ряду, мы найдем, поэтому, у первого члена ряда. Представители рядов, содержащие в частице всего один атом углерода, как метиловый спирт, муравьиная кислота, отклоняются от нормального уровня, и для них получаются следующие величины термической характеристики: для метана х = —3, для метилового спирта и для муравьиной кислоты х = 3. У всех прочих органических соединений х = 0 или х = ± 3S, где S — целое число, т. е. термические характеристики являются кратными трех.

Теплота образования органического соединения равняется разности между теплотой горения элементов, входящих в его состав, и теплотой горения самого соединения. Например, теплота образования углеводорода C_nH_2m равна

где f(C_nH_2m) означает теплоту горения при постоянном объеме. Зная, что

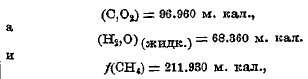
Получаем для теплоты образования

(СН₄) = 21 750 малых калорий.

Аналогичным образом могут быть вычислены теплоты образования всех органических соединений, теплота горения которых известна. Так, для некоторых углеводородов ароматического ряда, спиртов и альдегидов имеем:

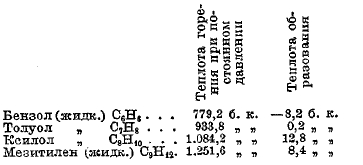
Данные таблицы показывают, что теплота образования органических соединений в сравнении с теплотой горения органических тел очень незначительна: для бензола она составляет 1% теплоты горения, а для ксилола и мезитилена около 1%. Вообще, по мере увеличения молекулярного веса углеводорода, теплота его образования составляет все меньшую и меньшую долю теплоты его горения.

То же самое наблюдается при других гомологических рядах: для метилового спирта теплота образования равняется почти 36% теплоты горения, для пропилового — около 16%, для бутилового — около 16%, а для амилового спирта — около 11%. Для бензойного альдегида теплота образования составляет менее 3%, а для коричного менее 1% теплоты горения. Таким образом, этот способ определения теплоты образования органических соединений приводит к результатам, не позволяющим делать какие-либо точные выводы относительно теплоты образования органических соединений. Все ошибки определения теплоты горения органических соединений, а также углерода и водорода, падают на теплоту образования, и хотя в настоящее время, как было выше указано, теплоты горения органических соединений определяются иной раз с точностью до 0,1%, но такие малые ошибки по отношению к теплоте образования будут составлять более 1%. Например, разность между теплотой горения изобутилового спирта и триметилкарбинола составляет 0,6%, а теплоты образования этих спиртов различаются более, чем на 4% друг от друга. Вот причины, почему долгое время не были подмечены разности в теплоте образования таких изомерных соединений, как первичные, вторичные, третичные спирты и др.

Измерения теплот сгорания послужили для суждения о строении органических соединении. Так, Ю. Томсен сделал попытку вычислить теплоту расщепления частицы углерода на отдельные атомы, а также теплоту присоединения водорода к углероду, теплоту образования простой, двойной и тройной связи и т. п. Не останавливаясь на изложении вычислений Ю. Томсена, приведем только некоторые его выводы.

1. Для того, чтобы произвести расщепление аморфного угля на атомы углерода в газообразном состоянии, нужно затратить на каждый грамм-атом 38,38 больших кал., а для алмаза 41,34 больших кал.

2. Теплота образования тройной связи v₃ = 0, двойной v₂ = 13,27 больших кал., а простой v₁ =  14,71 больших калорий.

Этими числами Ю. Томсен  пользуется для решения вопросов, касающихся строения различных органических соединений, например бензола. Он приходит к заключению, что в бензоле находится 9 простых связей.

Нужно иметь ввиду, что вычисления Ю. Томсена основаны на предположениях, которые не могут считаться бесспорными.

Как пример непосредственного измерения теплоты образования органических соединений можно привести определения теплоты присоединения брома к непредельным соединениям (исследование В. Ф. Лугинина и И. А. Каблукова), которая оказалась близка к 28 000 большим калориям.

Способ непрямого определения теплоты реакции. Развитие учения о химическом равновесии (см. ХІ/V, ч. 2, 332/40) указало способ определения теплоты реакции на основании константы равновесия K. Напишем общее уравнение реакции, ограниченное пределом:

Если обозначим через

концентрации тел

(число грамм-молекул в единице объема), установившиеся после того, как наступило химическое равновесие, то на основании закона действия масс для газообразной среды или разведенных растворов имеем:

где K — константа (постоянная) равновесия — величина для данной температуры определенная. С другой стороны, если рассматривать реакцию при постоянном объеме, то изменение величины K в зависимости от температуры определяется по формуле, выведенной Вант Гоффом:

где In —  натуральный (Неперов) логарифм, log — Бриггов логарифм (при основании 10), U — выделившееся тепло при абсолютной температуре Т. Это — так называемые уравнение изохоры.

В тех случаях, когда U не изменяется от температуры, интегрируя уравнение (2), получаем:

ln K = U/1,98T + J (3)

где l — постоянная интегрирования. Если известны значения K₁ и K₂ при Т₁ и Т₂, то на основании уравнения (3) получаем:

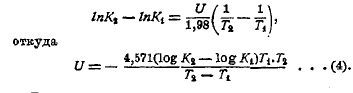
В тех случаях, когда U меняется с темпера турой незначительно, уравнение (4) позволяет вычислить U с приближением для средней температуры

(Т₂+Т₁)/2,

лежащей между Т₁ и Т₂, если последние отстоят недалеко друг от друга.

Примеры:

1. Для диссоциации серного ангидрида

Боденштейн и Поль нашли следующие константы равновесия:

Как показывает таблица, U постепенно увеличивается с температурой. Экстраполируя на основании этих чисел, для обыкновенной температуры получаем U = — 23 100, тогда как Бертло нашел — 22 600 кал.

2. Как показали исследования плотности пара элементов (например, галоидов), удельный вес их при повышении температуры понижается; так, для паров йода Мейер и Крафте (1880) нашли удельный вес по отношению к воздуху:

D = 8,74 при 448°С; D = 7,01 при 1 043°С; D = 5,06 при 1 468°С.

Это показывает, что при повышающейся температуре молекула йода распадается на атомы:

Процент разложенных молекул растет с температурой. Боденштейн вычислил, что теплота диссоциации молекул йода:

Для диссоциации же молекулы водорода Лангмюр нашел:

Н₂ = Н + Н — 98 000 малых калорий, при Т = 1 000 — 2 000°.

Пользуясь уравнением (4), можно вычислить теплоту диссоциации молекулы соли на ионы, теплоту превращения одной таутомерной (см.) формы в другую, теплоту растворения и т. п.

Закон наибольшей работы (Principe da travail maximum) и тепловая теорема Нернста. В 1875 г. М. Бертло формулировал следующее положение: Всякое химическое превращение, совершающееся без вмешательства посторонней энергии, стремится к произведению тела или системы тел, которые выделяют наибольшее количество тепла.

Закон наибольшей работы был в высшей степени плодотворен для разъяснения основных вопросов химической механики: во-первых, он вызвал массу исследований самого М. Бертло, направленных к его доказательству, во-вторых — возникла целая обширная литература из трудов самых выдающихся исследователей (например, Больтцмана, Дюгема, Гельмгольца, Вант-Гоффа, Горстмана, Нернста, Оствальда, Ратке), которые, основываясь отчасти на теоретических соображениях, отчасти на экспериментальных данных, показали, что закон этот имеет ограниченное значение. Для подтверждения своего закона М. Бертло произвел массу исследований, причем ему пришлось прибегать ко многим гипотетическим объяснениям наблюдаемых отступлений.

Согласно Лешателье, принцип наибольшей работы представляет первое, в высшей степени интересное приближение к общему закону, точная формулировка которого лежит в области учений об энергии, и хотя принцип наибольшей работы не имеет общего значения, но им можно руководствоваться, когда соблюдаются следующие условия: 1) реакция совершается при низкой температуре, приближающейся к абсолютному нулю; 2) реакция происходит между твердыми телами, причем продуктами ее являются тоже твердые тела.

Как это заметил Вант Гофф, обычные температуры, при которых протекают реакции, вообще мало отдалены от абсолютного нуля (на несколько сот градусов), так что принцип Бертло (наибольшей работы) пригоден в большинстве случаев, особенно, когда выделяется большое количество тепла. Но там, где температура измеряется большими десятками сотен или тысячами градусов (например, на солнце, где температура достигает 5 000° — 6 000°), реакции протекают обычно с поглощением тепла (эндотермические).

В вышедшей в 1897 г. «Thermochimie»   М. Бертло о законе наибольшей работы говорит только в первой главе, озаглавленной «Принцип наибольшей работы и энтропия». В заключение этой главы он указывает, что в реакциях между твердыми телами, как принцип наибольшей работы, так и принцип увеличения энтропии (см.) приводят к одним и тем же следствиям.   Но «в явлениях диссоциации (см.) энтропия играет существенную роль и вводит предвидения, которые ускользают отчасти от первоначальной формулировки закона наибольшей работы».

Д. И. Менделеев в своих «Основах химии», указав, что «принцип наибольшей работы не удержан наукой в его первоначальном виде», прибавляет, что «вероятно будет достигнут общий закон, какого в термохимии теперь не имеется».

Это предсказание сбылось в скором времени: в 1906 г. Нернст высказал свою тепловую теорему (которую также называют третьим законом термодинамики; ср. теплота), одним из частных следствий коей является принцип наибольшей работы.

Последняя четверть XIX столетия ознаменовалась развитием и проникновением в смысл второго закона термодинамики и приложением его выводов к учению о химическом сродстве. Немецкий ученый Горстман в 1875 г. первый показал, как, пользуясь принципом увеличения энтропии, можно вывести те законности, которые наблюдаются при явлениях диссоциации и других явлениях химического равновесия.

В 1882 г. Гельмгольц ввел понятие о свободной энергии. Он показал, что при химических явлениях, кроме той части химической энергии, которая превращается в какую-либо форму, способную сполна переходить в механическую работу (например, электрическую), необходимо отличать еще другую часть, переходящую только в тепловую энергию. Первую часть Гельмгольц предложил назвать свободной энергией, вторую — связанной.

Таким образом, если при химической реакции выделяется известный запас химической энергии (U), то часть его (А) может непосредственно перейти в механическую работу (или электрический ток), другая же часть (q) выделится при условиях реакции только в виде тепла:

где Q представляет количество тепла, эквивалентное изменению химической энергии.

Мы не можем судить о величине всей внутренней энергии (U) тела или системы тел, а можем измерять только относительные ее изменения: то же самое приходится повторить о свободной и связанной энергии. Уравнение (I) нужно, поэтому, прочесть так: изменение внутренней энергии тела (илы системы тел) равно сумме изменений его свободной и связанной энергии.

Бели какой-либо химический процесс происходит в калориметре, то выделенное тепло представляет общее уменьшение энергии в системе при таком необратимом процессе.

В том случае, когда тот же процесс происходит обратимым путем, например, в гальваническом элементе, то при этом совершается электрическая (или механическая) работа, равная уменьшению свободной энергии. Общее же уменьшение энергии (— U), происходящее при этом процессе, равно сумме свободной энергии (А) и связанной (q) (см. ур. I).

Гельмгольц указал, что свободную энергию можно рассматривать как работоспособность (Arbeitsfähigkeit) химических сил, связанную же - как скрытую теплоту. При постоянной температуре совершаются сами собой только такие процессы, при которых уменьшается свободная энергия (А), независимо от того, происходит ли при этом уменьшение или увеличение полной энергии.

В 1883 г. Вант Гофф предложил за меру химического сродства, проявляемого в данной реакции, принять максимальную работу, иными словами, свободную энергию, выделяющуюся при данном процессе.

На основании законов термодинамики Гельмгольц вывел следующее соотношение между изменением энергии (U) и свободной энергией:

т. е. разность между изменением всей энергии (U) и свободной (А) равна произведению абсолютной температуры на приращение свободной энергии (dA/dT), взятое с обратным знаком.

Из уравнения (II) видно, что А=U только в том случае, когда или T = 0 (т. е. реакция совершается при абсолютном нуле, или —273°С), или dA/dT = 0  (т. е. свободная энергия не меняется  с температурой).

Вообще же изменение свободной энергии (А) может или превышать изменение полной энергии (U) (когда dA/dT > 0, т. е. свободная энергия повышается с увеличением температуры), или быть меньше U (когда dA/dT < 0, т. е. с повышением температуры свободная энергия уменьшается).

Направление же химических процессов определяется величиной не теплового эффекта, а свободной энергии. Бели мы имеем уединенную систему тел, то в ней могут протекать только такие реакции, при которых свободная энергия всей системы уменьшается, а, следовательно, направление реакции определяется выделением наибольшего количества не тепла, а свободной энергии.

Принцип наибольшей работы, как указывал сам М. Бертло, оказывается верным при абсолютном нуле или температурах, близких к нему, когда тепловой эффект и свободная энергия реакции будут равны.

Для того, чтобы определить направление реакций данной системы, нужно уметь вычислить изменения ее свободной энергии. Из уравнения (II) имеем

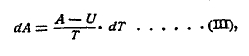
т. е., зная свободную энергию (А) и тепловой эффект (U) при одной температуре, можно вычислить изменение свободной энергии и таким образом определить ее при температуре, лежащей вблизи, и далее определить при всех последующих температурах.

Если U не меняется с температурою или зависимость ее от последней известна, то, согласно уравнению (III), можно вычислить А при всех температурах, но только в том случае, если мы знаем А хотя бы при какой-либо одной определенной температуре, так как, кроме уравнения, оба закона термодинамики не дают никаких указаний, как из теплового эффекта определить свободную энергию (А).

В 1906 г. Нернст указал, что, допустив нижеследующие предположения, можно вычислить свободную энергию А на основании термических данных.

1. При абсолютном нуле (т. е., когда Т = 0) свободная энергия (А₀) равна тепловому эффекту, иными словами, — изменению полной химической энергии U₀, т. е.

2. Не только при абсолютном нуле, но и при температурах, близких к нулю, разность между тепловым эффектом и свободной энергией равна нулю, т. е.

При этом нужно принять во внимание, что оба положения применимы только к твердым и жидким телам, ибо при абсолютном нуле газы не могут существовать.

Выше было указано, что зависимость теплового эффекта (U) от температуры (Т) может быть выражена уравнением

(см.   уравнение II), где U₀ — тепловой эффект при абсолютном нуле, а α, β, γ — постоянные, которые могут быть определены на основании измерения теплоемкости реагирующих тел при разных температурах. На основании уравнений (II) и (VI) можно придти к следующей окончательной формуле для U и А:

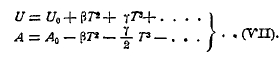
Таким образом, определив опытным путем постоянные β, γ...и измерив U при какой-либо температуре Т, мы можем из уравнения (VII) вычислить величину U₀, т. е. тепловой эффект при абсолютном нуле, далее, так как А₀ = U₀, то мы можем вычислить свободную энергию при всякой температуре.

Таким образом, задача определения свободной энергии на основании термохимических данных получает полное разрешение. Но для того, чтобы можно было пользоваться уравнениями (VI) и (VII) для экстраполяции и на основании их определять значения А₀ = U₀, необходимо, чтобы определения теплоемкости тел были произведены при температурах, по возможности близких к абсолютному нулю. Кроме того, одним из следствий теоремы Нернста был вывод, что теплоемкость тел при приближении к абсолютному нулю должна быстро падать и делаться ничтожно малой. Этот вывод получил опытное подтверждение в работах Нернста и его сотрудников над определением теплоемкости твердых тел при температуре жидкого водорода (около — 250°С).

«Было бы очень трудно, говорит Сванте Аррениус, показать обоснованность предположения, что dU/dT = 0, при приближении к Т = 0, так как невозможно делать определения при температуре абсолютного нуля. Но теория квант, которая сыграла такую большую роль в современном развитии физики, приводит к значениям:

Действительно, Эйнштейн доказал в 1907 г., что теплоемкость твердых тел должна быть равна 0 при абсолютном нуле (T=0). Если это правильно, то отсюда следует, что для этих тел (единственно существующих при Т=0)

Нернст, который еще в 1906 г. предполагал атомную теплоемкость равной 1,5 для всех элементов, тотчас понял значение вывода Эйнштейна и начал свои важные определения теплоемкостей при низких температурах, показавшие, что теплоемкость твердых тел сильно понижается при приближении к абсолютному нулю.

Теорема Нернста в сочетании с теорией квант привела к установлению взаимоотношений между большим количеством свойств, как то: температурой плавления, коэффициентом упругости и теплового расширения, электропроводностью металлов и т. п. Теорема Нернста может быть применена, строго говоря, к твердым и жидким телам, так как газы не существуют при температурах, близких к абсолютному нулю. Между тем реакции, в которых участвуют газообразные тела, имеют не только теоретический интерес, но и большое практическое значение. Поэтому естественно, что Нернст пожелал рассмотреть и эти случаи, которые очень трудны, так как газы не существуют при температурах, близких к абсолютному нулю. Он нашел, по характеристике С. Аррениуса, очень остроумные разрешения этого затруднения.

С. Аррениус указывает, что  теорема Нернста, верная по теории квант для реакций, которые происходят между кристаллическими веществами, не верна ни для растворов, ни для жидкостей, включая в число последних и аморфные, стеклообразные вещества, но, по-видимому, отклонения, обнаруживаемые аморфными телами, настолько малы, что возможно применять к ним «третье начало» с достаточным приближением. «С практической точки зрения нужно признать, что работы, которые были вызваны теоремой Нернста, были первостепенной важности для выяснения свойств тел при низких температурах и для приближенных вычислений химических равновесий при высоких температурах». (См. С. Аррениус, «Проблемы физической и космической химии», лекции, чит. в Сорбонне в 1922 г., Лнг., 1925).

Литература. М. Berthelot: 1) «Essai de mécanique chimique fondée sur la thermochimie», 2 vol., Р., 1879; 2) «Thermochimie, données et lois numériques», 2 vol., Р., 1897; 3) «Traité pratique de calorimétrie chimique», Р., s. а.; 4) «Chaleur animale. Principes chimiques de la production de la сhaleur chez les êtres vivants. I. Notions générales», Р., s. а.; «М. Бертло», изд. Всес. Акад. Наук, Лнг., 1927; Brion, «Thermochimie», Р., 1926: J. Thomsen, «Thermockemische Untersuchungen», 4 vol., Leipz., 1882—86; В. Ф. Лугинин, «Описание различных методов определения теплот горения органических соединений», М., 1894; В. Ф. Лугинин и А. Н. Щукарев, «Руководство к калориметрии», М., 1905; И. А. Каблуков, «Основные начала физической химии», вып. III, М., 1902; Н. Н. Бекетов, «Основные начала термохимии», 4 лекции, читанные в московском университете, в 1890 г.; W. Nernst, «Die theoretischen und experimentellen Grundlagen des neuen Wärmesatzes», 2 Aufl., 1924; F. Pollitzer, «Die Berechnung chemischer Affinitäten nach dem Nernst’schen Wärmetheorem», 1912; «Chemiker Kalender» von Dr. Biedermann, 1926 и сл. (в нем находятся таблицы термохимических данных); О. Sackur, «Lehrbuch der Thermochemie und Thermodynamik».

И. Каблуков.