Топология

Топология (или Analysis situs), часть геометрии, изучающая такие свойства фигур, которые сохраняются после любого взаимно однозначного и взаимно непрерывного преобразования фигуры. Наглядное представление о такого рода преобразованиях можно получить, вообразив фигуру, сделанную из легко деформируемого материала, например, из резины или мягкой глины; тогда всякое растяжение, сжатие и т. п. преобразование фигуры, при котором не происходит ни разрывов, ни слияния частей, ранее бывших разрозненными, будет некоторым взаимно однозначным и взаимно непрерывным преобразованием этой фигуры.

Точное определение взаимно однозначного и взаимно непрерывного преобразования некоторой фигуры А в фигуру В заключается в следующем: 1° каждая точка фиг. А переходит в одну, вполне определенную, точку фиг. В, причем в каждую точку фиг. В переходит одна и только одна точка фиг. А («взаимная однозначность»); 2° если х и у — произвольно заданная пара соответственных точек фиг. А и В, то каково бы ни было (сколь угодно малое) положительное число с, найдется такое (достаточно малое) положительное число η, что вое точки фиг. A, отстоящие от точки х на расстоянии меньшем, чем η, переходят в точки фиг. В, отстоящие от у на расстоянии меньшем, чем с, и, обратно, всем точкам фиг. В, удаленным от у меньше, чем на η, соответствуют в А точки, удаленные от х меньше, чем на с («взаимная непрерывность»).

Если выполнены условия 1° и 2°, то фигура В называется гомеоморфной фигуре А. Если В гомеоморфна А, то и обратно — А гомеоморфна В. Треугольник (совокупность его сторон) гомеоморфов окружности, но окружность не гомеоморфна отрезку прямой; шар гомеоморфен

цилиндру, но не гомеоморфен тору (рис. 1) и т. д. Установление критериев гомеоморфности фигур относится к числу наиболее важных и трудных задач Т.

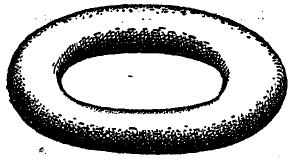
Рис. 1. Тор.

В настоящее время можно указать три основных отдела топологии.

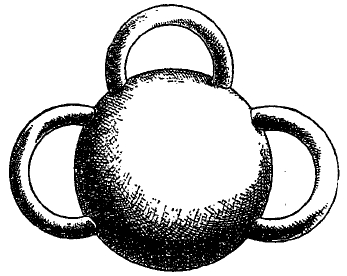
Рис. 2. Двусторонняя замкнутая поверхность рода 3.

I. Комбинаторная топология изучает, прежде всего, замкнутые многообразия, т. е. фигуры, составленные, по определенным законам, из конечного числа   т. н. симплексов или элементов; в одномерных многообразиях симплексами (элементами) являются прямолинейные (криволинейные) отрезки, в двумерных — прямолинейные (искривленные) треугольники, в трехмерных — прямолинейные (искривленные) трехгранные пирамиды и т. д.

Всякое одномерное замкнутое многообразие есть простая замкнутая линия, т. е. фигура, гомеоморфная окружности. Всякая плоская простая замкнутая линия разбивает плоскость на две области (теорема Jordan'а).

Род двусторонней замкнутой поверхности равен р, если эта поверхность гомеоморфна поверхности тела, состоящего из шара с р «ручками» (рас. 2); род поверхности шара есть нуль, поверхность тора имеет род 1 и т. д. Двусторонние замкнутые двумерные многообразия исчерпываются поверхностями конечного рода.

Кроме замкнутых многообразий, рассматриваются также открытые (состоящие из бесконечного числа симплексов) и многообразия с краями. Помимо двусторонних существуют также и односторонние многообразия. На рис. 3 дан пример односторонней поверхности с краем.

Для всякой поверхности рода о (например, для выпуклого многогранника) число вершин минус число ребер плюс число граней равно 2 (формула Euler'а). Различные обобщения этой формулы для многообразия любого числа измерений играют важную роль в комбинаторной топологии.

Помимо многообразий, в комбинаторной топологии рассматриваются весьма часто более общие совокупности симплексов — т. н. комплексы.

Изучение n-мерных комплексов (в частности многообразий) для n≥3 представляет очень большие трудности. Важное значение имеют здесь т. н. числа Betti; однако, как показал Н. Poincaré, два многообразия с одинаковыми числами Betti могут быть не гомеоморфными друг другу. Большой интерес представляют также вопросы о взаимном расположении фигур («зацепления» и т. п.).

II. Топология непрерывных отображений изучает свойства многообразий, рассматривая однозначные (в одну сторону) и непрерывные отображения одного многообразия на часть другого (или самого себя). Важную роль играет здесь т. н. степень отображения («Abbildungsgrad»). Этими методами была, например, впервые доказана инвариантность числа измерений, евклидовых пространств, т. е. невозможность гомеоморфизма n-мерного эвклидова пространства с какой бы то ни было частью эвклидова пространства низшего числа измерений (теорема Brouwer'а).

К этому же отделу относятся теория векторных полей и теория неподвижных точек непрерывных отображений. В качестве примера приведем еще следующую теорему Brouwer'а: всякое взаимно однозначное и взаимно непрерывное преобразование круга самого в себя сохраняет неподвижной, по крайней мере, одну точку.

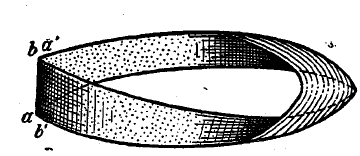
Рис. 3. Пояс Moebius’a. Получается из полосы abb’a’ приведением в совпадение b’a’ с ab (a’ попадает в b, b’ в a’).

III. Теоретико-множественная топология применяет в геометрии методы теории множеств (см. XLV, ч. 2, 27/28, и ХLI, ч. 7, 365'/69' и 451'/56'). Здесь изучаются наиболее общие геометрические образы — точечные множества. Надо отметить, прежде всего, понятие континуума. Континуумом в топологии называется всякое ограниченное замкнутое связное множество, отличное от одной точки (замкнутое множество называется связным, если оно не может быть разбито на два замкнутых подмножества без общих точек). Целый ряд свойств точечных множеств, лежащих в евклидовых пространствах, оказался зависящим лишь от немногих особенностей этих пространств. Это обстоятельство привело к рассмотрению более общих (абстрактных) пространств (ср. XLI, ч. 7, 409'/10'). Здесь надо отметить весьма плодотворные концепции топологического пространства и пространства метрического. Под топологическим пространством понимается абстрактное множество элементов («точек»), для каждого из которых определены «окрестности», удовлетворяющие т. н. четырем аксиомам Hausdorff’а. Если же оказывается возможным ввести для любой пары «точек»-«расстояние», удовлетворяющее трем аксиомам Fréchet, то пространство называется метрическим. Вопросы об установлении критериев метризуемости пространств, — т. н. «проблемы метризации», — были разрешены П. С. Урысоном и П. С. Александровым, вообще создавшими ряд отделов в теоретико-множественной топологии.

Одним из наиболее крупных завоеваний теоретико-множественной топологии является теория размерности, основанная Brauwer'oм и созданная П. С. Урысоном и К. Menger'ом. Эта теория позволяет определить число измерений произвольного точечного множества и любого абстрактного пространства. Помимо принципиального значения, которое имеет выяснение таких основных понятий, как линия, поверхность и т. д., теория размерности дает ряд интересных предложений о свойствах геометрических образований того или иного числа измерений.

Сказанные выше отделы топологии не разграничены резко друг от друга. Так, например, П. С. Александровым в ряде работ была установлена связь между n-мерными точечными множествами и элементарными образами из комбинаторной топологии. Впервые о топологических свойствах фигур упоминает Leibnitz. Riemann обнаружил значение топологии для теории аналитических функций. Затем следует указать на Poincaré, работы которого являются фундаментальными для комбинаторной топологии Brouwer, весьма много сделавший в топологии, создал топологию непрерывных отображений, Fréchet ввел абстрактные пространства, Brower, П. С. Урысон и К. Menger создали теорию размерности. Приложения топологии имеют место в некоторых вопросах теории аналитических функций, алгебраической геометрии, теории функций действительного переменного, теории дифференциальных уравнений и др. частей математики, а также в некоторых вопросах небесной механики (Poincaré, Birkhoff). Топология  сравнительно недавно сложилась в самостоятельную дисциплину. Работы Poincaré относятся к концу XIX и к началу XX в., работы же Brouwer’а, Fréchet, Sсhoenfiiess’а, Hausdorff’а, Janiszewski, П. С. Урысона, П. С. Александрова, О. Veblen’а, Alexander’а Lefschetz’а, Birkhoff’а, K. Menger’а, Nielsen’а, Antometa, Н. Hopf’а и др. относятся к нашему столетию. Ряд проблем и применений топологии еще ждет своих исследователей.

Литература: v. Kerékjártó, В., «Vorlesungen über Topologie» (Berlin, 1923, в серии «Die Grundlagen der mathem.   Wissenschaften in Einzeldarstellungen»); Veblen., O., «Analysis Situs» (Cambridge, 1916, Part II, New-York, 1920); Hausdorff, F., «Grundzüge der Mengenlehre» (Leipzig, 1914, 2-ое изд. Berlin, 1927); Р. Urysohn, «Mémoire sur les multiplicités Cantoriennes», 1-re partie, Fundamenta Mathematicae, t.t. VII. VIII (Warszawa, 1925—26); Fréchet, М., «Les Espaces Abstraits», Paris, 1928. Укажем еще на выходящие вскоре книги по топологии: П. С. Александрова (в той же серии, что и книга v. Kerékjártó), Н. Hopf’a — там же.

Л. Тумаркин.