Тригонометрия

Тригонометрия, учение о решении треугольников; решить треугольник (см.) значит определить все его элементы (3 стороны и 3 угла) по заданным трем (независимым между собой). Тригонометрия  называется прямолинейной, если она рассматривает треугольники, образованные прямыми линями (на плоскости), — сферической, если рассматривает треугольники, образованные дугами больших кругов на сфере, — псевдосферической, если треугольники образованы геодезическими линиями на псевдосфере. В силу общего принципа сохранения геометрии на поверхности при ее изгибании, прямолинейная тригонометрия применима также к цилиндрам, конусам (с произвольной направляющей), вообще ко всем развертывающимся (на плоскость) поверхностям; сферическая — ко всем изгибаниям шара, т. е. ко всем поверхностям постоянной положительной кривизны; псевдосферическая — к поверхностям постоянной отрицательной кривизны. Так как неевклидова геометрия в конечной области осуществляется на поверхности постоянной кривизны, — положительной или отрицательной, — то тригонометрия псевдосферическая имеет место в геометрии Лобачевского, а тригонометрия сферическая — в геометрии Римана (см. XLI, ч. 7. прил. 351'/62').

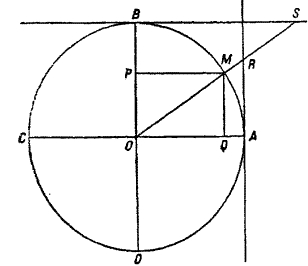
1. Основная задача тригонометрии – установить связь между сторонами и углами треугольника: при этом тригонометрия пользуется особыми, тригонометрическими функциями угла. Таких функций 6 – синус, косинус, тангенс, котангенс, секанс, косеканс. Тот отдел тригонометрии, который изучает их, называется гониометрией (измерение углов). В гониометрии рассматривают угол а = < АОМ (см. черт.) как центральный угол в круге (тригонометрический круг); при этом угол АОМ и дуга AM измеряются одним числом α. (Поэтому тригонометрические величины относятся безразлично к углу или дуге). Это число выражается или в градусах, или в абсолютной мере. В последнем случае за единицу принимается угол, дуга которого равна радиусу (180°/π = 57°17'44,8''). Если а — мера угла в градусах, а α — в абсолютной мере, то а = аπ/180°, где π = 3,14159... Дуга (и угол) отсчитывается от некоторой точки А (начало) на   окружности; при этом дуга (и угол) положительна, если откладывается в направлении против стрелки часов. Диаметр АС называется первым диаметром, перпендикулярный к нему BD — вторым. Они делят окружность на 4 четверти (первая, вторая и т. д.). Радиус ОМ, проведенный в конец М дуги, называется подвижным. Пользуясь этой терминологией, мы назовем линией синуса проекцию подвижного радиуса на второй диаметр ОР (или равный ей перпендикуляр на первый диаметр MQ); линией косинуса — проекцию подвижного радиуса на первый диаметр OQ; линией тангенса — отрезок касательной и окружности в начале А от точки касания до пересечения с продолженным подвижным радиусом АR; линией котангенса — отрезок такой же касательной в конце второго диаметра В от этой точки до пересечения с продолженным подвижным радиусом BS; линией секанса — отрезок продолженного подвижного радиуса от центра до пересечения с линией котангенса  OR; линией косеканса — такой же отрезок до пересечения с линией котангенса OS. Величиной синуса (косинуса и т. д.)  или просто синусом (косинусом и т. д.), называется взятое с определенным знаком отношение его линии к радиусу. Синус и тангенс считаются положительными, если отложены вверх; косинус и котангенс — направо; секанс и косеканс — в направлении подвижного радиуса (от точки О к точке М). Следовательно, в I четверти все 8 функций положительны; во II — все отрицательны, кроме синуса b косеканса, в III — кроме тангенса b котангенса; в IV — кроме косинуса и секанса.

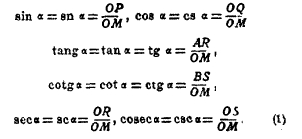
Из этого определения следует, что по абсолютной величине синус и косинус всегда меньше единицы, секанс и косеканс — больше единицы, тангенс и котангенс принимают все значения. Рассматривая дугу как путь, пройденный точкой, можно говорить о дуге, больше целой окружности. Увеличивая дугу на целое число окружностей, мы получим прежнюю точку М и, следовательно, те же 8 тригонометрических величин. Поэтому тригонометрические функции периодичны, т. е. не меняются от прибавления к аргументу (дуге) определенного числа (периода). Период тангенса и котангенса равен π (180°), всех остальных тригонометрических функций — 2π (360°). Так как каждая тригонометрическая функция определяет дугу, а, следовательно, и остальные функции, то между 6 тригонометрическими функциями одной дуги должно быть 5 (и только 5) независимых соотношений. Они получаются из чертежа (помощью теоремы Пифагора или из подобия треугольников):

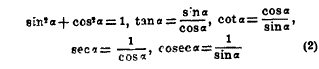
Из них как следствие, получаются новые:

Вторая группа формул определяет тригонометрические величины суммы (разности) дуг через тригонометрические функции слагаемых (теорема сложения):

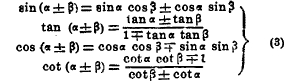
Прилагая последовательно эти формулы к равным дугам β=α получим формулы для кратных дуг:

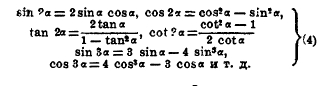
Подставляя вместо α дугу α/2, найдем формулы деления дуг:

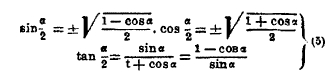
Выбор знака перед корнем зависит от того, в какой четверти лежит α/2.

Большое значение в практической тригонометрии имеют формулы, преобразующие сумму в произведение (приведение к логарифмическому виду)

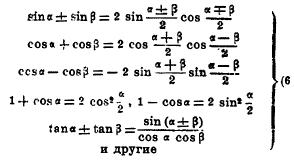
Для определения тригонометрических  величин существенно, что тригонометрическую функцию любой дуги можно выразить (формулы приведения) через функции дуги I четверти (и даже дуги меньше 45°). Сюда относятся, прежде всего, теоремы о тригонометрических функциях дополнительной дуги (угла). Так называется дуга (угол) π/2 – α = ^ ВМ, имеющая конец М, общий с датой α, а начало в конце второго диаметра В. Так как для нее второй диаметр BD является первым, и наоборот, то всякая тригонометрическая функция ее равна сопряженной функции основной дуги.

Sin(π/2 – α) = cos α, tan(π/2 – α) = cot α и т. д. (cosinus есть сокращенно complementi sinus). То же правило распространяется на дуги вида π/2 + α, 3π/2 ± α и т. д. (у концов второго диаметра ВD). Так как эти дуги оканчиваются не в первой четверти, то тригонометрические функции их могут быть отрицательны, и тогда формула должна иметь знак минус в правой части. Для дуг вида π±α, 2 π±α и т. д. (у концов первого диаметра АС) формулы приведения пишутся так же, но всякая функция переходит в ту же функцию основного угла. Например:

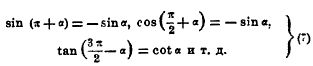
Обратными круговыми функциями называются арксинус (дуга данного синуса), арккосинус и т. д. Если у = sin х, то х = arcsin y; если  у = tan x, то х = arctan у и т. д. Так как каждому значению тригонометрической величины соответствует бесчисленное множество дуг (две дуги в пределах одной окружности, плюс сколько угодно периодов), то обратные круговые функции многозначны. Если х одно значение функции, то система всех значений определяется формулами:

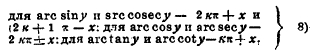
где k означает любое цело в число.

Лишь немногие дуги, соизмеримые с окружностью, имеют тригонометрические функции, выражаемые рациональным числом или простым радикалом. Таковы, например:

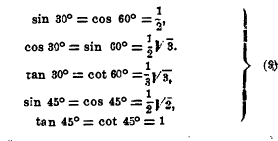
Тригонометрические функции других дуг вычисляются только приближенно. Для этой цели могут служить неравенства.

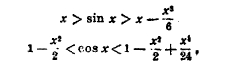
которые являются первыми членами бесконечных рядов (см. ХХII, 327/28, прил. 12, и ХII, 82):

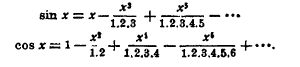
Вычисленные значения тригонометрических функций составляют таблицы тригонометрических величин. Обычно таблицы содержат логарифмы синуса, косинуса, тангенса и котангенса для дуг от 0° до 45°, через одну минуту, если таблицы вычислены с 5 знаками, и через 10”, если с 7 знаками.

2. Собственно тригонометрия (прямолинейная) прилагает тригонометрические функции к решению (прямолинейных) треугольников. Так как треугольник определен, если даны три его элемента (признаки равенства треугольников), то между 6 элементами треугольника должно существовать 3 независимых между собой соотношения. Одно из них известно уже из геометрии (сумма углов равна 180°), два других дает тригонометрия.

Задача значительно упрощается, если один из углов треугольника прямой (прямоугольный треугольник). Необходимые соотношения сейчас же следуют из определения тригонометрических величин (1), если рассмотреть прямоугольный треугольник OQM или OAR (см черт.). Их можно формулировать так:

катет равен гипотенузе, умноженной на синус противолежащего или косинус прилежащего (катету) угла;

катет равен другому катету, умноженному на тангенс противолежащего (определяемому катету) угла или на котангенс прилежащего.

Любые два из этих соотношений можно считать за основные, остальные суть следствия их так же, как и теорема Пифагора. С помощью этих теорем легко решаются все основные (когда даны 2 основных элемента) случаи решения прямоугольного треугольника.

Для косоугольного (или безразлично тупоугольного) треугольника эти соотношения имеют другую форму. Обозначим через А, В, С — углы, а, b, c — соответствующие стороны (сторона а лежит против угла А, и т. д.), R — радиус описанного круга, r —радиус внешнего круга, 2р — периметр, s — площадь треугольника. Тогда первая группа основных соотношений напишется:

Здесь между основными элементами треугольника (a, b, c, A, B, C) два независимых соотношения. Вторая группа основных соотношений получается из формулы

если одновременно вместо а и А подставить b и В  вместо b и В подставить с и С и вместо с и С подставить а и А (круговая замена).

Среди 3, получаемых таким образом, равенств — 2 независимы и могут быть приняты за основные. Наконец, можно принять за основные 2 из трех, получаемых круговой заменой из уравнения

Каждая из этих групп достаточна для решения треугольника, но для удобства вычислений (с логарифмами) их приходится значительно преобразовать. Можно различить 4 основных случая решения косоугольного треугольника.

I. Даны два угла и сторона. Третий угол определяется из основного соотношения А + В + С = 180°, остальные стороны — с помощью формул (10).

II. Даны две стороны и угол между ними, например а, b и С. Образуя из отношений (10) производную пропорцию, получаем новую формулу (формулу тангенсов)

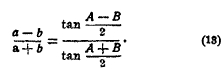
Здесь известно а, b и А + В = 180° — С: следовательно, найдем А — В, затем по сумме и разности А и В. Далее, как в I случае.

III. Даны две стороны и угол против одной из них, например а, b и А. Из формул (10) находим sin B = (b sin А)/a.  Задача невозможна, если b sin А > а; если b sin A = а, то B = 90°. Если sin А < a, то по синусу найдем два угла (В и 180° — В), если при этом b < а  то задача возможна и имеет одно решение (острый угол); если b > а,  то задача  возможна только при А остром и тогда имеет два решения. Далее, как в I случае.

IV. Даны три  стороны. Формулы (II) определят углы; для удобства логарифмирования их преобразуют в одну из трех форм:

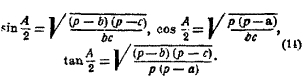
Для определения площади служат формулы:

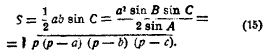
Радиус описанного круга R определяется по формуле (10) или еще

где P = 2p = a+b+c.

Для радиуса вписанного круга r имеем

Этими формулами можно пользоваться, если данные отличаются от основных (особые случаи). Кроме того, если даны сумма или разность двух сторон, то пригодны формулы Мольвейде:

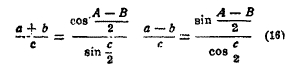
3. Сферическая тригонометрия рассматривает сферические треугольники. Так как с увеличением радиуса R сферы все размеры пропорционально увеличиваются, то формулы сферической тригонометрии содержат не длины сторон треугольника, а отношение стороны к радиусу шара, т. е. абсолютную меру дуги, которая образует сторону, или меру ее в градусах. Эту меру сторон мы обозначим буквами а, b, с; углы треугольника по-прежнему — А, В, С. При этом мы будем предполагать, что каждая сторона содержит меньше 180° (треугольники Эйлера). Сумма углов сферического треугольника более 180°; разность А+В+С—π = Е называется сферическим избытком: ER  есть площадь треугольника. Точки пересечения со сферой диаметра, перпендикулярного плоскости большого круга, называются его полюсами. Если мы установим определенное направление обхода сфер, треугольника и будем брать для каждой стороны треугольника ее, например, левый полюс, то мы получим новый сферический треугольник А’В’С’ полярно сопряженный данному. Стороны его дополняют углы основного треугольника до 180°, и наоборот: а' = π — А, а = π — А'. Этими формулами определяется полярное преобразование.

Сферический треугольник определен 3 элементами; значит, между его 6 элементами должно быть 3 независимых соотношения. Таковыми являются (теорема косинусов):

Cos a = cos b cos c + sib b sin c cos A (17)

Или полярная форма

Cos A = - cos B cos C + sin B sin C cos a (18)

Две другие формулы получаются круговой заменой. Отсюда следует (теорема синусов):

И ряд других более сложных соотношений.

Для решения прямоугольных треугольников А = 90° служат формулы.

Полярным преобразованием их служат треугольники со стороной а = 90°. Можно различить 6 основных случаев решения косоугольного сферического треугольника.

I и II. Даны 3 стороны или 3 угла. Можно пользоваться формулами (17) или (18). Лучше преобразовать их в форму

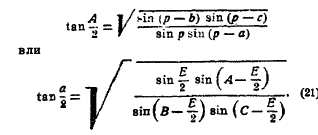
где 2p = a + b + с. Задача возможна, если р < 180° и а < b+c или если 0<E<360° и А >Е/2.

III и IV. Даны 2 стороны и угол между ними или 2 угла и сторона между ними.

Пользуемся формулами Непера:

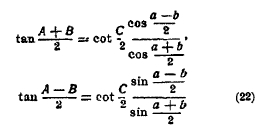
или полярно сопряженными. Задача всегда имеет единственное решение.

V и VI. Даны 2 стороны и угол против одной из них или 2 угла и сторона против одного из них. Снова пользуемся формулами Непера (22). Задача не всегда возможна и может иметь 2 решения.

Сферическая тригонометрия имеет большие приложения в астрономии, ради потребностей которой она и была построена значительно ранее прямолинейной тригонометрии (начатки уже у Птолемея, II век; см. ниже).

Псевдосферическая тригонометрия не имеет таких приложений. Вместе со сферической и прямолинейной она представляет единственно возможную тригонометрию, ибо только на поверхности постоянной кривизны треугольник вполне определен своими тремя элементами. Формулы псевдосферической тригонометрии выводятся из формул сферической тригонометрии таким простым замечанием.

Так как кривизна сферы 1/R’, а псевдосферы того же радиуса —1/R’ (см. XLI, ч. 7, прил. З60'/61') то радиус сферы R надо заменить на iR, где i =√—1. Радиус R входит в формулы сферической тригонометрии только посредством сторон, ибо a, b, c суть отношения длин сторон к радиусу сферы R. Следовательно, теперь а, b, с надо заменить на α/iR, β/iR, γ/iR, где α, β, γ – длины сторон; но согласно формулам Эйлера (см. XXII, 327/23 приложение 13).

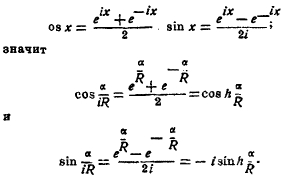
Эти функции (гиперболические) и надо подставить вместо прежних тригонометрических. Тогда, например, основные соотношения (17), (18), (19) примут вид:

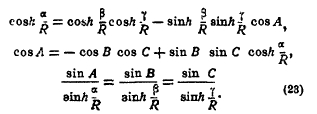
При этом следует иметь ввиду, что на псевдосфере одна или две и даже все три вершины треугольника могут лежать в бесконечности.

4. Первые сведения по тригонометрии встречаются уже в древнейшей математической рукописи — папирусе Rhind (1700—2000 лет до н. э.). Отношение Seqt есть, по-видимому, косинус угла наклона бокового ребра к плоскости основания пирамиды (обычно 52°). Предложения сферической тригонометрии («Begnla sex quantitatum») впервые высказаны в третьей книге сферик Менелая Александрийского (Рим, 98 г. н. э.). Он пользуется при этом, как и последующие авторы, вместо синуса понятием хорды двойной дуги. Первая таблица таких хорд, дающая возможность практического решения треугольников, дана Птолемеем Александрийским («Альмагест», 150 г.). Автор вычисляет хорды через каждые 30’ в 1/60 радиуса (τρήματα), минутах и секундах с точностью до 10^-6. Синус (как проекция дуги на диаметр) был введен в Индии под именем diyâ-ardha (половина хорды) астрономом Арьябхатта (родился в 476 г.). По сходству написания это название у арабских писателей приняло форму дшанб (по-арабски — грудь, сердце, сумка), буквальный перевод которого на латынь (Платон из Тиеоли, XII в.) есть sinus. В арабском Багдаде (Абуль-Вафа, 910—998) вводятся тангенс и котангенс, как две тени (umbra versa, umbra recta), секанс и косеканс — как их диаметры. Автору известны соотношения между этими величинами. Здесь же Насир Эддин (1201—1274) впервые излагает тригонометрию как самостоятельную дисциплину. В Риме тригонометрия осталась неизвестной. Первые переводы тригонометрии появились после завоевания Испании в Толедо в ХII в. («Альмагест» в 1175 г.). Только в XV в. Региомонтакус (1436—1473) построил всю тригонометрию синуса, исходя из обычного его определения; он же составил новую таблицу синусов через каждую минуту. Таблицы всех 6 тригонометрических функций в их современном расположении дал Ретикус (1514—1574). Развитие тригонометрических таблиц привело к использованию (протасферетический метод) теоремы сложения косинусов для замены умножения сложением. Виета (1540—603) систематически применяет все 6 тригонометрических функций к решению плоских и сферических треугольников. Виета, так же, как и Ретикус, отступил от названия sinus (perpendiculum), complementi sinus (basis) и т. д., уже в то время утвердившихся. Названия тангенс (вместо umbra recta) и секанс (вместо diameter umbrae) впервые появляются у Т. Финка. («Geometria rotundi», 1583). Сокращение cosinus вместо complementi sinus идет от Гунтера (1581—1626, Лондон). Изобретение логарифмов (Непер, 1614) было вызвано потребностью тригонометрии и повлекло развитие формул преобразования сумм в произведения, конец ХVII столетия характеризуется стремлением найти буквенную символику. Так, Яков Бернулли (1614—1705) пишет sin АС в смысле синус дуги АС. Создание анализа в ХVІI в. отразилось прежде всего в разложении тригонометрических функций в бесконечные степенные ряды (Hьютoн, 1666) и разложении синуса и косинуса кратных дуг (Муаер, 1667—1754). Производные тригонометрических функций впервые приводит Котес (1682—1716). В современный, знакомый нам вид привел тригонометрию Эйлер (1707—1783). Законченность символики (он пишет sin Z, cos Z), определение тригонометрических функций, как отношения; их периодичность; наконец, завершение сферической тригонометрии характеризуют работу Эйлера. Предпринятое в первые годы Великой революции гигантское предприятие издания Tables de Cadastre впервые провело вычисление тригонометрических величин при помощи бесконечных рядов и интерполяционных формул (натуральные синусы через 0,001.π/2 с 25 десятичными знаками; логарифмы через 0,00001.π/2 с 14 десятичными знаками). В XIX в. Кота вводит в тригонометрию метод проекций (1821). Мёбиус (1790—1888) распространяет сферическую тригонометрию на треугольники, стороны которых более полуокружности. Созданная Коши теория функции комплексного переменного дала новое обоснование тригонометрическим функциям, а развитие неевклидовых геометрии поставило новую проблему псевдосферической тригонометрии.

Литература. Кроме общей истории математики — Cantor М., «Vorlesungen über Geschichte der Mathematik», по истории тригонометрии можно указать — Dr. А. von Braunmühl. «Vorlesungen über Geechichte der Trigonometrie», 1900 и 1908. По прямолинейной и сферической тригонометрии см. Вебер и Вельштейн, «Энциклопедия элементарной математики», т. 3, кн. 2; по неевклидовой тригонометрии — Stäckel u. Engel, «Die Theorie der Рarallellmien von Euklid bis auf Gauss», 1895.

С. Фиников.